Круги Эйлера и их практическое применение

Содержание

1. Круги Эйлера и их практическое применение
2. Выполнила:Жубанова Диана ученица 7 классаКарасаевской СОШ
3. Цель исследования:Изучить круги ЭйлераНаучиться применять данный способ
4. Немного об историиЛеонард Эйлер, крупнейший математик XVIII
5. Немного об истории Но наибольшего
6. Применение простейших случаев кругов Эйлера - Венна
7. Применение простейших случаев кругов Эйлера - Венна
8. Применение простейших случаев кругов Эйлера - Венна
9. Задачи, решаемые с помощью кругов Эйлера - ВеннаЗадача
10. Задачи, решаемые с помощью кругов Эйлера - ВеннаЗадача №2.
11. Составление задач, имеющих практическое значениеЗадача
12. Составление задач, имеющих практическое значениеЗадача 3. 1)32-4=28(ч.)
13. Интеллектуальный марафон , заочный тур60
14. Ты человек, а значит, тыОбязан рассуждать –А
15. Алгоритм решения задач с помощью кругов Эйлера
16. Спасибо за внимание!!!
17. Скачать презентанцию

Выполнила:Жубанова Диана ученица 7 классаКарасаевской СОШ

Главная
Геометрия
Круги Эйлера и их практическое применение

Слайды и текст этой презентации

Слайд 1Круги Эйлера
и их практическое применение

Слайд 2Выполнила:

Жубанова Диана
ученица 7 класса
Карасаевской СОШ

Слайд 3Цель исследования:
Изучить круги Эйлера
Научиться применять данный способ для решения задач

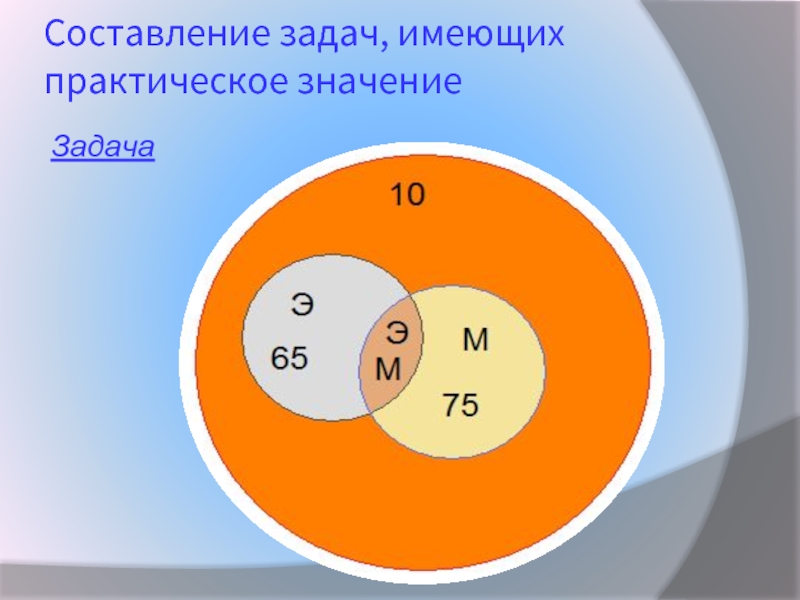
Cоставлять задачи практического содержания.
Задачи исследования:
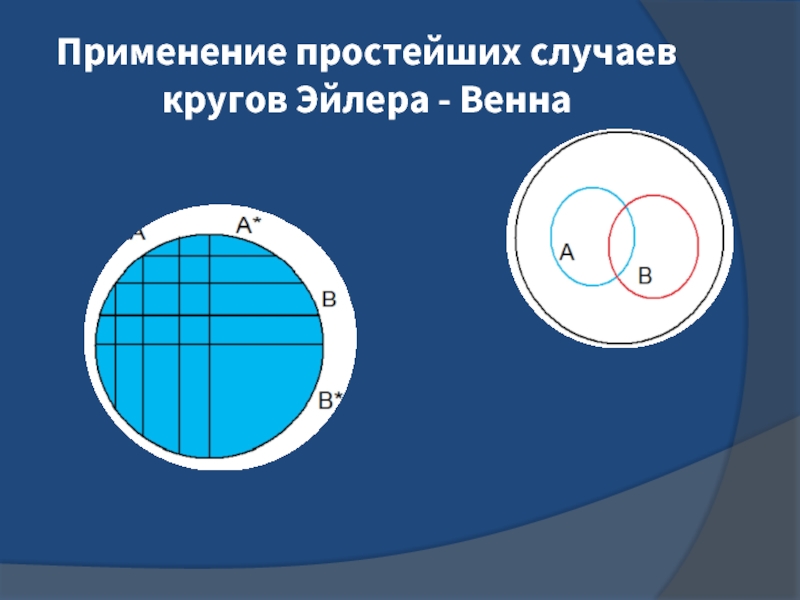
Познакомиться с кругами Эйлера, кругами (диаграммами)

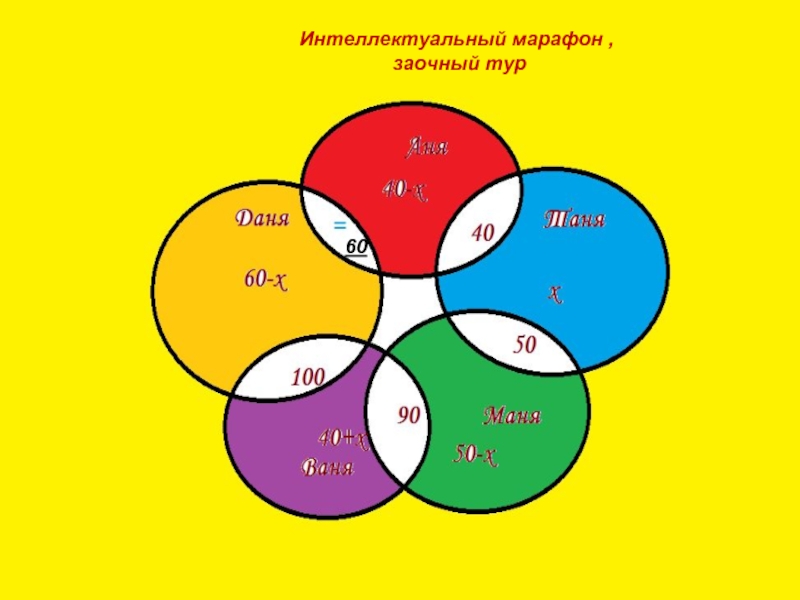
Эйлера – Венна.
Составлять и решать задачи с меняющимися данными условиями.
Проанализировать, как изменяется решение задачи при изменении части условия.

Цель исследования:Изучить круги ЭйлераНаучиться применять данный способ для решения задач Cоставлять задачи практического содержания.Задачи исследования:Познакомиться с кругами

Слайд 4Немного об истории
Леонард Эйлер, крупнейший математик XVIII века, родился в

Швейцарии. В 1727г. по приглашению Петербургской академии наук он приехал

в Россию. Эйлер попал в круг выдающихся математиков, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира.

Леонард Эйлер

Слайд 5Немного об истории
Но наибольшего расцвета графические методы

достигли в сочинениях английского логика Джона Венна (1843 – 1923).

С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.

Джон Венн

Немного об истории Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна

Слайд 6Применение простейших случаев кругов Эйлера - Венна

Слайд 7Применение простейших случаев кругов Эйлера - Венна

Слайд 8Применение простейших случаев кругов Эйлера - Венна

Слайд 9Задачи, решаемые с помощью кругов Эйлера - Венна
Задача

Слайд 10Задачи, решаемые с помощью кругов Эйлера - Венна
Задача №2.

Слайд 11Составление задач, имеющих практическое значение
Задача

Слайд 12Составление задач, имеющих практическое значение
Задача 3.
1)32-4=28(ч.) – играют хотя

бы в одну игру.
2)14-6-4-Х=4-Х (ч.) – играют только в баскетбол.
3)24-6-4-Х=14-Х

(ч.) – играют только в пионербол.
4)16-4-4-Х=8-Х (ч.) – играют только в волейбол.
5)4-Х+14-Х+8-Х+4+6+4=29 (ч.)
40-3Х=28
3Х=12
Х=4(ч.)

Составление задач, имеющих практическое значениеЗадача 3. 1)32-4=28(ч.) – играют хотя бы в одну игру.2)14-6-4-Х=4-Х (ч.) – играют

Слайд 13
Интеллектуальный марафон ,
заочный тур
60

Слайд 14Ты человек, а значит, ты
Обязан рассуждать –
А без логичной простоты
Ты

будешь пропадать.
Пусть за собой она зовёт –
Уйми в коленях дрожь!
Коль

с Логикой пойдёшь вперёд –
Нигде не пропадёшь!
(С. Алдошин)

Заключение

Ты человек, а значит, тыОбязан рассуждать –А без логичной простотыТы будешь пропадать.Пусть за собой она зовёт –Уйми

Слайд 15Алгоритм решения задач с помощью кругов Эйлера - Венна
Заключение
Записываем краткое

условие задачи.
Выполняем рисунок.
Записываем данные в круги (или в диаграмму Эйлера).
Выбираем

условие, которое содержит больше свойств.
Анализируем, рассуждаем, не забывая записывать результаты в части круга (диаграммы).
Записываем ответ.

Алгоритм решения задач с помощью кругов Эйлера - ВеннаЗаключениеЗаписываем краткое условие задачи.Выполняем рисунок.Записываем данные в круги (или

Слайд 16Спасибо за внимание!!!

Скачать презентацию

Теги

Разделы презентаций

Круги Эйлера и их практическое применение

Содержание

Слайды и текст этой презентации

Слайд 1Круги Эйлера
и их практическое применение

Слайд 2Выполнила:

Жубанова Диана
ученица 7 класса
Карасаевской СОШ

Слайд 3Цель исследования:
Изучить круги Эйлера
Научиться применять данный способ для решения задач

Cоставлять задачи практического содержания.
Задачи исследования:
Познакомиться с кругами Эйлера, кругами (диаграммами)

Слайд 4Немного об истории
Леонард Эйлер, крупнейший математик XVIII века, родился в

Швейцарии. В 1727г. по приглашению Петербургской академии наук он приехал

Слайд 5Немного об истории
Но наибольшего расцвета графические методы

достигли в сочинениях английского логика Джона Венна (1843 – 1923).

Слайд 6Применение простейших случаев кругов Эйлера - Венна

Слайд 7Применение простейших случаев кругов Эйлера - Венна

Слайд 8Применение простейших случаев кругов Эйлера - Венна

Слайд 9Задачи, решаемые с помощью кругов Эйлера - Венна
Задача

Слайд 10Задачи, решаемые с помощью кругов Эйлера - Венна
Задача №2.

Слайд 11Составление задач, имеющих практическое значение
Задача

Слайд 12Составление задач, имеющих практическое значение
Задача 3.
1)32-4=28(ч.) – играют хотя

бы в одну игру.
2)14-6-4-Х=4-Х (ч.) – играют только в баскетбол.
3)24-6-4-Х=14-Х

Слайд 13
Интеллектуальный марафон ,
заочный тур
60

Слайд 14Ты человек, а значит, ты
Обязан рассуждать –
А без логичной простоты
Ты

будешь пропадать.
Пусть за собой она зовёт –
Уйми в коленях дрожь!
Коль

Слайд 15Алгоритм решения задач с помощью кругов Эйлера - Венна
Заключение
Записываем краткое

условие задачи.
Выполняем рисунок.
Записываем данные в круги (или в диаграмму Эйлера).
Выбираем

Слайд 16Спасибо за внимание!!!

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Круги Эйлера и их практическое применение

Содержание

Слайды и текст этой презентации

Слайд 1Круги Эйлераи их практическое применение

Слайд 2Выполнила:Жубанова Диана ученица 7 классаКарасаевской СОШ

Слайд 3Цель исследования:Изучить круги ЭйлераНаучиться применять данный способ для решения задач

Cоставлять задачи практического содержания.Задачи исследования:Познакомиться с кругами Эйлера, кругами (диаграммами)

Слайд 4Немного об историиЛеонард Эйлер, крупнейший математик XVIII века, родился в

Швейцарии. В 1727г. по приглашению Петербургской академии наук он приехал

Слайд 5Немного об истории Но наибольшего расцвета графические методы

достигли в сочинениях английского логика Джона Венна (1843 – 1923).

Слайд 6Применение простейших случаев кругов Эйлера - Венна

Слайд 7Применение простейших случаев кругов Эйлера - Венна

Слайд 8Применение простейших случаев кругов Эйлера - Венна

Слайд 9Задачи, решаемые с помощью кругов Эйлера - ВеннаЗадача

Слайд 10Задачи, решаемые с помощью кругов Эйлера - ВеннаЗадача №2.

Слайд 11Составление задач, имеющих практическое значениеЗадача

Слайд 12Составление задач, имеющих практическое значениеЗадача 3. 1)32-4=28(ч.) – играют хотя

бы в одну игру.2)14-6-4-Х=4-Х (ч.) – играют только в баскетбол.3)24-6-4-Х=14-Х

Слайд 13Интеллектуальный марафон , заочный тур60

Слайд 14Ты человек, а значит, тыОбязан рассуждать –А без логичной простотыТы

будешь пропадать.Пусть за собой она зовёт –Уйми в коленях дрожь!Коль

Слайд 15Алгоритм решения задач с помощью кругов Эйлера - ВеннаЗаключениеЗаписываем краткое

условие задачи.Выполняем рисунок.Записываем данные в круги (или в диаграмму Эйлера).Выбираем

Слайд 16Спасибо за внимание!!!

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Круги Эйлера
и их практическое применение

Слайд 2Выполнила:

Жубанова Диана
ученица 7 класса
Карасаевской СОШ

Слайд 3Цель исследования:
Изучить круги Эйлера
Научиться применять данный способ для решения задач

Cоставлять задачи практического содержания.
Задачи исследования:
Познакомиться с кругами Эйлера, кругами (диаграммами)

Слайд 4Немного об истории
Леонард Эйлер, крупнейший математик XVIII века, родился в

Слайд 5Немного об истории
Но наибольшего расцвета графические методы

Слайд 9Задачи, решаемые с помощью кругов Эйлера - Венна
Задача

Слайд 10Задачи, решаемые с помощью кругов Эйлера - Венна
Задача №2.

Слайд 11Составление задач, имеющих практическое значение
Задача

Слайд 12Составление задач, имеющих практическое значение
Задача 3.
1)32-4=28(ч.) – играют хотя

бы в одну игру.
2)14-6-4-Х=4-Х (ч.) – играют только в баскетбол.
3)24-6-4-Х=14-Х

Слайд 13
Интеллектуальный марафон ,
заочный тур
60

Слайд 14Ты человек, а значит, ты
Обязан рассуждать –
А без логичной простоты
Ты

будешь пропадать.
Пусть за собой она зовёт –
Уйми в коленях дрожь!
Коль

Слайд 15Алгоритм решения задач с помощью кругов Эйлера - Венна
Заключение
Записываем краткое

условие задачи.
Выполняем рисунок.
Записываем данные в круги (или в диаграмму Эйлера).
Выбираем