Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Объем пирамиды
Содержание
- 1. Объем пирамиды
- 2. Найдем отношение объемовВо сколько раз увеличится объем
- 3. Основанием пирамиды является прямоугольник со сторонами 3
- 4. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .11
- 5. .Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен .22?
- 6. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза? Найдем отношение объемовh4h
- 7. .Объем правильной шестиугольной пирамиды 6. Сторона основания
- 8. .В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.61010
- 9. . Основанием пирамиды служит прямоугольник,
- 10. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое
- 11. Сторона основания правильной шестиугольной
- 12. Найдем отношение объемовОбъем параллелепипеда ABCDA1B1C1D1 равен 12. Найдите объем треугольной пирамиды B1ABC. BCDB1C1D1A1 12
- 13. Пирамида AD1CB1 получается, если мы отрежем от параллелепипеда четыре пирамиды
- 14. Объем куба равен 12. Найдите объем
- 15. От треугольной призмы, объем которой равен 150,
- 16. Объем треугольной пирамиды SABC, являющейся частью правильной
- 17. Объем правильной четырехугольной пирамиды SABCD равен 12.
- 18. Слайд 18
- 19. От треугольной пирамиды, объем
- 20. Найдем объем пирамиды NABC. Сравним его с
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Найдем отношение объемов
Во сколько раз увеличится объем правильного тетраэдра, если
все его ребра увеличить в два раза?
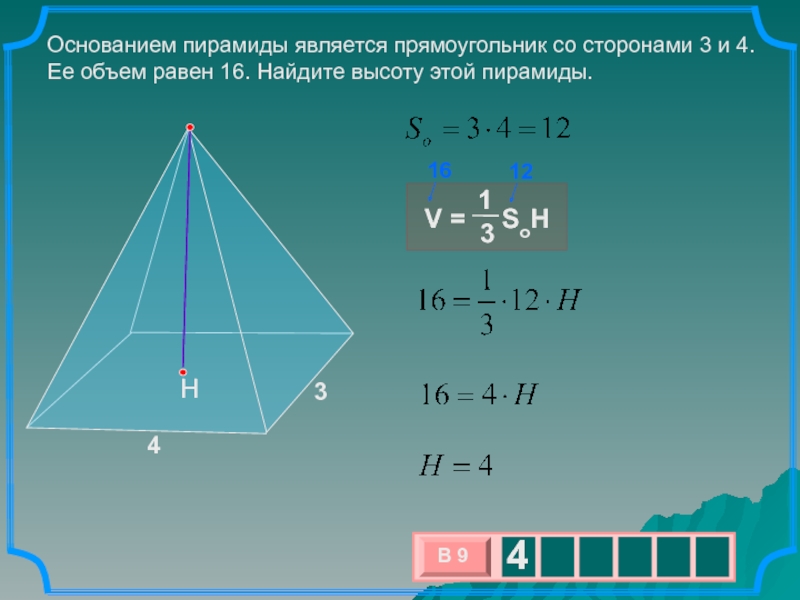
Слайд 3Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее
объем равен 16. Найдите высоту этой пирамиды.
3
4
Слайд 4Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1,
а высота равна .
1
1
Слайд 5
.
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2,
а объем равен .
2
2
?
Слайд 6
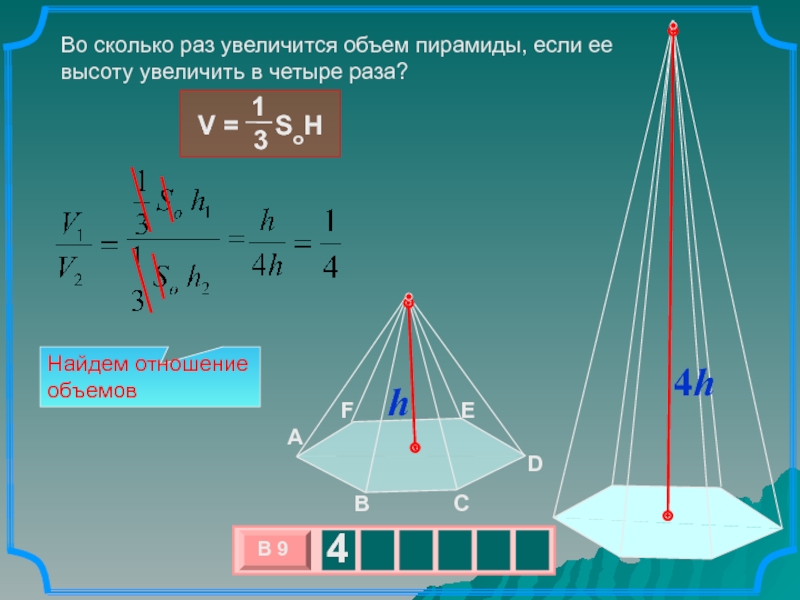
Во сколько раз увеличится объем пирамиды, если ее высоту увеличить
в четыре раза?
Найдем отношение
объемов
h
4h
Слайд 7
.
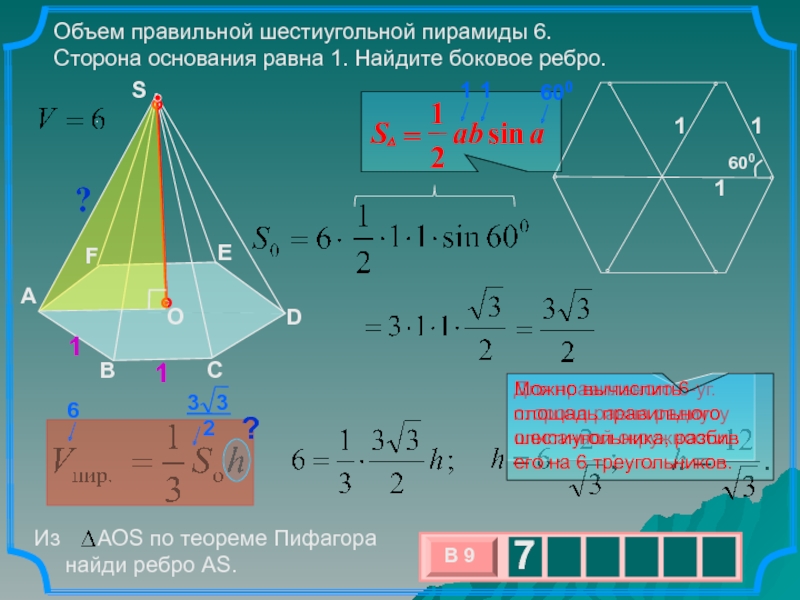
Объем правильной шестиугольной пирамиды 6.
Сторона основания равна 1. Найдите
боковое ребро.
A
F
B
C
D
E
1
1
?
1
S
О
Для правильного 6-уг. сторона равна радиусу описанной окружности.
Можно
вычислить площадь правильного шестиугольника, разбив его на 6 треугольников. Слайд 8
.
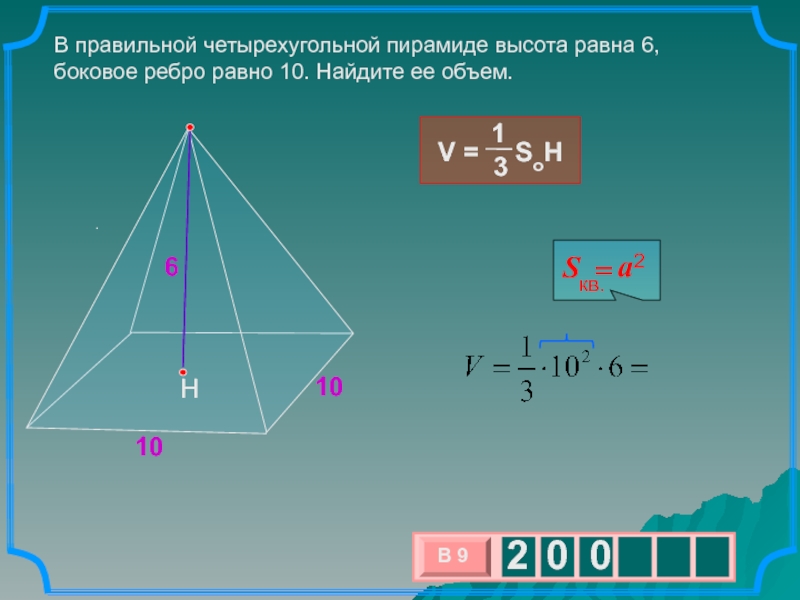
В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно
10. Найдите ее объем.
6
10
10
Слайд 9
.
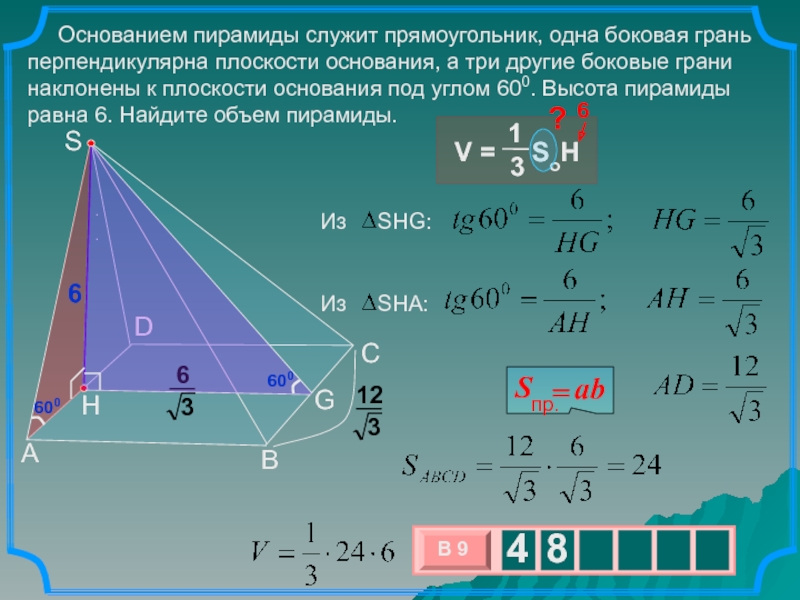
Основанием пирамиды служит прямоугольник, одна боковая грань
перпендикулярна плоскости основания, а три другие боковые грани наклонены к
плоскости основания под углом 600. Высота пирамиды равна 6. Найдите объем пирамиды..
S
D
C
B
G
6
A
Слайд 10
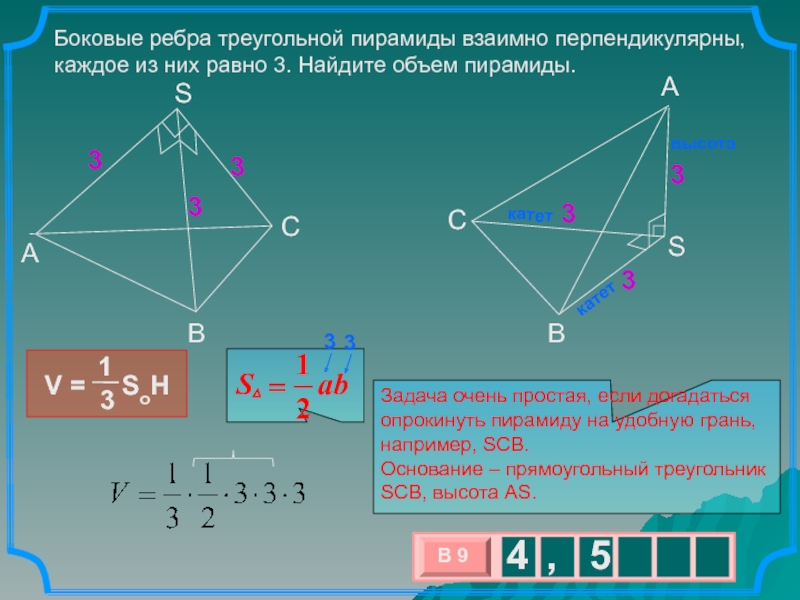
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно
3. Найдите объем пирамиды.
Задача очень простая, если догадаться опрокинуть
пирамиду на удобную грань, например, SCB. Основание – прямоугольный треугольник SCB, высота AS.
Слайд 11
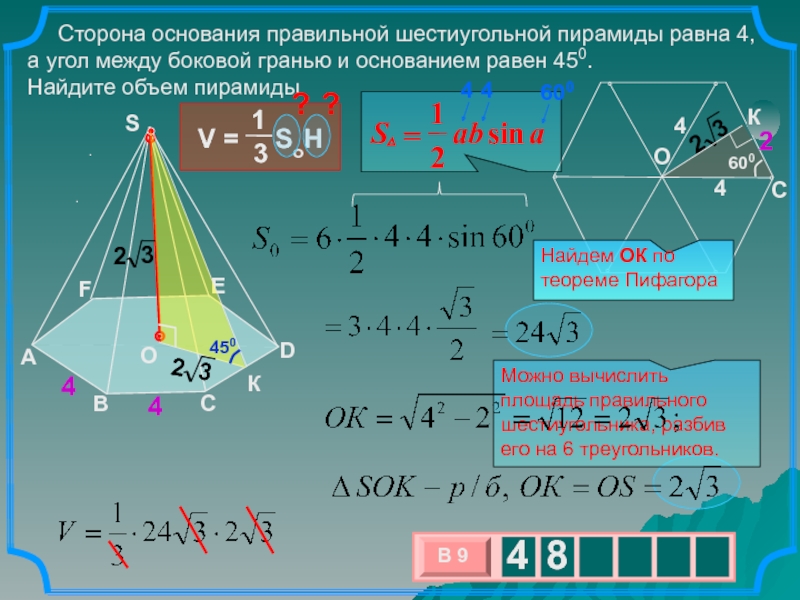
Сторона основания правильной шестиугольной пирамиды равна 4,
а угол между боковой гранью и основанием равен 450.
Найдите
объем пирамиды. .
.
A
F
B
C
D
E
4
4
S
О
К
Можно вычислить площадь правильного шестиугольника, разбив его на 6 треугольников.
Найдем ОК по теореме Пифагора
Слайд 12Найдем отношение объемов
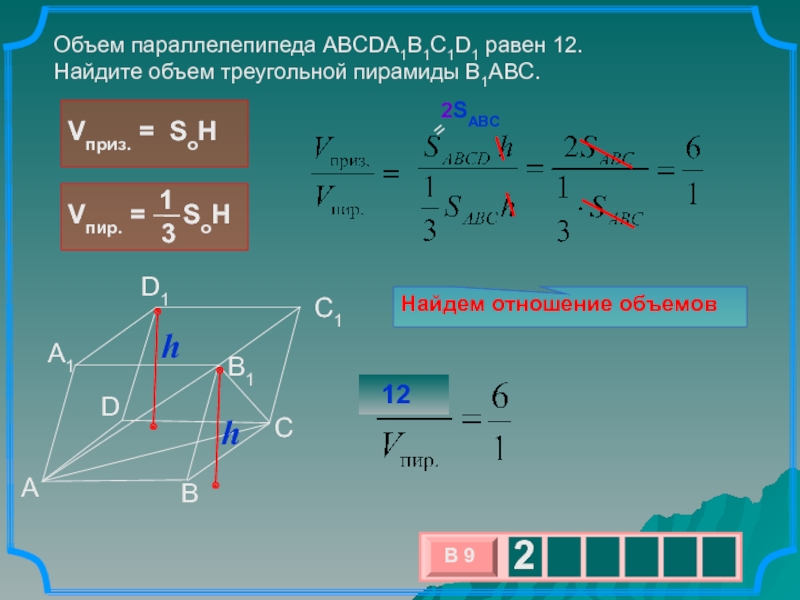
Объем параллелепипеда ABCDA1B1C1D1 равен 12.
Найдите объем треугольной
пирамиды B1ABC.
B
C
D
B1
C1
D1
A1
12
Слайд 13Пирамида AD1CB1 получается, если мы отрежем от параллелепипеда четыре пирамиды по углам — ABCB1, D1B1CC1,
AA1D1B1 и ADCD1. А объем каждой из них легко посчитать — мы делали это в предыдущей
задаче. Например, найдем объем пирамиды ABCB1.Объем параллелепипеда ABCDA1B1C1D1 равен 4,5. Найдите объем треугольной пирамиды AD1CB1.
C1
Найдем отношение объемов
4,5
Четыре пирамиды по углам — ABCB1, D1B1CC1, AA1D1B1 и ADCD1
Объем пирамиды АD1CB1
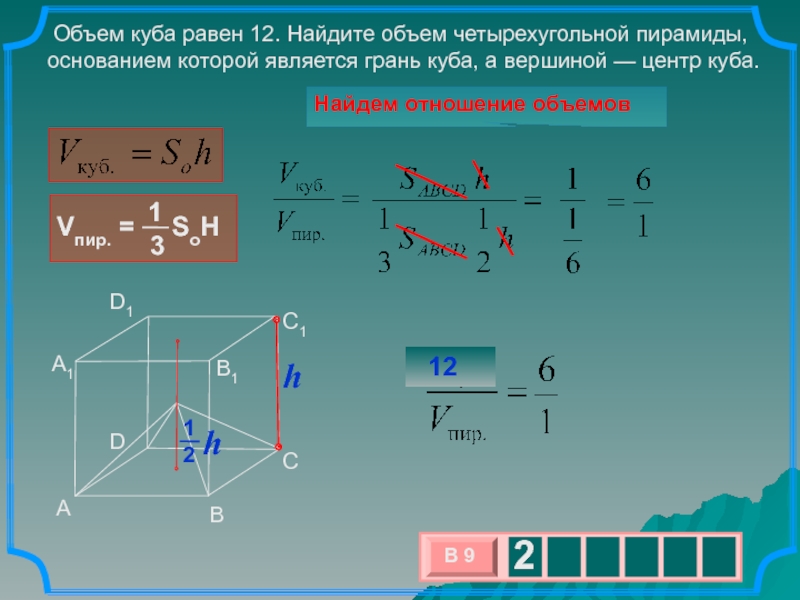
Слайд 14 Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием
которой является грань куба, а вершиной — центр куба.
Найдем отношение
объемовA
B
C
D
A1
B1
C1
D1
12
Слайд 15
От треугольной призмы, объем которой равен 150, отсечена треугольная пирамида
плоскостью, проходящей через сторону одного основания и противоположную вершину другого
основания.Найдите объем оставшейся части.
Найдем отношение объемов
150
Слайд 16Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF,
равен 8. Найдите объем шестиугольной пирамиды.
S
У треугольной и шестиугольной пирамид, о которых говорится
в условии, одинаковые высоты. Убедимся в этом, изменим расположение букв…Одинаковая высота, но площадь оснований различна.
Найдем отношение объемов
8
V1
V2
Поработаем с выносным чертежом. Видим, что площадь основания треугольной пирамиды в 6 раз меньше, чем у шестиугольной.
Слайд 17
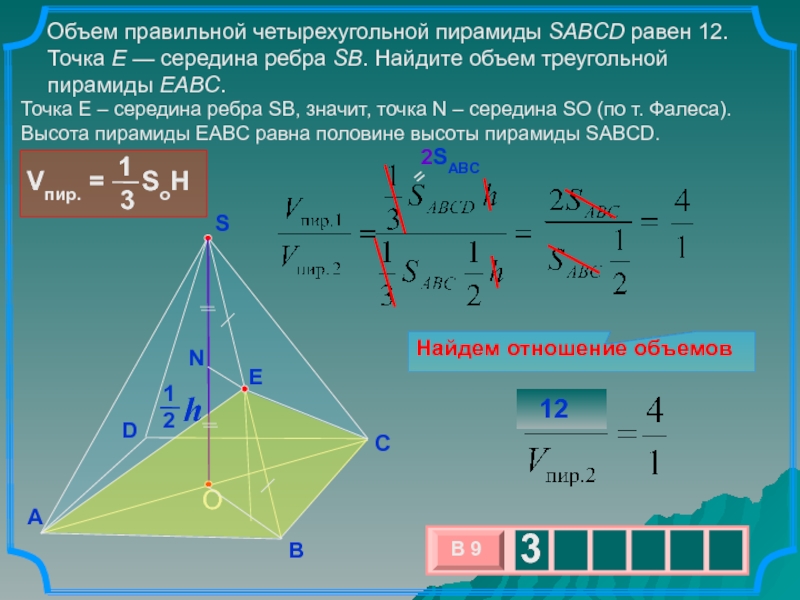
Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина
ребра SB. Найдите объем треугольной пирамиды EABC.
S
B
D
A
C
Точка E –
середина ребра SB, значит, точка N – середина SO (по т. Фалеса). Высота пирамиды EABC равна половине высоты пирамиды SABCD.
E
N
Найдем отношение объемов
12
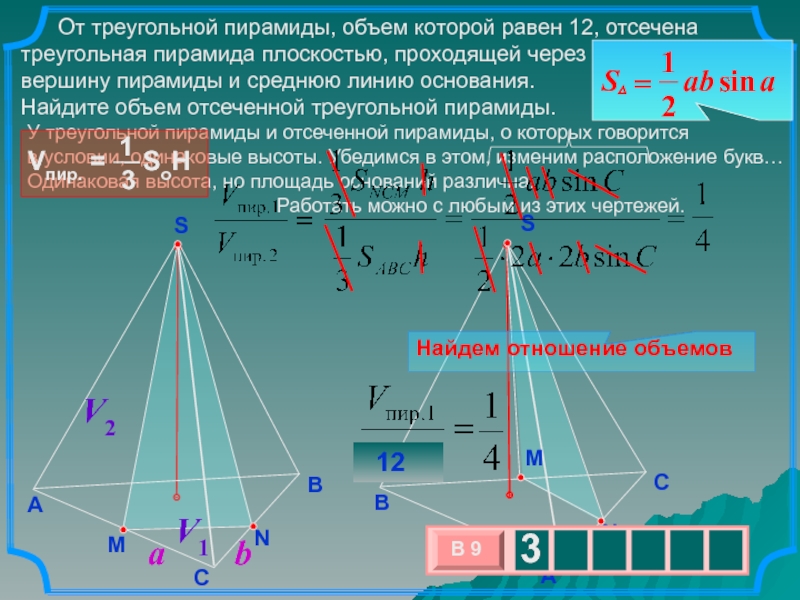
Слайд 19 От треугольной пирамиды, объем которой равен 12,
отсечена треугольная пирамида плоскостью, проходящей через
вершину пирамиды и среднюю
линию основания. Найдите объем отсеченной треугольной пирамиды.
B
У треугольной пирамиды и отсеченной пирамиды, о которых говорится в условии, одинаковые высоты. Убедимся в этом, изменим расположение букв… Одинаковая высота, но площадь оснований различна.
Работать можно с любым из этих чертежей.
Найдем отношение объемов
12
V2
V1
Слайд 20
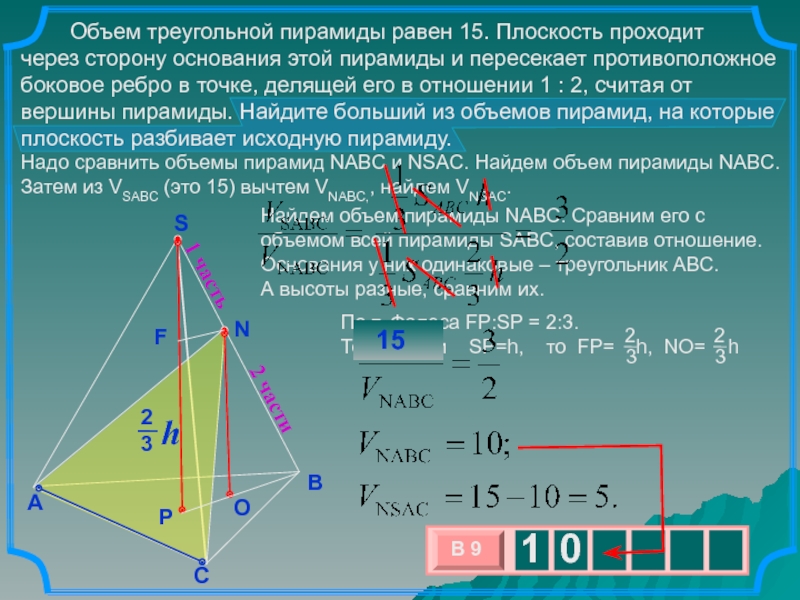
Найдем объем пирамиды NABC. Сравним его с объемом всей пирамиды
SABC, составив отношение.
Основания у них одинаковые – треугольник АВС.
А высоты
разные, сравним их. Объем треугольной пирамиды равен 15. Плоскость проходит
через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.
S
C
A
B
Надо сравнить объемы пирамид NABC и NSAC. Найдем объем пирамиды NABC. Затем из VSABC (это 15) вычтем VNABC,, найдем VNSAC.
15