Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Показательная функция и её применение
Содержание
- 1. Показательная функция и её применение
- 2. 2. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ И ЕЁ ПРИМЕНЕНИЕ В ПРИРОДЕ И ТЕХНИКЕ.1. Показательная функция.3. В биологии.4. В экономике.
- 3. Некоторые наиболее часто встречающиеся виды трансцендентных функций,прежде всего показательные,открывают доступ ко многим исследованиям.Л.Эйлер.«Показательная функция».
- 4. Графики функции у=2х и у=(½)х График функции
- 5. Блиц – опрос1.Какая функция называется показательной?2.Какова область
- 6. Какие из перечисленных функций являются возрастающими, а какие убывающими?
- 7. Какие из функций являются возрастающими, а какие убывающими?
- 8. Показательные уравнения. Уравнения,у которых неизвестное
- 9. Решите уравнения ( устно):5 х =25х=27 х-2
- 10. Указать способы решения показательных уравнений.
- 11. Диагностика уровня формирования практических навыков
- 12. Чтобы решить графически уравнение
- 13. Слайд 13
- 14. Определение Показательные неравенства – это неравенства, в которых неизвестное содержится в показателе степени.Примеры:
- 15. Показательные неравенства решаются по следующим свойствам
- 16. Решите неравенства (устно):2 х > 0 x-
- 17. Решения показательных неравенств:Способ Уравнивание оснований правой и
- 18. Решите неравенство:
- 19. Решите неравенство:
- 20. Решение показательных неравенствСпособ 2: Вынесение за скобки
- 21. Решение показательных неравенствСпособ 3: введение новой переменнойОтвет: х < 2. х>03>1, то
- 22. И её применение в природе и технике.Показательная функция
- 23. Подумайте! Где может использоваться показательная функция?Тема «Показательная
- 24. Наглядный бытовой пример!Все, наверное, замечали, что если
- 25. При падении тел в безвоздушном пространстве скорость
- 26. Рассмотрим задачу о падении парашютиста. Если считать,
- 27. Много трудных математических задач приходится решать в
- 28. Если не учитывать сопротивление воздуха и притяжение
- 29. Если при колебаниях маятника, гири, качающейся на
- 30. Когда радиоактивное вещество распадется, его количество уменьшается.
- 31. Задача:Период полураспада плутония равен 140 суткам. Сколько
- 32. Как видите, во всех
- 33. Вот некоторые из Нобелевских лауреатов, получивших премию
- 34. Она не перестаёт нас удивлять!Показательная функция также
- 35. Применение показательной функции в биологии .
- 36. Применение логарифмической функции в биологии.В питательной
- 37. Применение показательной функции в экономике
- 38. Задача:Ежемесячно на банковский вклад, равный S0 рублей
- 39. А теперь,
- 40. ДОМАШНЕЕ ЗАДАНИЕСтраница 57 учебника – «ПРОВЕРЬ СЕБЯ»
- 41. СПАСИБО ЗА УРОК!
- 42. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Выполнила
Учитель математики I категории
МБОУ Федосеевской СОШ
Лозовая Раиса Михайловна
Показательная функция
и
её применение
Слайд 22. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
И ЕЁ ПРИМЕНЕНИЕ В ПРИРОДЕ И
ТЕХНИКЕ.
1. Показательная функция.
3. В биологии.
4. В экономике.
Слайд 3Некоторые наиболее часто
встречающиеся виды
трансцендентных функций,
прежде всего показательные,
открывают доступ
ко
многим исследованиям.
Л.Эйлер.
«Показательная функция».
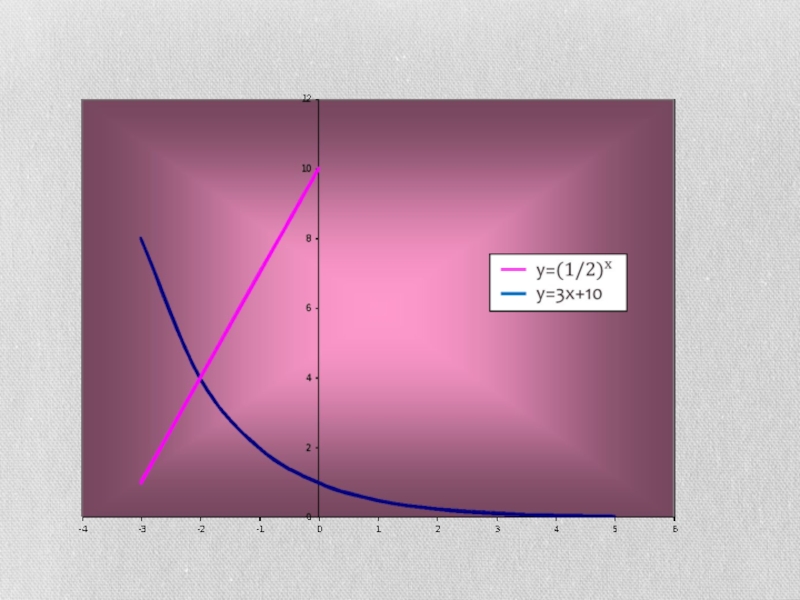
Слайд 4Графики функции у=2х и у=(½)х
График функции у=2х проходит через
точку (0;1) и расположен выше оси Ох.
а>1
Д(у): х є RЕ(у): у >0
Возрастает на всей области определения.
График функции у= также проходит через точку (0;1) и расположен выше оси Ох.
0<а<1 Д(у): х є R
Е(у): у>0
Убывает на всей области определения.
Слайд 5Блиц – опрос
1.Какая функция называется показательной?
2.Какова область определения функции y=0,3x?
3.Каково
множество значения функции y=3x?
4. Дайте определение возрастающей, убывающей функции.
5.При каком
условии показательная функция является возрастающей?6.При каком условии показательная функция является убывающей?
7.Возрастает или убывает показательная функция
8.Определить при каком значении a функция
проходит через точку А(1; 2);
9
Слайд 8 Показательные уравнения. Уравнения,у которых неизвестное находится в показателе степени,
называются показательными.
Способы решения:
По свойству степени;
Вынесение общего множителя за скобки;
Деление обеих
частей уравнения на одно и то же выражение, принимающее значение отличное от нуля при всех действительных значениях х;Способ группировки;
Сведение уравнения к квадратному;
Графический.
.
Например:
Слайд 9Решите уравнения ( устно):
5 х =25
х=2
7 х-2 =49
х=4
4 х =1
х
= 0
5,7 х-3 = 1
х = 3
2 2 х
=64х = 5
3 9 х =81
х = 1,5
5 х =7 х
х = 0
3,4 х+2 =4,3 х+2
х = -2
Слайд 12 Чтобы решить графически уравнение f (x) = g (x) ,
надо:
построить графики функций у = f (x) и у
= g (x)найти абсциссу точки пересечения графиков функций
рассмотреть возможность существования других точек пересечения
Слайд 14Определение
Показательные неравенства –
это неравенства, в которых
неизвестное содержится в показателе степени.
Примеры:
Слайд 15Показательные неравенства
решаются по следующим свойствам показательной функции:
•если а > 1 , то неравенство
a х 1 < а х 2справедливо х 1< х 2
•если 0 < а < 1, то неравенство a х 1 > а х 2
справедливо х 1< х 2
Слайд 16Решите неравенства (устно):
2 х > 0
x- любое
2x >1
x
> 0
х 1
х
0х < 0
x= Ø
5 x >25
x > 2
0,7 x < 0,49
x > 2
0,2 x+1 < 0,2 4
x > 3
9,7 x-2 < 9,7 10
x < 12
Слайд 20Решение показательных неравенств
Способ 2: Вынесение за скобки степени с меньшим
показателем
Ответ: х >3
3 > 1, то
: 10
Слайд 23Подумайте! Где может использоваться показательная функция?
Тема «Показательная функция» является основополагающей
при изучении таких тем, как «Производная показательной функции», «Термодинамика», «Электромагнетизм»,
«Ядерная физика», «Колебания», используется для решения некоторых задач судовождения.Слайд 24Наглядный бытовой пример!
Все, наверное, замечали, что если снять кипящий чайник
с огня, то сначала он быстро остывает, а потом остывание
идет гораздо медленнее. Дело в том, что скорость остывания пропорциональна разности между температурой чайника и температурой окружающей среды. Чем меньше становится эта разность, тем медленнее остывает чайник. Если сначала температура чайника равнялась То, а температура воздуха T1, то через t секунд температура Т чайника выразится формулой:T=(T1-T0)e-kt+T1,
где k - число, зависящее от формы чайника, материала, из которого он сделан, и количества воды, которое в нем находится.
Слайд 25При падении тел в безвоздушном пространстве скорость их непрерывно возрастает.
При
падении тел в воздухе скорость падения тоже увеличивается, но не
может превзойти определенной величины.Слайд 26
Рассмотрим задачу о падении парашютиста. Если считать, что сила сопротивления
воздуха пропорциональна скорости падения парашютиста, т.е. что F=kv , то
через t секунд скорость падения будет равна: v=mg/k(1-e-kt/m), где m - масса парашютиста. Через некоторый промежуток времени е-kt/m станет очень маленьким числом, и падение станет почти равномерным. Коэффициент пропорциональности k зависит от размеров парашюта. Данная формула пригодна не только для изучения падения парашютиста, но и для изучения падения капли дождевой воды, пушинки и т.д.Слайд 27Много трудных математических задач приходится решать в теории межпланетных путешествий.
Одной из них является задача об определении массы топлива, необходимого
для того, чтобы придать ракете нужную скорость v. Эта масса М зависит от массы m самой ракеты (без топлива) и от скорости v0, с которой продукты горения вытекают из ракетного двигателя.Слайд 28Если не учитывать сопротивление воздуха и притяжение Земли, то масса
топлива определиться формулой: M=m(ev/v0-1) (формула К.Э.Циалковского). Например, для того чтобы
ракете с массой 1,5 т придать скорость 8000 м/с, надо при скорости истечения газов 2000 м/с взять примерно 80 т топлива.Слайд 29Если при колебаниях маятника, гири, качающейся на пружине, не пренебрегать
сопротивлением воздуха, то амплитуда колебаний становится все меньше, колебания затухают.
Отклонения точки, совершающей затухающие колебания, выражается формулой: s=Ae-ktsin(?t+?). Так как множитель е-kt уменьшается с течением времени, то размах колебаний становится все меньше и меньше.Слайд 30Когда радиоактивное вещество распадется, его количество уменьшается. Через некоторое время
остается половина первоначального количества вещества. Этот промежуток времени to называется
периодом полураспада. Вообще через t лет масса m вещества будет равна: m=m0(1/2)t/t0, где m0 - первоначальная масса вещества. Чем больше период полураспада, тем медленнее распадается вещество.Явление радиоактивного распада используется для определения возраста археологических находок, например, определен примерный возраст Земли, около 5,5 млрд. лет, для поддержания эталона времени.
Слайд 31Задача:
Период полураспада плутония равен 140 суткам. Сколько плутония останется через
10 лет, если его начальная масса равна 8г ?
Слайд 33Вот некоторые из Нобелевских лауреатов, получивших премию за исследования в
области физики с использованием показательной функции:
Пьер Кюри - 1903 г.
Ричардсон Оуэн - 1928 г.
Игорь Тамм - 1958 г.
Альварес Луис - 1968 г.
Альфвен Ханнес - 1970 г.
Вильсон Роберт Вудро - 1978 г.
Слайд 34Она не перестаёт нас удивлять!
Показательная функция также используется при решении
некоторых задач судовождения, например, функцию е-x используют в задачах, требующих
применения биноминального закона (повторение опытов), закона Пуассона (редких событий), закона Релея (длина случайного вектора).Слайд 36Применение логарифмической
функции в биологии.
В питательной среде бактерия кишечной палочки
делится каждую минуту. Понятно, что общее число бактерий за каждую
минуту удваивается. Если в начале процесса была одна бактерия, то через х минут их число (N) станет равной 2х , т.е. N(х) = 2х.Слайд 38Задача:
Ежемесячно на банковский вклад, равный S0 рублей начисляется р%. На
сколько процентов возрастет банковский вклад за х месяцев?
Решение.
Слайд 39
А теперь, в конце урока хочется, чтобы вы
выразили свое отношение к нашей сегодняшней работе и всему уроку
в целом. Ответьте на вопросы в листах рефлексии и сдайте их мне.2) Поставь оценку учителю за работу по 10 бальной системе.
3) Поставь оценку себе за работу по 10 бальной системе.
Понравилось на уроке? (отметь галочкой мордашку)