Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сферическая тригонометрия
Содержание
- 1. Сферическая тригонометрия
- 2. Слайд 2
- 3. СодержаниеI. Введение
- 4. Слайд 4
- 5. Цели:1.Показать историю зарождения, и продвижение «сферической тригонометрии»
- 6. СФЕРИКА И СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ В ДРЕВНОСТИ ИНА СРЕДНЕВЕКОВОМ
- 7. Из всех древних сочинений о сферике наибольшую
- 8. Слайд 8
- 9. ГЕОМЕТРИЯ ЛОБАЧЕВСКОГОЛобачевский Николай Иванович (1792-1856), русский математик,
- 10. НАЧАЛЬНЫЕ ПОНЯТИЯ СФЕРИЧЕСКОЙГЕОМЕТРИИ.Сферой
- 11. Слайд 11
- 12. Слайд 12
- 13. Т е о р е м а
- 14. СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯДлины сторон и величины углов произвольного
- 15. Слайд 15
- 16. Теорема Эйлера. Если В — число вершин
- 17. ПРИМЕНЕНИЯ СФЕРИЧЕСКОЙ ГЕОМЕТРИИ В НАВИГАЦИИ И КАРТОГРАФИИ
- 18. Навигация (это слово происходит от латинского navigatio
- 19. Хотя- ортодромия и является кратчайшим путем на
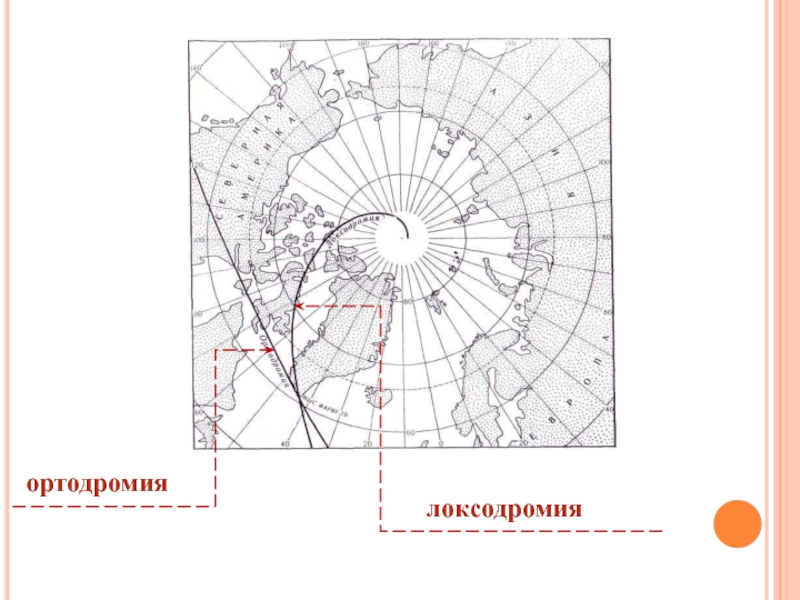
- 20. ортодромиялоксодромия
- 21. При решении многих практических задач Землю удобно
- 22. Слайд 22
- 23. Карту, выполненную в меркаторской проекции, можно получить
- 24. Слайд 24
- 25. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ Исаев А. Геометрия Лобачевского
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2
МОУ СОШ №5
Выполнил ученик 11 «В» класса
Грак Д.В.
Проверил учитель математики
Якушева Е.Б
Торжок
2008г.
Слайд 3 Содержание
I. Введение
II.Основная часть
1. Сферика и сферическая тригонометрия в древности
2. Геометрия Лобачевского
2.1. Лобачевский Н.И.
2.2. 5 постулат сферической тригонометрии
3. Начальные понятия сферической геометрии
4.Соответствие между сферической геометрией и планиметрией
5. Сферическая тригонометрия
6. Площади сферических многоугольников и формула Эйлера
7. Применения сферической геометрии в навигации
8. Картографические проекции
III. Заключение
IV. Список использованной литературы
Слайд 4
ВВЕДЕНИЕ
«Напрасное
старание со времен Евклида в продолжении двух тысяч лет заставило меня подозревать,
что в самих понятиях еще не заключается той истины,
которую хотели доказать и которую проверить,
подобно другим физическим законам, могут лишь опыты,
каковы, например, Астрономические наблюдения.
В справедливости моей догадки будучи наконец убежден и
почитая затруднительный вопрос решенным вполне,
писал об этом я рассуждение в 1826 году».
(Лобачевский Н.И.)
Слайд 5
Цели:
1.Показать историю зарождения, и продвижение
«сферической тригонометрии» как науки,
на
протяжении большого отрезка времени.
2.Описать биографию Лобачевского и привести его заслуги
в науке.
3.Сравнение «сферической геометрии» с планиметрией.
4.Показать значимость этой науки в практической сфере.
Слайд 6
СФЕРИКА И СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ В ДРЕВНОСТИ И
НА СРЕДНЕВЕКОВОМ ВОСТОКЕ.
ЕВКЛИД (умер между
275 и 270 до н. э.), древнегреческий математик. Работал в
Александрии в 3 в. до н. э. Главный труд «Начала» (15 книг), содержащий основы античной математики, элементарной геометрии, теории чисел, общей теории отношений и метода определения площадей и объемов, включавшего элементы теории пределов, оказал огромное влияние на развитие математики. Работы по астрономии, оптике, теории музыки.Слайд 7Из всех древних сочинений о сферике наибольшую роль в истории
науки сыграла «Сферика» Менелая, работавшего в Александрии в I в.
н. э. и обобщившего все результаты, которые были получены в этой области до него. В его сочинении не только изложена геометрия на сфере, но впервые введен сферический треугольник, последовательно доказаны теоремы, служившие базой сферической тригонометрии, и создана теоретическая основа для тригонометрических вычислений [5, 15].Сведения о жизни Менелая крайне скудны. Известно, что в 98 г. он производил
астрономические наблюдения в Риме. «Сферика», его основное произведение, в греческом
оригинале не сохранилась и известна лишь по средневековым арабским переводам.
Теорема Менелая для плоского случая формулируется следующим образом: пусть даны
взаимно пересекающиеся прямые AB, AC, BE и CD, образующие фигуру ACGB (рис.);
тогда имеют место соотношения:
СЕ / АЕ = СG / DG * DB / AB, CA / AE = CD / DG * GB / BE
Для сферического случая в теореме фигурируют, как было принято в греческой тригонометрии,
хорды удвоенных дуг. Если дана фигура ACGB (рис.), образованная дугами больших кругов на
поверхности сферы, то справедливы соотношения:
хорда(2СЕ) / хорда(2АЕ) = хорда(2CG) / хорда(2DG) * хорда(2DB) / хорда(2АВ)
хорда(2АС) / хорда(2АЕ) = хорда(2CD) / хорда(2DG) * хорда(2GB) / хорда(2ВЕ)
Слайд 9ГЕОМЕТРИЯ ЛОБАЧЕВСКОГО
Лобачевский Николай Иванович (1792-1856), русский математик, создатель неевклидовой геометрии
(геометрии Лобачевского). Ректор Казанского университета (1827-46). Открытие Лобачевского (1826, опубликованное
1829-30), не получившее признания современников, совершило переворот в представлении о природе пространства, в основе которого более 2 тыс. лет лежало учение Евклида, и оказало огромное влияние на развитие математического мышления. Труды по алгебре, математическому анализу, теории вероятностей, механике, физике и астрономии.Слайд 10
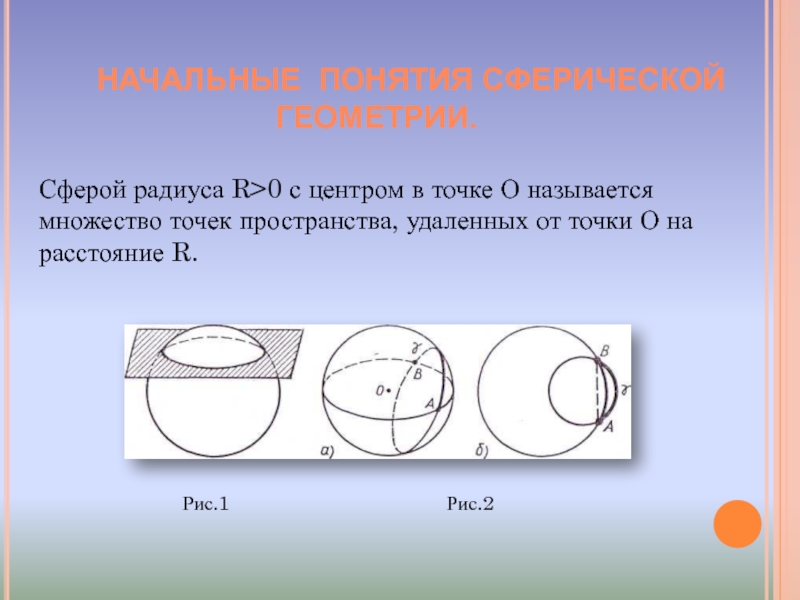
НАЧАЛЬНЫЕ ПОНЯТИЯ СФЕРИЧЕСКОЙ
ГЕОМЕТРИИ.
Сферой радиуса R>0 с
центром в точке О называется множество точек пространства, удаленных от
точки О на расстояние R.Рис.1 Рис.2
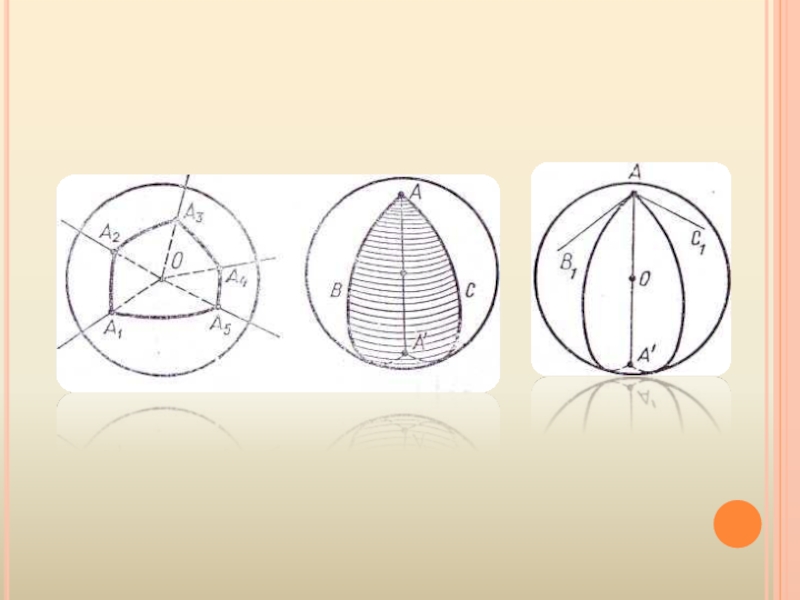
Слайд 12 СООТВЕТСТВИЕ МЕЖДУ СФЕРИЧЕСКОЙ
ГЕОМЕТРИЕЙ И ПЛАНИМЕТРИЕЙ
В планиметрии понятие прямой
не определяется — это первичное понятие геометрии плоскости. Требуется, однако, чтобы для прямых на плоскости выполнялись некоторые аксиомы. Выясним, какие из этих аксиом будут справедливы в сферической геометрии—для сферических прямых.Конечно, аксиома, гласящая, что каждая прямая есть множество точек, в сферической геометрии выполняется — большие окружности суть множества точек. Однако уже со следующей аксиомой: для любых двух точек А и В существует единственная содержащая эти точки прямая — дело обстоит сложнее. Если точки А и В сферы не являются диаметрально противоположными, то это предложение верно (объясните почему), но для диаметрально противоположных точек А и В существует бесконечно много сферических прямых, содержащих эти точки: пересечение сферы с
любой плоскостью, содержащей диаметр АВ, даст такую прямую. Можно сказать, что эта аксиома «почти» выполняется на сфере. Оговорка «почти» приводит к замечательным следствиям.
Слайд 13Т е о р е м а . Любые две
различные прямые на сфере (т. е. противоположных точках сферы.
Доказательство. Если
α и β — плоскости двух различных больших окружностей на сфере (О, R), то 0ϵα и Oϵβ, поэтому α и β пересекаются по некоторой прямой l, проходящей через центр сферы. Прямая l пересекается со сферой в двух диаметрально противоположных точках, которые и будут общими точками рассматриваемых больших окружностей.Слайд 14СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ
Длины сторон и величины углов произвольного треугольника па плоскости
связаны между собой определенными соотношениями, важнейшие из которых называются теоремами
косинусов и синусов:c2=a2+b2-2ab cos^C,
a/sin^A = b/sin^B = c/sin^C.
Теорема косинусов сферической тригонометрии
cosγ = cosαcosβ+sinαsinβcos^C.
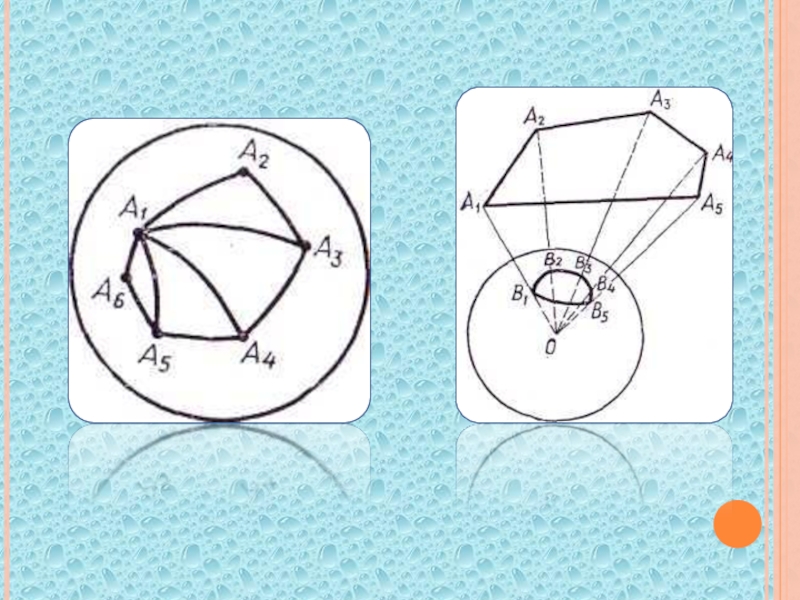
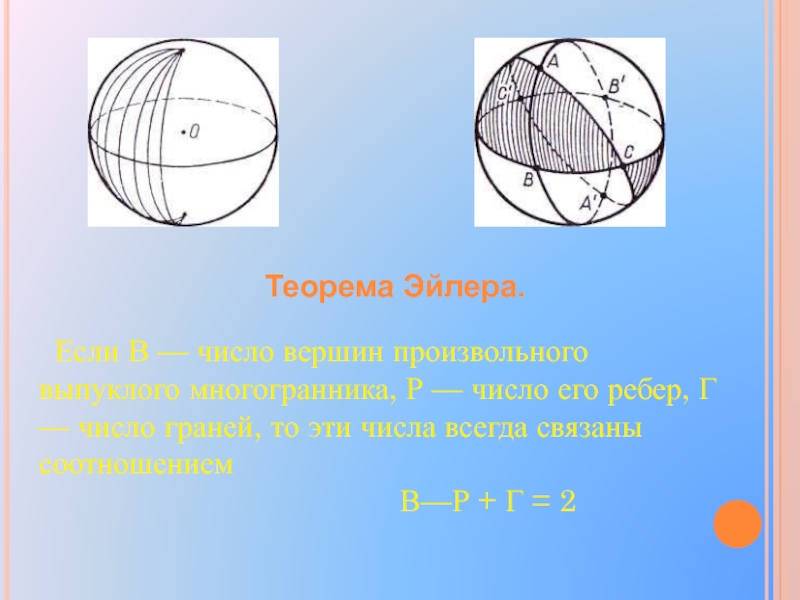
Слайд 16Теорема Эйлера.
Если В — число вершин произвольного выпуклого многогранника,
Р — число его ребер, Г — число граней, то
эти числа всегда связаны соотношениемВ—Р + Г = 2
Слайд 18Навигация (это слово происходит от латинского navigatio — плыву на
судне) — одна из наиболее древних наук. Простейшие задачи навигации,
такие, например, как определение кратчайшего маршрута, выбор направления движения, встали перед самыми первыми мореплавателями. В настоящее время эти же и другие задачи приходится решать не только морякам, но и летчикам, и космонавтам.Слайд 19Хотя- ортодромия и является кратчайшим путем на сфере, самолеты и
корабли движутся иными маршрутами. Дело в том, что ортодромия, отличная
от дуги меридиан;! или экватора, пересекает различные меридианы под различными углами, и, следовательно, при движении по ортодромии приходится непрерывно менять курс. Это, конечно, практически неосуществимо. Намного проще плавать по постоянному курсу. Кривые, которые пересекают все меридианы под постоянным углом, называют локсодромиями (в переводе «косой бег»). На рисунке 15 показана локсодромия, пересекающая все меридианы под углом 70°. Конечно, при движении по локсодромиям путь удлиняется. Но если пункты А и В находятся сравнительно близко друг от друга, то удлинение пути по сравнению с движением по ортодромии А В довольно незначительно.Слайд 21При решении многих практических задач Землю удобно считать шаром. Уменьшая
этот шар примерно в 10 млн. раз и изображая очертания
материков и океанов, озер и рек и т. д., получим глобус. Но пользоваться глобусом далеко не всегда удобно. Основная задача картографии состоит в возможно более точном изображении поверхности глобуса на плоскости. При этом возникает целый ряд трудностей, которые вынуждают искать самые разные способы изображения карт.Основную причину этих трудностей можно увидеть на наглядном примере. Как бы мы ни пытались наложить сколь угодно малый кусочек резинового мяча или шарика для игры в пинг-понг на поверхность стола, это никак не удается сделать без разрывов, растяжений или налегания отдельных частей друг на друга. На языке математики это означает:
Если подмножество ω сферы содержит сферический сегмент, то ω нельзя отобразить на плоскую фигуру с сохранением расстояний.
Слайд 23Карту, выполненную в меркаторской проекции, можно получить и без предварительного
стереографического проектирования. Покажем, например, как изготовить такую карту приэкваториальных областей
Земли.
Этот способ основан на том, что цилиндрические поверхности можно развернуть на плоскость. Рассмотрим цилиндр с осью l, касающийся глобуса. Срезав полярные области, можно оставшуюся часть сферы спроектировать из ее центра на поверхность цилиндра. Разрежем цилиндрическую поверхность по образующей и развернем ее на плоскость (рис.22). Очевидно, что в результате сетка параллелей и меридианов отображается на прямоугольную сетку. Правда, углы при этом не сохраняются, но можно получить и конформное отображение участка сферы на плоскость — меркаторскую проекцию. Этот вид картографических проекций называют также цилиндрической равноугольной проекцией.
Слайд 25СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
Исаев А. Геометрия Лобачевского
Матвиевская Г.П.
Сферика и сферическая тригонометрия в древности и
на средневековом
востоке; 1979 г.Рудников В.А Большая энциклопедия Кирилла и Мефодия; 2006г.
Шварцбург С.И. Избранные вопросы математики; 1980 г.