Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Скалярное произведение векторов
Содержание
- 1. Скалярное произведение векторов
- 2. αОУгол между векторами
- 3. 300 3001200 900 1800 00 Найдите угол между векторами
- 4. Скалярное произведение векторов – число (скаляр).Скалярным произведением
- 5. = 0 Скалярное произведение ненулевых векторов равно
- 6. Скалярное произведение ненулевых векторов положительно тогда и
- 7. Скалярное произведение ненулевых векторов отрицательно тогда и
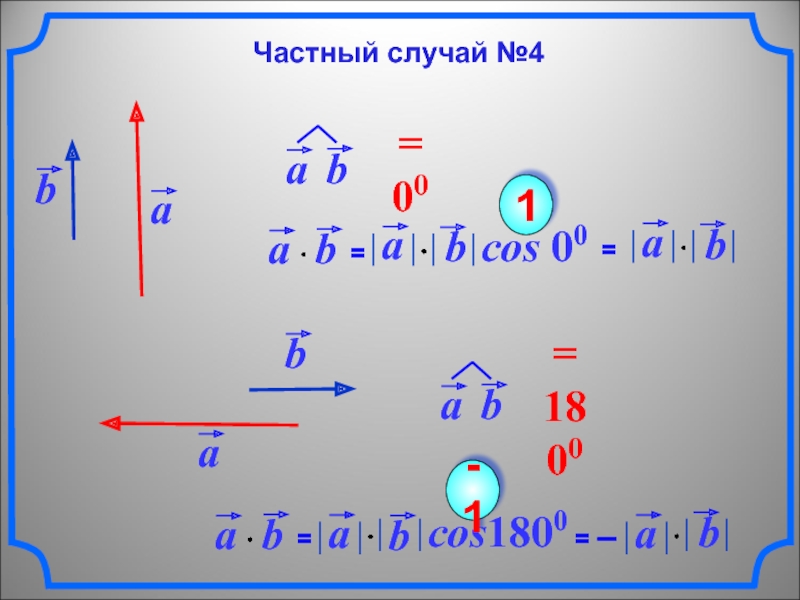
- 8. cos 001cos1800-1Частный случай №4
- 9. cos00 1Таким образом, скалярный квадрат вектора равен
- 10. Все ребра тетраэдра АВСD равны друг
- 11. Формула для нахождения скалярного произведениячерез координаты векторов=
- 12. Пример №1Найти скалярное произведение векторов:a {-6; 9;
- 13. Пример №2Найти скалярное произведение векторов:a {0; 0;
- 14. Пример №3Найти скалярное произведение векторов:a {1; 7;
- 15. Проверочная работа1. Найти скалярное произведение векторов:a {1; 10; 7}b {0; 7; 0}
- 16. Проверочная работа2. Найти скалярное произведение векторов:a {7; 25; 0}b {11; 0; 54}
- 17. Проверочная работа3. Найти скалярное произведение векторов:a {|-2|; 0; |3|}b {1; |-11|; 1}
- 18. Проверочная работа4. Найти скалярное произведение векторов:a {sin(900); 2; 3}b {3; 2; 1}
- 19. Проверочная работа5. Найти скалярное произведение векторов:a {-1; 2; 8}b {5; 5; 0}
- 20. Проверочная работаРабота закончена.Перейдём к проверке.
- 21. Проверочная работа1. Найти скалярное произведение векторов:a {1; 10; 7}b {0; 7; 0} 10 7 = 70
- 22. Проверочная работа2. Найти скалярное произведение векторов:a {7; 25; 0}b {11; 0; 54} 7 11 = 77
- 23. Проверочная работа3. Найти скалярное произведение векторов:a {|-2|;
- 24. Проверочная работа4. Найти скалярное произведение векторов:a {sin(900);
- 25. Проверочная работа5. Найти скалярное произведение векторов:a {-1;
- 26. Домашнее заданиеЧитать п.51Выполнить упр.446(б), упр.448
- 27. Скачать презентанцию
αОУгол между векторами
Слайды и текст этой презентации
Слайд 4Скалярное произведение векторов – число (скаляр).
Скалярным произведением двух векторов называется
произведение
Слайд 5
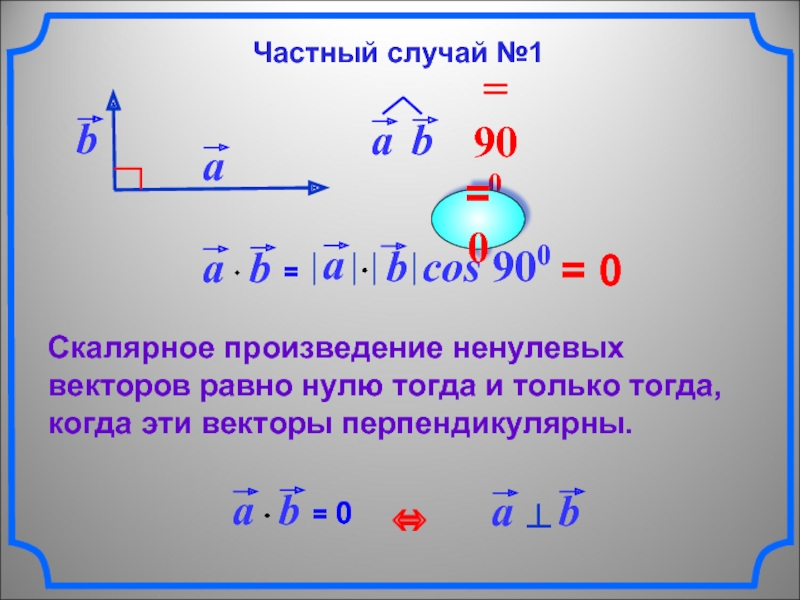
= 0
Скалярное произведение ненулевых векторов равно нулю тогда и
только тогда, когда эти векторы перпендикулярны.
Частный случай №1
= 0
Слайд 6
Скалярное произведение ненулевых векторов положительно тогда и только тогда, когда
угол между векторами острый.
cos
α
> 0
> 0
Частный случай №2
Слайд 7
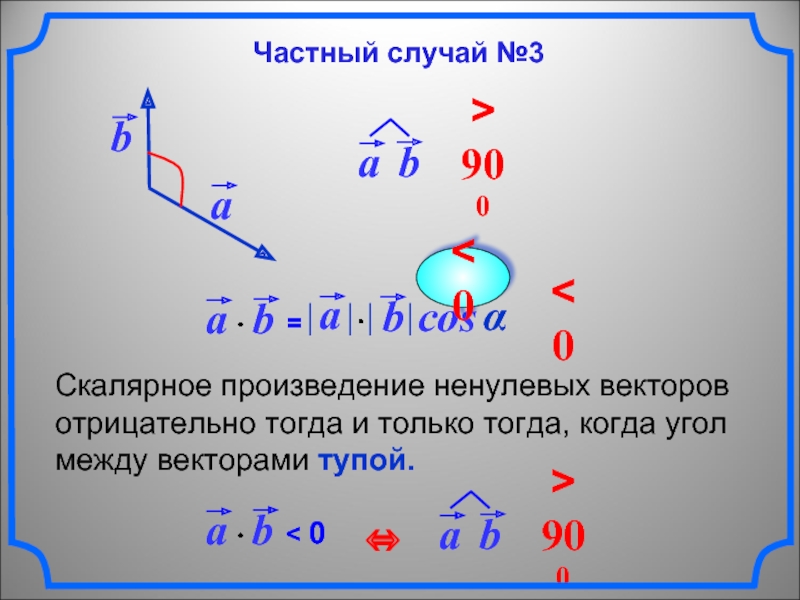
Скалярное произведение ненулевых векторов отрицательно тогда и только тогда, когда
угол между векторами тупой.
cos
α
< 0
< 0
Частный случай №3
Слайд 9cos
00
1
Таким образом,
скалярный квадрат вектора равен квадрату его длины.
Частный случай №5
2
2
2
2
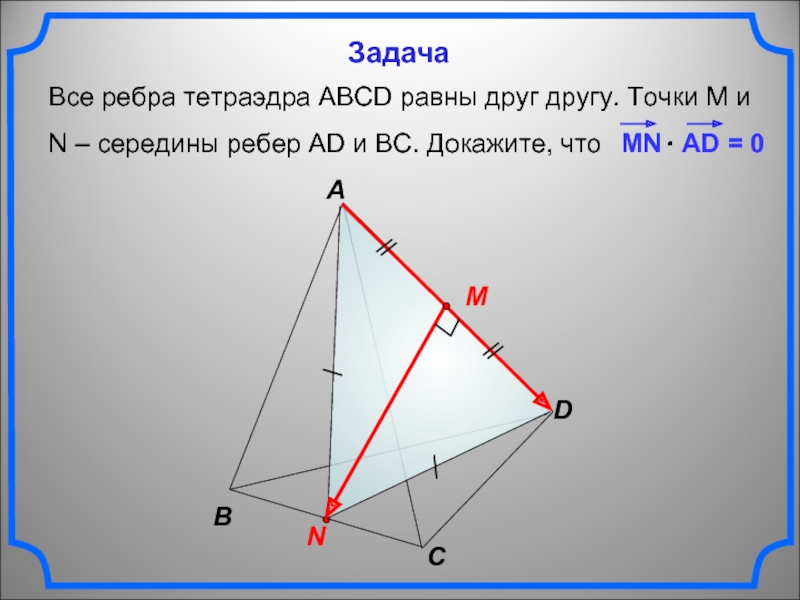
Слайд 10 Все ребра тетраэдра АВСD равны друг другу. Точки М
и
N – середины ребер АD и ВС. Докажите, что
B
C
N
A
D
M
Задача
Слайд 11
Формула для нахождения скалярного произведения
через координаты векторов
= x1x2 + y1y2
+ z1z2
x1x2 + y1y2 + z1z2
Слайд 12Пример №1
Найти скалярное произведение векторов:
a {-6; 9; 5}
b {-1; 0;
7}
x1x2 + y1y2 + z1z2
-6 (-1) + 9 0
+ 5 7 = 41Слайд 13Пример №2
Найти скалярное произведение векторов:
a {0; 0; 4}
b {22; 1;
8}
x1x2 + y1y2 + z1z2
0 22 + 0 1
+ 4 8 = 32Слайд 14Пример №3
Найти скалярное произведение векторов:
a {1; 7; 9}
b {-2; 4;
0}
x1x2 + y1y2 + z1z2
1 (-2) + 7 4
+ 9 0 = 26Слайд 21Проверочная работа
1. Найти скалярное произведение векторов:
a {1; 10; 7}
b {0;
7; 0}
10 7 = 70
Слайд 22Проверочная работа
2. Найти скалярное произведение векторов:
a {7; 25; 0}
b {11;
0; 54}
7 11 = 77
Слайд 23Проверочная работа
3. Найти скалярное произведение векторов:
a {|-2|; 0; |3|}
b {1;
|-11|; 1}
2 1 + 3 1 = 5
Слайд 24Проверочная работа
4. Найти скалярное произведение векторов:
a {sin(900); 2; 3}
b {3;
2; 1}
1 3 + 2 2 + 3 1
= 10Слайд 25Проверочная работа
5. Найти скалярное произведение векторов:
a {-1; 2; 8}
b {5;
5; 0}
-1 5 + 2 5 = 5
Теги