Свойство биссектрисы угла треугольника

Р Е М А
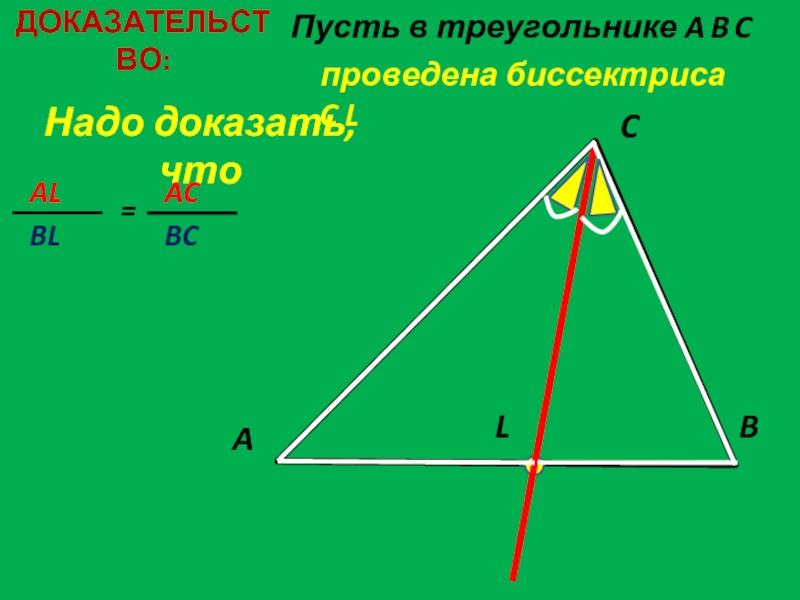
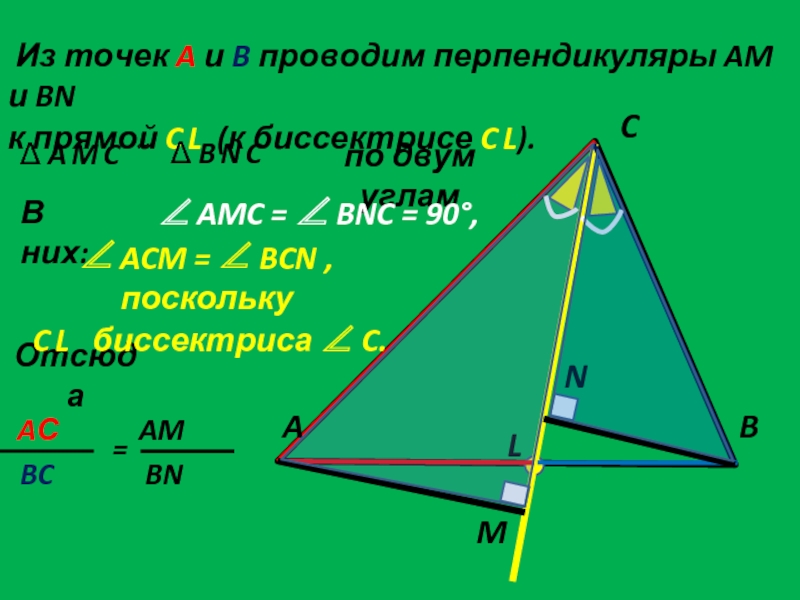
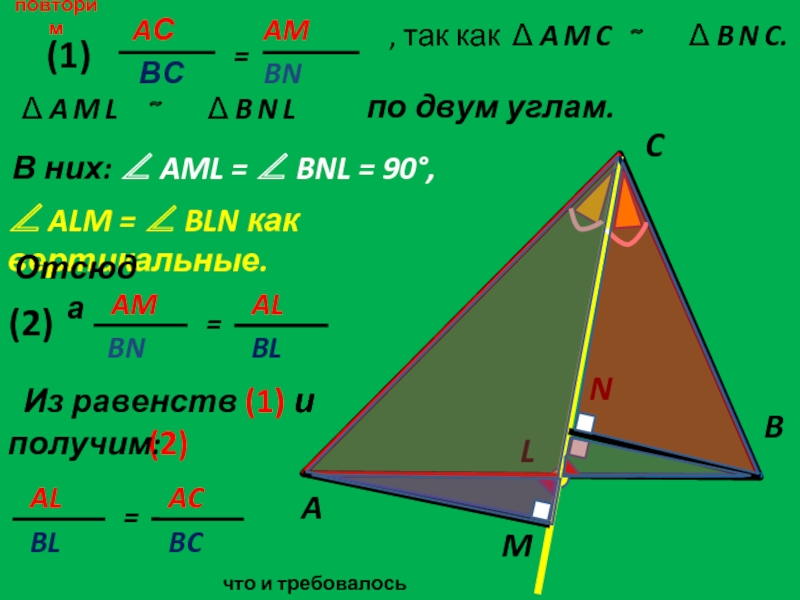
СВОЙСТВО БИССЕКТРИСЫ ТРЕУГОЛЬНИКА
ДЕЛИТ ПРОТИВОЛЕЖАЩУЮ СТОРОНУ НА

ПРОПОРЦИОНАЛЬНЫЕ ПРИЛЕЖАЩИМ СТОРОНАМ

БИССЕКТРИСА УГЛА ТРЕУГОЛЬНИКА

что
A
C
B
L
проведена биссектриса C L

BN к прямой C L (к биссектрисе C L).
по двум

A

C

B

L

M

N

Δ A M C

Δ B N C

 AMC =  BNC = 90°,

Отсюда

 ACM =  BCN , поскольку C L биссектриса  C.

В них:



=  BLN как вертикальные.
Отсюда
Δ A M L
Δ

(1)

(2)

Из равенств (1) и (2)

получим:

В них:  AML =  BNL = 90°,

Δ A M C





что и требовалось доказать.