Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Фалеса
Содержание
- 1. Теорема Фалеса
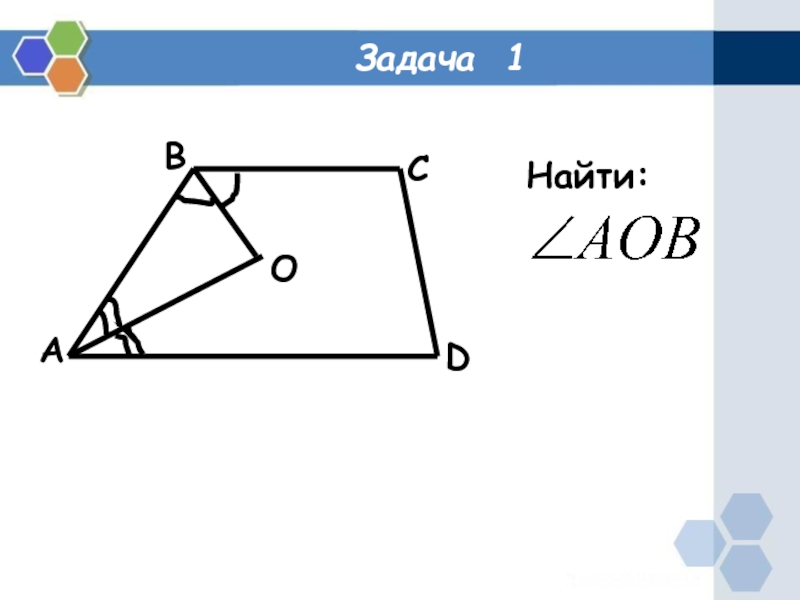
- 2. Задача 1ABDCOНайти:
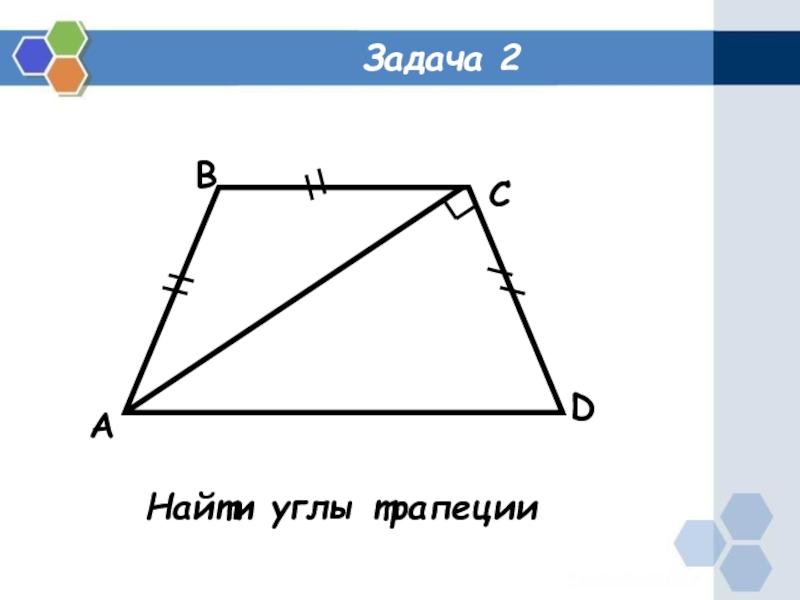
- 3. Задача 2ABCDНайти углы трапеции
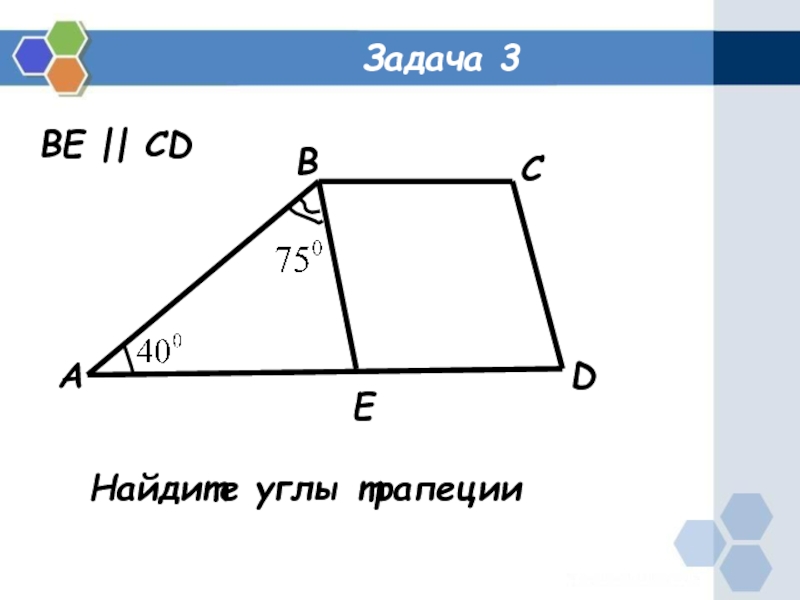
- 4. Задача 3АBCDEBE || CDНайдите углы трапеции
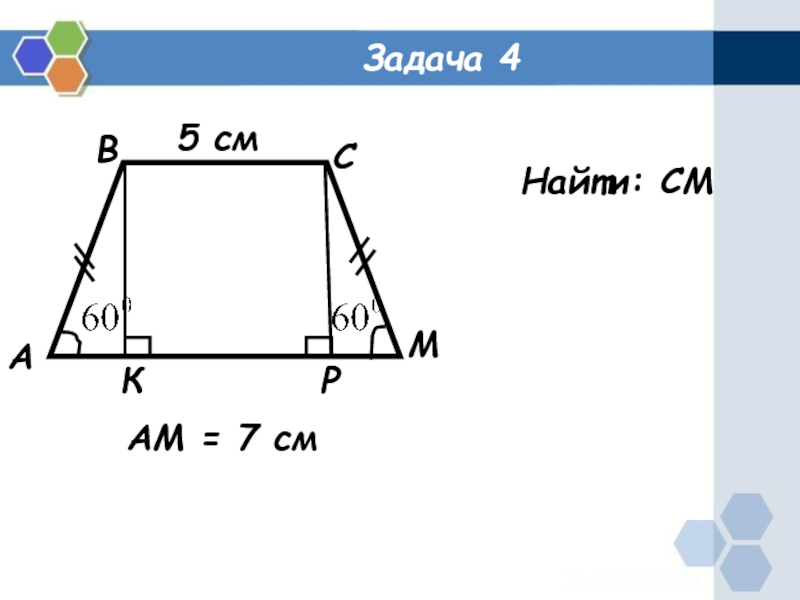
- 5. Задача 4АВСМРК5 смАМ = 7 смНайти: СМ
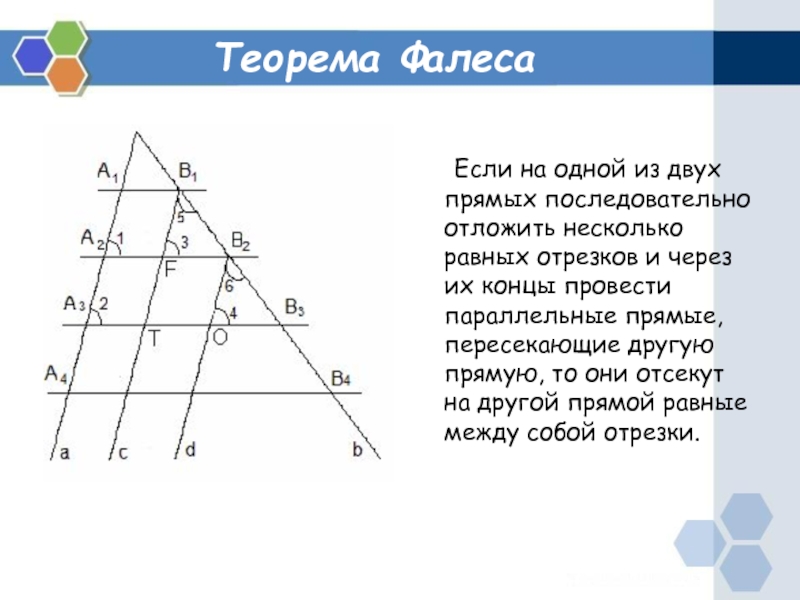
- 6. Теорема Фалеса Если на одной из двух прямых
- 7. Задача (деление отрезка на n равных частей)При
- 8. Средняя линия треугольникаСредней линией треугольника называется отрезок,
- 9. Признак средней линииЕсли отрезок параллелен стороне треугольника,
- 10. Свойства средней линии Дано: ABC – треугольник, ОЄBC,
- 11. Домашняя работа№ 391, 392№ 385 выучить как теоремуПринести циркуль.
- 12. Скачать презентанцию
Задача 1ABDCOНайти:
Слайды и текст этой презентации
Слайд 7Задача (деление отрезка на n равных частей)
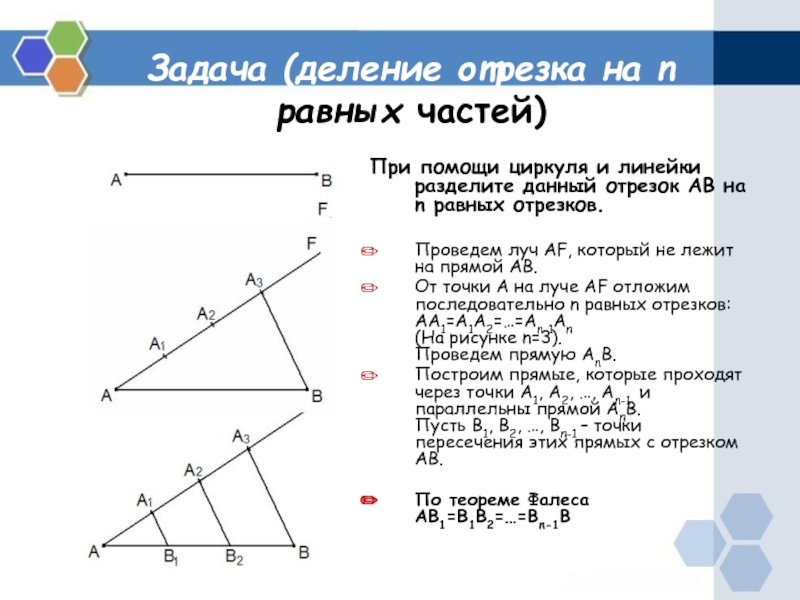
При помощи циркуля и
линейки разделите данный отрезок AB на n равных отрезков.
Проведем луч
AF, который не лежит на прямой AB.От точки A на луче AF отложим последовательно n равных отрезков: AA1=A1A2=…=An-1An (На рисунке n=3). Проведем прямую AnB.
Построим прямые, которые проходят через точки A1, A2, …, An-1 и параллельны прямой AnВ. Пусть B1, B2, …, Bn-1 – точки пересечения этих прямых с отрезком AB.
По теореме Фалеса AB1=B1B2=…=Bn-1B
Слайд 8Средняя линия треугольника
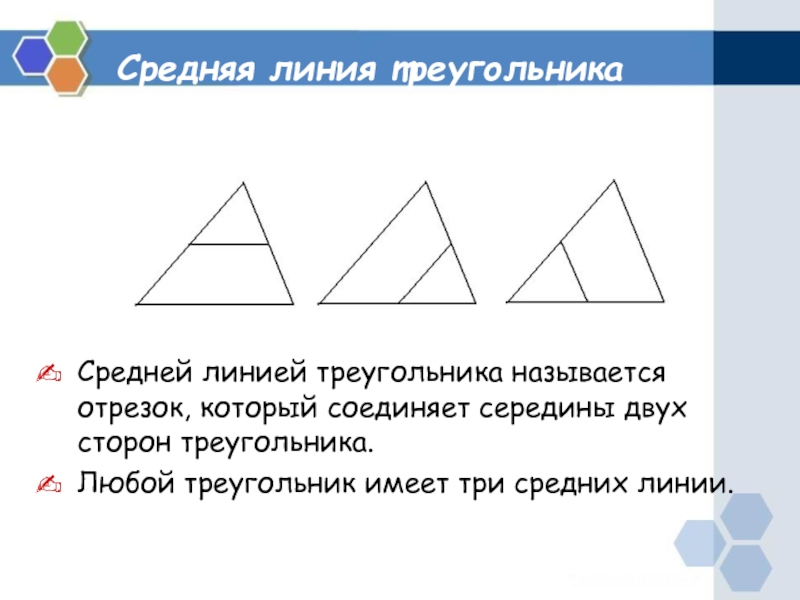
Средней линией треугольника называется отрезок, который соединяет середины
двух сторон треугольника.
Любой треугольник имеет три средних линии.
Слайд 9Признак средней линии
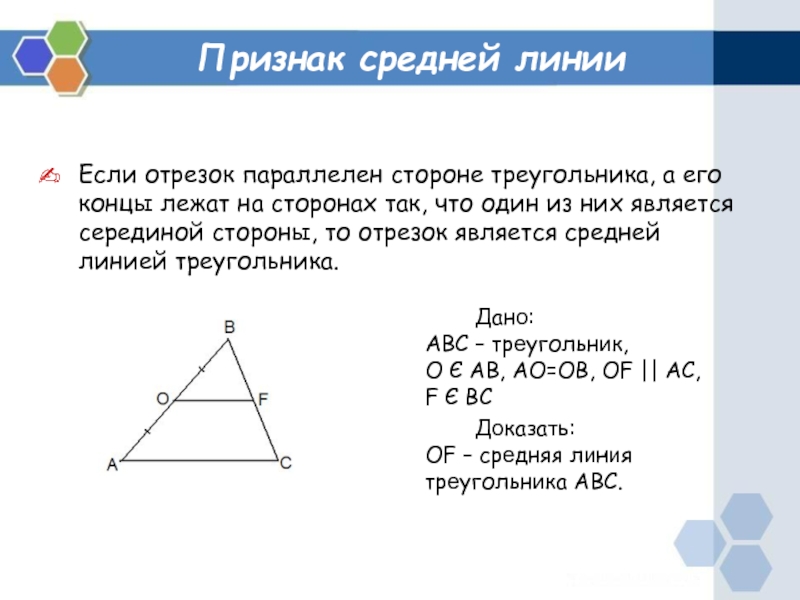
Если отрезок параллелен стороне треугольника, а его концы
лежат на сторонах так, что один из них является серединой
стороны, то отрезок является средней линией треугольника. Дано:
ABC – треугольник,
О Є AB, AO=OB, OF || AC,
F Є BC
Доказать:
OF – средняя линия треугольника ABC.
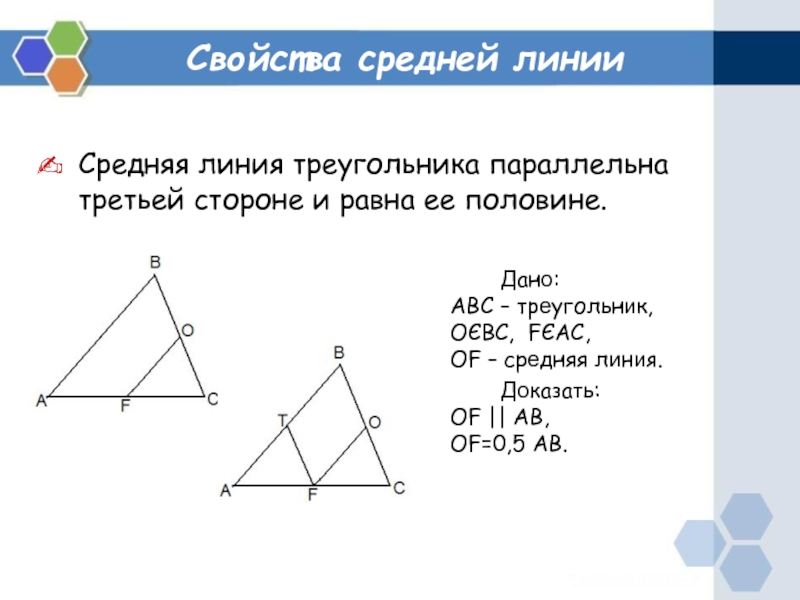
Слайд 10Свойства средней линии
Дано:
ABC – треугольник,
ОЄBC, FЄAC,
OF – средняя линия.
Доказать:
OF ||
AB,
OF=0,5 AB.
Средняя линия треугольника параллельна третьей стороне и равна ее
половине.
Теги