Слайд 1Теорема Пифагора
Различные формулировки
Слайд 2Как известно…
Теорема Пифагора звучит так: «В прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов его катетов», но…
Как звучала эта теорема у
Евклида: «В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол »
Как звучала у Аннаирици: «Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол»
Слайд 3Научное открытие
В настоящее время известно, что эта теорема не была
открыта Пифагором. Однако одни полагают, что Пифатор первым дал ее
полноценное докзательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал". С другой стороны, Прокл утверждает, что доказательство в "Началах" принадлежит самому Евклиду. Как мы видим, история математики почти не сохранила достоверных данных о жизни Пифагора и его математической деятельности. Зато легенда сообщает даже ближайшие обстоятельства, сопровождавшие открытие теоремы. Многим известен сонет Шамиссо:
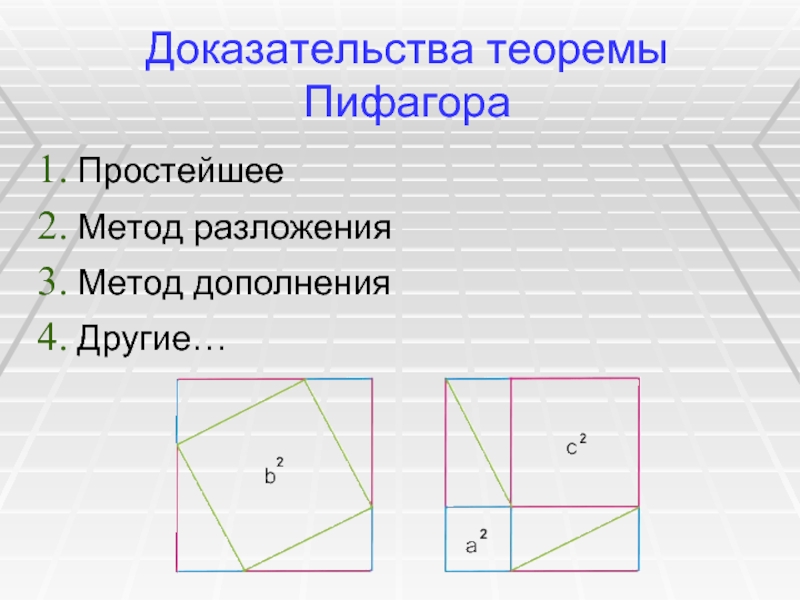
Слайд 4Доказательства теоремы Пифагора
Простейшее
Метод разложения
Метод дополнения
Другие…
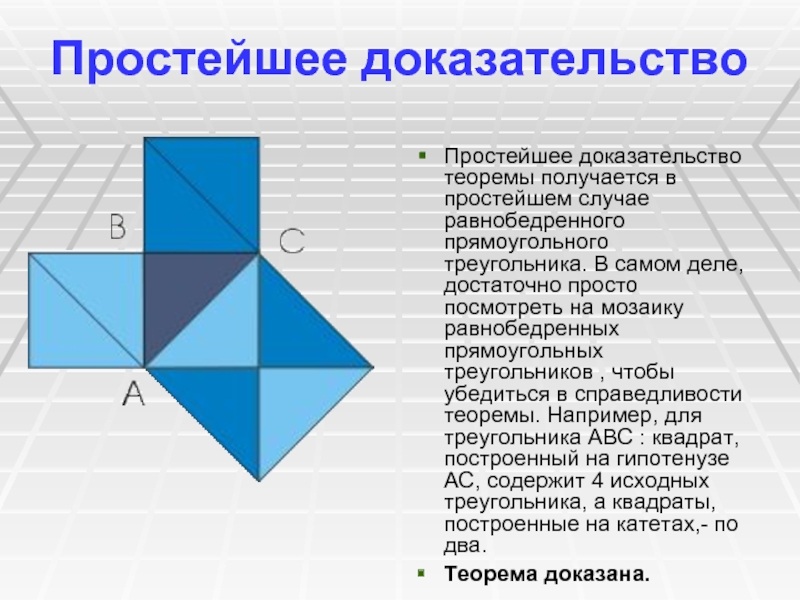
Слайд 5Простейшее доказательство
Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного
треугольника. В самом деле, достаточно просто посмотреть на мозаику равнобедренных
прямоугольных треугольников , чтобы убедиться в справедливости теоремы. Например, для треугольника ABC : квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,- по два.
Теорема доказана.
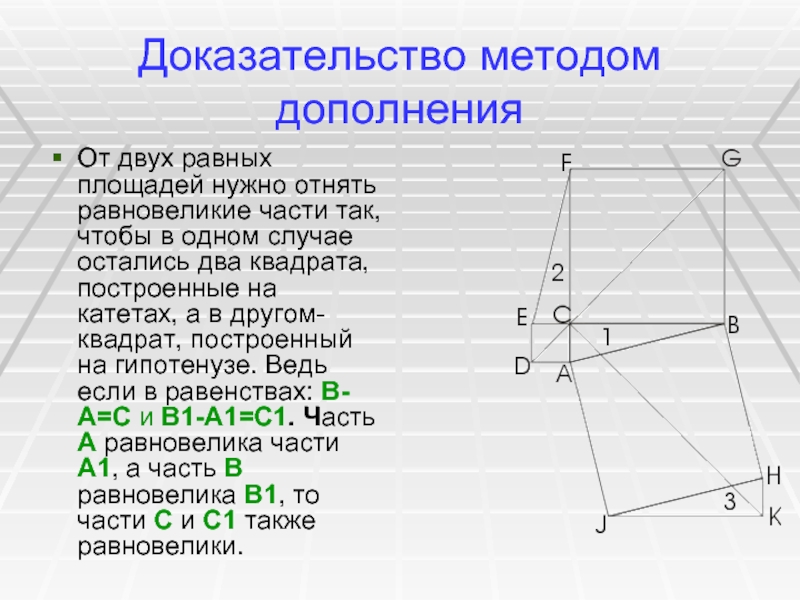
Слайд 6Доказательство методом дополнения
От двух равных площадей нужно отнять равновеликие части
так, чтобы в одном случае остались два квадрата, построенные на
катетах, а в другом- квадрат, построенный на гипотенузе. Ведь если в равенствах: В-А=С и В1-А1=С1. Часть А равновелика части А1, а часть В равновелика В1, то части С и С1 также равновелики.
Слайд 7Доказательство методом дополнения
Поясним этот метод на примере. На рис. к
обычной пифагоровой фигуре приставлены сверху и снизу треугольники 2 и
3, равные исходному треугольнику 1. Прямая DG обязательно пройдет через C. Заметим теперь (далее мы это докажем), что шестиугольники DABGFE и CAJKHB равновелики. Если мы от первого из них отнимем треугольники 1 и 2, то останутся квадраты, построенные на катетах, а если от второго шестиугольника отнимем равные треугольники 1 и 3, то останется квадрат, построенный на гипотенузе. Отсюда вытекает, что квадрат, построенный на гипотенузе, равновелик сумме квадратов,построенных на катетах.
Слайд 8Доказательство методом дополнения
Остается доказать, что наши шестиугольники равновелики. Заметим, что
прямая DG делит верхний шестиугольник на равновеликие части; то же
можно сказать о прямой CK и нижнем шестиугольнике. Повернем четырехугольник DABG, составляющий половину шестиугольника DABGFE, вокруг точки А по часовой стрелке на угол 90; тогда он совпадет с четырехугольником CAJK, составляющим половину шестиугольника CAJKHB. Поэтому шестиугольники DABGFE и CAJKHB равновелики.
Теорема доказана
Слайд 9Доказательство методом вычитания
Знакомый нам чертеж теоремы Пифагора заключим в
прямоугольную рамку, направления сторон которой совпадают с направлениями катетов треугольника.
Продолжим некоторые из отрезков фигуры так, как указано на рисунке, при этом прямоугольник распадается на несколько треугольников, прямоугольников и квадратов. Выбросим из прямоугольника сначала несколько частей так чтобы остался лишь квадрат, построенный на гипотенузе. Эти части следующие:
Слайд 10Доказательство методом вычитания
треугольники 1, 2, 3, 4;
прямоугольник 5;
прямоугольник
6 и квадрат 8;
прямоугольник 7 и квадрат 9;
Затем
выбросим из прямоугольника части так, чтобы остались только квадраты, построенные на катетах. Этими частями будут:
прямоугольники 6 и 7;
прямоугольник 5;
прямоугольник 1(заштрихован);
прямоугольник 2(заштрихован);
Слайд 11Доказательство методом вычитания
Нам осталось лишь показать, что отнятые части равновелики.
Это легко видеть в силу расположения фигур. Из рисунка ясно,
что:
прямоугольник 5 равновелик самому себе;
четыре треугольника 1,2,3,4 равновелики двум прямоугольникам 6 и 7;
прямоугольник 6 и квадрат 8, взятые вместе, равновелики прямоугольнику 1 (заштрихован);;
прямоугольник 7 вместе с квадратом 9 равновелики прямоугольнику 2(заштрихован);
Доказательство закончено
Слайд 12Доказательство Хоукинсa
Прямоугольный треугольник ABC с прямым углом C повернем
на 90° так, чтобы он занял положение A'CB'. Продолжим гипотенузу
A'В' за точку A' до пересечения с линией АВ в точке D. Отрезок В'D будет высотой треугольника В'АВ. Рассмотрим теперь заштрихованный четырехугольник A'АВ'В . Его можно разложить на два равнобедренных треугольника САA' и СВВ' (или на два треугольника A'В'А и A'В'В).
Слайд 13Доказательство Хоукинсa
SCAA'=b²/2, SCBB'=a²/2
SA'AB'B=(a²+b²)/2
Треугольники A'В'А и A'В'В имеют общее основание с
и высоты DA
и DB, поэтому :
SA'AB'B=c*DA/2+ c*DB/2=c(DA+DB)/2=c²/2
Сравнивая два полученных выражения
для площади, получим:
a²+b²=c²
Теорема доказана.
Слайд 14Векторное доказательство
Пусть АВС - прямоугольный треугольник с прямым углом при
вершине С, построенный на векторах. Тогда справедливо векторное равенство:b+c=a
откуда имеем
c = a - b
возводя
обе части в квадрат, получим
c²=a²+b²-2ab
Так как a перпендикулярно b, то ab=0, откуда
c²=a²+b² или c²=a²+b²
Нами снова доказана теорема Пифагора.
Если треугольник АВС - произвольный, то та же формула дает т. н. теорему косинусов, обобщающую теорему Пифагора.
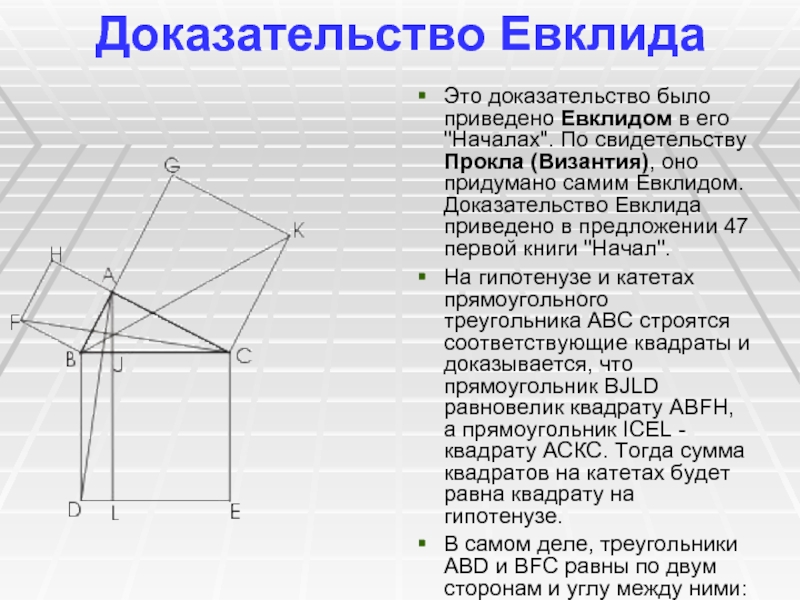
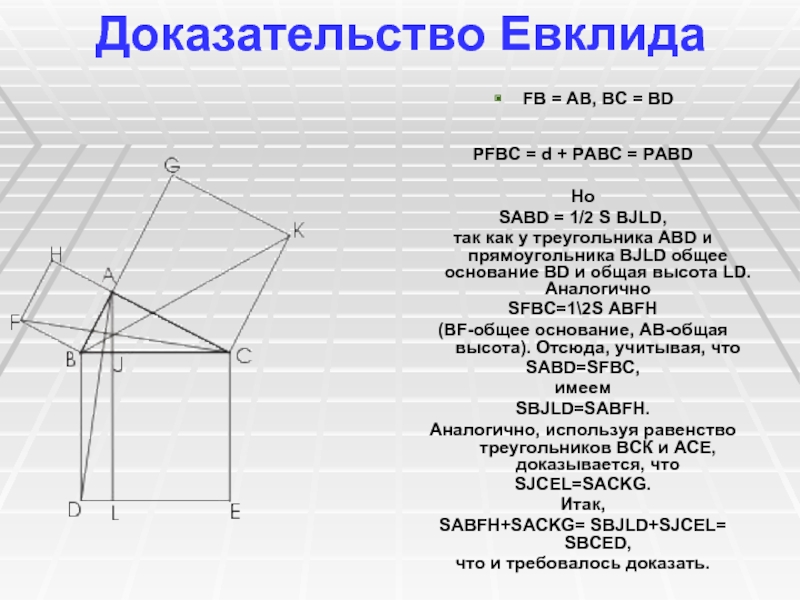
Слайд 15Доказательство Евклида
Это доказательство было приведено Евклидом в его "Началах".
По свидетельству Прокла (Византия), оно придумано самим Евклидом. Доказательство Евклида
приведено в предложении 47 первой книги "Начал".
На гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник ICEL - квадрату АСКС. Тогда сумма квадратов на катетах будет равна квадрату на гипотенузе.
В самом деле, треугольники ABD и BFC равны по двум сторонам и углу между ними:
Слайд 16Доказательство Евклида
FB = AB, BC = BD
РFBC = d + РABC = РABD
Но
SABD = 1/2 S BJLD,
так как у треугольника ABD и прямоугольника
BJLD общее основание BD и общая высота LD. Аналогично
SFBC=1\2S
ABFH
(BF-общее основание, АВ-общая высота). Отсюда, учитывая, что
SABD=SFBC,
имеем
SBJLD=SABFH.
Аналогично, используя равенство треугольников ВСК и АСЕ, доказывается, что
SJCEL=SACKG.
Итак,
SABFH+SACKG= SBJLD+SJCEL= SBCED,
что и требовалось доказать.
Слайд 17Удивительный факт
Вопрос о том, можно ли с помощью световых сигналов
объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией
наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора.
Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.
Слайд 18Итоги работы
На самом деле существует много способов доказательства теоремы Пифагора:
доказательство Евклида, Хоукинса, Вальдхейма, способ «луночками» Гиппократа, доказательство Басхары, Эпштейна,
Нильсена, Бетхера, Перигаля, Гутхейля, векторное доказательство и многие другие…