Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы и их применение при доказательстве задач 8 класс
Содержание
- 1. Векторы и их применение при доказательстве задач 8 класс
- 2. Цели и задачи презентации: -
- 3. Интерес к векторам и векторному исчислению пробудился
- 4. В Древней Греции пифагорейцы, открыв иррациональные числа,
- 5. Математики того времени попытались свести вопросы арифметики
- 6. В геометрическом исчислении, изложенном в труде Евклида
- 7. Фламандский ученый С. Стевин в своем трактате
- 8. Продолжительное время вектор рассматривался только как направленный
- 9. Вектором называется направленный отрезок, для которого
- 10. Отдельные точки плоскости, пространства удобно считать так
- 11. 1) Векторы можно записать двумя большими латинскими
- 12. Длиной или модулем ненулевого вектора называется длина
- 13. Два вектора называются коллинеарными, если они лежат
- 14. Сложение векторов по правилу треугольников
- 15. Сложение векторов по правилу параллелограмма.
- 16. Сумма нескольких векторов. Сложение нескольких векторов производится
- 17. Вычитание векторов.
- 18. Произведение вектора на число Произведением ненулевого вектора
- 19. Скалярное произведение векторов
- 20. Слайд 20
- 21. .
- 22. Слайд 22
- 23. Слайд 23
- 24. Используемая литература и ссылкиhttp://s_ob.mos.edu54.ru/p5aa1… http://slalomum.ru/zakachay/ba… www.budivelne.info/logs »
- 25. Скачать презентанцию
Цели и задачи презентации: - познакомиться с историей возникновения векторов; - повторить основные понятия и действия над векторами; - рассмотреть доказательство теорем векторным методом.
Слайды и текст этой презентации
Слайд 2Цели и задачи презентации: - познакомиться с историей возникновения векторов; - повторить
основные понятия и действия над векторами; - рассмотреть доказательство теорем векторным
методом.Слайд 3Интерес к векторам и векторному исчислению пробудился у математиков в
XIX. в. в связи с потребностями механики и физики. Впервые
вектора были введены в работах У. Гамильтона и Г. Гроссмана. Однако исток и исчисления с направленными отрезками возникли в далеком прошлом.Слайд 4В Древней Греции пифагорейцы, открыв иррациональные числа, которые нельзя выразить
дробями (например: , и др.), не решились ввести
более широкое толкование числа.Слайд 5Математики того времени попытались свести вопросы арифметики и алгебры к
решению задач геометрическим путем. Таким образом, было положено начало геометрической
теории отношений Евдокса (408 – 355 гг. до н.э.), а позднее «геометрической алгебре».Слайд 6В геометрическом исчислении, изложенном в труде Евклида «Начала», сложение и
вычитание сводились к сложению и вычитанию отрезков, а умножение –
к построению прямоугольников на отрезках, соответствующих по длине множителям.Слайд 7Фламандский ученый С. Стевин в своем трактате «Начала статики» рассматривая
сложение сил, приходит к выводу, что для нахождения результата сложения
двух сил, действующих под углом 90˚, необходимо воспользоваться «параллелограммом сил», при этом для обозначения сил он ввел стрелки.Слайд 8Продолжительное время вектор рассматривался только как направленный отрезок, один из
концов которого называли началом, а второй – его концом. С
разработкой теории преобразований вектор стали рассматривать не только как направленный отрезок, но и как параллельный перенос, заданный парой точек – точкой О и ее образом Оʹ.Слайд 9 Вектором называется направленный отрезок, для которого указано его начало и конец: В данном
случае началом отрезка является точка А , концом отрезка – точка
В . Сам вектор обозначен через . Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор , и это уже совершенно другой векторСлайд 10Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором .
У такого вектора конец и начало совпадают.
Слайд 111) Векторы можно записать двумя большими латинскими буквами: и так
далее. При этом первая буква обязательно обозначает точку - начало вектора, а
вторая буква точку - конец вектора. 2) Векторы также записывают маленькими латинскими буквами: В частности, вектор можно для краткости переобозначить маленькой латинской буквой .Слайд 12Длиной или модулем ненулевого вектора называется длина отрезка АВ. Длина
нулевого вектора равна нулю. Длина вектора обозначается знаком модуля:
, В аналитической геометрии рассматривается свободный вектор. Это – вектор, который можно отложить от любой точки:Слайд 13 Два вектора называются коллинеарными, если они лежат на одной прямой
или на параллельных прямых. Если два ненулевых вектора
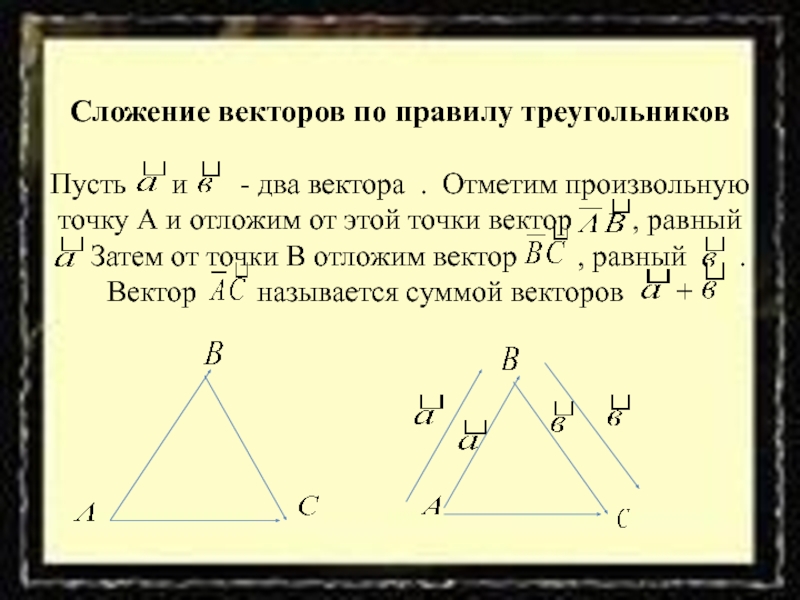
и коллинеарны, то они могут быть направлены либо одинаково, либо противоположно. В первом случае векторы и называются сонаправленными , а во втором – противоположно направленными .Слайд 14 Сложение векторов по правилу треугольников Пусть и
- два вектора . Отметим произвольную точку А и
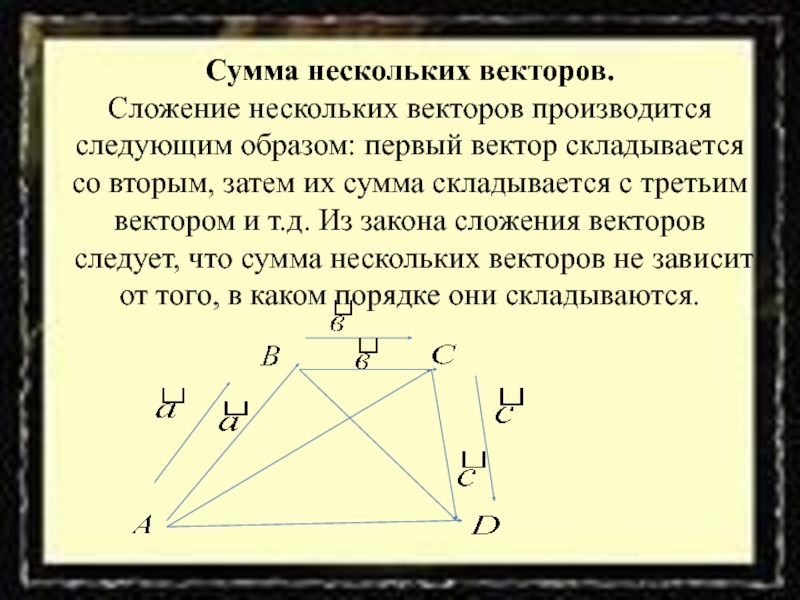
отложим от этой точки вектор , равный . Затем от точки В отложим вектор , равный . Вектор называется суммой векторов +Слайд 16Сумма нескольких векторов. Сложение нескольких векторов производится следующим образом: первый вектор
складывается со вторым, затем их сумма складывается с третьим вектором
и т.д. Из закона сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.Слайд 18Произведение вектора на число Произведением ненулевого вектора на число является
такой вектор , длина которого равна
, причём векторы и сонаправлены при и противоположно направлены при . Произведением нулевого вектора на любое число считается нулевой вектор.Слайд 24Используемая литература и ссылки
http://s_ob.mos.edu54.ru/p5aa1…
http://slalomum.ru/zakachay/ba…
www.budivelne.info/logs » Шаблоны для школьных презентаций
http://www.smarttehno.ru/port/… ▼
Геометрия: Учеб. Для
7 – 9 кл. общеобразоват. учреждений/ Л.С. Атанасян, В.Ф. Бутузов,
С.Б. Кадомцев и др. – 6-е изд. – М.: Просвещение, 1996.Глейзер Г. И. История математики в школе в VII – IX кл.: Пособие для учителей. – М.: Просвещение, 1981.
Энциклопедический словарь юного математика/ Сост. Э-68 А. П. Савин. - М.: Педагогика, 1989.