Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок по геометрии для 10 класса "Понятие многогранника. Призма"
Содержание
- 1. Урок по геометрии для 10 класса "Понятие многогранника. Призма"
- 2. Цели урока:ввести понятие многогранника, призмы и их
- 3. Ход урока: Объяснение нового материала
- 4. Многогранник – поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело.ТетраэдрПараллелепипедОктаэдр
- 5. Многоугольники, из которых составлен многогранник, называются его
- 6. Стороны граней называются ребрами, а концы ребер-
- 7. Плоскость, по обе стороны от которой имеются
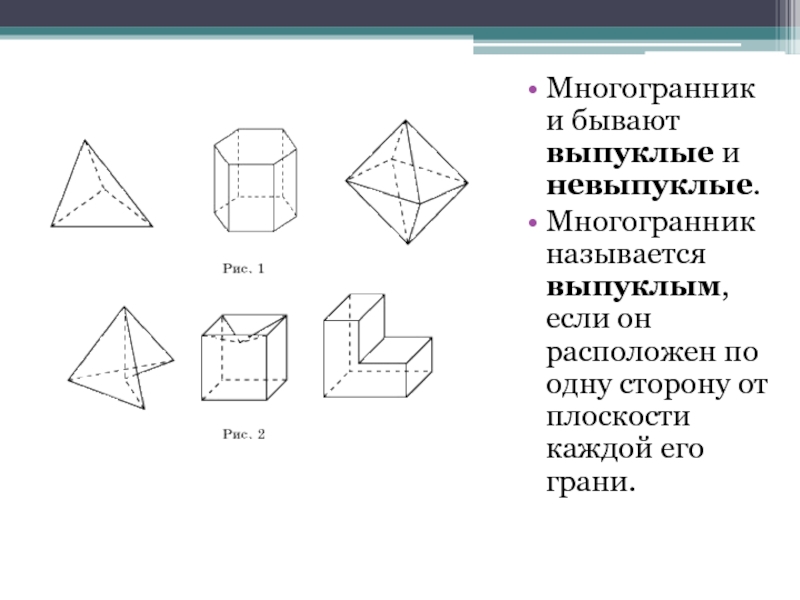
- 8. Многогранники бывают выпуклые и невыпуклые. Многогранник называется
- 9. Многогранник , составленный из двух равных многоугольников
- 10. Многоугольники А1А2…Аn и В1В2…Вn называются основаниями, а
- 11. Перпендикуляр, проведенный из какой-нибудь точки одного основания
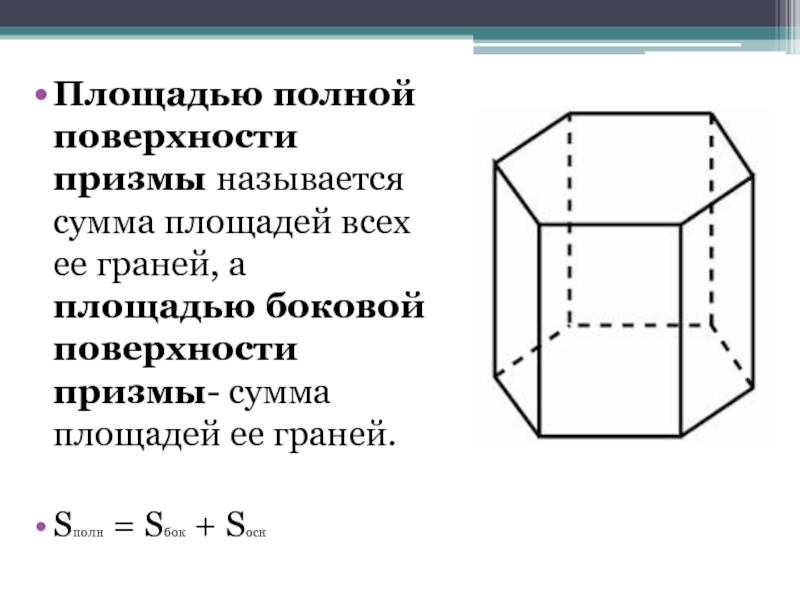
- 12. Площадью полной поверхности призмы называется сумма площадей
- 13. Теорема:Площадь боковой поверхности прямой призмы равна произведению
- 14. Устно: № 218В тетради и на
- 15. П.П. 25-27 учить№№ 220, 229 (б, в), 231Подведение итогов, домашнее задание
- 16. Скачать презентанцию
Цели урока:ввести понятие многогранника, призмы и их элементов;рассмотреть виды призмы, ввести понятие площади поверхности призмы;вывести формулу для вычисления площади поверхности прямой призмы
Слайды и текст этой презентации
Слайд 2Цели урока:
ввести понятие многогранника, призмы и их элементов;
рассмотреть виды призмы,
ввести понятие площади поверхности призмы;
прямой призмыСлайд 4Многогранник – поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое
тело.
Тетраэдр
Параллелепипед
Октаэдр
Слайд 5Многоугольники, из которых составлен многогранник, называются его гранями.
Гранями тетраэдра и
октаэдра являются треугольники. А гранями параллелепипеда- параллелограммы.
Слайд 6Стороны граней называются ребрами, а концы ребер- вершинами многогранника.
Отрезок, соединяющий
две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Слайд 7Плоскость, по обе стороны от которой имеются точки многогранника, называется
секущей плоскостью, а общая часть многогранника и секущей плоскости- сечением
многогранника.Слайд 8Многогранники бывают выпуклые и невыпуклые.
Многогранник называется выпуклым, если он
расположен по одну сторону от плоскости каждой его грани.
Слайд 9Многогранник , составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn,
расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.
Слайд 10Многоугольники А1А2…Аn и В1В2…Вn называются основаниями, а параллелограммы- боковыми гранями
призмы. Отрезки А1В1, А2В2, АnВn называются боковыми ребрами.
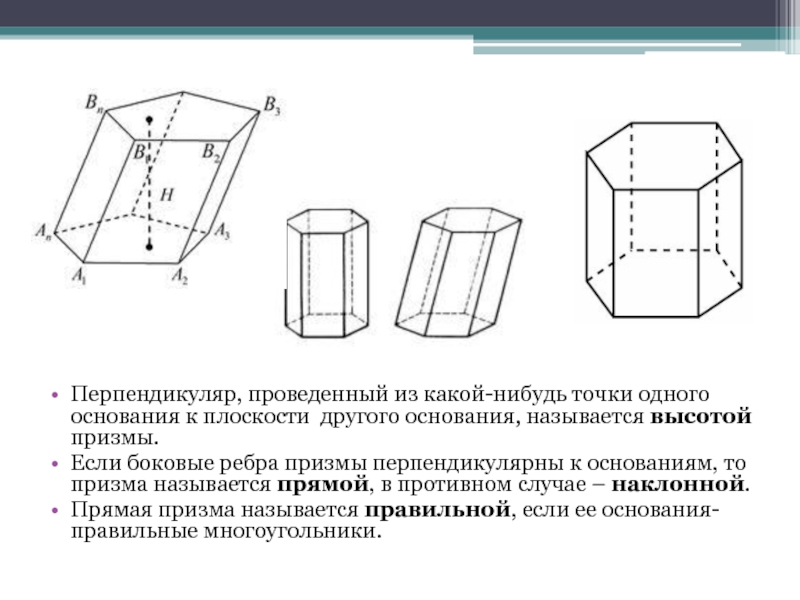
Слайд 11Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого
основания, называется высотой призмы.
Если боковые ребра призмы перпендикулярны к основаниям,
то призма называется прямой, в противном случае – наклонной.Прямая призма называется правильной, если ее основания- правильные многоугольники.