Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи на построение. Строим циркулем и линейкой
Содержание
- 1. Задачи на построение. Строим циркулем и линейкой
- 2. На данном луче от его начала отложить отрезок, равный данному.Задача 1
- 3. ВАИзобразим фигуры, данные в условии задачи: луч ОС и отрезок АВОС
- 4. Затем циркулем построим окружность радиуса АВ с
- 5. Задача 2Отложить от данного луча угол, равный данному.
- 6. Изобразим фигуры: угол А и луч ОММОА
- 7. Проведём окружность произвольного радиуса с центром в
- 8. Затем проведём окружность того же радиуса с
- 9. После этого построим окружность с центром D,
- 10. Рассмотрим треугольники АВС и ОDЕ. Отрезки АВ
- 11. Задача 3Построить биссектрису данного угла.
- 12. Нарисуем угол A и проведём окружность (A;
- 13. Затем проведём две окружности одинакового радиуса ВС
- 14. САВЕДокажем, что луч АЕ является биссектрисой данного
- 15. Дана прямая и точка на ней. Построить
- 16. Дана прямая а и дана точка М, принадлежащая этой прямой.аМ
- 17. На лучах прямой а, исходящих из точки
- 18. Проведём прямую QР через точку М, и
- 19. Задача 5Построить середину данного отрезка.
- 20. Пусть АВ – данный отрезок. Построим две
- 21. ОАВРQ
- 22. ОАВРQ12В самом деле, треугольники АРQ и ВРQ
- 23. Следовательно, отрезок РО – биссектриса равнобедренного треугольника
- 24. Скачать презентанцию
На данном луче от его начала отложить отрезок, равный данному.Задача 1
Слайды и текст этой презентации
Слайд 1Задачи на построение.
Строим циркулем и линейкой!
Автор: Наумов Владислав,
ученик МОУ
«Корниловская СОШ».
Двинской Верхнетоемского района Архангельской области
Слайд 4Затем циркулем построим окружность радиуса АВ с центром О. Эта
окружность пересечёт луч ОС в некоторой точке D. Отрезок ОD
–искомый.О
С
D
Слайд 7
Проведём окружность произвольного радиуса с центром в вершине А данного
угла. Эта окружность пересекает стороны угла в точках В и
С.А
С
В
Слайд 8
Затем проведём окружность того же радиуса с центром в начале
данного луча ОМ. Она пересекает луч в точке D.
О
D
М
Слайд 9
После этого построим окружность с центром D, радиус которой равен
ВС. Окружности с центрами О и D пересекаются в двух
точках. Одну из этих точек обозначим буквой Е. Докажем, что угол МОЕ -искомый.Е
О
D
М
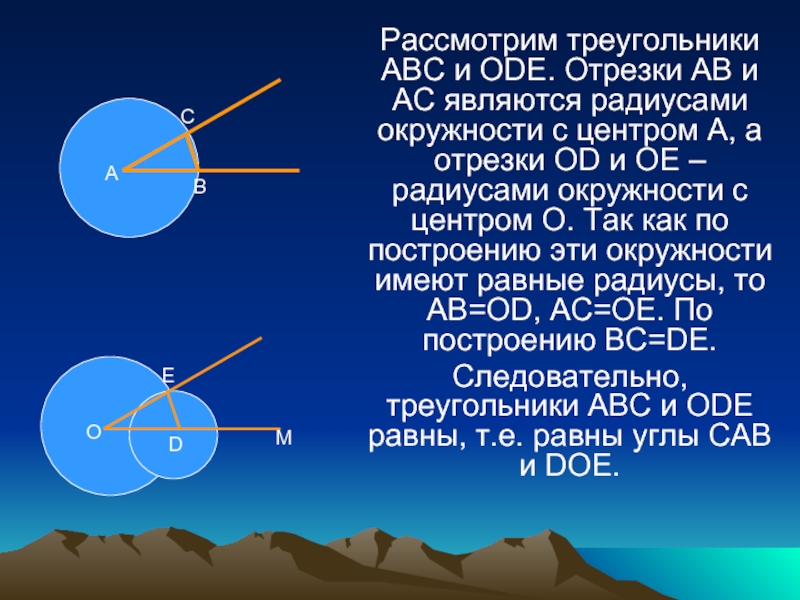
Слайд 10Рассмотрим треугольники АВС и ОDЕ. Отрезки АВ и АС являются
радиусами окружности с центром А, а отрезки ОD и ОЕ
–радиусами окружности с центром О. Так как по построению эти окружности имеют равные радиусы, то АВ=ОD, АС=ОЕ. По построению ВС=DЕ.Следовательно, треугольники АВС и ОDE равны, т.е. равны углы САВ и DOE.
О
Е
D
М
А
С
В
Слайд 12Нарисуем угол A и проведём окружность (A; r) она пересекает
стороны угла в точках В и С.
С
А
В
Слайд 13Затем проведём две окружности одинакового радиуса ВС с центрами в
точках В и С. Они пересекутся в двух точках. Ту
из этих точек, которая лежит внутри угла ВАС, обозначим буквой Е.С
А
В
Е
Слайд 14С
А
В
Е
Докажем, что луч АЕ является биссектрисой данного угла ВАС.
Рассмотрим треугольники
АСЕ и АВЕ. ОНИ равны по трём сторонам. В самом
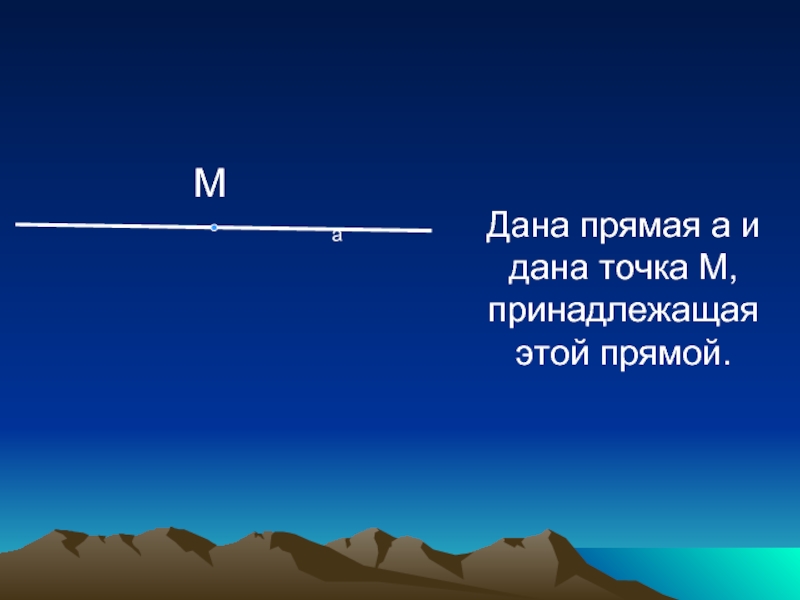
деле, АЕ – общая сторона; АС и АВ равны как радиусы одной и той же окружности; СЕ=ВЕ по построению.
Слайд 15Дана прямая и точка на ней. Построить прямую, проходящую через
данную точку и перпендикулярную к данной прямой.
Задача 4
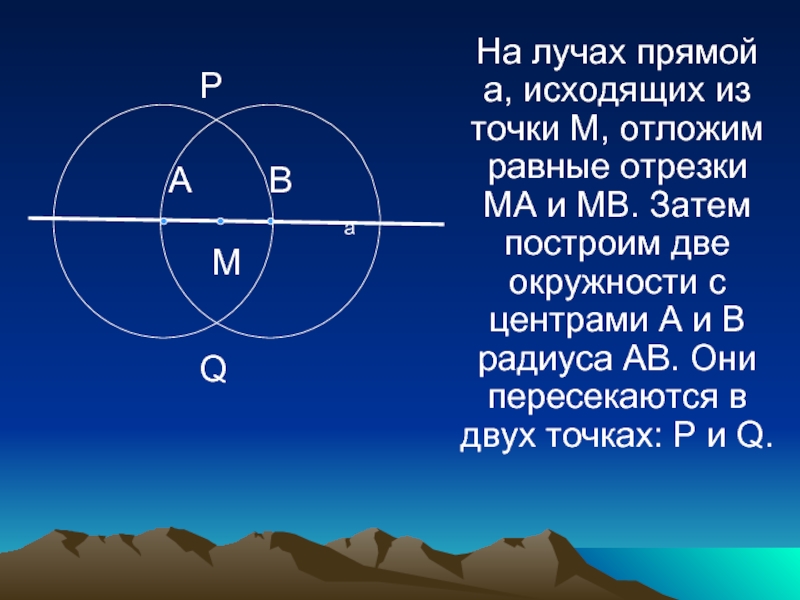
Слайд 17На лучах прямой а, исходящих из точки М, отложим равные
отрезки МА и МВ. Затем построим две окружности с центрами
А и В радиуса АВ. Они пересекаются в двух точках: Р и Q.а
М
А
В
Р
Q
Слайд 18Проведём прямую QР через точку М, и докажем, что эта
прямая – искомая, т. е. что она перпендикулярна к данной
прямой а.В самом деле, так как медиана РМ равнобедренного треугольника РАВ является также высотой, то РМ перпендикулярна а.
а
М
А
В
Р
Q
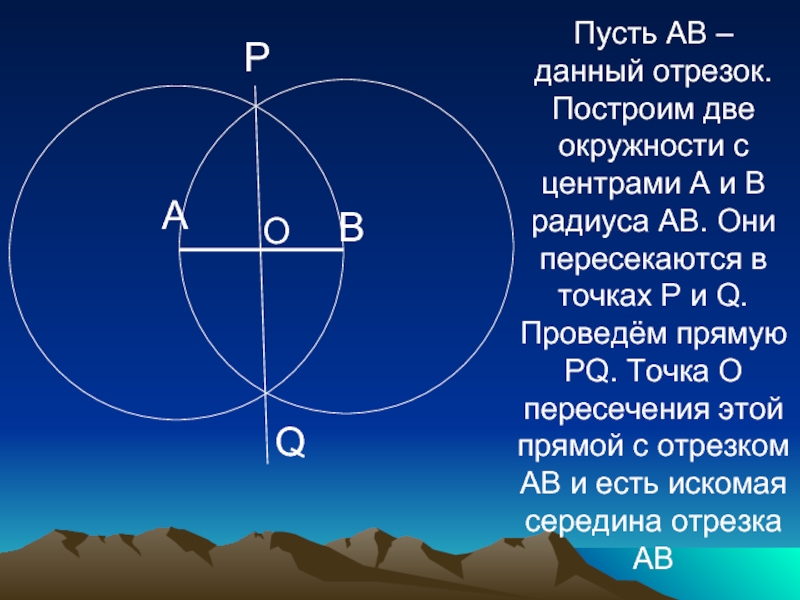
Слайд 20Пусть АВ – данный отрезок. Построим две окружности с центрами
А и В радиуса АВ. Они пересекаются в точках Р
и Q. Проведём прямую РQ. Точка О пересечения этой прямой с отрезком АВ и есть искомая середина отрезка АВО
А
В
Р
Q
Слайд 23Следовательно, отрезок РО – биссектриса равнобедренного треугольника АРВ, а значит,
и медиана, т. е. точка О – середина отрезка АВ.
