Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЕГЭ Теория вероятностей (задание №4.)
Содержание
- 1. ЕГЭ Теория вероятностей (задание №4.)
- 2. Случайным называется событие, которое может либо произойти, либо нет.
- 3. Достоверным называется событие, которое обязательно произойдет.
- 4. Действие, которое может привести к одному из нескольких результатов, в теории вероятностей называют испытанием.
- 5. Вероятность события равна отношению числа благоприятных исходов
- 6. Произведением событий А и В называется событие
- 7. События событий А и В называются независимыми,
- 8. №431. Лена и Саша играют в кости.
- 9. №282853. В случайном эксперименте бросают две
- 10. Слайд 10
- 11. Р(А)=5:36 ≈ 0,14 Ответ: 0,14
- 12. №282855. В чемпионате по гимнастике участвуют
- 13. 1) 20-(7+8)=5 спортсменок из Китая 2)5:20=0,25 Ответ: 0,25
- 14. №282856. В среднем из 1000 садовых
- 15. 1) 1000-5=995 насосов не подтекают 2) 995:1000=0,995 Ответ: 0,995
- 16. №282857. Фабрика выпускает сумки. В среднем
- 17. 1) 100+8=108 общее количество сумок. 2)100:108 ≈ 0,93 Ответ: 0,93
- 18. №282858. В соревнованиях по толканию
- 19. 1) 4+7+9+5=25 общее количество спортсменов 2) 9:25=0,36 Ответ: 0,36
- 20. №285922. Научная конференция проводится в 5
- 21. 1) (75-3∙17):2=12 докладов в 4-ый и 5-ый дни 2) 12:75=0,16 Ответ: 0,16
- 22. №285923 Конкурс исполнителей проводится в 5
- 23. 1) (80-8):4=18 докладов в остальные дни. 2) 18:80=0,225 Ответ: 0,225
- 24. №285924 На семинар приехали 3 ученых
- 25. 1) 3+3+4=10 докладов всего 2) 3:10=0,3 Ответ: 0,3
- 26. №285925 Перед началом первого тура
- 27. 1) 10-1=9 спортсменов из России, кроме Руслана
- 28. №285926 В сборнике билетов по
- 29. 1) 11:55=0,2 Ответ: 0,2
- 30. №285927 В сборнике билетов по математике
- 31. 1) 25-10=15 билетов не содержит вопросов по неравенствам 2) 15:25=0,6 Ответ: 0,6
- 32. №372. Игральную кость (кубик) бросили 1 раз. Какова вероятность того, что выпало менее 4-х очков?
- 33. Менее 4-х очков: 1,2,3. Всего 6 вариантов. 3:6=0,5 Ответ:0,5
- 34. № 381. Перед началом футбольного матча судья
- 35. А={В матче «Меркурий»- «Марс» право владеть мячом
- 36. № 410. Люда дважды бросает игральный кубик.
- 37. Всех исходов 4: 9=3+6 9=4+5 9=5+4 (благоприятный исход) 9=6+3 1:4=0,25 Ответ:0,25
- 38. №431. Лена и Саша играют в кости.
- 39. 2:5=0,4 Ответ:0,4
- 40. Скачать презентанцию
Случайным называется событие, которое может либо произойти, либо нет.
Слайды и текст этой презентации
Слайд 1ЕГЭ
Теория вероятностей
(задание №4.)
Шерина С.А., учитель математики
МБОУ «Борисовская средняя
общеобразовательная школа».
Слайд 4Действие, которое может привести к одному из нескольких результатов, в теории вероятностей называют
испытанием.
Слайд 5Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.
Р(А)=
Слайд 6Произведением событий А и В называется событие АВ, которое наступает
тогда и только тогда, когда наступают оба события: А и
В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.
Слайд 7События событий А и В называются независимыми, если появление одного
из них не меняет вероятности появления другого. Теорема об умножении
вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле: Р(АВ)=Р(А)∙Р(В)
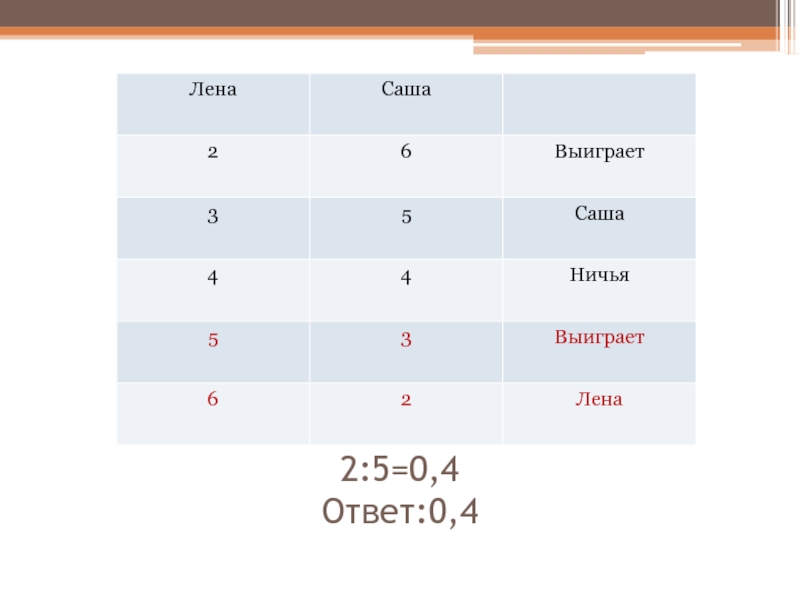
Слайд 8№431. Лена и Саша играют в кости. Они бросают кость по
одному разу. Выигрывает тот, кто выбросил больше очков. Если очков
выпало поровну, то наступает ничья. В сумме выпало 8 очков. Найдите вероятность того, что Лена выиграла.
Слайд 9№282853. В случайном эксперименте бросают две игральные кости. Найдите вероятность
того, что в сумме выпадет 8 очков. Результат округлите до
сотых.
Слайд 12№282855. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из
России, 7 из США, остальные — из Китая. Порядок, в
котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Слайд 14№282856. В среднем из 1000 садовых насосов, поступивших в продажу,
5 подтекают. Найдите вероятность того, что один случайно выбранный для
контроля насос не подтекает.
Слайд 16№282857. Фабрика выпускает сумки. В среднем на 100 качественных сумок
приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что
купленная сумка окажется качественной. Результат округлите до сотых.
Слайд 18 №282858. В соревнованиях по толканию ядра участвуют 4 спортсмена из
Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и
5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Слайд 20№285922. Научная конференция проводится в 5 дней. Всего запланировано 75
докладов — первые три дня по 17 докладов, остальные распределены
поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Слайд 22№285923 Конкурс исполнителей проводится в 5 дней. Всего заявлено 80
выступлений — по одному от каждой страны. В первый день
8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
Слайд 24№285924 На семинар приехали 3 ученых из Норвегии, 3 из
России и 4 из Испании. Порядок докладов определяется жеребьёвкой. Найдите
вероятность того, что восьмым окажется доклад ученого из России.
Слайд 26 №285925 Перед началом первого тура чемпионата по бадминтону участников разбивают
на игровые пары случайным образом с помощью жребия. Всего в
чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
Слайд 271) 10-1=9 спортсменов из России, кроме Руслана Орлова. 2)26-1=25 всего спортсменов,
кроме Руслана Орлова.
3) 9: 25=0,36
Ответ: 0,36
Слайд 28 №285926 В сборнике билетов по биологии всего 55 билетов, в
11 из них встречается вопрос по ботанике. Найдите вероятность того,
что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике.
Слайд 30№285927 В сборнике билетов по математике всего 25 билетов, в
10 из них встречается вопрос по неравенствам. Найдите вероятность того,
что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.
Слайд 32№372. Игральную кость (кубик) бросили 1 раз. Какова вероятность того, что
выпало менее 4-х очков?
Слайд 34№ 381. Перед началом футбольного матча судья бросает монету, чтобы определить,
какая из команд будет первая владеть мячом. Команда «Меркурий» по
очереди играет с командами «Марс», «Юпитер» и «Уран». Найдите вероятность того, что во всех матчах право владеть мячом выигрывает команда «Меркурий».
Слайд 35А={В матче «Меркурий»- «Марс» право владеть мячом выигрывает команда «Меркурий»}. В={В
матче «Меркурий»- «Юпитер» право владеть мячом выигрывает команда «Меркурий»}. С={В матче
«Меркурий»- «Уран» право владеть мячом выигрывает команда «Меркурий»}. Р(АВС)=0,5 ∙0,5 ∙0,5=0,125 Ответ: 0,125
Слайд 36№ 410. Люда дважды бросает игральный кубик. В сумме у неё
выпало 11 очков. Найдите вероятность того, что при первом броске
выпало 6 очков.
Слайд 38№431. Лена и Саша играют в кости. Они бросают кость по
одному разу. Выигрывает тот, кто выбросил больше очков. Если очков
выпало поровну, то наступает ничья. В сумме выпало 8 очков. Найдите вероятность того, что Лена выиграла.
