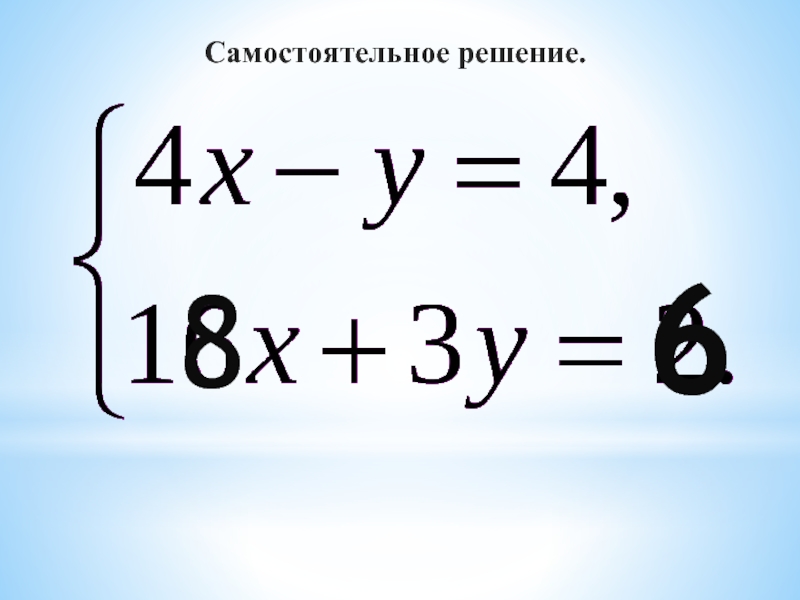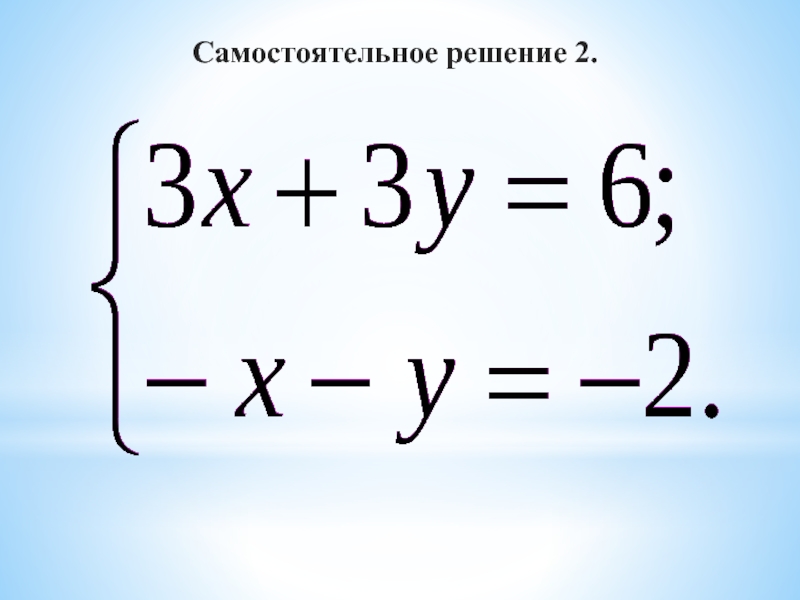Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Графический способ решения линейных систем уравнений
Содержание
- 1. Графический способ решения линейных систем уравнений
- 2. Линейная функция – это функция вида y=kx+b
- 3. Слайд 3
- 4. Система уравнений – это некоторое количество
- 5. 1). Выразить y через x в каждом
- 6. Пусть даны две линейные функции y=k1*x+b1 и
- 7. Взаимное расположение графиков линейных функций
- 8. 2). Если прямые, являющиеся графиками уравнений системы,
- 9. 3). Если прямые, являющиеся графиками уравнений системы, совпадают,
- 10. Пример решения.
- 11. Самостоятельное решение. 86
- 12. Самостоятельное решение 2.
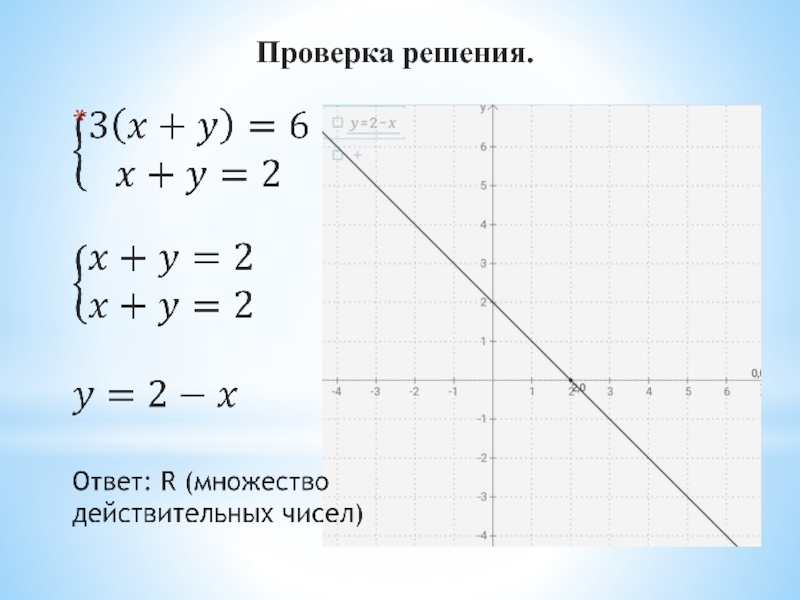
- 13. Проверка решения.
- 14. Все умнички! Спасибо за внимание
- 15. Скачать презентанцию
Линейная функция – это функция вида y=kx+b , в котором k и b - действительные числа. Графиком линейной функции y=kx+b является прямая. Алгоритм построения: 1). Выразить y через x. 2). Прописать название
Слайды и текст этой презентации
Слайд 2Линейная функция – это функция вида y=kx+b , в котором
k и b - действительные числа.
построения: 1). Выразить y через x. 2). Прописать название функции и что является графиком. 3). Составить таблицу значений каждой функции. 4). Построить координатную плоскость. 5).Отметить эти точки на плоскости и провести через них прямую.Слайд 4 Система уравнений – это некоторое количество уравнений, объединённых фигурной
скобкой, которая означает, что все уравнения должны выполняться одновременно.
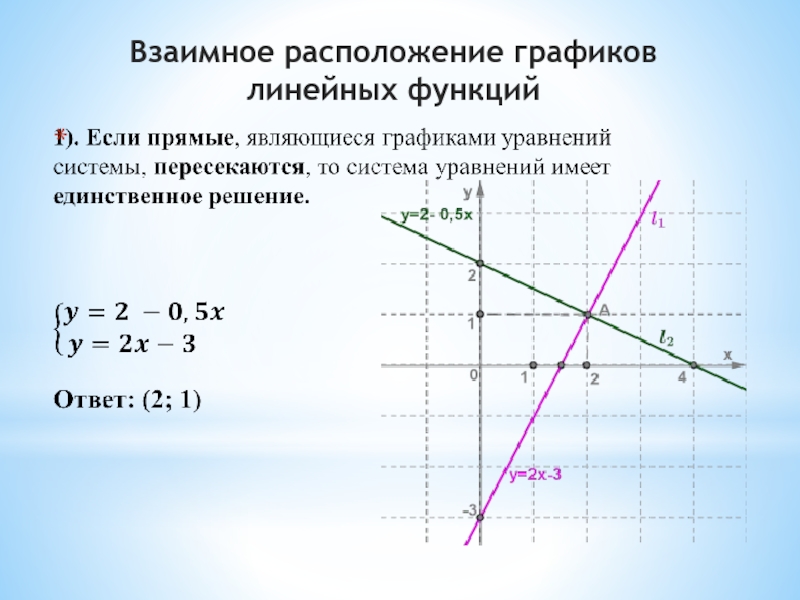
Решить
систему уравнений – это значит
найти все её решения, или доказать, что решений нет. Слайд 51). Выразить y через x в каждом уравнении.
2). Прописать название
функции и что является графиком.
3). Составить таблицу значений каждой функции.
4).
Построить координатную плоскость. 5). Построить в одной системе координат графики функций.
6). Найти точки пересечения графиков.
Алгоритм решения системы уравнений графическим способом
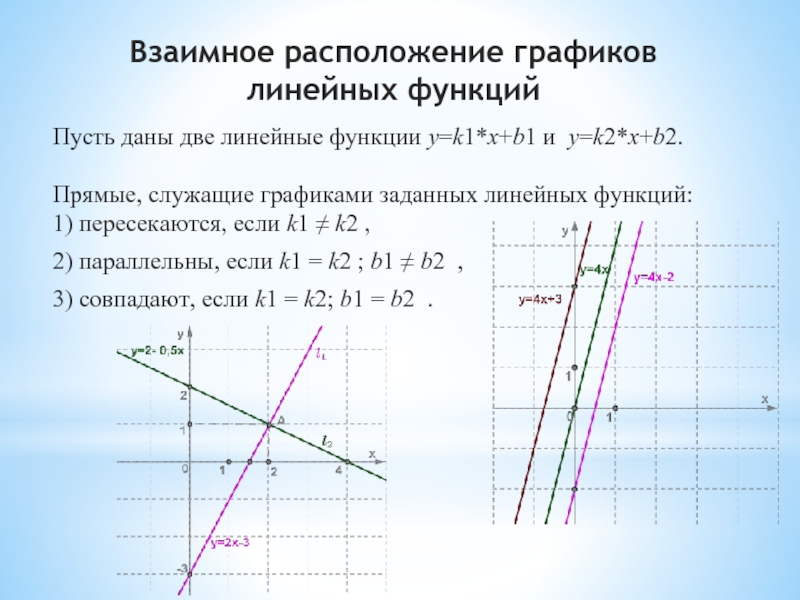
Слайд 6Пусть даны две линейные функции y=k1*x+b1 и y=k2*x+b2. Прямые, служащие графиками
заданных линейных функций:
1) пересекаются, если k1 ≠ k2 ,
2) параллельны,
если k1 = k2 ; b1 ≠ b2 ,3) совпадают, если k1 = k2; b1 = b2 .
Взаимное расположение графиков линейных функций
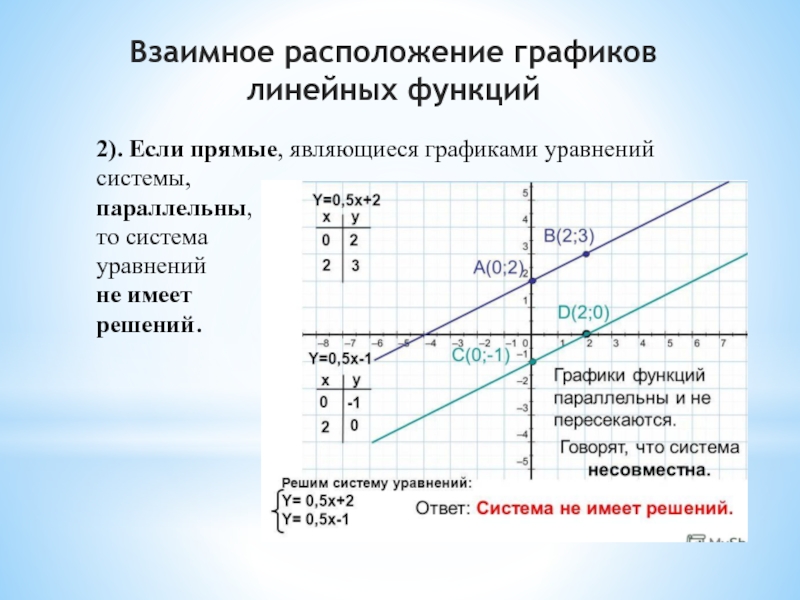
Слайд 82). Если прямые, являющиеся графиками уравнений системы, параллельны, то система уравнений не имеет
решений.
Взаимное расположение графиков линейных функций
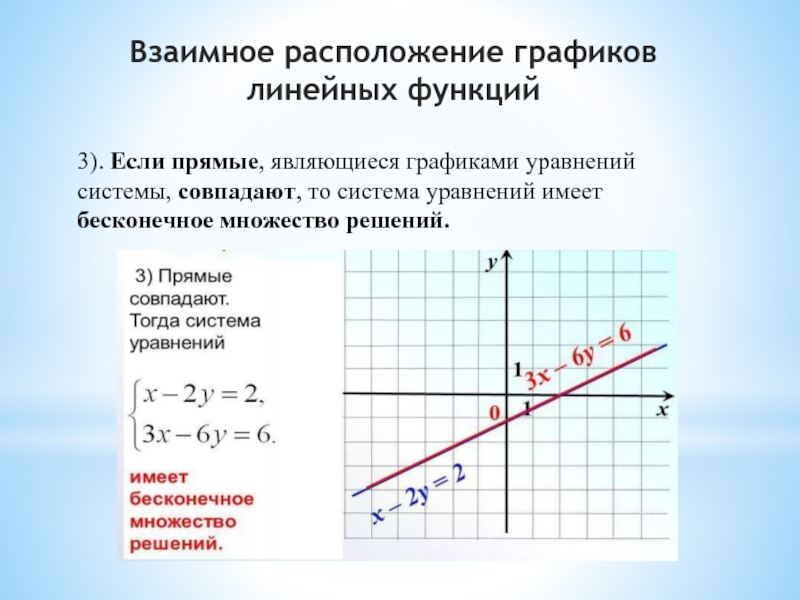
Слайд 93). Если прямые, являющиеся графиками уравнений системы, совпадают, то система уравнений
имеет бесконечное множество решений.
Взаимное расположение графиков линейных функций
Теги