Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Использование разнообразных форм современного урока �для обеспечения качества образования.
Содержание
- 1. Использование разнообразных форм современного урока �для обеспечения качества образования.
- 2. умение транслировать и формировать программный объем знанииумение
- 3. Современный урок –
- 4. Качество образования – это одна из основных проблем современной школы. Это процесс постоянного совершенствования.
- 5. Из чего оно складывается?из высокого уровня профессионализма
- 6. Целевые направления:совершенствование организации учебного процесса и повышение
- 7. Задачи:формирование установок на освоение современных педагогических технологий,
- 8. Составляющие качества образования:качество обученности школьников по образовательным
- 9. Педагогические качества: владение современными образовательными технологиями;способность делать
- 10. Технологии и методики применяемые на уроках математики:технология
- 11. Технология уровневой дифференциации.
- 12. Тема: «Объем прямоугольного параллелепипеда». Карточка №1Объём -это..История существования объёма.
- 13. Карточка №2Формулы - это..Единицы измерения пути, скорости, времени.Единица скорости – УЗЕЛ? Тема: «Формулы».
- 14. Тема: «Площадь». Карточка №3Измерения площадей на Руси.Единицы площадей: Гектар - это..Ар - это..
- 15. Карточка для слабого ученика. Покажи на рисунке:
- 16. Карточка для сильного ученика. Что такое круг?Хорда?Радиус?Диаметр?Как можно найти диаметр, не измеряя его?
- 17. ТЕСТОтвет «да» соответствует __, ответ «нет» -
- 18. КАРТОЧКА. «Сложение и вычитание
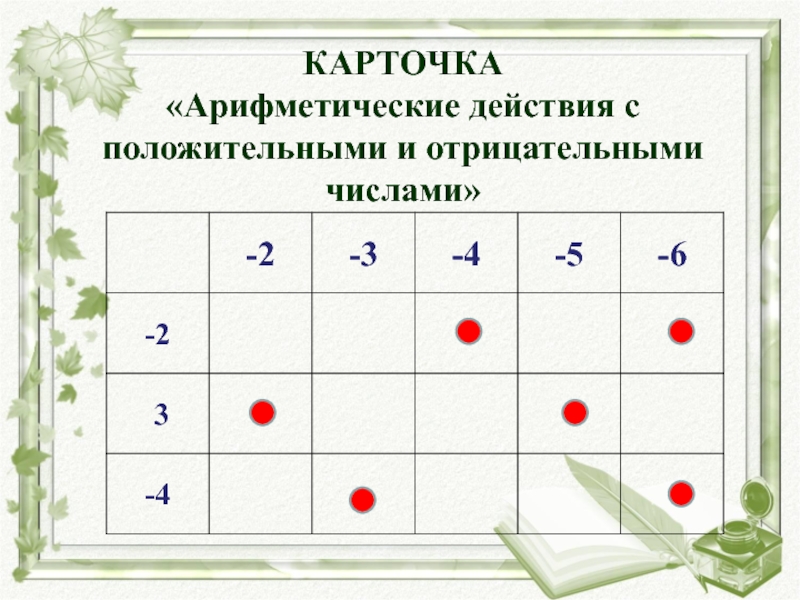
- 19. КАРТОЧКА «Арифметические действия с положительными и отрицательными числами»
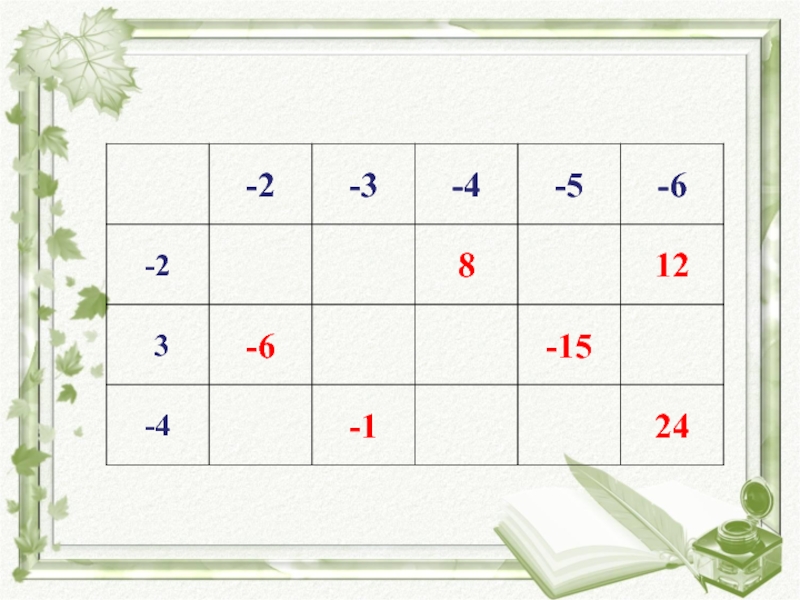
- 20. Слайд 20
- 21. Игра – творчество, игра – труд.
- 22. Игра «Диагонали» . Восстановите цепочку и
- 23. Игра «Разнеси почту»
- 24. Игра «Ярмарка-распродажа».В летнем лагере на каждого ученика
- 25. Технология проблемного обучения.
- 26. Равные части арбуза – называют ДОЛЯМИ.Так как
- 27. Равные части отрезка –ДОЛИ.Так как отрезок разделили
- 28. Тема: «Формула корней квадратного уравнения» Обезьянок
- 29. Далее по тексту задачи составляется уравнение. При
- 30. Это уравнение вида ax2 + bx + c = 0. Далее выясняется. Почему
- 31. Вынесение общего множителя x(ax+b)+c=0 по аналогии с решением
- 32. Если ученики высказывают сомнение можно ли решить
- 33. Рассмотрим рисунок. Решение представлено
- 34. Затем выясняется, что выражение y2 + y + 9 и 16
- 35. Далее учитель выделяет новую проблему: как изобразить
- 36. Если учащиеся, исходя из рисунка 2, предлагают
- 37. эта запись – алгебраическое тождество и в
- 38. Значит, если к выражению y2 – 6y прибавить 9, то получим
- 39. Требования проблемного обучения: Изучение темы начинается с
- 40. Внедрение ИКТ осуществляется по направлениям:создание презентаций к урокам;использование готовых обучающих программ; работа с ресурсами Интернет.
- 41. Слайд 41
- 42. Устный счёт. 57
- 43. Кости - кубики с обозначениями чисел от
- 44. В конце телевизионной программы «Время» всегда передают
- 45. Кости - кубики.Урок 1. 1. Используя знаки
- 46. 2. Бросили два белых кубика, выпало +3
- 47. Запишите сумму очков для каждого случая, изображенного
- 48. 3. На доске были записаны результаты нескольких
- 49. 4. а) (+)+(+)=…
- 50. Цель первого
- 51. Урок2: 5. Бросили
- 52. 6. Запишите сумму для каждого случая и
- 53. Слайд 53
- 54. 8. Сформулируйте выводы:Если выигрышных и проигрышных очков поровну, то получится …..
- 55. Цель второго
- 56. 9. Бросили три выигрышных
- 57. Цель третьего урока - установить опытным путем переместительность и сочетательность сложения.
- 58. Слайд 58
- 59. 11. Запишите по два примера на вычитание
- 60. Цель четвертого
- 61. Тема: «Логарифмические уравнения и неравенства».Цели
- 62. "Шаг вперёд!" Решить уравнения:
- 63. Актуализация знаний. Устные упражнения 1. Вычислить:
- 64. 2.Найти x, если 3.Сравнить с нулем:4. Упростить:
- 65. 5. Решить уравнения: 6. Решить неравенство:
- 66. Алгоритм работы: Начерти таблицу (лист
- 67. Затем каждый самостоятельно решает второе задание чужой
- 68. ЛИСТ УЧЕТА:
- 69. КАРТОЧКА №1Какова область определения логарифмической функции?Чему равна
- 70. КАРТОЧКА №2Чему равен логарифм произведения?Чему равен логарифм
- 71. КАРТОЧКА №3Назвать основные свойства логарифмической функции.Решить неравенство:
- 72. КАРТОЧКА №4Назвать основное логарифмическое тождество.Чему равна сумма
- 73. КАРТОЧКА №5Напишите формулу перехода от одного основания
- 74. КАРТОЧКА №6Какова область определения логарифмической функции?Назвать свойства
- 75. КОНТРОЛЬНАЯ РАБОТА Вариант 1. Решите
- 76. КОНТРОЛЬНАЯ РАБОТА Вариант 2. Решите
- 77. Для повышения качества образования необходимо:использовать на
- 78. Учителю нужно:более продуманно формулировать цели своей деятельности;ставить
- 79. Спасибо за внимание.
- 80. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ИСПОЛЬЗОВАНИЕ РАЗНООБРАЗНЫХ ФОРМ СОВРЕМЕННОГО УРОКА
ДЛЯ ОБЕСПЕЧЕНИЯ КАЧЕСТВА ОБРАЗОВАНИЯ.
А.А.Тажгалиева, учитель
математики МБОУ «Верхнебузанская СОШ»
Слайд 2
умение транслировать
и формировать программный
объем знании
умение решать творческие задачи,
формировать многомерное сознание,
развивать способности к самоактуализации.
Слайд 3 Современный урок – это урок,
в
результате которого открывается
и создается что-то новое, собственный продукт творчества:
открытие превращается в изобретение, изобретение - в проект, проект –
в технологии реальной действительности.
Слайд 4Качество образования – это одна из основных проблем современной школы.
Это процесс постоянного совершенствования.
Слайд 5Из чего оно складывается?
из высокого уровня профессионализма педагогов;
из создания комфортности
в обучении школьников;
прочности знаний учащихся;
из материально-технического обеспечения школы.
Слайд 6Целевые направления:
совершенствование организации учебного процесса и повышение результатов обучения;
создание условий
для повышения мотивации к обучению, саморазвитию, самостоятельности в принятии решений;
обеспечение
учебно-воспитательного процесса на современном уровне;создание условий для удовлетворения образовательных потребностей ребенка;
Слайд 7Задачи:
формирование установок на освоение современных педагогических технологий, подходов, обеспечивающих подготовку
качественно нового школьника;
создание единой системы урочной и внеурочной деятельности учителей
и учеников, направленной на разностороннее развитие образовательного процесса;Слайд 8Составляющие качества образования:
качество обученности школьников по образовательным областям;
качество сформированности общеучебных
умений школьников (умение работать с учебником, текстом, составить план, умение
анализировать, делать вывод и т.п.);качество развития личности школьников (эмоциональность, воля, познавательный интерес, мотивация и т. д.);
качество социальной адаптации (способность найти свою «нишу» в обществе).
Слайд 9Педагогические качества:
владение современными образовательными технологиями;
способность делать учебный материал доступным
пониманию;
творческое применение методов обучения;
способность организовать детский коллектив;
интерес
к детям;яркость речи, такт, связь с жизнью, способность к внеклассной работе.
Слайд 10Технологии и методики применяемые на уроках математики:
технология личностно-ориентированного образования;
технология уровневой
дифференциации;
технология игрового обучения;
технология системно - деятельностного подхода (проблемное обучение);
проектная деятельность;
здоровьесберегающие
технологии;информационно-коммуникационные технологии.
Слайд 12
Тема: «Объем прямоугольного параллелепипеда».
Карточка №1
Объём -это..
История существования объёма.
Слайд 13
Карточка №2
Формулы - это..
Единицы измерения пути, скорости, времени.
Единица скорости –
УЗЕЛ?
Тема: «Формулы».
Слайд 14
Тема: «Площадь».
Карточка №3
Измерения площадей на Руси.
Единицы площадей:
Гектар - это..
Ар
- это..
Слайд 15
Карточка для слабого ученика.
Покажи на рисунке: центр окружности, радиус, диаметр,
хорду.
Как можно найти диаметр,
не измеряя его?
Слайд 16
Карточка для сильного ученика.
Что такое круг?
Хорда?
Радиус?
Диаметр?
Как можно найти диаметр,
не измеряя его?
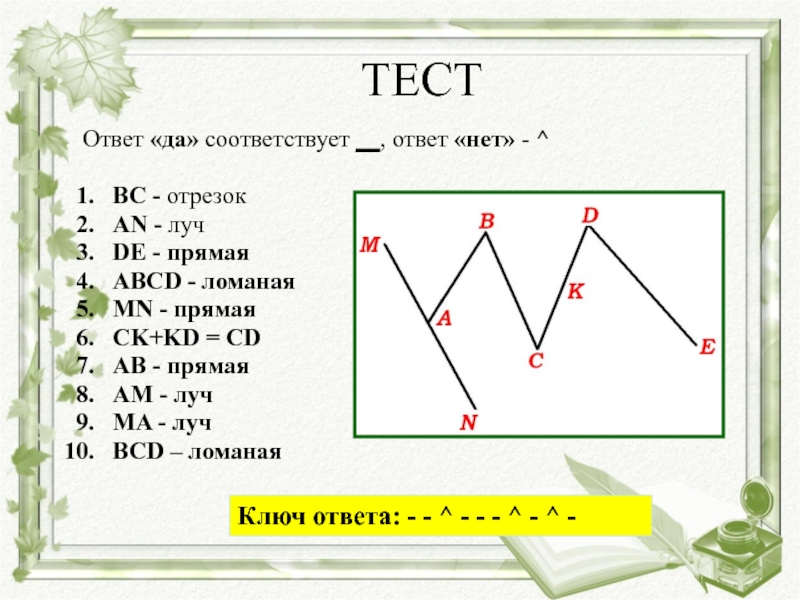
Слайд 17ТЕСТ
Ответ «да» соответствует __, ответ «нет» - ^
BC - отрезок
AN
- луч
DE - прямая
ABCD - ломаная
MN - прямая
CK+KD = CD
AB - прямая
AM - луч
MA - луч
BCD – ломаная
Ключ ответа: - - ^ - - - ^ - ^ -
Слайд 18
КАРТОЧКА.
«Сложение и вычитание десятичных дробей»
Вариант1
Вариант 2
27,3-(-2,6)= а 1. -5,6-3,7= а
-3,3-а+(-3,4)= в 2. 31,2-а+(-2,5)= в
-13-в-(-11,2)= с 3. -12-(-6,1)-в = с
(а+в)-с=g 4. (в+с)-а=g
КОДИРОВАННЫЕ ОТВЕТЫ:
1) -41,5; 2) -36,6; 3)-43,9; 4) 3,4; 5)-9,3; 6) 29,9;
7) 38; 8) 34,8.
Слайд 22
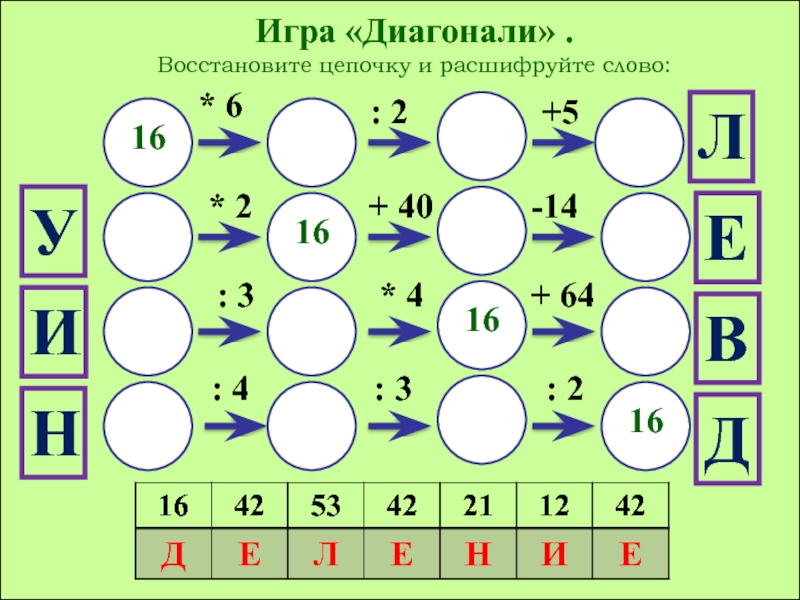
Игра «Диагонали» .
Восстановите цепочку и расшифруйте слово:
16
* 6
: 2
+5
Л
Е
В
Д
У
И
Н
* 2
+ 40 -14 : 3 * 4 + 64
: 4 : 3 : 2
16
16
16
Слайд 24Игра «Ярмарка-распродажа».
В летнем лагере на каждого ученика полагается 50г сахара
в день. В лагере 163 человека. Сколько килограмм пачек сахара
необходимо на неделю?Шоколад стоит 30р. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить за 190рублей в воскресенье?
Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?
Слайд 26Равные части арбуза – называют ДОЛЯМИ.
Так как арбуз разделили на
6 долей,
то одна доля «одна шестая арбуза»
Слайд 27Равные части отрезка –ДОЛИ.
Так как отрезок разделили на 7 долей,
то одна доля «одна седьмая отрезка»
Слайд 28
Тема: «Формула корней квадратного уравнения»
Обезьянок резвых стая
Всласть, поевши, развлекалась.
Их в
квадрате часть восьмая На поляне забавлялась. А двенадцать по лианам Стали прыгать, повисая… Сколько
ж было обезьянок, Ты скажи мне, в этой стае?
Слайд 29Далее по тексту задачи составляется уравнение. При этом учащиеся могут
допустить сами или учитель может спровоцировать следующую ошибку:
.
После проверки окончательно получаем уравнение:
Слайд 30Это уравнение вида ax2 + bx + c = 0. Далее выясняется. Почему оно называется квадратным,
являются ли квадратными уравнения вида ax2 + bx = 0, ax2 + c = 0, bx + c = 0.
Возникает проблема, как
решать такие уравнения? Затем рассматриваются предлагаемые учащимся пути решения неполных квадратных уравнений, предпринимаются безуспешные попытки решения полного уравнения, записанного в общем виде ax2 + bx + c = 0.
Слайд 31Вынесение общего множителя
x(ax+b)+c=0
по аналогии с решением уравнения
ax2 + bx = 0,
или перенос свободного члена
ax2 + bx = – c
по аналогии с уравнением
ax2 + c = 0
не
приносят желаемых результатов. Все попытки решения обсуждаются.
Слайд 32Если ученики высказывают сомнение можно ли решить эту задачу вообще,
учитель предъявляет им уравнение:
,которое ребята способны решить и в котором после проведённых преобразований «узнают» исходное уравнение. Один из вариантов решения предлагает учитель.
Слайд 33 Рассмотрим рисунок. Решение представлено на этом рисунке.
Это решение следует сопроводить записями: y +3=5, откуда y=2. y+3, как в
уравнении y+3= 5 появляется число 5; что сделано с обеими частями уравнения; где на рисунке добавленное к обеимчастям равенства число 9; является ли число – 8 корнем исходного уравнения; в ходе какой операции потерян этот корень; почему древние греки были обречены его потерять?
Слайд 34Затем выясняется, что выражение
y2 + y + 9 и 16 + 9
геометрически
представляют собой один и тот же квадрат, а исходное уравнение
и уравнение y2 + 6y – 16 + 9 – 9 = 0 – одно и то же уравнение, откуда и получаем, что y + 3 = ±5.Слайд 35Далее учитель выделяет новую проблему: как изобразить ситуацию геометрически, если
второй коэффициент в уравнении отрицателен?
Например, пусть уравнение имеет вид
y2 – 6y – 16 = 0. По аналогии с рассмотренной выше ситуацией, на рисунке появляются квадраты со сторонами y и y –3.
Слайд 36Если учащиеся, исходя из рисунка 2, предлагают рассмотреть равенство y2 = (y –
3)2 + 6(y – 3)+9, то после преобразований получим 0 = 0.
Слайд 37эта запись – алгебраическое тождество и в нём не использовано
условие, что
y2 – 6y – 16 = 0.
Преобразуя последнее равенство, получаем y2 –
6y = 16.На рисунке 2 находим «изображение» выражения y2 – 6y, и обращаем внимание, что в нём из площади квадрата со стороной y два раза вычитается площадь квадрата со стороной 3.
Слайд 38Значит, если к выражению y2 – 6y прибавить 9, то получим площадь квадрата со
стороной y – 3.
Заменяя выражение y2 – 6y равным ему числом 16, получим (y –3)2 =16+9,
т.е. y – 3 = ± = ± 5.Далее возникает очередная подпроблема: как представить рассмотренные решения квадратных уравнений в краткой алгебраической форме, обобщив геометрические решения. В результате такого обобщения получаем метод выделения полного квадрата.
Слайд 39Требования проблемного обучения:
Изучение темы начинается с ситуации невозможности решить практическую
задачу, обнаруженную в старинных рукописях.
Проблема разбивается на ряд подпроблем.
Решению проблемы
способствует рассмотрение истории решения квадратных уравнений.На уроке показаны два способа решения уравнения – геометрический и алгебраический.
В беседе рассмотрен ряд гипотез, не приведших к решению и ошибочные шаги.
Исторический материал естественно «вплетается» в содержание урока, делая его живым и занимательным.
Слайд 40Внедрение ИКТ осуществляется по направлениям:
создание презентаций к урокам;
использование готовых обучающих
программ;
работа с ресурсами Интернет.
Слайд 42Устный счёт.
57
64 28
93*36 *72 *95 *48
отметка «3» выставляется, если учащийся за 1 минуту высчитывает от 20 до 29 цифр;
отметка «4» — от 30 до 39 цифр;
отметка «5» — от 40 цифр.
Слайд 43Кости - кубики с обозначениями чисел от 1 до 6.
Весь материал разбит на 4 урока. Особое внимание следует уделить
записи действий.Слайд 44
В конце телевизионной программы «Время» всегда передают прогноз погоды на
завтра. Диктор может сказать: «Завтра в Москве 6 градусов
мороза, а в Астрахани 4 градуса тепла».МОСКВА …- 6 0С
АСТРАХАНЬ …+40С
Знак «+» означает тепло,
знак «–» означает холодно
Слайд 45Кости - кубики.
Урок 1. 1. Используя знаки «+» и «-»,
запишите число очков для каждого случая. Что обозначают знаки «+»
и «-»?
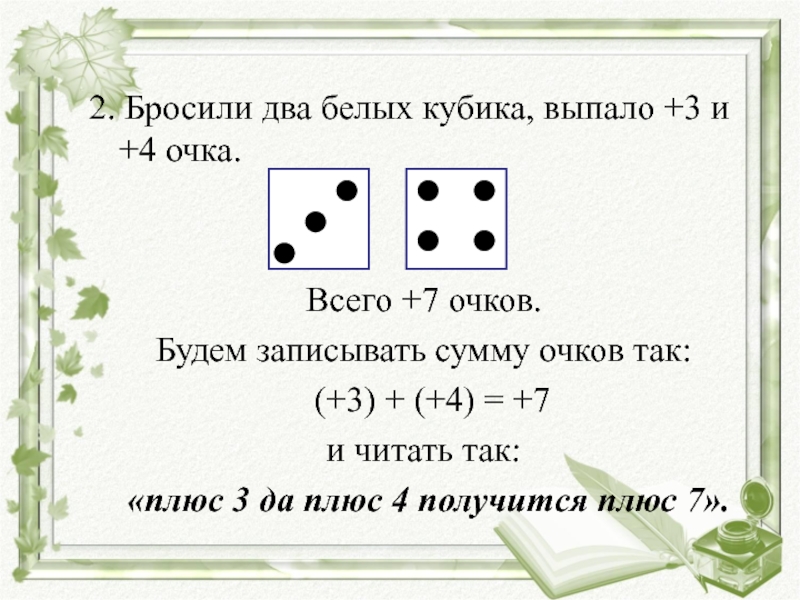
Слайд 462. Бросили два белых кубика, выпало +3 и +4 очка.
Всего +7 очков.
Будем записывать сумму очков так:
(+3)
+ (+4) = +7 и читать так:
«плюс 3 да плюс 4 получится плюс 7».
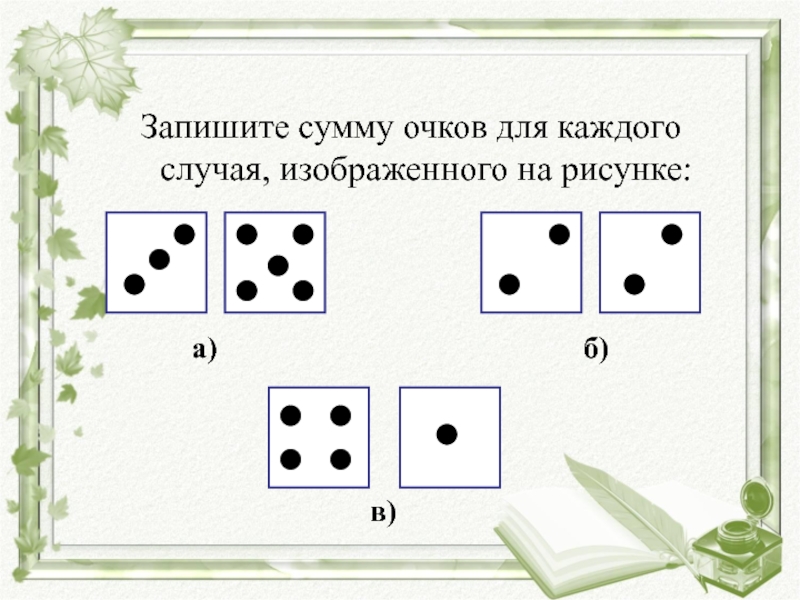
Слайд 483. На доске были записаны результаты нескольких опытов. На перемене
учитель стер часть записей. Восстановите записи:
а) (+5)+(+6)= в) (+4)+( )= +5б) (-5)+(-3)= г) (-3)+( )=+-5
д) ( )+(+2)= +3
е) ( )+(-6)= -11
Слайд 494. а) (+)+(+)=…
б) (-)+(-)= …
Выигрыш да выигрыш – получится …..
Проигрыш да проигрыш
– получится…..Слайд 50 Цель первого урока – создать
устойчивую ассоциативную связь:
белый цвет – выигрыш,
черный цвет –
проигрыш, а также научить детей находить сумму очков для кубиков одного цвета.
Слайд 51 Урок2: 5. Бросили два кубика разных
цветов. Выпало +3 и -5 очков.
Очевидно, что сумма очков равна -2, так как проигрышных очков на 2 больше, чем выигрышных. Сумму очков будем записывать так: (+3)+(--5)=-2 и читать так:«плюс 3 да минус 5 получится минус 2»
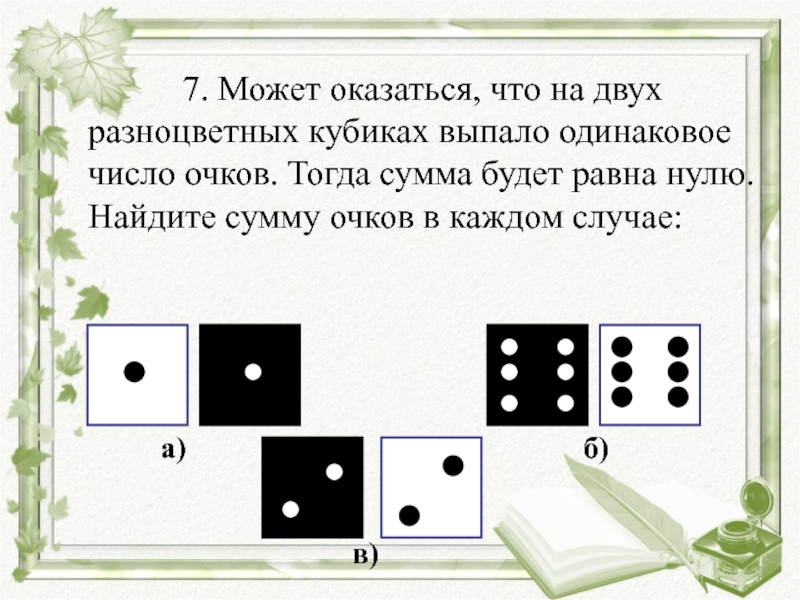
Слайд 53 7. Может оказаться,
что на двух разноцветных кубиках выпало одинаковое число очков. Тогда
сумма будет равна нулю. Найдите сумму очков в каждом случае: а) б)
в)
Слайд 55 Цель второго урока –
научить
находить сумму очков для кубиков разного цвета; заданием на восстановление
записи готовить к пониманию вычитанияСлайд 56 9. Бросили три выигрышных кубика. К сумме
очков первых кубиков прибавили число очков третьего кубика. Потом к
числу очков первого кубика прибавили сумму очков второго и третьего кубиков. Получатся ли одинаковые результаты? Выполняется ли это свойство для трех кубиков черного цвета? А для трех кубиков разного цвета?Слайд 57 Цель третьего урока - установить
опытным путем переместительность и сочетательность сложения.
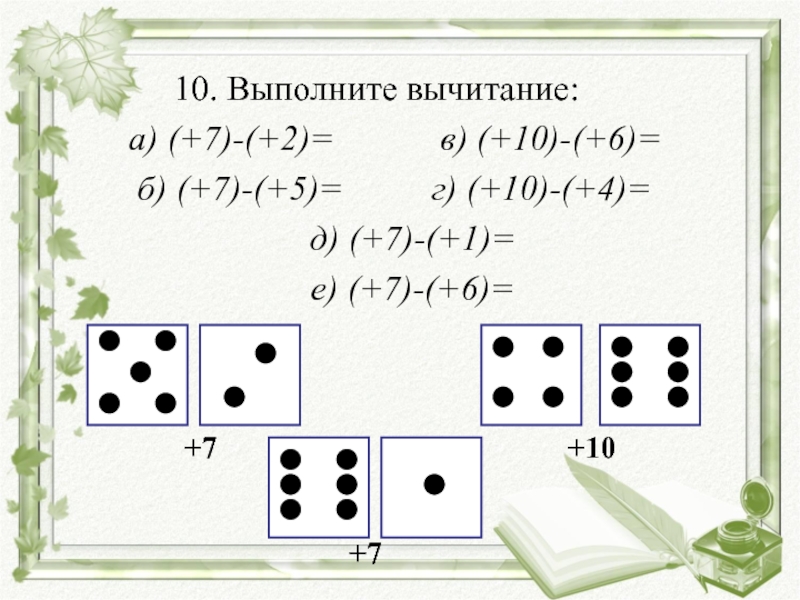
Слайд 58
10. Выполните вычитание:
а) (+7)-(+2)=
в) (+10)-(+6)=б) (+7)-(+5)= г) (+10)-(+4)=
д) (+7)-(+1)=
е) (+7)-(+6)=
+7 +10
+7
Слайд 5911. Запишите по два примера на вычитание сумму для каждого
случая. Найдите разность, сделайте проверку сложением:
-7
-7 +2 -3
Слайд 60 Цель четвертого урока - обучить
вычитанию и переходу от вычитания к сложению, а также подготовить
к изучению умножения и деления.Слайд 61Тема:
«Логарифмические уравнения
и неравенства».
Цели урока: самостоятельно изучить тему урока,
используя коллективные способы обучения (методику "Взаимообмен заданиями").
Задачи дня: вычислите log45log56log67log78.
Слайд 655. Решить уравнения:
6. Решить неравенство:
< 0
7. Найти область определения
функции:8. Упростить, используя свойство логарифма степени:
Слайд 66
Алгоритм работы:
Начерти таблицу (лист учета, в котором 6 заданий).
Отметить «+» номер карточки, которую решаешь.
Получив карточку, проработай ее вместе
с соседом: ответьте на вопросы карточки и решите ее вместе (то есть на первом этапе работают соседи по парте)Проверь свои ответы у учителя.
Если решение верное, то сделай отметку в листе учета и ищи нового партнера (не забудь взять такую же карточку у учителя, чтобы с ней работать с новым партнером).
Встретившись с новым партнером, объясни ему первое задание из своей карточки, затем твой товарищ объяснит первое задание своей карточки, может записать тебе в тетрадь это задание.
Слайд 67Затем каждый самостоятельно решает второе задание чужой карточки, сверяется решениями,
делает отметку в листе учета, и пара распадается - каждый
ищет нового партнера, работать он может теперь или со своей прежней карточкой , или с новой карточкой.Сверяетесь друг с другом с ответами вторых заданий : если задания решены верны, то ищите новых партнеров, а если есть расхождения, то помогаете товарищу найти ошибку, исправит ее.
Если у тебя появилось свободное время, то можешь решать «ЗАДАЧУ ДНЯ» или попытайся решать задания из рубрики «ШАГ В ПЕРЕД!»
Если ты успешно проработал все 6 карточек, то приступай к выполнению к/р, которую надо решить дома. Эта первая к/р, т.к. работа по этой теме на более высоком уровне продолжится на последующих уроках, после изучения темы будет новая к/р.
Слайд 69
КАРТОЧКА №1
Какова область определения логарифмической функции?
Чему равна сумма и разность
логарифмов с одним основанием?
Решите уравнения:
loga (x2 - 4x - 5)
= loga(7 - 3x).log4 (3x – 4) – log4(5 - x2).
Слайд 70
КАРТОЧКА №2
Чему равен логарифм произведения?
Чему равен логарифм степени?
Чему равен логарифм
частного?
Решите уравнения:
loga x = 2 loga 3 + loga 5.
logа
x – logа 10 = loga 2.Слайд 71
КАРТОЧКА №3
Назвать основные свойства логарифмической функции.
Решить неравенство: logа x >
loga c (рассмотреть 2 случая: 1) 0
a>1).Решите неравенства:
log3 x + log3(x - 1) – 1 < log32
log0,5 (x2 - 4x + 3) < 1
Слайд 72
КАРТОЧКА №4
Назвать основное логарифмическое тождество.
Чему равна сумма логарифмов с одним
основанием?
Решите систему уравнений:
log3 x + log3
y = 1. x + y = 7y - 3x = 8. lgx + lgy = 1
1) 2)
Слайд 73
КАРТОЧКА №5
Напишите формулу перехода от одного основания к другому.
Чему равен
loga а, loga 1?
Чему равен логарифм произведения положительных чисел?
Решите уравнения:
log0,25
(x2 – 5) = 1– log0,25(4x).log1,2 x2 = log1,2(4х - 3).
Слайд 74
КАРТОЧКА №6
Какова область определения логарифмической функции?
Назвать свойства возрастающей и убывающей
логарифмической функции.
Решите неравенства:
log2x2 + 2lgx > 1.
log24x + log4 (4x)
– 3 > 1,5Слайд 75
КОНТРОЛЬНАЯ РАБОТА
Вариант 1.
Решите уравнения:
2lg2x – lgx – 2 =
0;
log2x + 3 = 0,5log2 9;
log2x + log8x = 8;
log2
log3x = 2.Решите неравенства:
log5 (2x + 1) > log5(x – 1);
2.
3.
Слайд 76
КОНТРОЛЬНАЯ РАБОТА
Вариант 2.
Решите уравнения:
3log22x–2log2x–1= 0;
lg(x+2)=lg5–lg(x – 2);
log3x +
log9x = 6;
log3 log9x = 1.
Решите неравенства:
1.
2.
3.
Слайд 77Для повышения качества образования необходимо:
использовать на уроках
и во внеурочное время современные инновационные методики,
новые формы организации и проведения учебных занятий;активнее и шире использовать на уроках современные педагогические технологии, возможности информационно-коммуникационных технологий, сети Интернет.
Слайд 78Учителю нужно:
более продуманно формулировать цели своей деятельности;
ставить конкретные задачи;
прослеживать траекторию
развития своей собственной педагогической деятельности;
отслеживать уровень мотивации учащихся;
наметить шаги по
его повышению с помощью разнообразных форм внеклассной работы;отследить наиболее успешные направления внеклассной работы, которые вызывают интерес у большинства учащихся.