Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
На острове Дробей. Презентация к уроку. 6 класс
Содержание
- 1. На острове Дробей. Презентация к уроку. 6 класс
- 2. Французский писатель XIX столетия Анатоль Франс“Учиться
- 3. Без дробей невозможна наша жизнь!ГИПОТЕЗА:
- 4. Как повлияло на развитие человечества открытие ДРОБЕЙ ?ПРОБЛЕМА:
- 5. Цели и задачиРебята, сегодня мы с вами
- 6. Изисториидробей
- 7. Одним из самых сложных разделов математики по
- 8. Слайд 8
- 9. Что такое дробь? Когда возникла необходимость делить
- 10. Слайд 10
- 11. Слайд 11
- 12. С годами усложнялись операции, проделываемые с дробями,
- 13. ВыводСам термин «дробь» имеет арабские корни и
- 14. «Немного теории..» Цель: Сформулировать правила сравнения,
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Дроби на РусиНа русской земле первым математиком,
- 20. -Половина, полтина-Треть-Четь-Пятина-Полтреть-Седьмина-Полчеть- Десятина-Пол-полтретьПол-пол-треть (малая)-Пол-полчеть-Пол-полчеть (Малая) В русском языке
- 21. ВЫВОД: Человек научился классифицировать дроби наблюдая за природой!
- 22. Показать применение дробей; Предложить примеры, задачи для решенияПРАКТИКИ:
- 23. Лабиринт – первое препятствие на нашем пути, которое
- 24. 2. Исключите целую часть из числа
- 25. 3. Переведите число в неправильную дробь
- 26. Лабиринт мы одолели,Все препятствия прошли!И до лестницы
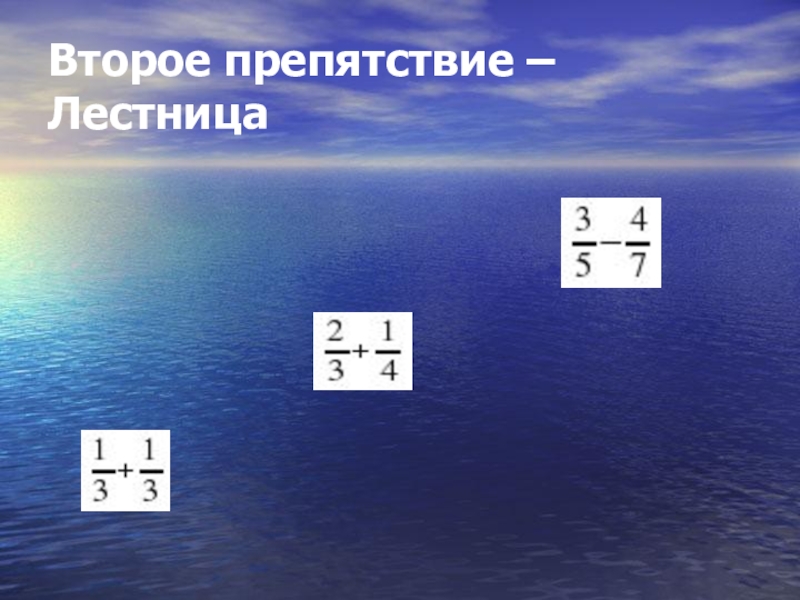
- 27. Второе препятствие – Лестница
- 28. Мы и лестницу прошли.В коридор все мы вошли.Здесь вопросы ждут ответ.Их осилим или нет?
- 29. Практическая работа. (работа в паре)
- 30. Остановка «Горы Мозгодром». Выполните действия
- 31. Задача 1Вычислите, какова ширина острова Дробей, если
- 32. Задача 2Вычислите температуру воды в минеральном источнике, если она составляет температуры кипения
- 33. Остановка «Замок Тестирование».(проверь себя!)1.Представтьте дробь в виде
- 34. Ответы: 1 – а2 –а3 -б4 - а
- 35. Вывод Систематизация начальных знаний о дробях помогла нам проще усвоить тему.
- 36. ФИЗКУЛЬТМИНУТКАВыше – выше потянулись.Ну-ка, плечи распрямите,Поднимите, опустите.Вправо,
- 37. Слайд 37
- 38. Результаты анкетирования
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. Слайд 43
- 44. Что понравилось больше всего?Чему новому ты научился?Закончи
- 45. Вывод:Многообразен мир дробей.Они в нашей жизни везде!Мы их встречаем везде!Они в примерах, в задачах.
- 46. «Сколько было участников экспедиции»? Если считать их
- 47. Скачать презентанцию
Французский писатель XIX столетия Анатоль Франс“Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.
Слайды и текст этой презентации
Слайд 2Французский писатель
XIX столетия Анатоль Франс
“Учиться можно только весело…
Чтобы
переваривать знания,
надо поглощать их
с аппетитом”.
Слайд 5Цели и задачи
Ребята, сегодня мы с вами отправляемся в необычное
путешествие, мы посетим остров Дробей. В этой стране мы сделаем
несколько остановок: в деревне Теоретической, побродим в лесу Историческом, отдохнём на поляне Дробная, попробуем одолеть горы Мозгодром, посетим замок Тестирование. На каждой остановке вам надо показать свои знания, внимательность и находчивость.Слайд 7
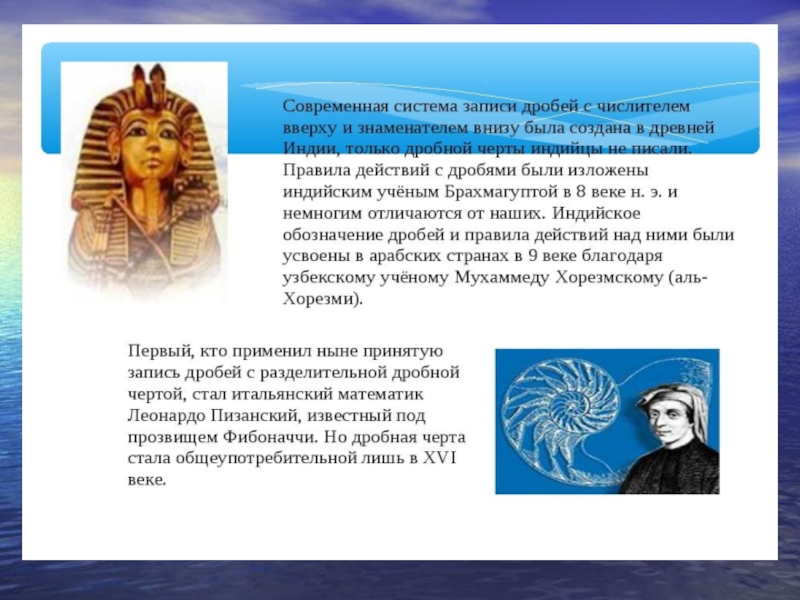
Одним из самых сложных разделов математики по сей день считаются
дроби. История дробей насчитывает не одно тысячелетие. Умение делить целое
на части возникло на территории древнего Египта и Вавилона.Слайд 9
Что такое дробь? Когда возникла необходимость делить целое на части
без лишних усилий, тогда и появились дроби.
Слайд 12С годами усложнялись операции, проделываемые с дробями, менялась форма их
записи. У каждого государства древнего мира были свои особенности во
«взаимоотношениях» с этим разделом математики.Слайд 13Вывод
Сам термин «дробь» имеет арабские корни и происходит от слова,
обозначающего «ломать, разделять». С древних времен в этом смысле мало
что изменилось. Современное определение звучит следующим образом: дробь — это часть или сумма частей единицы. Соответственно, примеры с дробями представляют собой последовательное выполнение математических операций с долями чисел.Слайд 14«Немного теории..» Цель: Сформулировать правила сравнения, сложения и вычитания обыкновенных дробей с
разными знаменателями и научиться их применять.
Сформулировать правила сравнения, сложения и
вычитания обыкновенных дробей с разными знаменателями и научиться их применять.
«Немного теории..»
Цель:
Слайд 19Дроби на Руси
На русской земле первым математиком, изложившим деление целого
на части, стал новгородский монах Кирик. В 1136 году он
написал труд, в котором изложил метод «счисления лет». Кирик занимался вопросами хронологии и календаряДеление целого на части применялось при расчете размера налога в XV-XVII веках. Использовались операции сложения, вычитания, деления и умножения с дробными частями.
Само слово «дробь» появилось на Руси в VIII веке. Оно произошло от глагола «дробить, разделять на части». Для названия дробей наши предки использовали специальные слова. Например, 1/2 обозначалась как половина или полтина, 1/4 — четь, 1/8 — полчеть, 1/16 — полполчеть и так далее.
Слайд 20-Половина, полтина
-Треть
-Четь
-Пятина
-Полтреть
-Седьмина
-Полчеть
- Десятина
-Пол-полтреть
Пол-пол-треть (малая)
-Пол-полчеть
-Пол-полчеть (Малая)
В русском языке слово "дробь" появилось
лишь в VIII веке. Происходит слово "дробь" от слова "дробить,
разбивать, ломать на части". У других народов название дроби также связано с глаголами "ломать", "разбивать", "раздроблять". В первых учебниках дроби назывались"ломанные числа". В старых руководствах находили следующие названия дробей на Руси:Слайд 23Лабиринт – первое препятствие на нашем пути, которое состоит их трёх
дверей. Откроются они, если мы решим следующие задания:
1. Сократите дроби
Слайд 26Лабиринт мы одолели,
Все препятствия прошли!
И до лестницы дошли!
А она ведь
не простая,
И ничуть не золотая.
Там примерчики живут.
И решений своих ждут.
Слайд 29Практическая работа.
(работа в паре)
I вариант
II вариант
Закрасьте ¼ часть круга Закрасьте 2/8 части круга
Сравните, сделайте вывод. Какие получились дроби?
Закрасьте 2/6 части прямоугольника Закрасьте 1/3 часть прямоугольника
Сравните, сделайте вывод, запишите математически. Какие получились дроби?
Слайд 31Задача 1
Вычислите, какова ширина острова Дробей, если длины
острова на
2 км больше её половины
Слайд 32Задача 2
Вычислите температуру воды в минеральном источнике, если она составляет
температуры кипения
Слайд 33Остановка «Замок Тестирование».(проверь себя!)
1.Представтьте дробь в виде десятичной дроби.
а) 0,25;
б)0,025; в) 0,52; г)
0,052.2.Вычислите: + .
а)1,15; б) 1,25; в) 1 ; г) 2,15.
3. В корзине 0,6 всех имеющихся фруктов – яблоки. Выразите эту долю в процентах.
а) 6%; б)60%; в)0,6%; г) %.
4.Найдите числа 45.
а) 20; б)25; в) 9; г)
Слайд 36ФИЗКУЛЬТМИНУТКА
Выше – выше потянулись.
Ну-ка, плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями
коснитесь.
Сели, встали. Сели, встали.
И на месте побежали.
Слайд 43
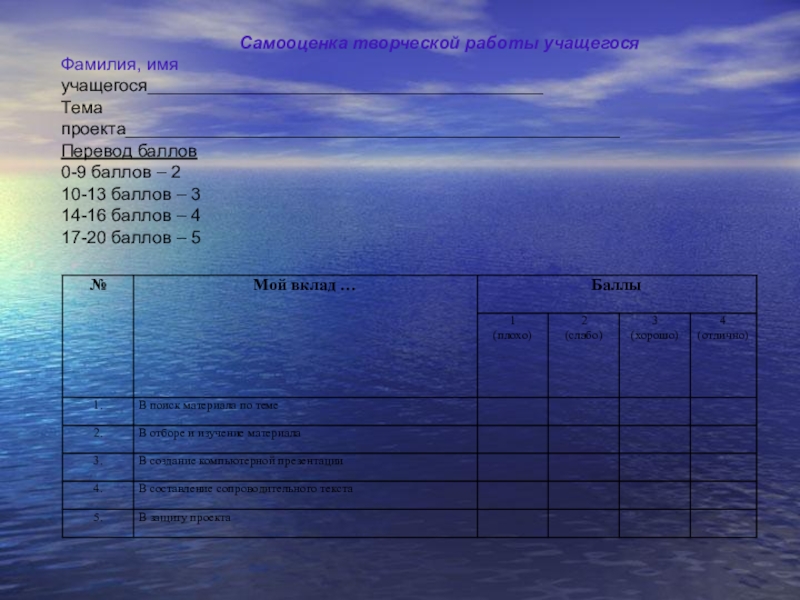
Самооценка творческой
работы учащегосяФамилия, имя учащегося________________________________________
Тема проекта__________________________________________________
Перевод баллов
0-9 баллов – 2
10-13 баллов – 3
14-16 баллов – 4
17-20 баллов – 5
Слайд 44Что понравилось больше всего?
Чему новому ты научился?
Закончи предложение
- Своей работой
над проектом я доволен (не доволен), так как…
Слайд 45
Вывод:
Многообразен мир дробей.
Они в нашей жизни везде!
Мы их встречаем везде!
Они
в примерах, в задачах.
Слайд 46«Сколько было участников экспедиции»? Если считать их парами, то 1
человек останется, а если считать их по три или по
пять человек, то все равно 1 человек останется. Еще известно, что их больше 50, но меньше 80.Домашняя задача