Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллелограмм 8 класс
Содержание
- 1. Параллелограмм 8 класс
- 2. ПараллелограммЦель:1. Ввести понятие параллелограмма.2. Рассмотреть свойства параллелограмма.3.
- 3. Ответьте на вопросыСформулировать признаки равенства треугольников.Какие углы
- 4. Обозначение параллелограмма: АВСD: AB||CD,
- 5. Рис. 1. Дано:
- 6. Свойства параллелограмма Рассмотрите стороны, углы и
- 7. Свойства параллелограмма Что дано по условию
- 8. Докажите самостоятельноСвойства параллелограмма Теорема. В параллелограмме сумма углов, прилежащих к одной стороне равна 180°
- 9. Решить задачи №376б, 372б, 371б№376бКак расположены
- 10. Домашнее заданиеП.42, вопросы 6-8 на стр.114 Решить задачи № 371а, 372в, 376в,г
- 11. Скачать презентанцию
ПараллелограммЦель:1. Ввести понятие параллелограмма.2. Рассмотреть свойства параллелограмма.3. Научиться применять свойства параллелограмма для решения задач.Учитель математики МБОУ-СОШ №7 г. Клинцы Коваленко С.Ф.
Слайды и текст этой презентации
Слайд 1Урок математики в 8 классе по теме «Параллелограмм»
Учитель математики МБОУ-СОШ
№7 г. Клинцы
Коваленко С.Ф.
Слайд 2Параллелограмм
Цель:
1. Ввести понятие параллелограмма.
2. Рассмотреть свойства параллелограмма.
3. Научиться применять свойства
параллелограмма для решения задач.
Учитель математики МБОУ-СОШ №7 г. Клинцы
Коваленко С.Ф.
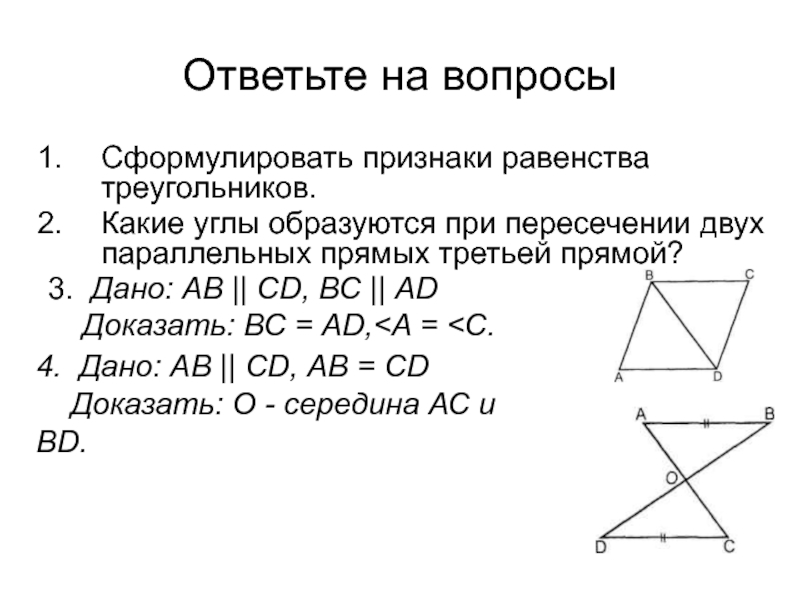
Слайд 3Ответьте на вопросы
Сформулировать признаки равенства треугольников.
Какие углы образуются при пересечении
двух параллельных прямых третьей прямой?
3. Дано: АВ || CD, ВС
|| ADДоказать: ВС = AD,
4. Дано: АВ || CD, АВ = CD
Доказать: О - середина АС и BD.
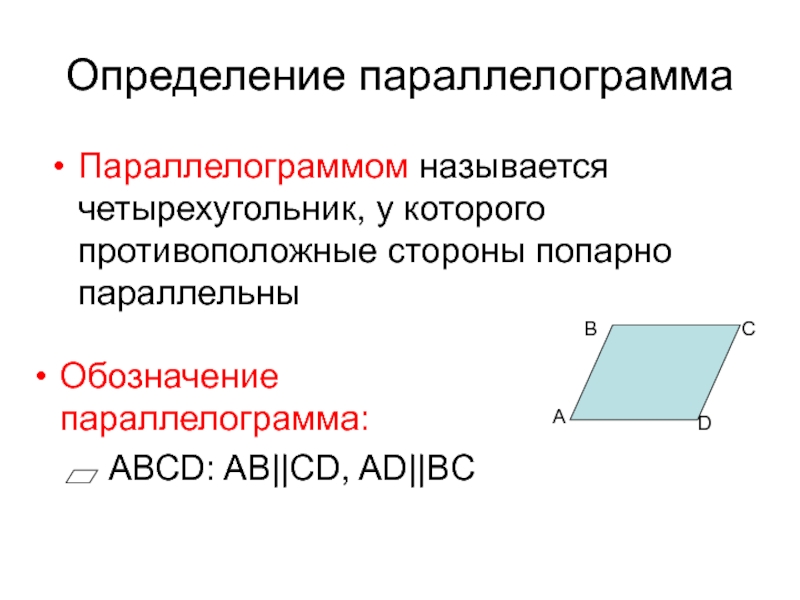
Слайд 4Обозначение параллелограмма:
АВСD: AB||CD, AD||BC
Определение параллелограмма
Параллелограммом называется
четырехугольник, у которого противоположные стороны попарно параллельны
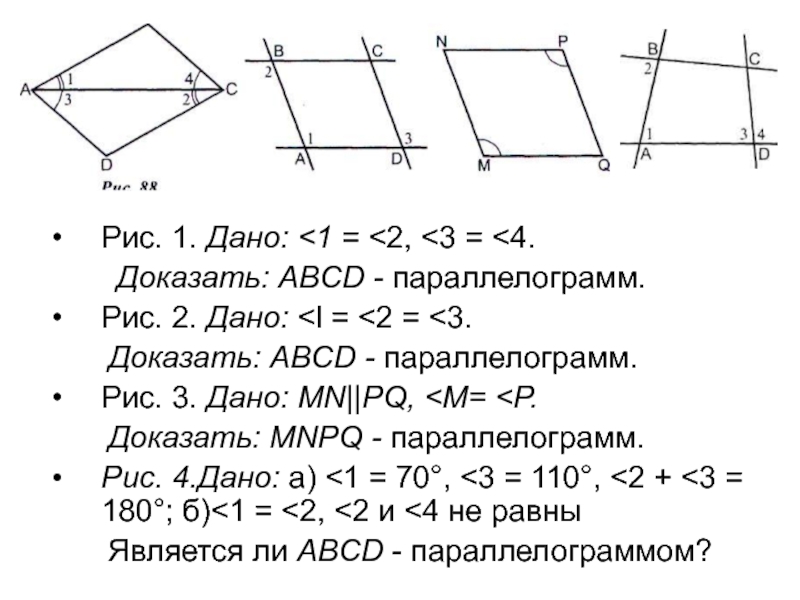
Слайд 5Рис. 1. Дано:
Доказать: ABCD - параллелограмм.
Рис. 2. Дано:
= <2 = <3.Доказать: ABCD - параллелограмм.
Рис. 3. Дано: MN||PQ,
Рис. 4.Дано: a) <1 = 70°, <3 = 110°, <2 + <3 = 180°; б)<1 = <2, <2 и <4 не равны
Является ли ABCD - параллелограммом?
Слайд 6Свойства параллелограмма Рассмотрите стороны, углы и диагонали параллелограмма и сформулируйте
его свойства.
Что дано по условию теоремы?
Дано: ABCD- параллелограмм.
Что надо
доказать?Доказать: АВ=СD, AD=BC,
Что помогает доказывать равенство отрезков, равенство углов?
Как их получить?
1. Проведем диагональ АС. Какие фигуры появились? Что о них можно сказать?
2. Треугольники ВАС = DCA, т.к.
АС - общая сторона
<1=<2 <3=<4 (как накрест лежащие при параллельных прямых)
4. Т.к. треугольники ВАС и DCA равны,
то соответствующие стороны АВ=СD, AD=BC
и соответствующие углы
Теорема.
В параллелограмме противоположные стороны и противоположные углы равны.
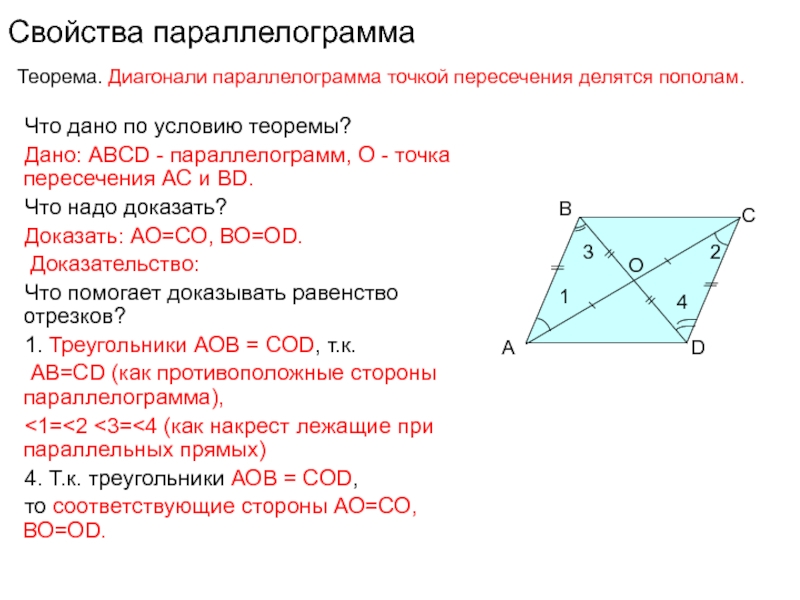
Слайд 7Свойства параллелограмма
Что дано по условию теоремы?
Дано: ABCD - параллелограмм,
О - точка пересечения АС и ВD.
Что надо доказать?
Доказать:
АО=СО, ВО=ОD.Доказательство:
Что помогает доказывать равенство отрезков?
1. Треугольники АОВ = CОD, т.к.
АВ=СD (как противоположные стороны параллелограмма),
<1=<2 <3=<4 (как накрест лежащие при параллельных прямых)
4. Т.к. треугольники АОВ = CОD,
то соответствующие стороны АО=СО, ВО=ОD.
Теорема. Диагонали параллелограмма точкой пересечения делятся пополам.
Слайд 8Докажите самостоятельно
Свойства параллелограмма
Теорема. В параллелограмме сумма углов, прилежащих к
одной стороне равна 180°
Слайд 9Решить задачи
№376б, 372б, 371б
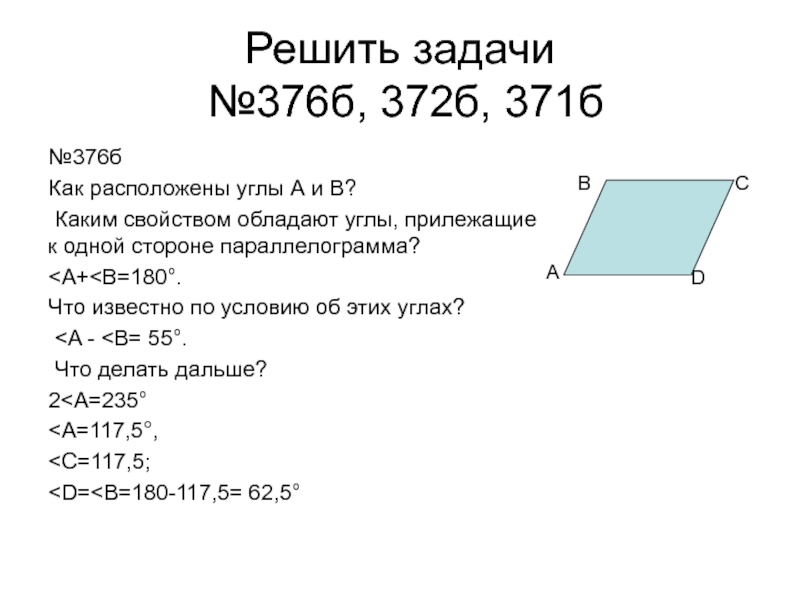
№376б
Как расположены углы А и В?
Каким свойством обладают углы, прилежащие к одной стороне параллелограмма?
Что известно по условию об этих углах?
Что делать дальше?
2