Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Площади многоугольников на клетчатой бумаге 5 класс
Содержание
- 1. Площади многоугольников на клетчатой бумаге 5 класс
- 2. Геометрия является самым могущественным средством для изощрения
- 3. Проблема: Существует ли универсальный способ нахождения площади
- 4. Объект исследования: фигуры на клетчатой бумаге.Предмет исследования:
- 5. Способы нахождения площадей многоугольников, изображенных на клетчатой
- 6. Нахождение площади фигуры, используя формулы геометрииЗадача
- 7. Нахождение площади фигуры, используя формулы геометрии
- 8. Площадь многоугольника как сумма площадей её
- 9. Площадь фигуры как часть площади прямоугольникаЗадача .
- 10. Площадь фигуры как часть площади прямоугольника
- 11. Георг Алекса́ндр Пик ( 10 августа
- 12. Формула Пика S = В + Г :
- 13. Задача. Найдите площадь пятиугольника, изображенного на клетчатой
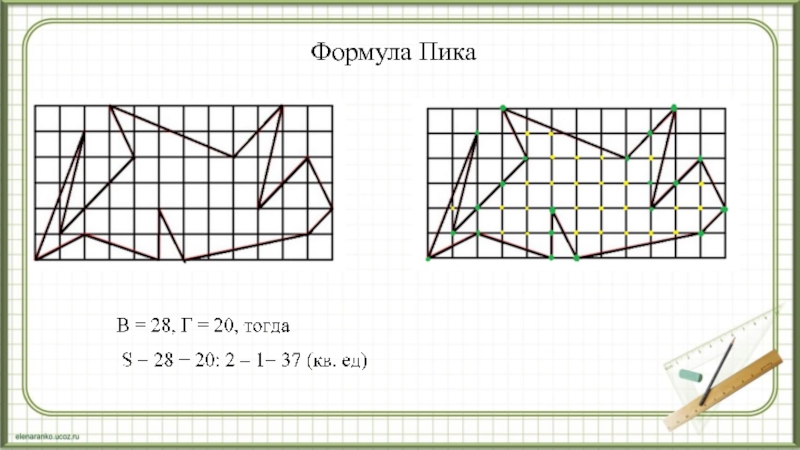
- 14. Формула Пика
- 15. ГипотезаСамый эффективный способ нахождения площадей на клетчатой бумаге – решение задач по формуле Пика.
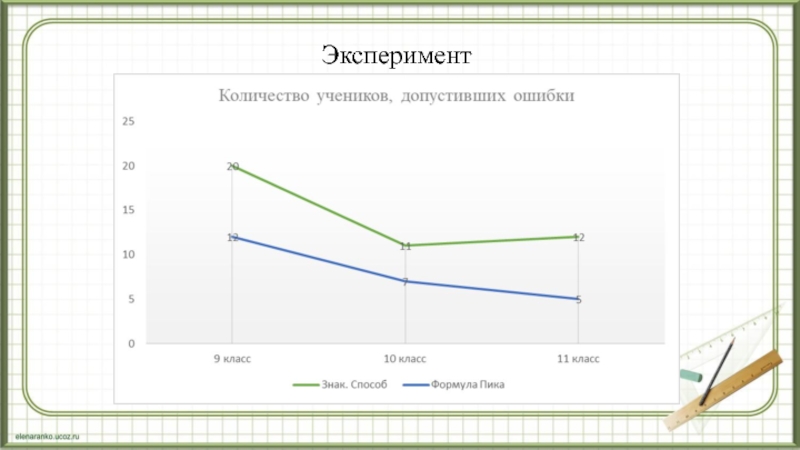
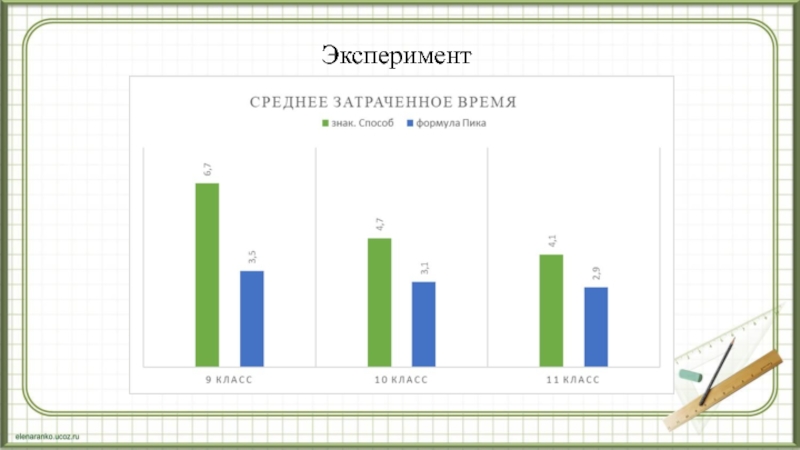
- 16. Эксперимент
- 17. Слайд 17
- 18. ЗаключениеПроведенный эксперимент показал, что: 1) ранее семь
- 19. Эксперимент
- 20. Эксперимент
- 21. Выводы: В результате работы над данной темой
- 22. Список литературы и источников 1. Википедия.
- 23. Спасибо за внимание!
- 24. Скачать презентанцию
Геометрия является самым могущественным средством для изощрения наших умственных способностей и даёт нам возможность правильно мыслить и рассуждать. /Г. Галилей/
Слайды и текст этой презентации
Слайд 2Геометрия является самым могущественным средством
для изощрения наших умственных способностей
и даёт нам возможность
Галилей/Слайд 3Проблема: Существует ли универсальный способ нахождения площади произвольного многоугольника, изображенного
на клетчатой бумаге?
Цель работы:
1. Изучить способы нахождения площадей на
клетчатой бумаге.2. Найти самый эффективный способ решения задач.
Задачи:
1. Изучить литературу по данной теме.
2. Рассмотреть разные способы нахождения площадей фигур на клетчатой бумаге.
3. Провести эксперимент.
4. Сделать выводы.
.
Слайд 4Объект исследования: фигуры на клетчатой бумаге.
Предмет исследования: площадь фигур.
Методы исследования:
1) теоретический: изучение литературы и других источников информации;
2) эмпирический: тестирование, анкетирование;3) математический: вычисления,
построение диаграмм.
Слайд 5Способы нахождения площадей многоугольников,
изображенных на клетчатой бумаге
1. Площадь многоугольника можно
находить, разбивая его на квадраты, прямоугольники, треугольники.
2. Многоугольник путем
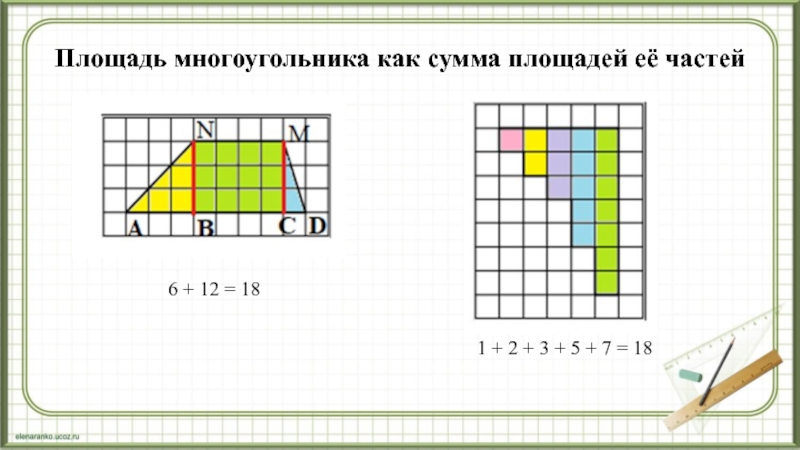
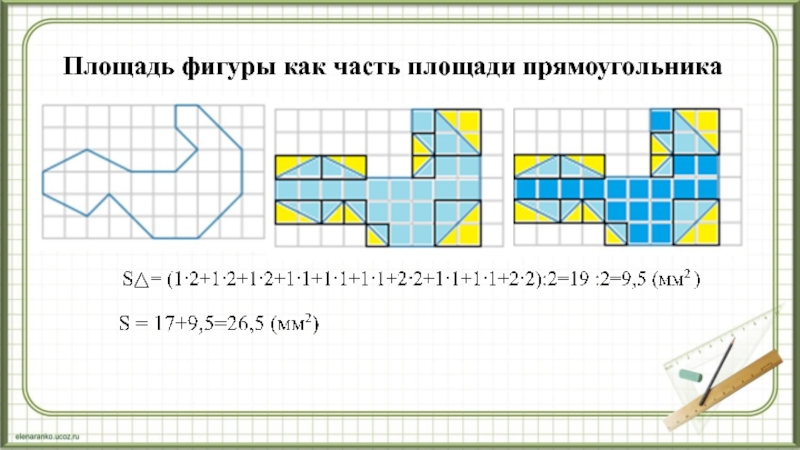
разрезания и перекладывания можно преобразовать в другой многоугольник с такой же площадью. 3. Площадь целого многоугольника равна сумме площадей его частей.
4. Формула Пика.
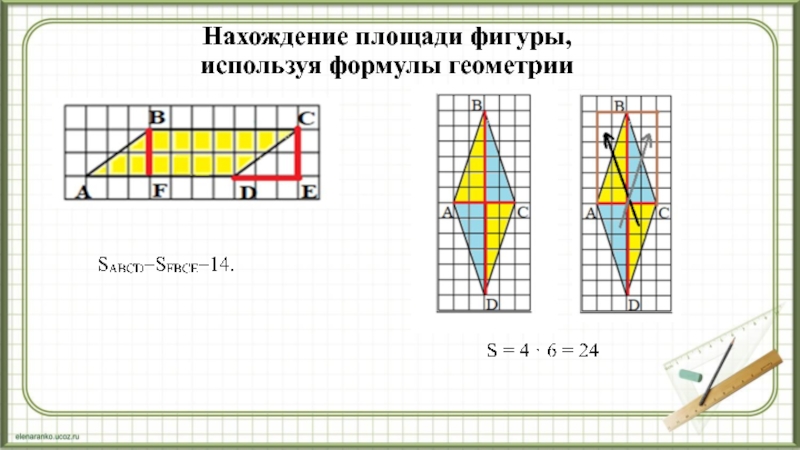
Слайд 6Нахождение площади фигуры,
используя формулы геометрии
Задача . На клетчатой бумаге
с размером клетки 1×1 изображён треугольник ABC. Найдите его площадь.
Каждый
прямоугольный треугольник можно дополнить до прямоугольника, площадь большего прямоугольника состоит из 9 клеток, а меньшего из 3 клеток, площадь целого прямоугольника равна 12 (9 + 3 = 12). Мы знаем, что площадь прямоугольного треугольника в 2 раза меньше площади прямоугольника, следовательно, площадь треугольника равна 6 (12: 2 = 6). Слайд 9Площадь фигуры как часть площади прямоугольника
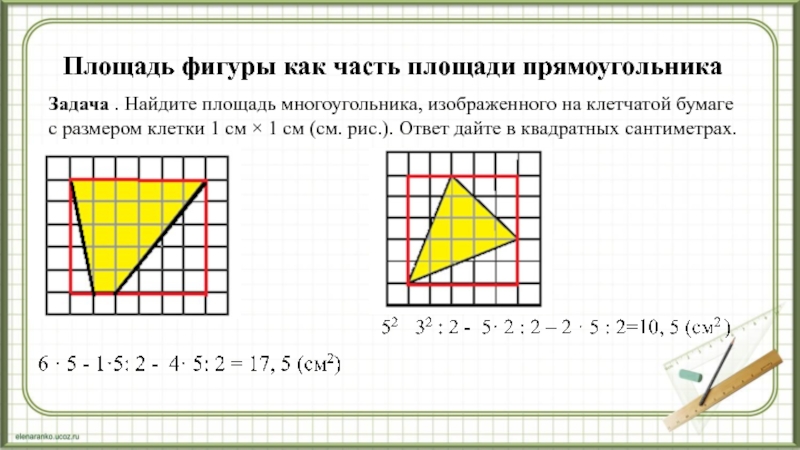
Задача . Найдите площадь многоугольника,
изображенного на клетчатой бумаге с размером клетки 1 см ×
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.Слайд 11
Георг Алекса́ндр Пик ( 10 августа 1859 —13 июля 1942)
— австрийский математик
В 16 лет Георг окончил школу и поступил
в Венский университет. В 20 лет получил право преподавать физику и математику.
16 апреля 1880 года Пик защитил докторскую диссертацию «О классе абелевых интегралов».
В 1900—1901 годах занимал пост декана философского факультета.
Круг математических интересов Пика был чрезвычайно широк. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника.
В Германии эта теорема включена в школьные учебники.
Слайд 12Формула Пика
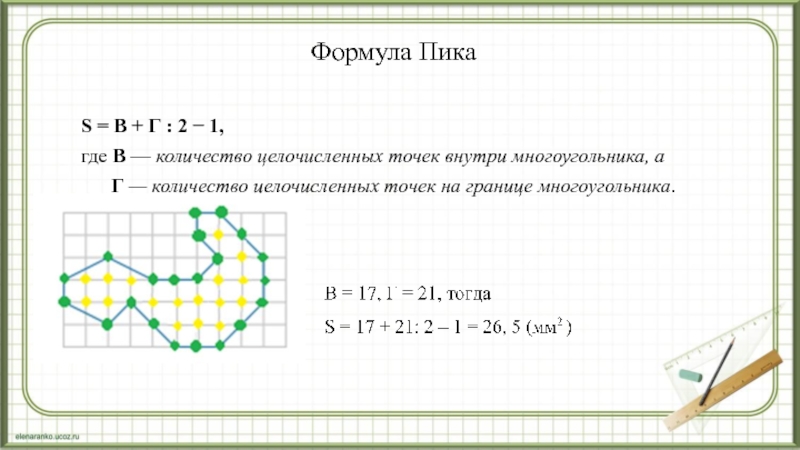
S = В + Г : 2 − 1,
где
В — количество целочисленных точек внутри многоугольника, а
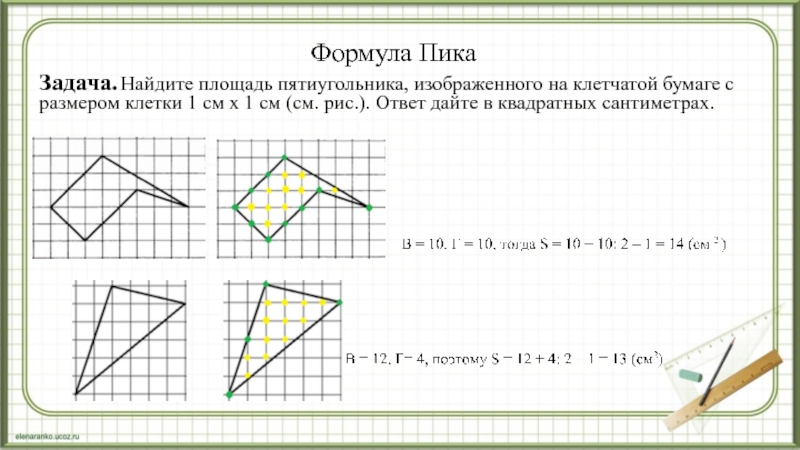
Г — количество целочисленных точек на границе многоугольника.Слайд 13Задача. Найдите площадь пятиугольника, изображенного на клетчатой бумаге с размером
клетки 1 см x 1 см (см. рис.). Ответ дайте
в квадратных сантиметрах.Формула Пика
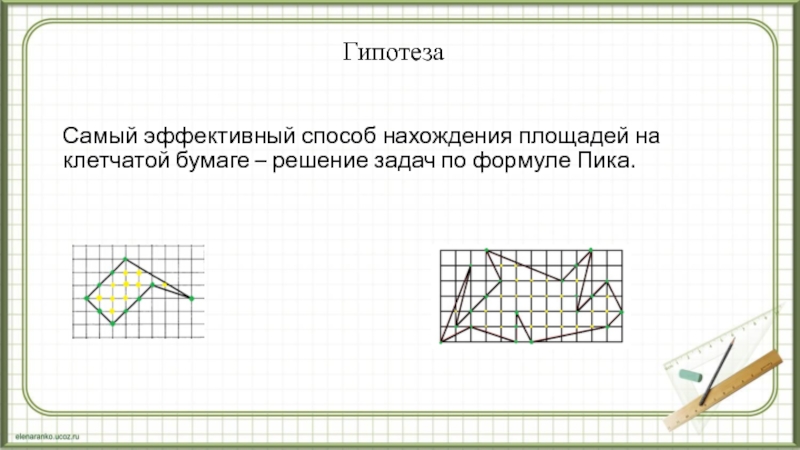
Слайд 15Гипотеза
Самый эффективный способ нахождения площадей на клетчатой бумаге – решение
задач по формуле Пика.
Слайд 18Заключение
Проведенный эксперимент показал, что:
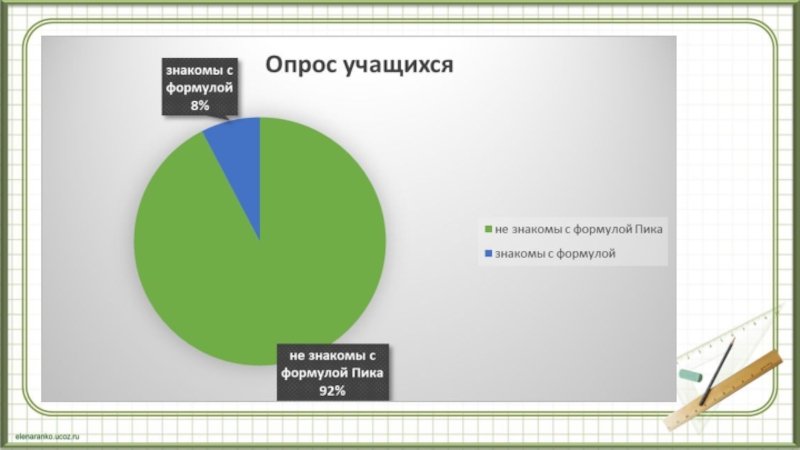
1) ранее семь человек были знакомы
с формулой Пика, но не применяли её на практике;
2) при
решении задач знакомыми способами 47% учеников допустили ошибки; 3) при решении задач, используя формулу Пика, ошибки допустили 26 %, повысив процент выполнения заданий на 21 ;
4) среднее время, затраченное на выполнение заданий, сократилось в 1,6 раза.
Слайд 21Выводы:
В результате работы над данной темой мы выполнили цели
и задачи, которые поставили перед собой. Установили, что все рассмотренные
способы нахождения площадей фигур на клетчатой бумаге интересны, но самым эффективным оказался способ решения по формуле Пика! Наша гипотеза подтвердилась.Задания, представленные в нашей работе, взяты из «Открытого банка заданий по математике» для подготовки к ЕГЭ. Таким образом, подтвердилась актуальность нашей работы, она будет полезна при подготовке к выпускным экзаменам по математике и при нахождении площадей многоугольников.
Слайд 22
Список литературы и источников
1. Википедия. Формула Пика. – [Электронный ресурс]
– URL: https://ru.wikipedia.org/wiki
2. Геометрия и искусство. [Цитаты]. – [Электронный ресурс]
– URL http://geometry-and-art.ru/tsitat.html3. ЕГЭ по Математике (профильный) – [Электронный ресурс] – URL: https://reshimvse.com/mathege/
4. Незнайка — ЕГЭ, ОГЭ, ВПР 2019 – [Электронный ресурс] – URL: https://neznaika.info/q
5. Открытый банк заданий ЕГЭ 2019 по математике. – [Электронный ресурс] – URL: http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege
6. Смирнов В.А., Смирнова И.М., Ященко И.В. Наглядная геометрия. - М., МЦНМО, 2013.
7. Смирнова И. М., Смирнов В. А. Геометрические задачи с практическим содержанием. – М.: Чистые пруды, 2010.
8. Смирнова И. М., Смирнов В. А. Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2009.










![Площади многоугольников на клетчатой бумаге 5 класс Список литературы и источников 1. Википедия. Формула Пика. – [Электронный Список литературы и источников 1. Википедия. Формула Пика. – [Электронный ресурс] – URL: https://ru.wikipedia.org/wiki2. Геометрия и](/img/tmb/5/417916/f47252cab4da4a2024c11b09e580cc45-800x.jpg)