Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация для урока геометрии по теме "Свойства параллельных прямых"
Содержание
- 1. Презентация для урока геометрии по теме "Свойства параллельных прямых"
- 2. Сегодня на уроке ябуду повторять теорему о накрест лежащих углах; доказывать две теоремы;решать задачи.
- 3. Если две параллельные прямые пересечены третьей, то
- 4. Слайд 4
- 5. Доказательство:ABCDMN12ABCDMN12KOПусть прямые АВ и СD параллельны, МN
- 6. Объяснение нового материалаТеорема: Если две параллельные прямые
- 7. Доказательство:2авАВ31Пусть параллельные прямые а и b пересечены
- 8. Теорема: Если две параллельные прямые пересечены секущей,
- 9. Доказательство:Пусть параллельные прямые а и b пересечены
- 10. Упражнения для глаз
- 11. Решение: 1. Пусть Х – это ∠
- 12. Решение: 1. Т.к. ∠4 = 45°, то∠2
- 13. Решение: 1. ∠1=∠2, т.к. они вертикальные,
- 14. Домашнее заданиеВыучить теоремы стр.62
- 15. Сегодня на уроке яповторял теорему о накрест
- 16. Скачать презентанцию
Сегодня на уроке ябуду повторять теорему о накрест лежащих углах; доказывать две теоремы;решать задачи.
Слайды и текст этой презентации
Слайд 1Классная работа
*
Словарь: нак……..т лежа……..е углы, од…………….е у….ы, соо…….е у…..ы
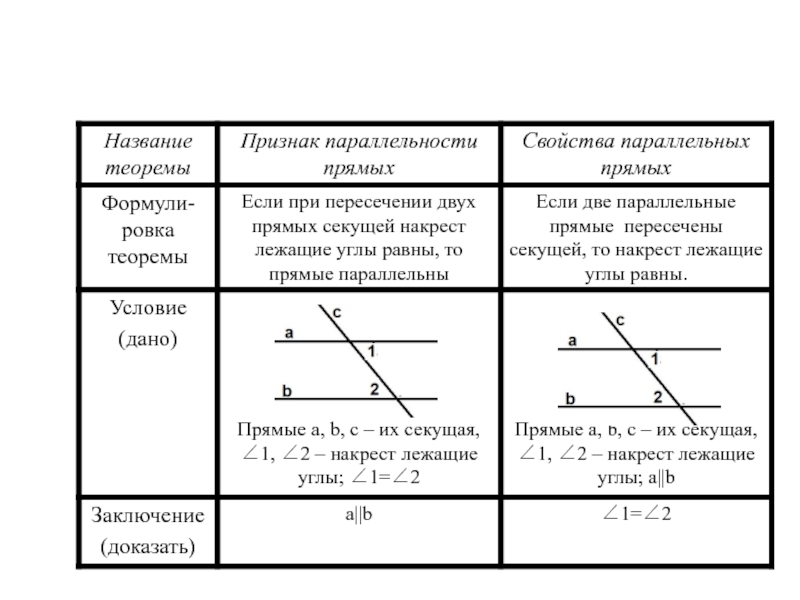
Теорема об
углах, образованных двумя параллельными прямыми и секущей
Слайд 2Сегодня на уроке я
буду повторять теорему о накрест лежащих углах;
доказывать две теоремы;
решать задачи.
Слайд 3Если две параллельные прямые пересечены третьей, то накрест лежащие углы
равны.
Это свойство накрест лежащих углов.
Проверка домашнего задания
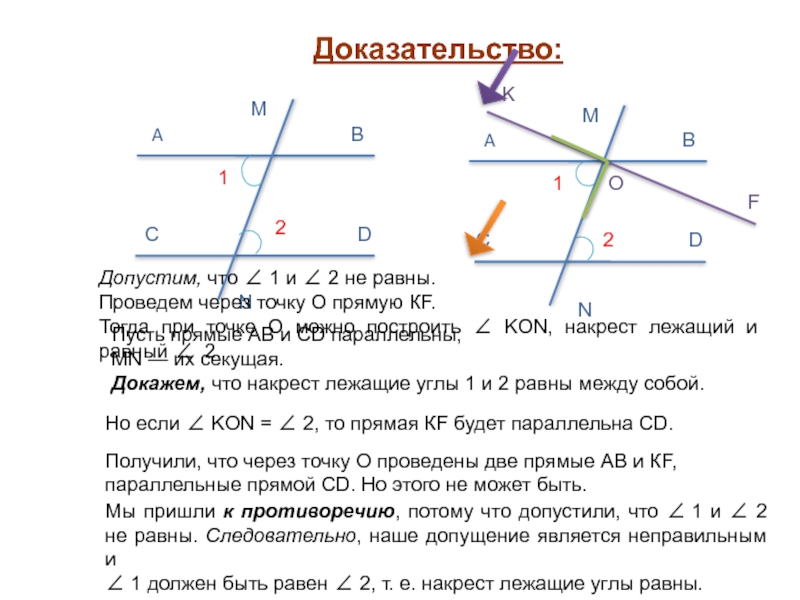
Слайд 5Доказательство:
A
B
C
D
M
N
1
2
A
B
C
D
M
N
1
2
K
O
Пусть прямые АВ и СD параллельны,
МN — их секущая.
Докажем,
что накрест лежащие углы 1 и 2 равны между собой.
Допустим,
что ∠ 1 и ∠ 2 не равны. Проведем через точку О прямую КF.
Тогда при точке О можно построить ∠ KON, накрест лежащий и равный ∠ 2.
Но если ∠ KON = ∠ 2, то прямая КF будет параллельна СD.
Получили, что через точку О проведены две прямые АВ и КF, параллельные прямой СD. Но этого не может быть.
Мы пришли к противоречию, потому что допустили, что ∠ 1 и ∠ 2 не равны. Следовательно, наше допущение является неправильным и
∠ 1 должен быть равен ∠ 2, т. е. накрест лежащие углы равны.
F
Слайд 6
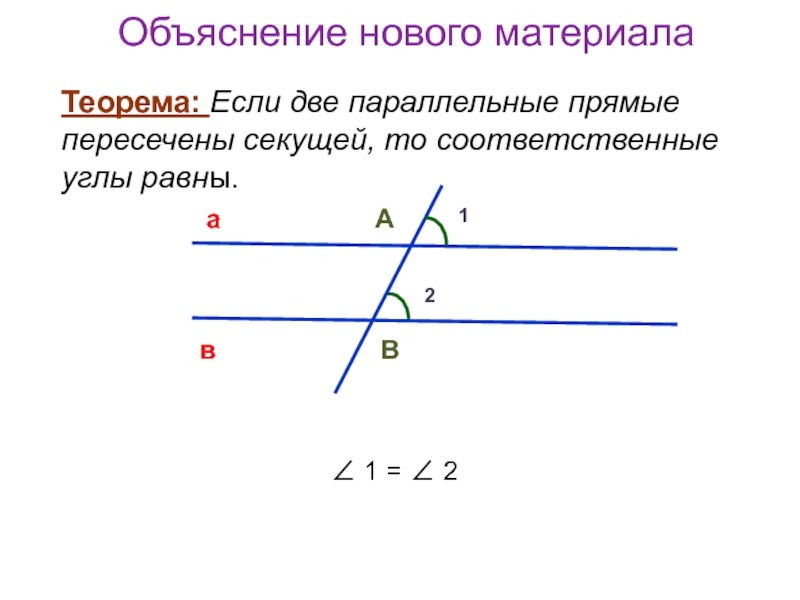
Объяснение нового материала
Теорема: Если две параллельные прямые пересечены секущей, то
соответственные углы равны.
а
в
А
В
1
2
∠ 1 = ∠ 2
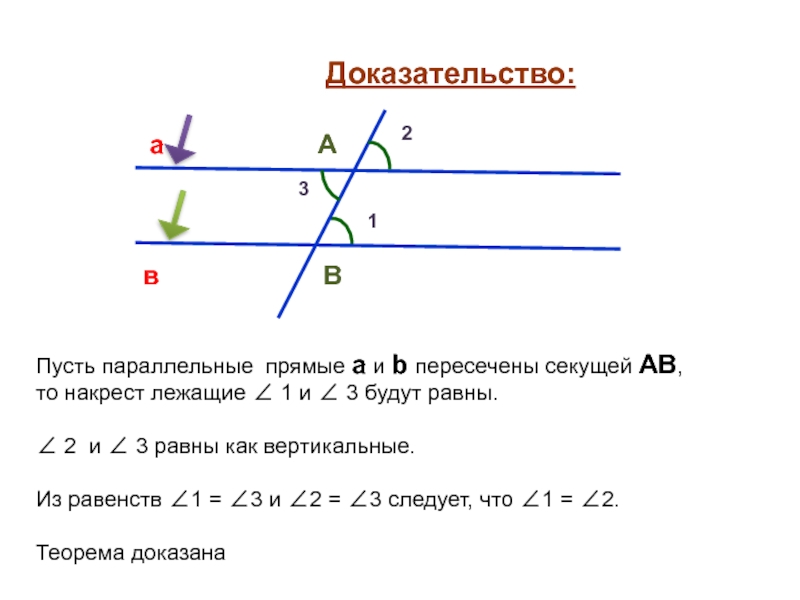
Слайд 7Доказательство:
2
а
в
А
В
3
1
Пусть параллельные прямые а и b пересечены секущей АВ,
то
накрест лежащие ∠ 1 и ∠ 3 будут равны.
∠
2 и ∠ 3 равны как вертикальные.Из равенств ∠1 = ∠3 и ∠2 = ∠3 следует, что ∠1 = ∠2.
Теорема доказана
Слайд 8
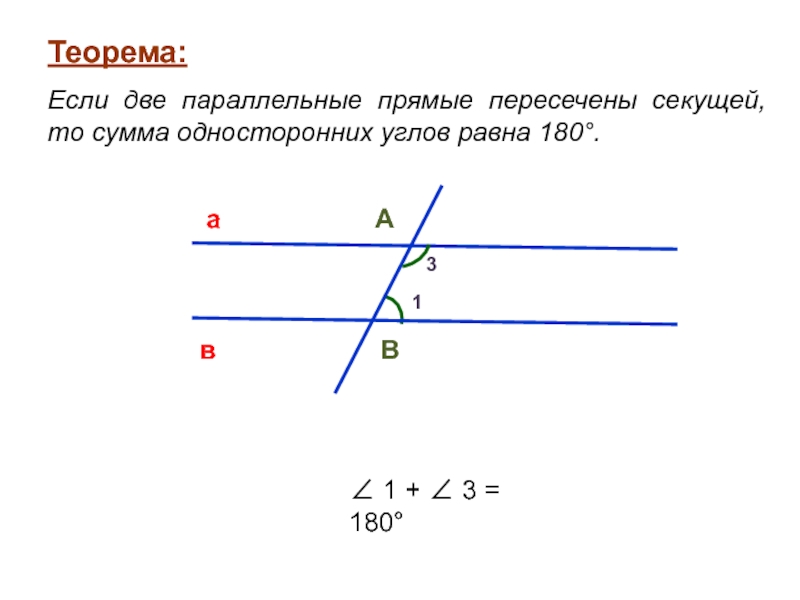
Теорема:
Если две параллельные прямые пересечены секущей, то сумма односторонних
углов равна 180°.
а
в
А
В
3
1
∠ 1 + ∠ 3 = 180°
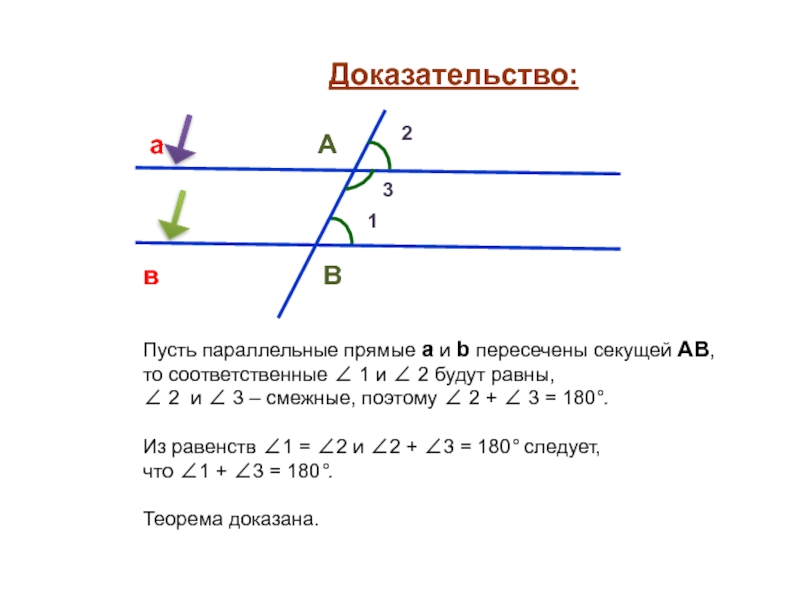
Слайд 9Доказательство:
Пусть параллельные прямые а и b пересечены секущей АВ,
то
соответственные ∠ 1 и ∠ 2 будут равны,
∠ 2
и ∠ 3 – смежные, поэтому ∠ 2 + ∠ 3 = 180°.Из равенств ∠1 = ∠2 и ∠2 + ∠3 = 180° следует,
что ∠1 + ∠3 = 180°.
Теорема доказана.
2
а
в
А
В
3
1
Слайд 11Решение:
1. Пусть Х – это ∠ 2, тогда ∠
1 = (Х+70°),
т.к. сумма углов 1 и
2 = 180°, в силу того, что они смежные.
Составим уравнение:
Х+ (Х+70°) = 180°
2Х = 110 °
Х = 55° (Угол 2)
2. Найдем ∠ 1.
55° + 70° = 125°
3. ∠ 1 = ∠ 3, т.к. они вертикальные.
∠ 3 = ∠ 5, т.к. они
накрест лежащие. 125°
∠ 5 = ∠ 7, т.к. они вертикальные.
∠ 2 = ∠ 4, т.к. они вертикальные.
∠ 4 = ∠ 6, т.к. они
накрест лежащие. 55°
∠ 6 = ∠ 8, т.к. они вертикальные.
Задача №1:
A
B
C
4
3
5
8
7
2
1
6
Условие: найдите все углы, образованные при пересечении двух параллельных A и B секущей C, если один из углов на 70° больше другого.
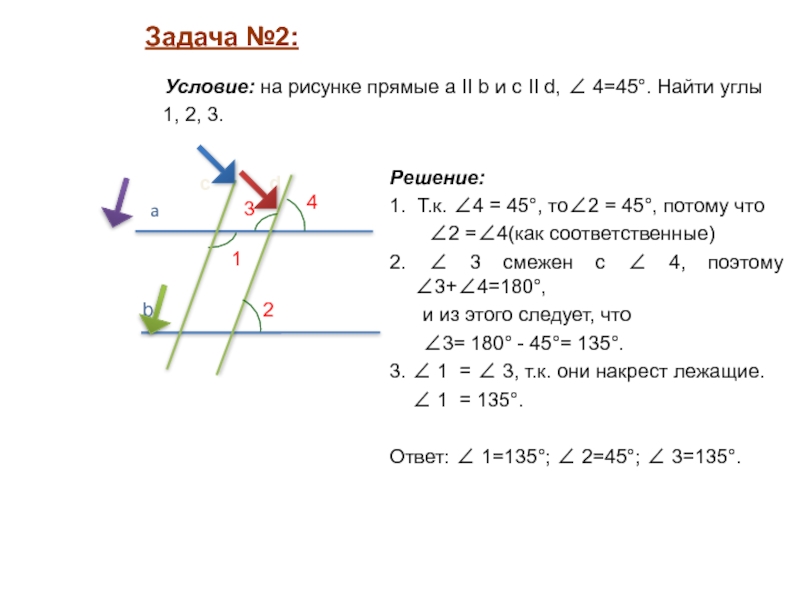
Слайд 12Решение:
1. Т.к. ∠4 = 45°, то∠2 = 45°, потому
что
∠2 =∠4(как соответственные)
2. ∠ 3
смежен с ∠ 4, поэтому ∠3+∠4=180°,и из этого следует, что
∠3= 180° - 45°= 135°.
3. ∠ 1 = ∠ 3, т.к. они накрест лежащие.
∠ 1 = 135°.
Ответ: ∠ 1=135°; ∠ 2=45°; ∠ 3=135°.
Задача №2:
a
b
d
1
Условие: на рисунке прямые а II b и c II d, ∠ 4=45°. Найти углы 1, 2, 3.
c
3
2
4
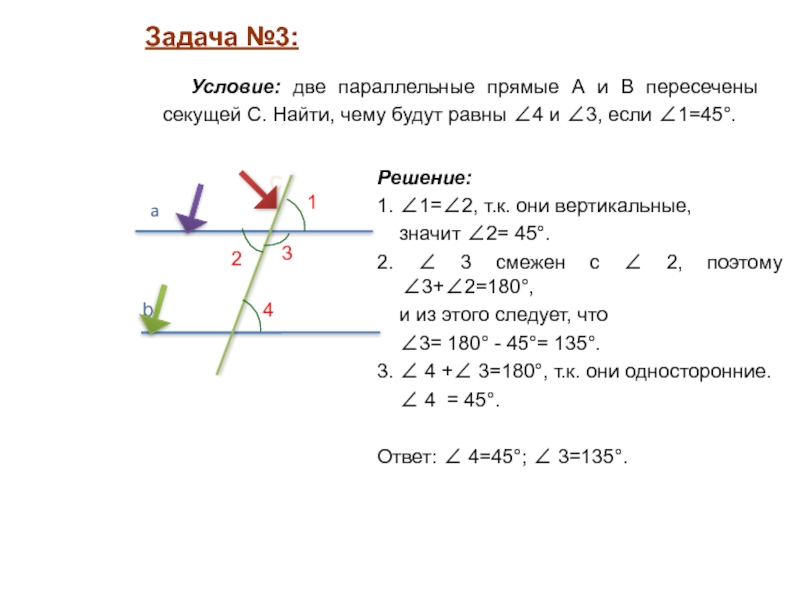
Слайд 13Решение:
1. ∠1=∠2, т.к. они вертикальные,
значит ∠2=
45°.
2. ∠ 3 смежен с ∠ 2, поэтому ∠3+∠2=180°,
и из этого следует, что ∠3= 180° - 45°= 135°.
3. ∠ 4 +∠ 3=180°, т.к. они односторонние.
∠ 4 = 45°.
Ответ: ∠ 4=45°; ∠ 3=135°.
Задача №3:
a
b
С
2
Условие: две параллельные прямые А и B пересечены секущей С. Найти, чему будут равны ∠4 и ∠3, если ∠1=45°.
3
4
1
Слайд 15Сегодня на уроке я
повторял теорему о накрест лежащих углах;
доказывал
Теоремы об углах, образованных двумя параллельными прямыми и секущей;
решал задачи.
