Решение текстовых задач на смеси, сплавы, растворы

Содержание

1. Решение текстовых задач на смеси, сплавы, растворы
2. 1. Смешали 30 % раствор
3. Слайд 3
4. 0,3х + 0,1(600 – х) = 0,15
5. 2. Бронза является сплавом меди и
6. Слайд 6
7. 96*1/12 + х*1/10 = (96 + х)1/11,8
8. 3. Имеется два сплава с
9. 1,5 : 5 = 0, 3.Ответ: 0,3.
10. 4. У хозяйки есть 5 л сахарного
11. Слайд 11
12. (5 + х) 0,2 = 2,5,1 +
13. Имеется два сплава меди и свинца. Один
14. Слайд 14
15. Слайд 15
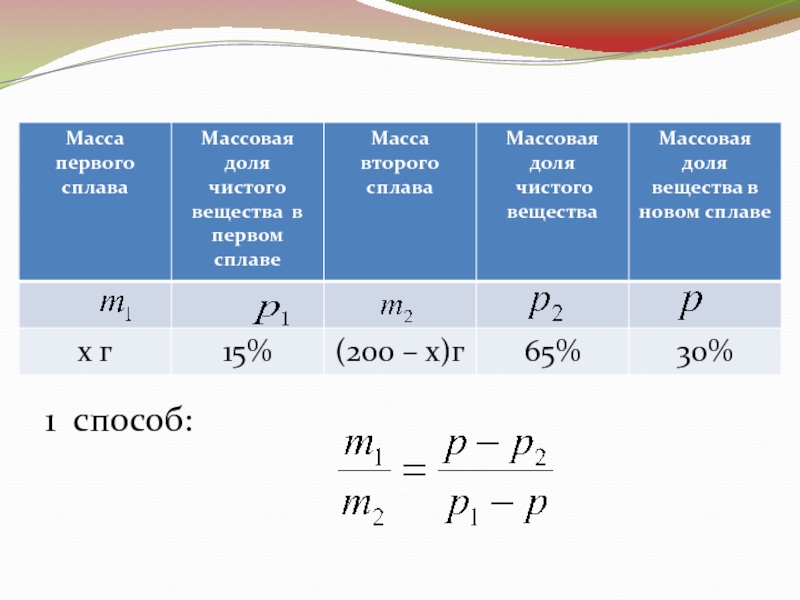
16. 1 способ:
17. 2 способ:0,15х + 0,65(200 – х) =
18. Имелось два сплава серебра. Процент содержания
19. Источник информации: Сайт ФИПИhttp://85.142.162.119/os11/xmodules/qprint/index.php?theme_guid=2ef483029541e311b90c001fc68344c9&proj_guid=AC437B34557F88EA4115D2F374B0A07B
20. Скачать презентанцию

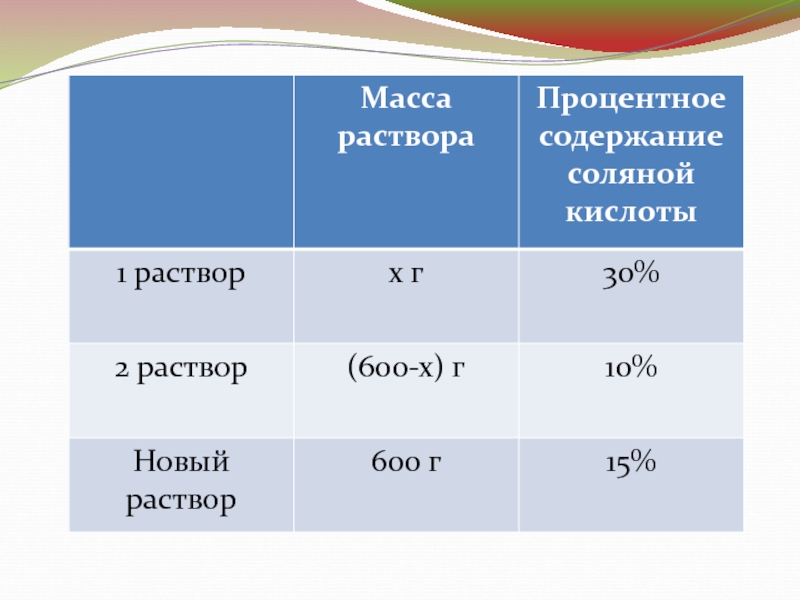
1. Смешали 30 % раствор соляной кислоты с 10 % и получили 600 г 15 % раствора. Сколько граммов первого раствора было взято?

Главная
Математика
Решение текстовых задач на смеси, сплавы, растворы

Слайды и текст этой презентации

Слайд 1 Решение текстовых задач на смеси, сплавы, растворы
Материал подготовлен
учителем математики

МБОУ «Теньковская СОШ»
Назарычевой М. А.

2017 год

Решение текстовых задач на смеси, сплавы, растворыМатериал подготовлен учителем математики МБОУ «Теньковская СОШ»

Слайд 2 1. Смешали 30 % раствор соляной кислоты с

10 % и получили 600 г

15 % раствора. Сколько граммов первого раствора было взято?

1. Смешали 30 % раствор соляной кислоты с 10 % и получили 600

Слайд 40,3х + 0,1(600 – х) = 0,15 х 600,

0,3х +

60 – 0,1х = 90,

0,2х = 30,

х = 150 (г)

–первого раствора было взято.
Ответ: 150.

0,3х + 0,1(600 – х) = 0,15 х 600,0,3х + 60 – 0,1х = 90,0,2х = 30,х

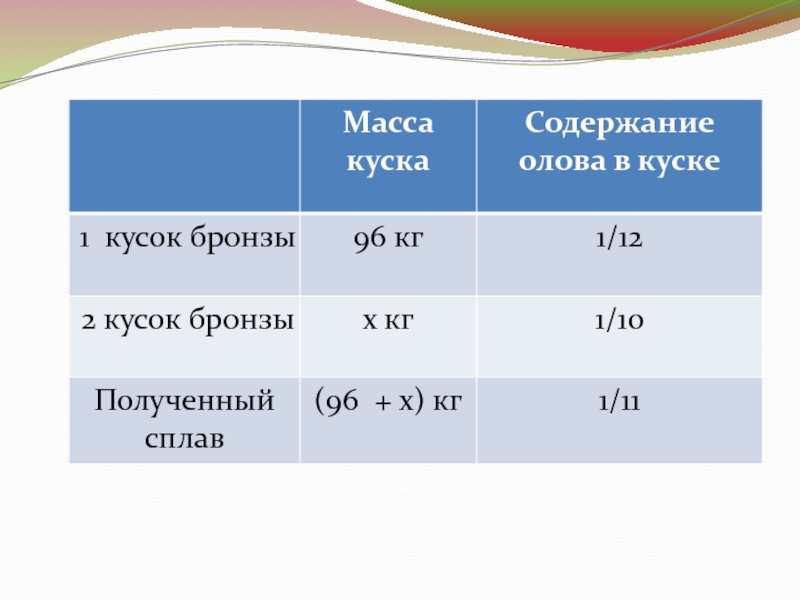
Слайд 52. Бронза является сплавом меди и олова (в разных

пропорциях). Кусок бронзы весом 96 кг, содержащий 1/12

часть олова, сплавили с другим куском, содержащим 1/10 часть олова. Сколько килограмм весит второй кусок, если полученный сплав содержит 1/11 часть олова?

2. Бронза является сплавом меди и олова (в разных пропорциях). Кусок бронзы весом 96 кг, содержащий

Слайд 7

961/12 + х1/10 = (96 + х)1/11,
8 + 0,1х =

1/11х + 96/11,
1/10х – 1/11х = 96/11 – 88/11,
11/110х -

10/110х = 8/11,
1/110х = 8/11,
х = 8/11: 1/110,
х = 80(кг)-весит второй кусок.

Ответ: 80.

96*1/12 + х*1/10 = (96 + х)1/11,8 + 0,1х = 1/11х + 96/11,1/10х – 1/11х = 96/11

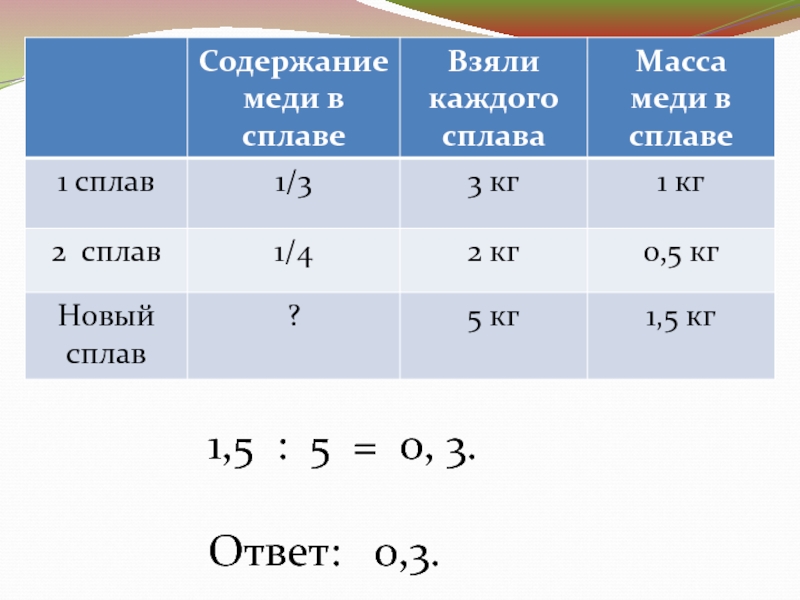
Слайд 83. Имеется два сплава с разным содержанием меди:

в первом содержится 1/3, а во втором – ¼ меди.

Сплавили 3 кг первого и 2 кг второго сплава. Какую часть меди содержит новый сплав?

3. Имеется два сплава с разным содержанием меди: в первом содержится 1/3, а во втором

Слайд 91,5 : 5 = 0, 3.

Ответ: 0,3.

Слайд 104. У хозяйки есть 5 л сахарного сиропа 50% концентрации.

Сколько литров воды необходимо добавить для получения сиропа 20% концентрации?

4. У хозяйки есть 5 л сахарного сиропа 50% концентрации. Сколько литров воды необходимо добавить для получения

Слайд 12(5 + х) 0,2 = 2,5,
1 + 0,2х = 2,5,
0,2х

= 1,5,
х = 1,5 : 0,2,
х = 7,5(л) - воды

необходимо добавить для получения сиропа 20% концентрации.
Ответ: 7,5.

(5 + х) 0,2 = 2,5,1 + 0,2х = 2,5,0,2х = 1,5,х = 1,5 : 0,2,х =

Слайд 13Имеется два сплава меди и свинца. Один сплав содержит 15%

меди, а другой 65% меди. Сколько нужно взять первого сплава,

чтобы получить 200 г сплава, содержащего 30% меди?

Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди. Сколько нужно

Слайд 161 способ:

Слайд 172 способ:
0,15х + 0,65(200 – х) = 0,3*200,

0,15х + 130

– 0,65х = 60,

0,5х = - 70,

х = 140(г) –

первого сплава нужно взять.

Ответ: 140.

2 способ:0,15х + 0,65(200 – х) = 0,3*200,0,15х + 130 – 0,65х = 60,0,5х = - 70,х

Слайд 18 Имелось два сплава серебра. Процент содержания серебра в первом

сплаве был на 25% выше, чем во втором. Когда сплавили

их вместе, то получили сплав, содержащий 30% серебра. Определить массы сплавов, если известно, что серебра в первом сплаве было 4кг, а во втором 8 кг. Ответ: 8 кг; 32 кг
В первом сосуде растворили 0,36 л, а во втором 0,42 л чистого спирта. Процентное содержание спирта в первом сосуде оказалось на 6% больше, чем во втором. Каково процентное содержание спирта во втором и первом сосудах, если известно, что растворы в первом сосуде на 4 л меньше? Ответ: 12% и 6%
В 4 кг сплава меди и олова содержится 40% олова. Сколько килограммов олова добавить к этому сплаву, чтобы его процентное содержание в новом сплаве стало бы равным 70%? Ответ: 4кг
К 40% раствору серной кислоты добавили 50 г чистой серной кислоты, после чего концентрация раствора стала равной 60%. Найти первоначальную массу раствора. Ответ: 100 г
К раствору, содержащему 30 г соли, добавили 400 г, после чего концентрация соли уменьшилась на 10%. Найти первоначальную концентрацию соли в растворе. Ответ: 15%
В 5 кг сплава олова и цинка содержится 80% цинка. Сколько килограммов олова надо добавить к сплаву, чтобы процентное содержание цинка стало вдвое меньше? Ответ: 5 кг