Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сумма углов в треугольнике
Содержание
- 1. Сумма углов в треугольнике
- 2. СУММА УГЛОВ ТРЕУГОЛЬНИКАЗадание 1. С помощью транспортира найдите сумму углов следующих треугольников,GВСDEFАHJKLM
- 3. СУММА УГЛОВ ТРЕУГОЛЬНИКАЗадание 2. Результаты исследований занесите в таблицу.
- 4. СУММА УГЛОВ ТРЕУГОЛЬНИКАЗадание 3. Проверьте. Сформулируйте вывод. Сумма углов треугольника равна 180°
- 5. ТЕОРЕМА 4.4 О СУММЕ УГЛОВ ТРЕУГОЛЬНИКАСумма
- 6. Теорема о сумме углов треугольникаВСDAДано: треугольник АВС.Доказать:
- 7. Теорема о сумме углов треугольника2. Рассмотрим параллельные
- 8. Теорема о сумме углов треугольника3. Рассмотрим параллельные
- 9. ВЫПОЛНИТЕ ЗАДАНИЕНайти третий угол треугольника, если два
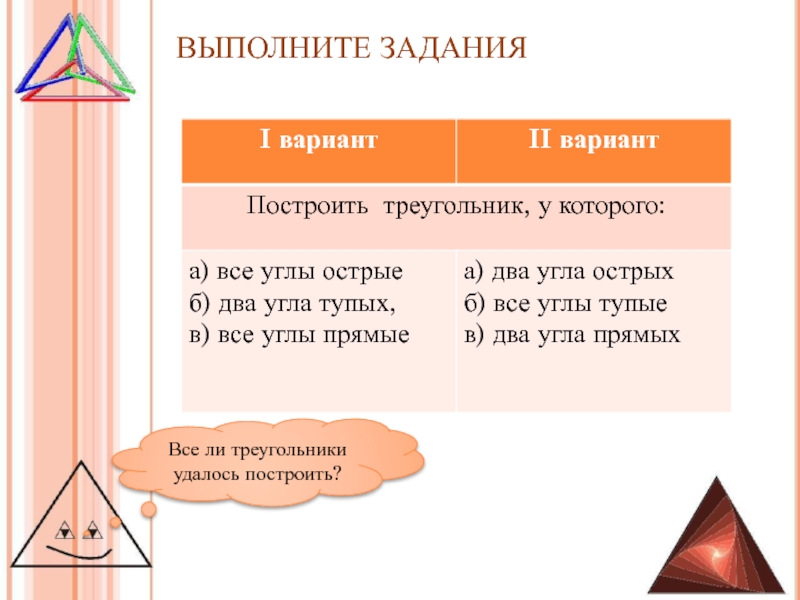
- 10. ВЫПОЛНИТЕ ЗАДАНИЯВсе ли треугольники удалось построить?
- 11. ВЫПОЛНИТЕ ЗАДАНИЯ1. Найдите величину неизвестного угла треугольника. 6460?АВСEDFGHI??KLMN1208040
- 12. ВЫПОЛНИТЕ ЗАДАНИЯ2. По результатам вычислений заполните таблицу.3.
- 13. Следствия из теоремы о сумме углов треугольника 1.
- 14. Из истории геометрии Геродот, (484 до н. э.
- 15. Из истории геометрии Треугольник всегда
- 16. Из истории геометрии Среди "определений",
- 17. ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА:Виленкин Н.Я., Депман И.Я. За страницами
- 18. Скачать презентанцию
СУММА УГЛОВ ТРЕУГОЛЬНИКАЗадание 1. С помощью транспортира найдите сумму углов следующих треугольников,GВСDEFАHJKLM
Слайды и текст этой презентации
Слайд 1СУММА УГЛОВ ТРЕУГОЛЬНИКА
Демонстрационный материал к уроку геометрии в 7 классе
Автор:
Смирнова Елена Андреевна,
г. Саратова
Слайд 2СУММА УГЛОВ ТРЕУГОЛЬНИКА
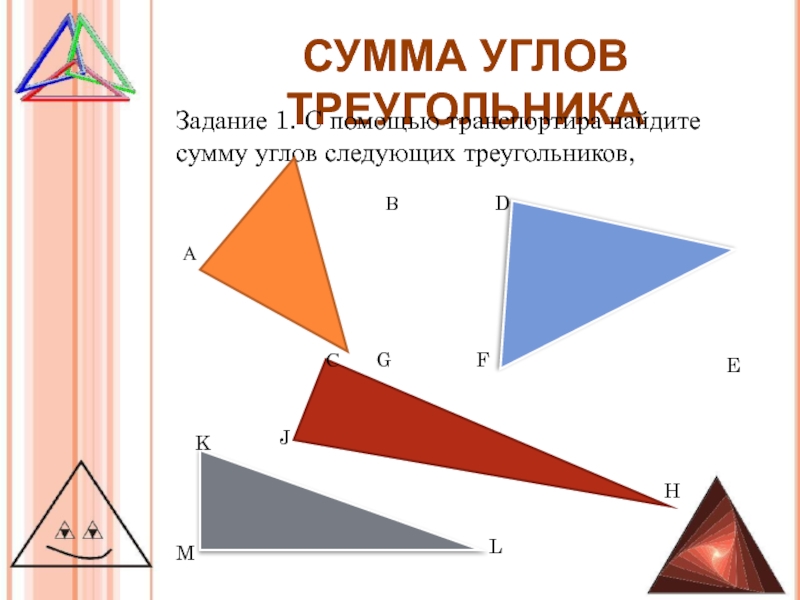
Задание 1. С помощью транспортира найдите сумму углов
следующих треугольников,
G
В
С
D
E
F
А
H
J
K
L
M
Слайд 4СУММА УГЛОВ ТРЕУГОЛЬНИКА
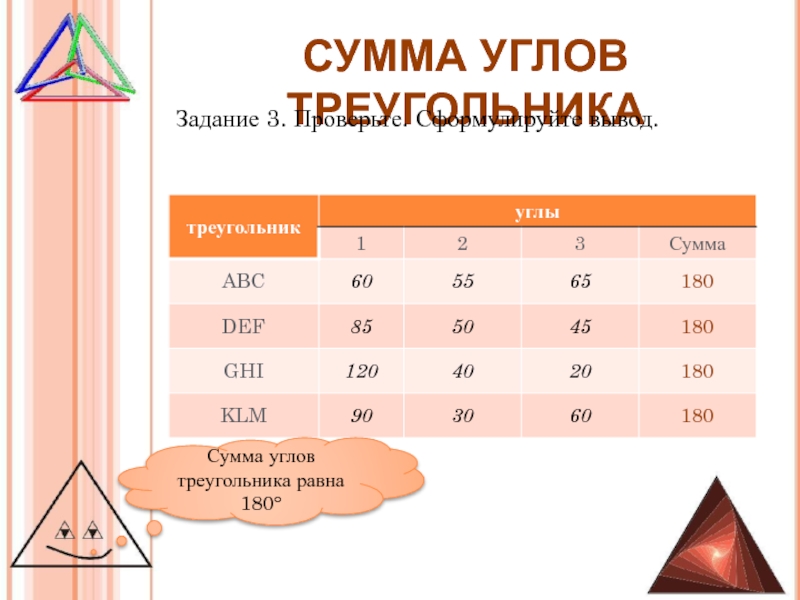
Задание 3. Проверьте. Сформулируйте вывод.
Сумма углов треугольника
равна 180°
Слайд 5ТЕОРЕМА 4.4
О СУММЕ УГЛОВ ТРЕУГОЛЬНИКА
Сумма углов треугольника равна 180°
Идея
доказательства: свести к известной теореме, в которой фигурирует равенство угла
180°.Сформулируйте эту теорему!...
Слайд 6Теорема о сумме углов треугольника
В
С
D
A
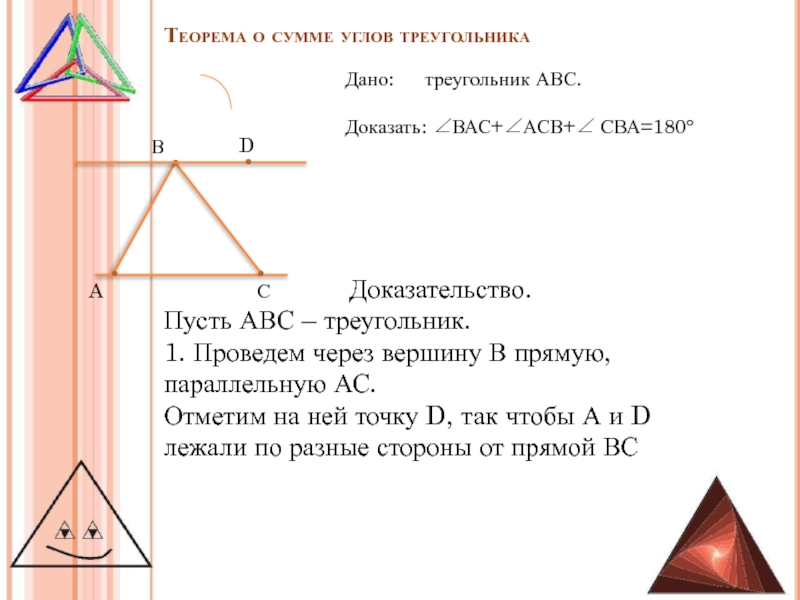
Дано: треугольник АВС.
Доказать: ∠ВАС+∠АСВ+∠ СВА=180°
Доказательство.
Пусть АВС
– треугольник.
1. Проведем через вершину В прямую, параллельную АС.
Отметим на
ней точку D, так чтобы А и D лежали по разные стороны от прямой ВС
Слайд 7Теорема о сумме углов треугольника
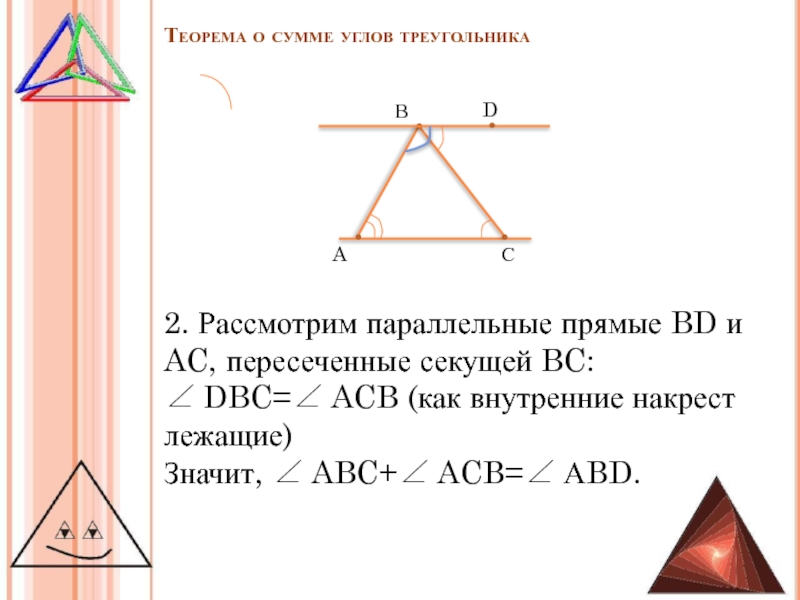
2. Рассмотрим параллельные прямые BD и
AC, пересеченные секущей BC:
∠ DBC=∠ ACB (как внутренние накрест лежащие)
Значит,
∠ ABC+∠ ACB=∠ АBD.В
С
D
A
Слайд 8Теорема о сумме углов треугольника
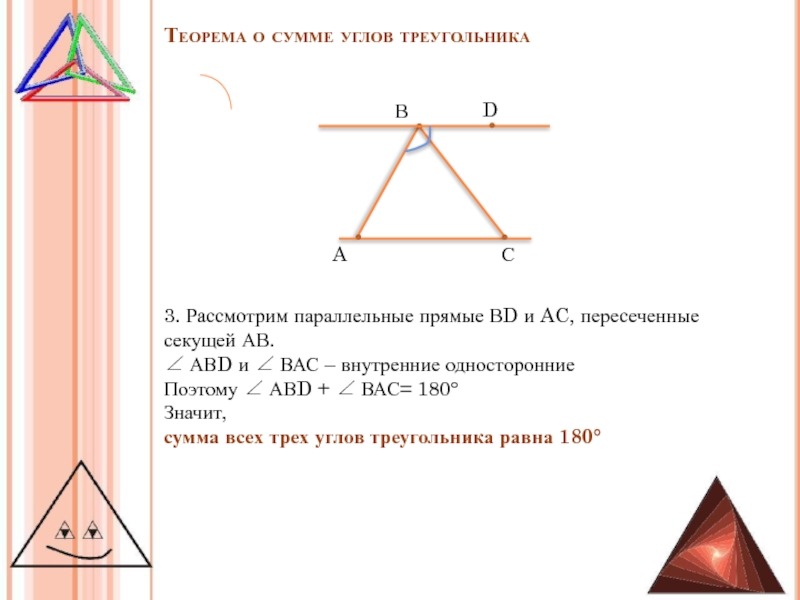
3. Рассмотрим параллельные прямые ВD и
AC, пересеченные секущей АВ.
∠ АВD и ∠ ВАС – внутренние
односторонниеПоэтому ∠ АВD + ∠ ВАС= 180°
Значит,
сумма всех трех углов треугольника равна 180°
В
С
D
A
Слайд 9ВЫПОЛНИТЕ ЗАДАНИЕ
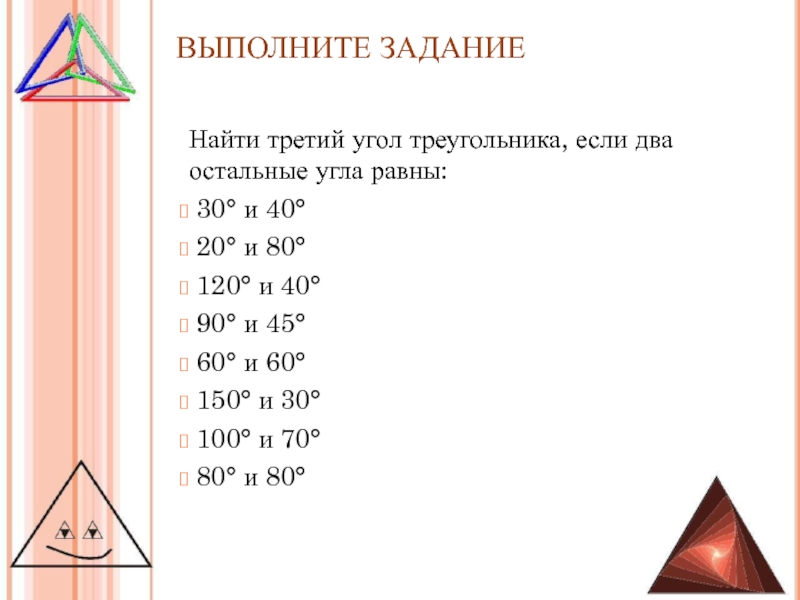
Найти третий угол треугольника, если два остальные угла равны:
30° и 40°
20° и 80°
120° и 40°
90°
и 45°60° и 60°
150° и 30°
100° и 70°
80° и 80°
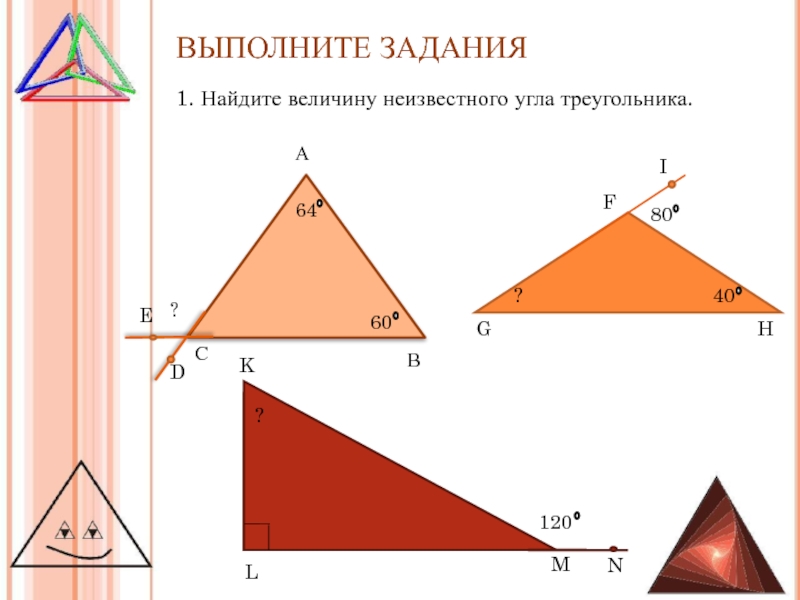
Слайд 11ВЫПОЛНИТЕ ЗАДАНИЯ
1. Найдите величину неизвестного угла треугольника.
64
60
?
А
В
С
E
D
F
G
H
I
?
?
K
L
M
N
120
80
40
Слайд 12ВЫПОЛНИТЕ ЗАДАНИЯ
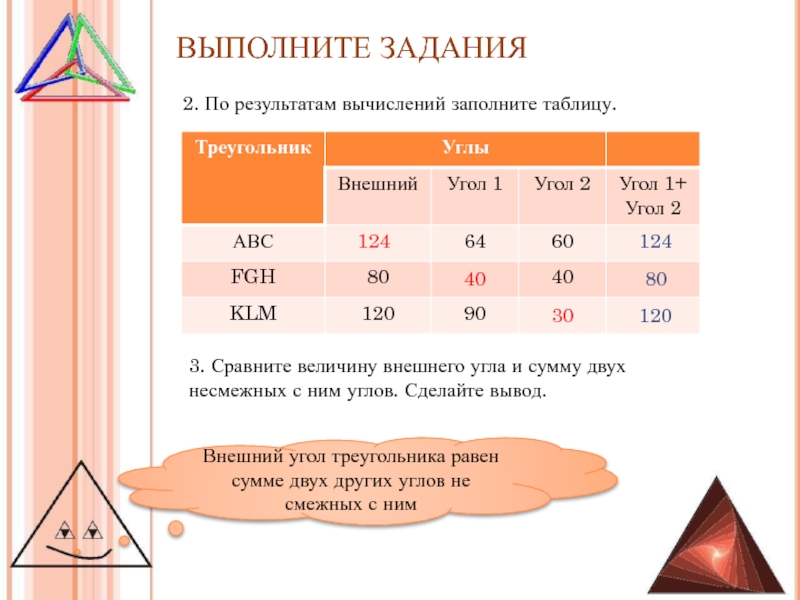
2. По результатам вычислений заполните таблицу.
3. Сравните величину внешнего
угла и сумму двух
несмежных с ним углов. Сделайте вывод.
Внешний
угол треугольника равен сумме двух других углов не смежных с ним124
40
30
124
80
120
Слайд 13Следствия из теоремы о сумме углов треугольника
1. У любого треугольника
хотя бы два угла острые.
2. Внешний угол треугольника равен сумме
двух других углов не смежных с ним.Подумайте, как это можно доказать!
Слайд 14Из истории геометрии
Геродот,
(484 до н. э. — 425 до
н. э.)
Крупнейший древнегреческий историк Геродот (V век
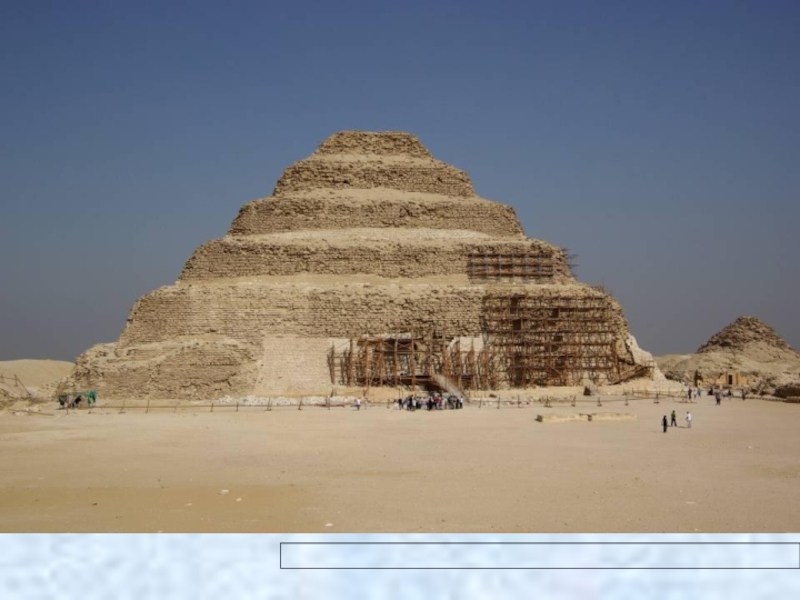
до нашей эры) оставил описание того, как египтяне после каждого разлива Нила заново размечали плодородные участки его берегов, с которых ушла вода. По Геродоту, с этого и началась геометрия – "землемерие" (от греческого "гео" – "земля" и "метрео" – "измеряю").Древние землемеры выполняли геометрические построения, измеряли длины и площади; астрологи рассчитывали расположение небесных светил – все это требовало весьма обширных познаний о свойствах плоских и пространственных фигур, и в первую очередь о треугольнике.
Слайд 15Из истории геометрии
Треугольник всегда имел широкое применение
в практической жизни. Так, в строительном искусстве испокон веков используется
свойство жесткости треугольника для укрепления различных строений и их деталей. Изображение треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и других древних документах.В древней Греции учение о треугольнике развивалось в ионийской школе, основанной в VII веке до нашей эры Фалесом, в школе Пифагора и других; оно было затем полностью изложено в первой книге "Начал" Евклида.
Фалес,
(640/624 — 548/545 до н. э.)
Пифагор,
(570—490 гг. до н. э.)
Слайд 16Из истории геометрии
Среди "определений", которыми начинается эта
книга, имеются и следующие: "Из трехсторонних фигур равносторонний треугольник есть
фигура, имеющая три равные стороны, равнобедренный же – имеющая только две равные стороны, разносторонний – имеющая три неравные стороны". Понятие о треугольнике исторически развивалось, по-видимому, так: сначала рассматривались лишь правильные, затем равнобедренные и, наконец, разносторонние треугольники.Понятие о треугольнике исторически развивалось, по-видимому, так: сначала рассматривались лишь правильные, затем равнобедренные и, наконец, разносторонние треугольники.
Слайд 17ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА:
Виленкин Н.Я., Депман И.Я. За страницами учебника математики. –
М.: Просвещение, 1989.
Глейзер Г.И. История математики в школе. –
М.: Просвещение, 1982.Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия: Учебное пособие для учащихся V – VI классов. – М.: МИРОС, 1995.
