Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Угол между прямыми. Угол между прямой и плоскостью
Содержание
- 1. Угол между прямыми. Угол между прямой и плоскостью
- 2. Две пересекающиеся прямые в пространстве определяют единственную
- 3. ABCD1A1C1Пример 1. Дан куб ABCDA1B1C1D1. Найдите углы
- 4. В общем случае, для нахождения угла между
- 5. Определение. Углом между скрещивающимися прямыми называется угол
- 6. ABCD1A1C1Пример 3. Дан куб ABCDA1B1C1D1. Найдите углы
- 7. Задание. Докажите, что все скрещивающиеся ребра правильной
- 8. Определение. Углом между плоскостью и пересекающей её
- 9. ACD1A1Пример 4. Дан куб ABCDA1B1C1D1. Найдите углы
- 10. Слайд 10
- 11. Слайд 11
- 12. Скачать презентанцию
Две пересекающиеся прямые в пространстве определяют единственную плоскость, поэтому угол между пересекающимися прямыми в пространстве определяется так же как в плоскости. Вспомним это определение:авМОпределение . Меньший из неразвернутых углов, полученных при
Слайды и текст этой презентации
Слайд 2
Две пересекающиеся прямые в пространстве определяют единственную плоскость, поэтому угол
между пересекающимися прямыми в пространстве определяется так же как в
плоскости. Вспомним это определение:а
в
М
Определение . Меньший из неразвернутых углов, полученных при пересечении двух прямых, называется углом между данными прямыми.
Из определения следует, что угол между двумя пересекающимися прямыми не может превышать 900 т.е.
Если прямые параллельные, то величина угла между ними считается равной 00.
Слайд 3
A
B
C
D1
A1
C1
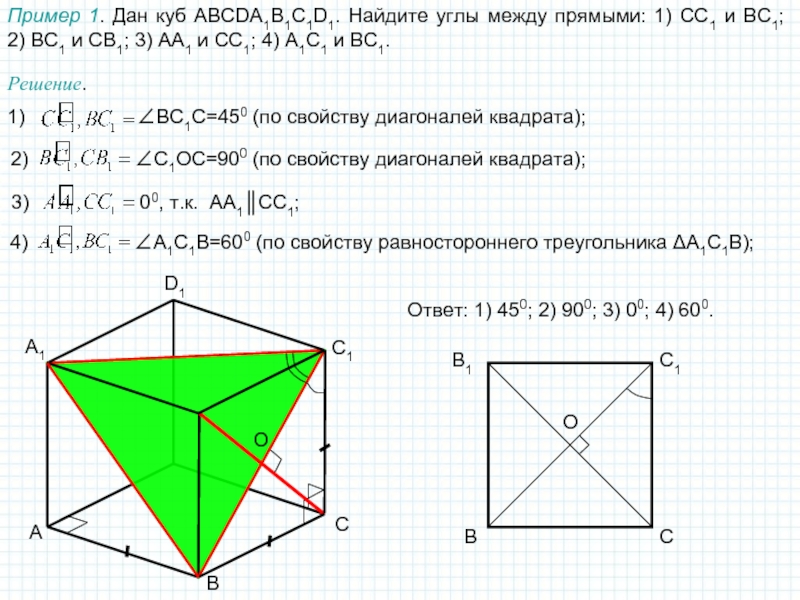
Пример 1. Дан куб ABCDA1B1C1D1. Найдите углы между прямыми: 1)
CC1 и BC1; 2) BC1 и CB1; 3) AA1
и CC1; 4) A1C1 и BC1.B
C
C1
В1
О
О
Ответ: 1) 450; 2) 900; 3) 00; 4) 600.
Слайд 4В общем случае, для нахождения угла между пересекающимися прямыми обычно
рассматривают треугольник, в который входит интересующий нас угол. В прямоугольном
треугольнике необходимо выразить какую-либо тригонометрическую функцию этого угла, в произвольном треугольнике – косинус данного угла (по следствию из теоремы косинусов). Далее сам угол находят с помощью обратных тригонометрических функций.Пример 2. Дан прямоугольный параллелепипед ABCDA1B1C1D1, AB=4 см, ВС=3 см, ВВ1=2 см. Найдите углы между прямыми: 1) CC1 и BC1; 2) BC1 и CB1; 3) AA1 и CC1; 3) A1C1 и BC1.
О
Слайд 5
Определение. Углом между скрещивающимися прямыми называется угол между соответственно параллельными
им пересекающимися прямыми:
а
в
в'
T
a, b⊄, b║b', T∈a, b'
Обратите внимание,
что плоскость, образованная пересекающимися прямыми a и b′ параллельна прямой b (по признаку параллельности прямой и плоскости).
Слайд 6A
B
C
D1
A1
C1
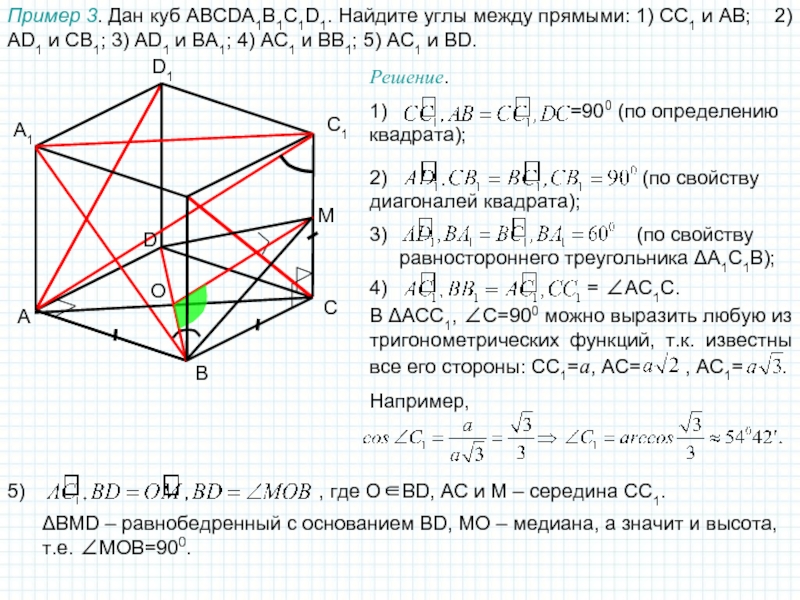
Пример 3. Дан куб ABCDA1B1C1D1. Найдите углы между прямыми: 1)
CC1 и АB; 2) AD1 и CB1; 3) AD1
и BA1; 4) AC1 и BB1; 5) AC1 и BD.O
M
ΔBMD – равнобедренный с основанием BD, МО – медиана, а значит и высота, т.е. ∠MOB=900.
D
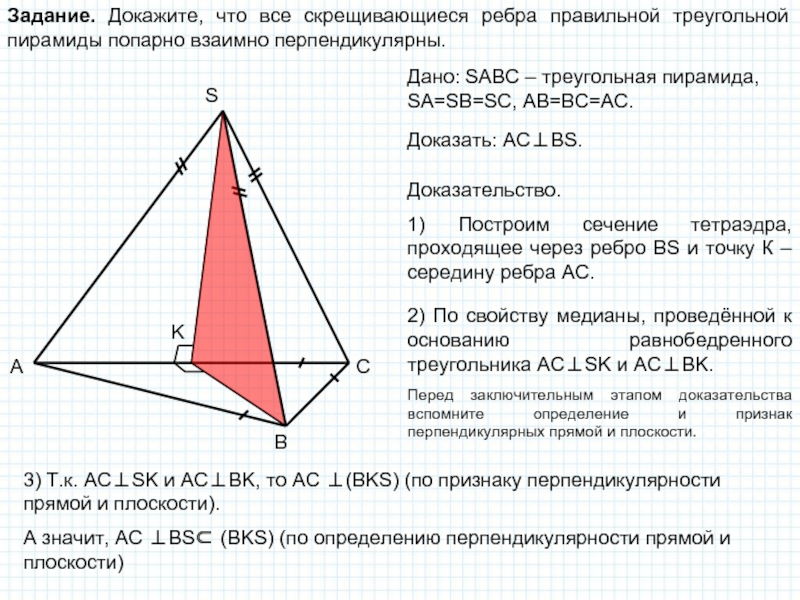
Слайд 7Задание. Докажите, что все скрещивающиеся ребра правильной треугольной пирамиды попарно
взаимно перпендикулярны.
A
B
C
S
K
Дано: SABC – треугольная пирамида, SA=SB=SC, AB=BC=AC.
Доказать: AC⊥BS.
Доказательство.
1) Построим
сечение тетраэдра, проходящее через ребро BS и точку К – середину ребра АС.2) По свойству медианы, проведённой к основанию равнобедренного треугольника АС⊥SK и AC⊥BK.
3) Т.к. АС⊥SK и AC⊥BK, то АС ⊥(BKS) (по признаку перпендикулярности прямой и плоскости).
А значит, АС ⊥BS⊂ (BKS) (по определению перпендикулярности прямой и плоскости)
Перед заключительным этапом доказательства вспомните определение и признак перпендикулярных прямой и плоскости.
Слайд 8
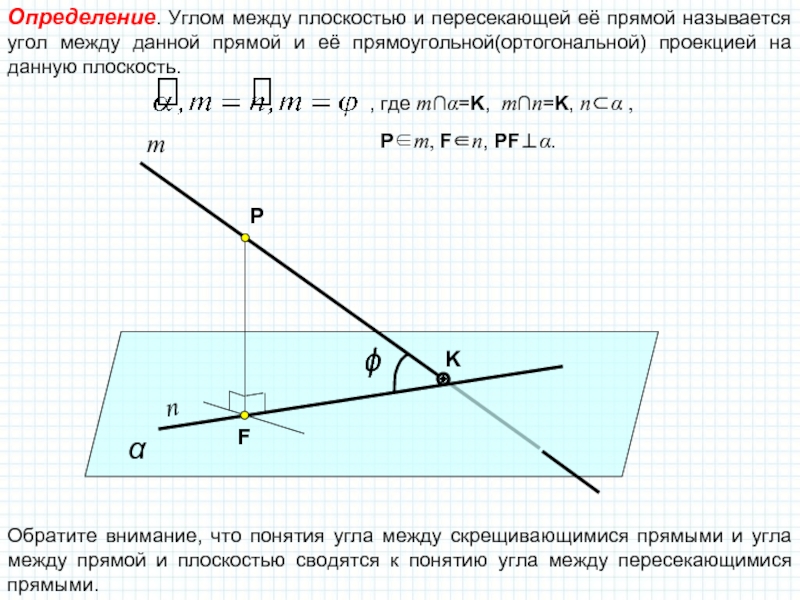
Определение. Углом между плоскостью и пересекающей её прямой называется угол
между данной прямой и её прямоугольной(ортогональной) проекцией на данную плоскость.
т
α
n
K
,
где m∩α=K, m∩n=K, n⊂α , P∈m, F∈n, PF⊥α.
ϕ
P
F
Обратите внимание, что понятия угла между скрещивающимися прямыми и угла между прямой и плоскостью сводятся к понятию угла между пересекающимися прямыми.
Слайд 9A
C
D1
A1
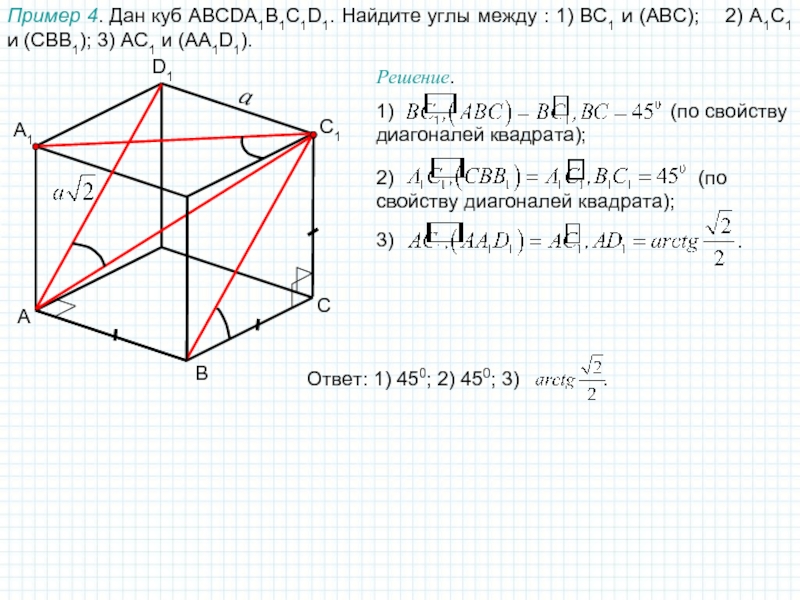
Пример 4. Дан куб ABCDA1B1C1D1. Найдите углы между : 1)
BC1 и (АBC); 2) A1C1 и (CBB1); 3) AC1
и (AA1D1).B
C1
a
Теги
