Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дельтоид 9 класс
Содержание
- 1. Дельтоид 9 класс
- 2. Цель: изучить четырехугольник «Дельтоид», описать его свойства
- 3. Основные понятия Дельтоид
- 4. Виды дельтоидов Существуют два вида
- 5. Свойство 1. Углы дельтоида между
- 6. Рассмотрим треугольники АВС и АDC. У них
- 7. Свойство 2. Главная диагональ дельтоида
- 8. Из доказательства свойства1 следует, что ∆ АВС
- 9. Свойство 3. Диагонали дельтоида (или
- 10. Рассмотрим ∆ АВС. Он является
- 11. Свойство 4. В любой выпуклый дельтоид можно вписать окружность.Дано: АВСD — дельтоид.Вписать:окружность (О; r).
- 12. Доказательство свойства 4.Известно, что если суммы длин
- 13. Свойство 5. Средние линии дельтоида
- 14. Доказательство свойства 5.MF║BD и LE ║DB, т.е.
- 15. Свойство 6. Площадь дельтоида определяется по формуле:
- 16. Доказательство свойства 6.Рассмотрим ∆ АDC, он равнобедренный,
- 17. Свойство 7Периметр дельтоида определяется по формулеР =
- 18. Свойство 8 Не главная диагональ делит
- 19. Признак 1. Если у четырехугольника только
- 20. Признак 2. Если в
- 21. Доказательство признака 2.Дано: четырехугольник АВСD, d1 ┴
- 22. Доказательство признака 2.5. Биссектриса равнобедренного треугольника, проведенная
- 23. Признак 3. Если в четырехугольнике одна
- 24. Доказательство признака 3.Дано : четырехугольник АВСD, d1
- 25. Задача 1 Найдите периметр дельтоида ABCD,
- 26. Задача 2 В параллелограмме АВСD диагональ
- 27. Задача 3 Дано: АВСD – параллелограмм;АС
- 28. Решение задачи 2.
- 29. История изучения дельтоидаДельтоида (кривая Штейнера) — плоская
- 30. Дельтоид в окружающем нас мире.
- 31. Дельтоидом называют мышцы плечаЧеловеческий мозжечок имеет рисунок,
- 32. Тест « Знаешь ли ты дельтоид?»Вопрос 1Выберите
- 33. Тест « Знаешь ли ты дельтоид?»Вопрос 2.
- 34. Тест « Знаешь ли ты дельтоид?»Вопрос 3.Выбери четырехугольник, который может быть выпуклым:ТрапецияРомбДельтоидКвадрат
- 35. Тест « Знаешь ли ты дельтоид?»Вопрос 4.Как
- 36. Тест « Знаешь ли ты дельтоид?»Вопрос 5.АВСD
- 37. Тест « Знаешь ли ты дельтоид?»Вопрос 6.Выбери
- 38. Тест « Знаешь ли ты дельтоид?»Вопрос 7.Выберите
- 39. Тест « Знаешь ли ты дельтоид?»Вопрос 8.Какого
- 40. Спасибо за внимание
- 41. Скачать презентанцию
Цель: изучить четырехугольник «Дельтоид», описать его свойства и признаки, составить учебное пособие.Задачи:Изучить и проанализировать литературу по данной теме.Сформулировать и доказать свойства и признаки дельтоида.Составить и решить задачи о дельтоиде.Продемонстрировать наличие дельтоидов
Слайды и текст этой презентации
Слайд 1Дельтоид
Выполнили: обучающиеся
8 «А» класса ГБОУ
школы-интерната №113
г.о. Самара
Елдышева Дарья,
Левчук Станислав,
Шапкина Алина
Руководитель:
Губарева Е.Г.
Слайд 2Цель: изучить четырехугольник «Дельтоид», описать его свойства и признаки, составить
учебное пособие.
Задачи:
Изучить и проанализировать литературу по данной теме.
Сформулировать и доказать
свойства и признаки дельтоида.Составить и решить задачи о дельтоиде.
Продемонстрировать наличие дельтоидов в окружающем нас мире.
Составить тест проверки знаний о дельтоидах.
Слайд 3Основные понятия
Дельтоид — четырехугольник, у
которого есть две пары смежных сторон. Равными являются две пары
смежных сторон. Дельтоид имеет форму, похожую на воздушного змея.
Слайд 4Виды дельтоидов
Существуют два вида дельтоидов: выпуклый и
невыпуклый. Все углы выпуклого дельтоида меньше развернутого угла, а один
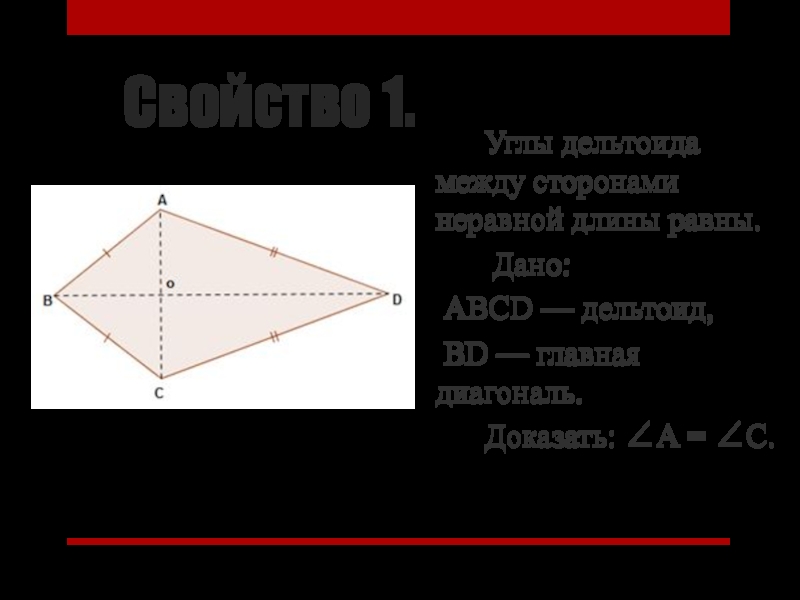
из углов невыпуклого больше развернутого.
Слайд 5Свойство 1.
Углы дельтоида между сторонами неравной длины
равны.
Дано:
АВСD — дельтоид,
ВD —
главная диагональ.Доказать: ∠А = ∠С.
Слайд 6Рассмотрим треугольники АВС и АDC. У них сторона АС –
общая. Стороны АВ = АD,
ВС = СD по условию.
Значит, треугольники равны по третьему признаку равенства треугольников. Следовательно ﮮАВС = ﮮАDС. Что и требовалось доказать.Доказательство свойства 1.
Слайд 7Свойство 2.
Главная диагональ дельтоида является биссектрисой противолежащих
углов.
Дано: АВСD - дельтоид,
BD — главная диагональ.Доказать: BD - биссектриса.
Слайд 8Из доказательства свойства1 следует, что
∆ АВС = ∆ АDС.
Значит ﮮВАС = ﮮDАС,
ﮮВСА = ﮮDСА. Вывод: АС – биссектриса,
что и требовалось доказать.Доказательство свойства 2.
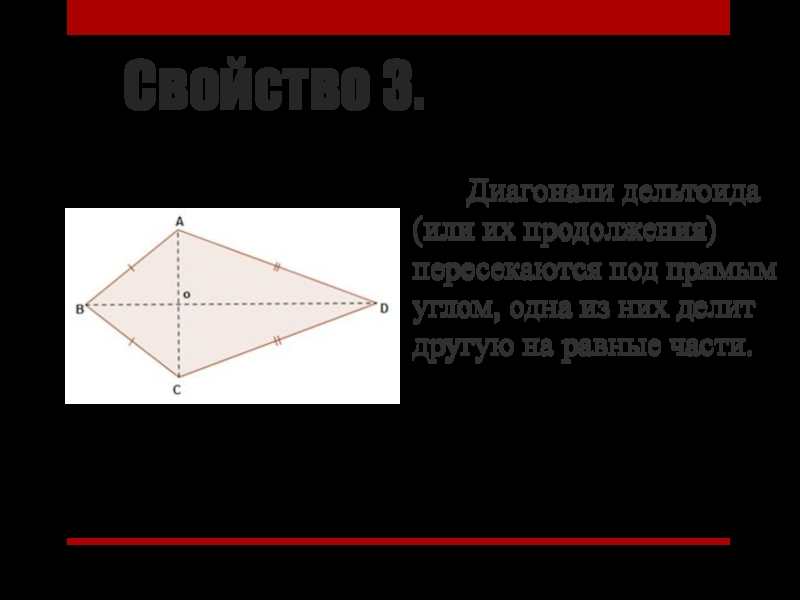
Слайд 9Свойство 3.
Диагонали дельтоида (или их продолжения) пересекаются
под прямым углом, одна из них делит другую на равные
части.
Слайд 10 Рассмотрим ∆ АВС. Он является равнобедренным по условию.
Из этого следует, что биссектриса ﮮВ, проведенная к основанию треугольника,
является еще высотой и медианой. Следовательно,ОА = ОС, а диагонали ВD ┴ АС одна из них делится точкой пересечения пополам.
Что и требовалось доказать.
Доказательство свойства 3.
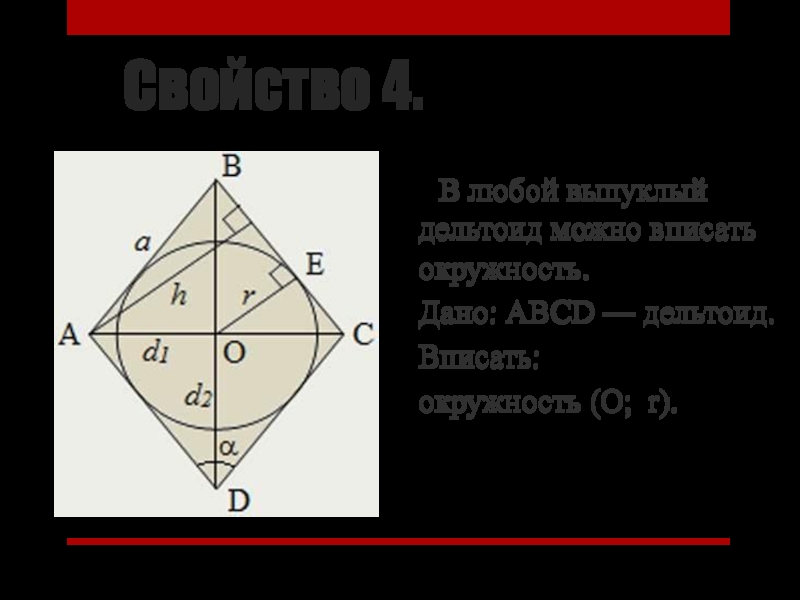
Слайд 11Свойство 4.
В любой выпуклый дельтоид можно вписать окружность.
Дано:
АВСD — дельтоид.
Вписать:
окружность (О; r).
Слайд 12Доказательство свойства 4.
Известно, что если суммы длин противоположных сторон выпуклого
четырехугольника равны, то в него можно вписать окружность (т.к. АВ
= СВ и АD = DС, то АВ + DС = СВ + АD).По определению дельтоида, это выпуклый четырехугольник, у которого есть только две пары смежных сторон. Значит АВ +DС = АD + ВС.
Точка О пересечение биссектрис СО и АО углов С и А. Следовательно: в дельтоид можно вписать окружность и притом только одну.
Что и требовалось доказать.
Слайд 13Свойство 5.
Средние линии дельтоида образуют прямоугольник, периметр
которого равен сумме диагоналей данного дельтоида.
Дано: АВСD — дельтоид,
L, E, F, M - середины сторон.Доказать: MLEF - прямоугольник.
Слайд 14Доказательство свойства 5.
MF║BD и LE ║DB, т.е. MF ║LE
ML ║CA
и EF ║CA, т.е. ML ║ EF
CA ┴ BD, значит
и ML и EF ┴ MF и LE, отсюда следует, что ﮮМ = ﮮL, ﮮЕ = ﮮF, и ML + EF = CA и MF + LE = BD.Следует, что периметр = ML + EF + MF +LE = = CA + BD.
Что и требовалось доказать.
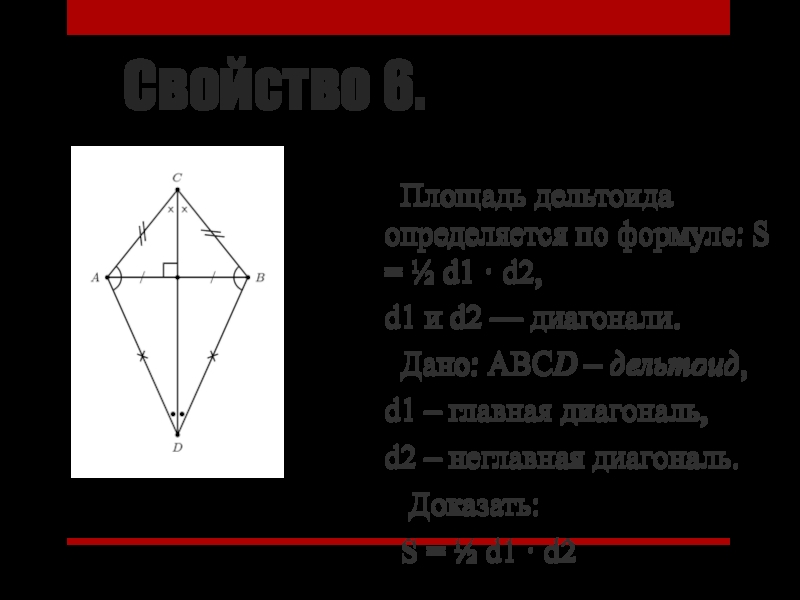
Слайд 15Свойство 6.
Площадь дельтоида определяется по формуле: S = ½
d1 · d2,
d1 и d2 — диагонали.
Дано: АВСD –
дельтоид,d1 – главная диагональ,
d2 – неглавная диагональ.
Доказать:
S = ½ d1 · d2
Слайд 16Доказательство свойства 6.
Рассмотрим ∆ АDC, он равнобедренный, ОD – высота.
Площадь равна высоте умноженной на половину основания. S (ADC) =
0,5∙ DO∙ d2.Рассмотрим ∆ BCA - равнобедренный, ОB - высота. S (BCA) = 0,5∙ BO∙ d2.
S (ABCD) = S (ADC) + S (BCA) = 0,5∙ DO∙ d2 + +0,5∙ BO∙ d2 = 0,5∙d1∙d2.
Что и требовалось доказать.
Слайд 17Свойство 7
Периметр дельтоида определяется по формуле
Р = 2·(а + b),
где
a и b — смежные неравные стороны дельтоида.
(принимаем без доказательства)
Слайд 18Свойство 8
Не главная диагональ делит дельтоид на два
равнобедренных треугольника.
Дано: АВСD -дельтоид.
Доказательство: по определению дельтоида очевидно,
что ∆ АВD и ∆ВСD равнобедренные.
Слайд 19Признак 1.
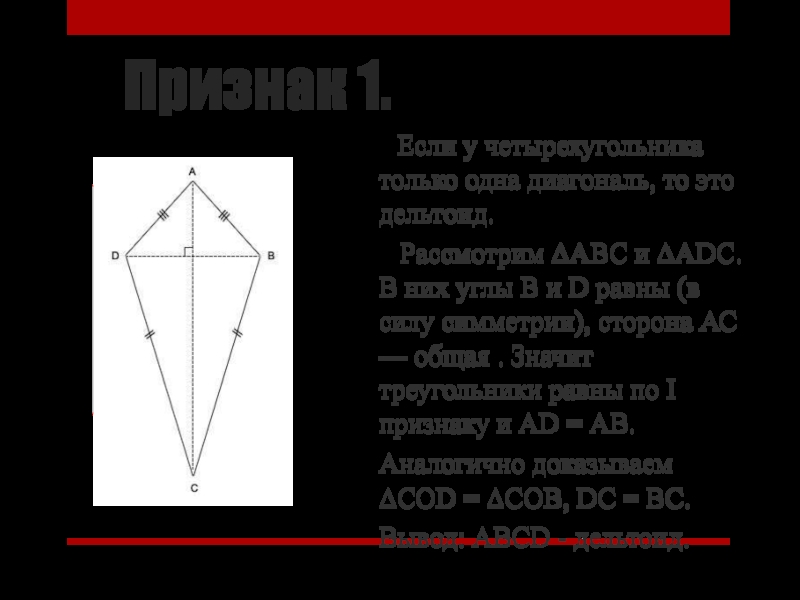
Если у четырехугольника только одна диагональ, то
это дельтоид.
Рассмотрим ΔАВС и ΔАDС. В них углы
В и D равны (в силу симметрии), сторона АС — общая . Значит треугольники равны по I признаку и АD = АВ.Аналогично доказываем ΔСОD = ΔСОВ, DС = ВС.
Вывод: АВСD - дельтоид.
Слайд 20Признак 2.
Если в четырехугольнике только одна
из диагоналей точкой пересечения делится пополам и перпендикулярна ей, то
этот четырехугольник - дельтоид.
Слайд 21Доказательство признака 2.
Дано: четырехугольник АВСD, d1 ┴ d2, AO =
OC.
Доказать: АВСD – дельтоид.
Док-во: 1. Рассмотрим ∆ АОD, АВ входит
в ∆ АОВ и АО ┴ DВ.2. Рассмотрим ∆ АОD и ∆ АОВ: АО – общая, ﮮ1 = ﮮ2
∆ АОD = ∆ АОВ, по катету и противолежащему углу, отсюда АD = АВ.
3. DС входит в ∆ СОD и СО ┴ DВ.
4. Рассмотрим ∆ СОD и ∆ СОВ: ОС – общая, ﮮ3 = ﮮ4
∆ СОD = ∆ СОВ, по катету и прилежащему острому углу, отсюда DС = ВС.
Слайд 22Доказательство признака 2.
5. Биссектриса равнобедренного треугольника, проведенная из вершины равнобедренного
треугольника, является медианой и высотой, т.е. АО и СО –
медианы, значит DO = OB.6. DO – перпендикуляр, не является медианой, т.к. ∆ ADC не равнобедренный. Значит ABDC – дельтоид по определению.
Что и требовалось доказать.
Слайд 23Признак 3.
Если в четырехугольнике одна из двух, взаимно
перпендикулярных диагоналей является биссектрисой, не равных противоположных углов, а другая
не является биссектрисой другой пары углов, то этот четырехугольник – дельтоид.
Слайд 24Доказательство признака 3.
Дано : четырехугольник АВСD, d1 –биссектриса (ﮮ,1 =
2), ﮮ d2 – не является биссектрисой, d1 ┴ d2.
Доказать:
АВСD – дельтоид.Док-ть: АВ входит в ∆ АОВ и АО ┴ DВ.
2. Рассмотрим ∆ АОD и ∆ АОВ: АО – общая. ﮮ 1 = ﮮ2. т.к. d1 –биссектриса по условию,
∆ АОD = ∆ АОВ, по катету и противолежащему углу, отсюда АD = АВ.
3. DС входит в ∆ СОD и СО ┴ DВ.
Слайд 25Задача 1
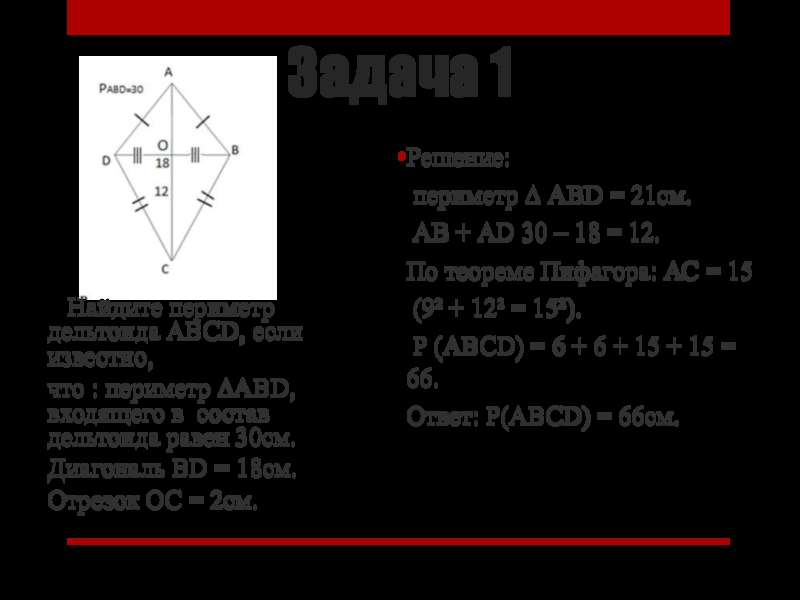
Найдите периметр дельтоида ABCD, если известно,
что :
периметр ∆ABD, входящего в состав дельтоида равен 30см.
Диагональ BD =
18см.Отрезок ОС = 2см.
Решение:
периметр ∆ ABD = 21см.
АВ + АD 30 – 18 = 12.
По теореме Пифагора: АС = 15
(9² + 12² = 15²).
Р (АВСD) = 6 + 6 + 15 + 15 = 66.
Ответ: Р(АВСD) = 66см.
Слайд 26Задача 2
В параллелограмме АВСD диагональ АС вдвое больше
стороны АВ. На стороне ВС выбрана точка К так, что
∆
АDВ = ∆ КDВ.В каком отношении точка К делит сторону ВС?
Слайд 27Задача 3
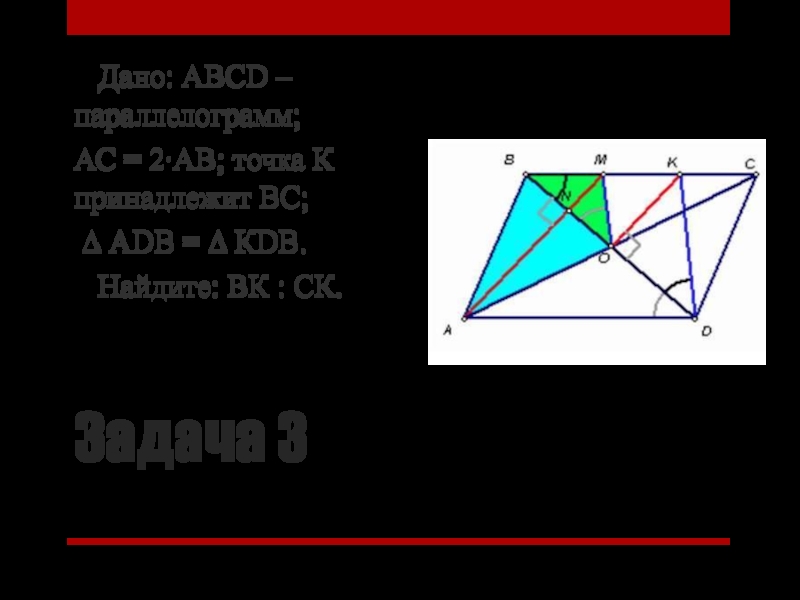
Дано: АВСD – параллелограмм;
АС = 2∙АВ; точка
К принадлежит ВС;
∆ АDВ = ∆ КDВ.
Найдите:
ВК : СК.
Слайд 29История изучения дельтоида
Дельтоида (кривая Штейнера) — плоская алгебраическая кривая, описываемая
фиксированной точкой окружности, катящейся по внутренней стороне другой окружности, радиус
которой в 3 раза больше радиуса первой.
Слайд 31Дельтоидом называют мышцы плеча
Человеческий мозжечок имеет рисунок, который ученые называют
(деревом жизни), составной частью которого являются дельтоиды.
Слайд 32Тест « Знаешь ли ты дельтоид?»
Вопрос 1
Выберите верное утверждение.
Если в
четырехугольнике главная диагональ – биссектриса противоположных углов, то это дельтоид;
Если
в четырехугольнике две стороны равны, то это дельтоид;Если в четырехугольнике есть пара смежных сторон, то это дельтоид;
Если четырехугольник образован двумя равнобедренными треугольниками, то это дельтоид.
Слайд 33Тест « Знаешь ли ты дельтоид?»
Вопрос 2.
В дельтоиде смежные
стороны относятся как 2 : 3. Найдите меньшую сторону, если
периметр дельтоида равен 60 см.6
12
9
10.
Слайд 34Тест « Знаешь ли ты дельтоид?»
Вопрос 3.
Выбери четырехугольник, который может
быть выпуклым:
Трапеция
Ромб
Дельтоид
Квадрат
Слайд 35Тест « Знаешь ли ты дельтоид?»
Вопрос 4.
Как называется четырехугольник, у
которого только одна диагональ является биссектрисой противолежащих углов?
Трапеция
Дельтоид
Ромб
Прямоугольник
Слайд 36Тест « Знаешь ли ты дельтоид?»
Вопрос 5.
АВСD – дельтоид. Площадь
∆АВС = 45. Площадь ∆ АСD = 55. ∆АВС равносторонний,
∆АСD – равнобедренный. Найдите площадь дельтоида,60
50
55
100
Слайд 37Тест « Знаешь ли ты дельтоид?»
Вопрос 6.
Выбери верные утверждения:
Средняя линия
дельтоида – это линия, соединяющая стороны дельтоида;
Главная диагональ дельтоида –
это диагональ, соединяющая вершины неравных углов дельтоида;Дельтоид – четырехугольник, в котором две пары смежных сторон равны;
Неглавной диагональю дельтоида называется диагональ, соединяющая две его вершины.
Слайд 38Тест « Знаешь ли ты дельтоид?»
Вопрос 7.
Выберите определение дельтоида:
Дельтоид –
это четырехугольник, у которого стороны попарно равны;
Дельтоид – это четырехугольник,
у которого смежные стороны попарно равны;Дельтоид – это четырехугольник, у которого у которого диагонали взаимно перпендикулярны;
Дельтоид – это четырехугольник, у которого две стороны равны и параллельны;
Слайд 39Тест « Знаешь ли ты дельтоид?»
Вопрос 8.
Какого из перечисленных элементов
нет у дельтоида?
угол;
Диагональ;
Радиус вписанной окружности;
Радиус описанной окружности.
