Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
2_11.ppt
Содержание
- 1. 2_11.ppt
- 2. Основная идея дискретных алгоритмовОсновная идея – преобразование
- 3. Разбиение Сузуки – Троттера для модели ХаббардаМодель
- 4. Разбиение Сузуки – Троттера для модели ХаббардаВыберем
- 5. Представление шахматной доскиПо горизонтальной оси отложены номера
- 6. Учет спина частицДва варианта учета спина частиц:
- 7. Алгоритм Монте-КарлоНеобходимо перебрать все возможные состояния системы,
- 8. Алгоритм Монте-КарлоВсе процедуры для обновления мгновенных конфигураций
- 9. Расчет средних. Величины, сохраняющие число частицСхема Метрополиса:Величины, локально сохраняющие число частиц:Для оператора энергии:
- 10. Расчет средних. Величины, не сохраняющие число частицВводится
- 11. Расчет средних. Функция ГринаНеобходимы два дополнительных временных
- 12. Скачать презентанцию
Основная идея дискретных алгоритмовОсновная идея – преобразование квантовой d-мерной задачи к (d+1)-мерной классической путем введения «временных» разрезов в пространстве мнимого времени 0
Слайды и текст этой презентации
Слайд 2Основная идея дискретных алгоритмов
Основная идея – преобразование квантовой d-мерной задачи
к (d+1)-мерной классической путем введения «временных» разрезов в пространстве мнимого
времени 0<τ<β=1/TРазбиение Сузуки – Троттера:
верно с точностью (Δτ)2. Δτ= β/M, M≫1
Статистическая сумма представляется в виде произведения операторов эволюции
Разбиение Сузуки – Троттера позволяет представить квантовую задачу как некоторую классическую, эволюционирующую по шкале мнимого времени как по дополнительной классической переменной
Слайд 3Разбиение Сузуки – Троттера
для модели Хаббарда
Модель Хаббарда:
Разбиение для статистической суммы:
Разобьем
гамильтониан на два типа связей (например, четные и нечетные):
Если
– полный набор состояний, относящийся к временному срезу , то
Слайд 4Разбиение Сузуки – Троттера для модели Хаббарда
Выберем состояния
в представлении чисел заполнения. Тогда в этом полном
наборе состояний оператор будет диагонален, и поэтому надо определить лишь матричные элементы оператора кинетической энергии, которые оказываются произведением множителей простого вида:Фактически для модели Хаббарда задача сводится к расчету матричных элементов двухузельной задачи, которые рассчитываются аналитически:
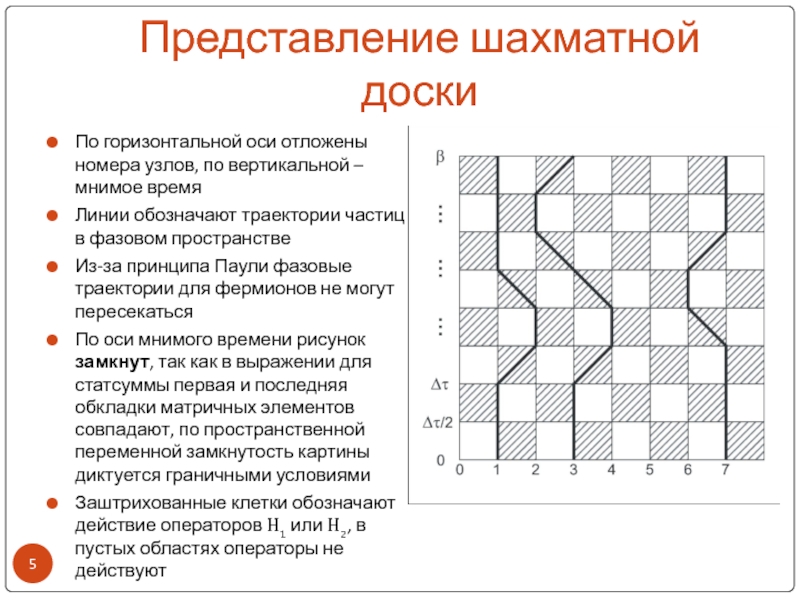
Слайд 5Представление шахматной доски
По горизонтальной оси отложены номера узлов, по вертикальной
– мнимое время
Линии обозначают траектории частиц в фазовом пространстве
Из-за принципа
Паули фазовые траектории для фермионов не могут пересекатьсяПо оси мнимого времени рисунок замкнут, так как в выражении для статсуммы первая и последняя обкладки матричных элементов совпадают, по пространственной переменной замкнутость картины диктуется граничными условиями
Заштрихованные клетки обозначают действие операторов H1 или H2, в пустых областях операторы не действуют
Слайд 6Учет спина частиц
Два варианта учета спина частиц: две шахматные доски
или два сорта траекторий на одной доске
На каждом узле теперь
может быть четыре состояния:
Слайд 7Алгоритм Монте-Карло
Необходимо перебрать все возможные состояния системы, т.е. все возможные
диаграммы
Перебор конфигураций происходит за счет их преобразования – из одной
конфигурации получается некоторая другая, отличающаяся от исходной определенным образомПеребираются не все возможные конфигурации, а преимущественно те, которые дают основной вклад в статсумму
В простейшем варианте траекторного алгоритма МК в дискретном времени для преобразования системы мировых линий используются две пары процессов
Слайд 8Алгоритм Монте-Карло
Все процедуры для обновления мгновенных конфигураций разбиваются попарно на
«прямые» и «обратные»
Каждая пара процедур удовлетворяет уравнению детального баланса:
Схема Метрополиса:
Слайд 9Расчет средних.
Величины, сохраняющие число частиц
Схема Метрополиса:
Величины, локально сохраняющие число частиц:
Для
оператора энергии:
Слайд 10Расчет средних.
Величины, не сохраняющие число частиц
Вводится дополнительный временной разрез, на
котором допустимы разрывы траекторий
Необходимо реализовать независимые МК-процедуры для числителя и
знаменателяВся полезная информация снимается только с одного временного разреза
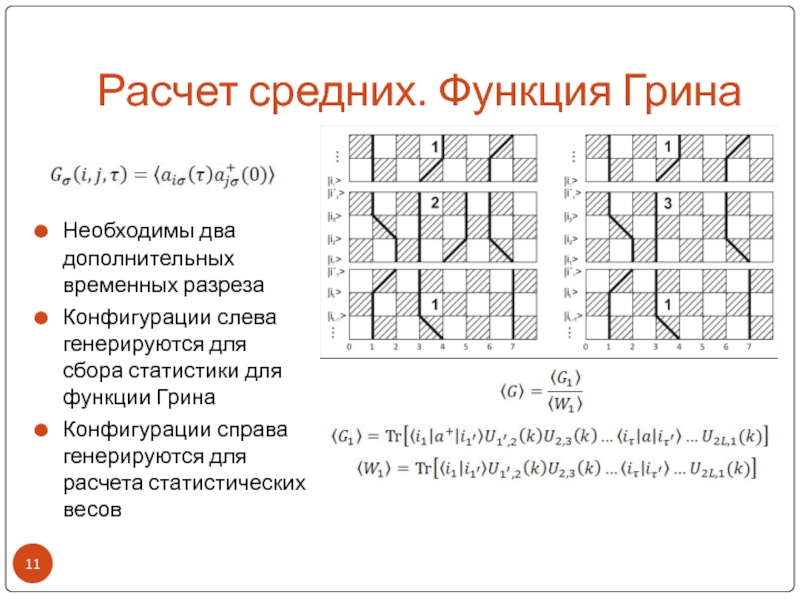
Слайд 11Расчет средних. Функция Грина
Необходимы два дополнительных временных разреза
Конфигурации слева генерируются
для сбора статистики для функции Грина
Конфигурации справа генерируются для расчета
статистических весов