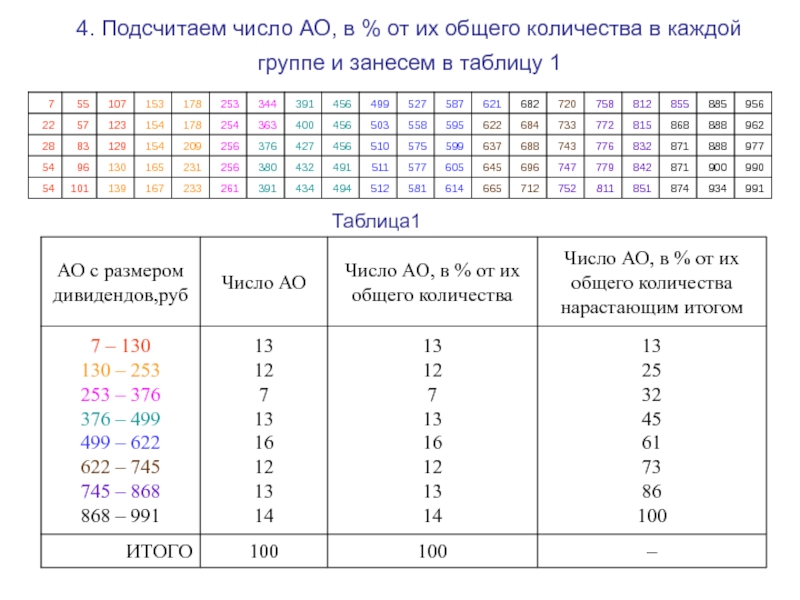
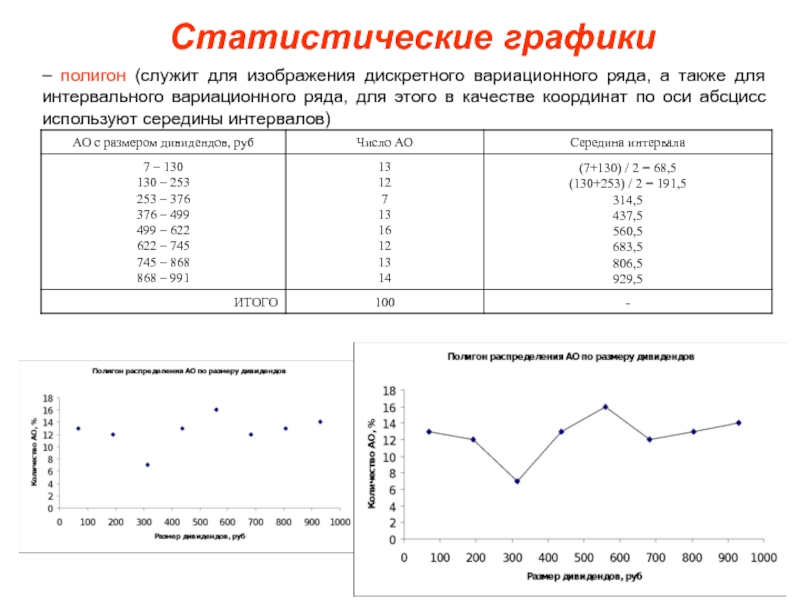
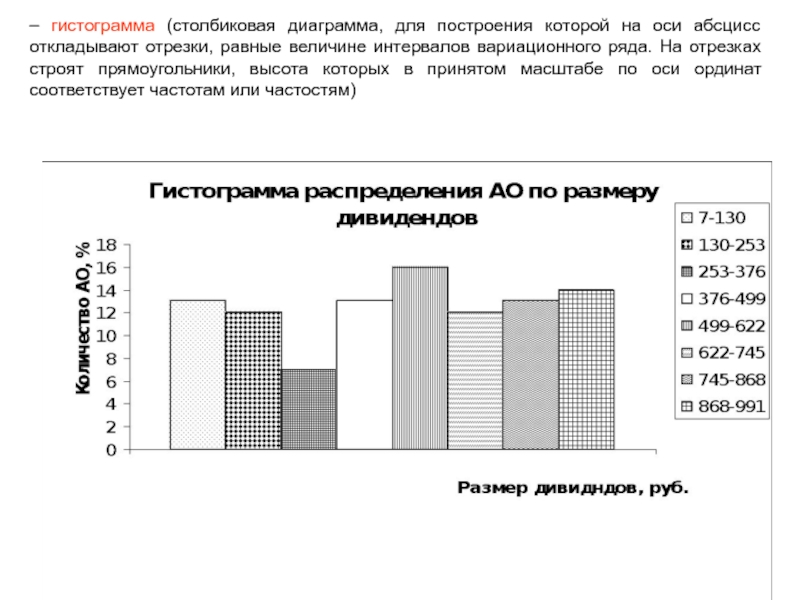
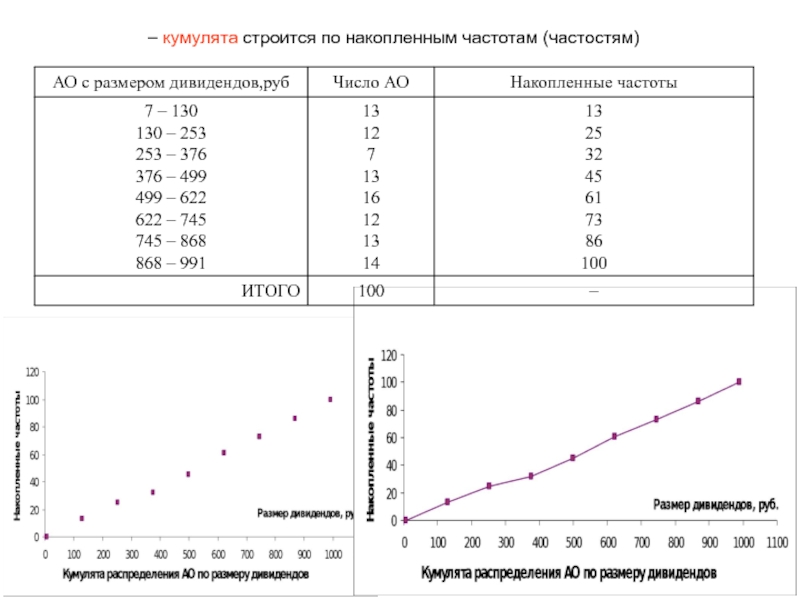
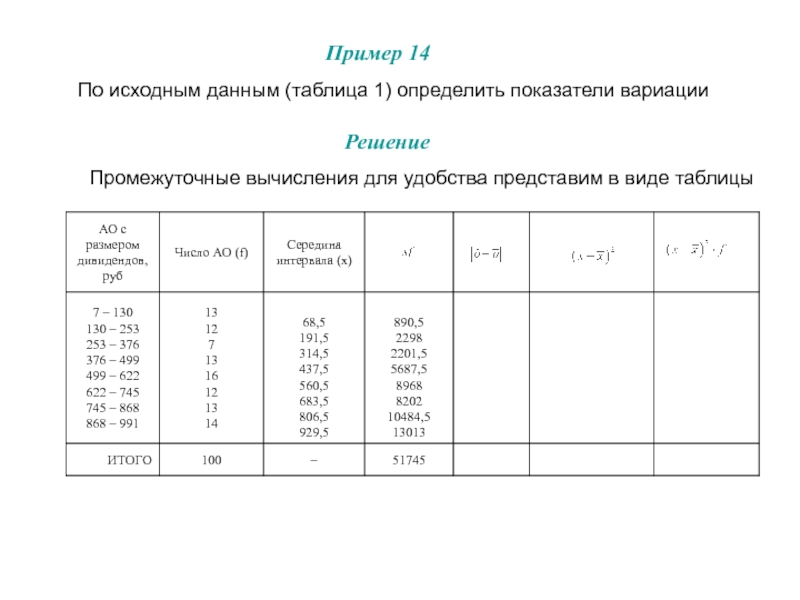
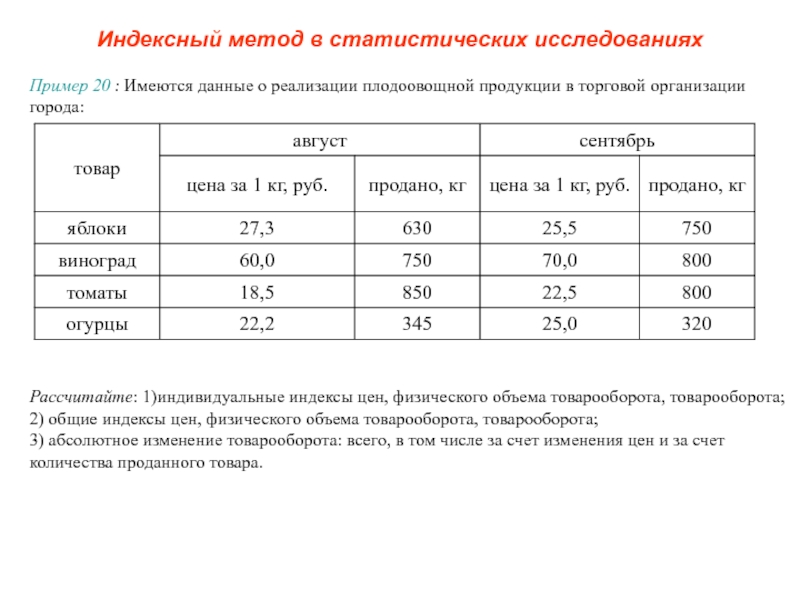
с равными интервалами, если известны следующие данные о размере дивидендов
в рублях: 107, 499, 581, 101, 614, 54, 376, 123, 511, 130, 154, 22, 231, 595, 83, 54, 622, 456, 7, 456, 527, 344, 55, 811, 57, 400, 165, 209, 380, 178, 28, 684, 391, 154, 167, 605, 812, 900, 139, 363, 752, 129, 688, 253, 256, 96,153, 261, 758, 494, 233, 977, 178, 391, 491, 256, 432, 779, 254, 577, 868, 434, 747, 456, 842, 720, 696, 427, 888, 851, 599, 956, 510, 772, 621, 575, 991, 503, 645, 512, 832, 733, 871, 712, 776, 990, 558, 888, 871, 934, 743, 962, 682, 874, 885, 665, 855, 587, 815, 637.Пример 1
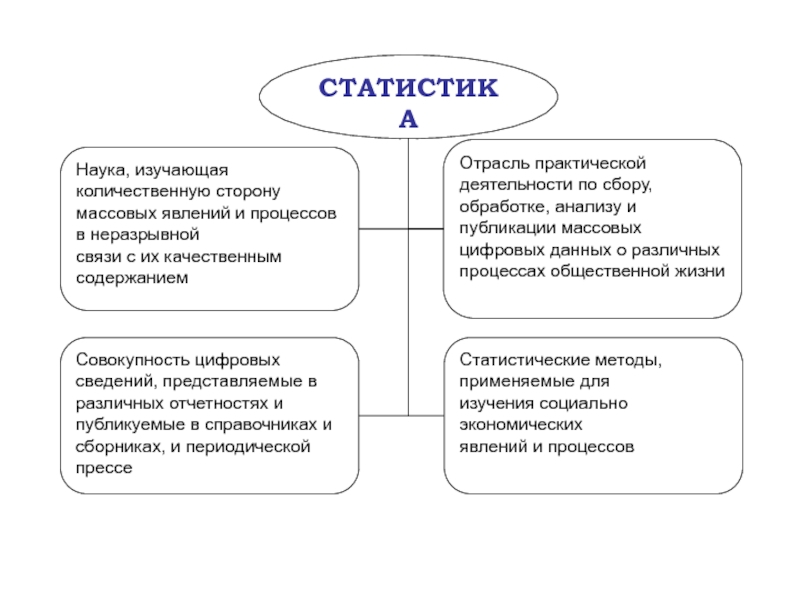
Сводки и группировка данных