Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Реляционное исчисление
Содержание
- 1. Реляционное исчисление
- 2. СОДЕРЖАНИЕРеляционные исчисленияИсчисление КоддаЯзык ALPHA Эквивалентность и полнотаПримеры
- 3. Теория множеств и логикаТеория множеств
- 4. Реляционное исчислениеПодмножество формул исчисление предикатовФормальное описание того,
- 5. Кортежное реляционное исчисление (TRC)Запрос ( в простейшем
- 6. TRC - Базовые составляющие языкаКонстанты: 7, 'john',
- 7. TRC - Правильно определенные формулы Атомарные формулы:
- 8. TRC - Свободные и связанные переменные. Запросы.Говорят,
- 9. Пример БД для запросов в РИFAC FACULTY
- 10. TRC - Примеры проекции, селекции и соединения1)
- 11. TRC - Примеры кванторов существованияЗапрос. Вывести имена
- 12. TRC - Примеры кванторов общностиЗапрос. Вывести номера
- 13. TRC - Безопасные формулы (запросы)Можно формулировать запросы,
- 14. TRC - Ограниченные переменныеКортежная переменная ограничена, если
- 15. Ограниченные логические связки Если две формулы F
- 16. Ограниченные кванторыПримеры: ∃x(x.Fund < 5) – квантор существования
- 17. Доменное реляционное исчисление (DRC)Запрос имеет вид
- 18. Примеры запросов в DRC1) ПроекцияЗапрос. Вывести названия
- 19. Эквивалентность RA, TRC, DRC и реляционная
- 20. Реляционное исчисление Кодда (СRС)Является подмножеством исчисления предикатов
- 21. CRC – основные составляющие Константы: 7, 'john',
- 22. CRC - правильно определенные формулыТермы: P.t –
- 23. Формула, правильно определенная на кванторах По
- 24. Формула с областью определения Формула W называется
- 25. Альфа-выраженияВыражение (t1, t2,…, tk) : W называется
- 26. Язык ALPHA Упрощенный синтаксис: RANGE [
- 27. Примеры запросов в ALPHA и CRCЗапрос. Вывести
- 28. ЗаключениеРеляционное исчисление является декларативным (не процедурным)
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 7. Реляционное исчисление
Национальный авиационный университет
Факультет компьютерных наук
Кафедра инженерии программного
обеспечения
Слайд 3Теория множеств и логика
Теория множеств Исчисление предикатов
Связь
(отношений)
Множество М
Р(х); Р – предикатный символ х ∈ М ⇔ Р(х) = t
х – переменнаяМ θ N Р(х) θ Q(y) х ∈ М θ N ⇔ Р(х) θ Q(y) = t θ = {∪, ∩, , −} θ = {∨, ∧, ¬, →}
Теория множеств
Исчисление предикатов
Реляционная алгебра
Реляционное исчисление
Пример связи ТМ и ИП:
Слайд 4Реляционное исчисление
Подмножество формул исчисление предикатов
Формальное описание того, ЧТО следует получить
из базы
данных. Например:
ЕЯ - "Выдать факультеты с фондом финансирования
> 10000"РИ - {t | (FAC(t) & t.fund > 10000}
Имеет средства языка запросов, но не обладает возможностями манипулирования данными (как и реляционная алгебра)
Два варианта реляционного исчисления:
Кортежное реляционное исчисление (TRC) – переменные представляют строки отношений
Доменное реляционное исчисление (DRC) - переменные представляют домены атрибутов отношений
Слайд 5Кортежное реляционное исчисление (TRC)
Запрос ( в простейшем случае) имеет вид
{t | (F(t)}
t - кортежная переменная;
F(t) - формула, в которой
присутствует кортежная переменная tОтвет: Множество всех таких кортежей t, для которых формула F(t) принимает значение true.
Формула: Рекурсивно определяется через атомарные формулы и построением более сложных формул с помощью логических связок и кванторов.
SQL: Является формальной основной языка SQL.
Слайд 6TRC - Базовые составляющие языка
Константы: 7, 'john', 3.14159 и т.д.
Кортежные
переменные: t1, t2,... –
интерпретируются кортежами отношений.
Срезы кортежных переменных: t.a,…
а - имя атрибута, значение которого входит в
состав кортежа. Предикатные символы: P, P1,...,Q, Q1,… Интерпретируются отношениями
Операторы (предикаты) сравнения : = {=, <, <=, >, >=, <>} и т.д.
Логические связки: ∨ (или), ∧(&) (и), ¬ (не ), → (влечет)
Кванторы: ∃(существует), ∀(для любого)
Слайд 7TRC - Правильно определенные формулы
Атомарные формулы:
P(t) - P
- предикатный символ, - t - кортежная переменная.
Если Р интерпретируется отношением R, то P(t) означает t ∈ Rt.a θ t.b - t.a и t.b - срезы
t.a θ с - t.a - срез, с - константа
Правильно построенные формулы (ппф):
Атомарные формулы являются ппф;
Если F ппф, то ппф также являются ¬F и (F)
Если F и G ппф, то ппф также являются F ∨ G, F ∧ G, F → G
Если F ппф со свободной переменной t, то ппф также являются ∃tF(t) и ∀tF(t).
Слайд 8TRC - Свободные и связанные переменные. Запросы.
Говорят, что наличие кванторов
∃tF(t) и ∀tF(t). связывает переменную t в формуле F. Переменная,
которая не связана, называется свободной.Запрос - в общем случае это выражение вида:
{(t1,t2,...) | (F(t1,t2,...)}
где - t1,t2,... - кортежные переменные или их срезы;
- F(t1,t2,...) - формула, в которой присутствуют свободные
кортежные переменные t1,t2,...
ВНИМАНИЕ: Переменные t1,t2,..., расположенные слева от символа ’|’, должны быть единственными свободными переменными в формуле F. Это значит, что если F содержит другие переменные, то они должны быть связанными с помощью кванторов.
Слайд 9Пример БД для запросов в РИ
FAC FACULTY (FNo, Name, Dean,
Bld, Fund)
DEP DEPARTMENT (DNo, FNo, Name, Head, Bld, Fund)
TCH TEACHER(TNo,
DNo, Name, Post, Tel, Salary, Comm)
GRP GROUP(GNo, DNo, Course, Num, Quantity, CurNo)
SBJ SUBJECT(SNo, Name)
ROM ROOM (RNo, Num, Building, Seats)
LEC LECTURE (TNo, GNo, SNo, RNo, Type, Day, Week)
Предикатные символы
Отношения БД
Слайд 10TRC - Примеры проекции, селекции и соединения
1) Проекция
Запрос.
Вывести названия факультетов и имена их деканов
2) Селекция и проекция
Запрос. Вывести имена и должности преподавателей, имеющих зарплату > 1000 и надбавку > 500{(f.Name, f.Dean)|FAC(f)}
3) Соединение, селекция и проекция
Запрос. Вывести имена факультетов и их кафедр,
расположенных (факультетов) в корпусе 5
{(t.Name, t.Post) | TCH(t) & t.Salary > 1000 & t.Comm > 500}
{(f.Name,d.Name) | FAC(f) & DEP(d) & f.FNo = d.FNo & f.Bld = 5}
Слайд 11
TRC - Примеры кванторов существования
Запрос. Вывести имена факультетов корпуса 5
и их кафедр
{(f.Name,d.Name) | DEP(d) & FAC(f) & f.FNo =
d.FNo & f.Bld = 5}Запрос. Вывести имена кафедр факультетов корпуса 5
{d.Name | DEP(d) & ∃f(FAC(f) & f.FNo = d.FNo & f.Buld = 5)}
Запрос. Вывести имена преподавателей-профессоров, имеющих
лекции в группах первого курса
{t.Name | TCH(t) & t.Post='professor' &
∃l(LEC(l) & l.TNo = t.Tno &
∃g(GRP(g) & l.GNo = g.GNo & g.Course = 1))}
Вывести имена профессоров,
для которых существуют такие лекции,
для которых (лекций) существуют группы первого курса
Слайд 12TRC - Примеры кванторов общности
Запрос. Вывести номера преподавателей, читающих лекции
во всех группах
{l.TNo | LEC(l) & ∀g(GRP(g) → g.GNo =
l.GNo)}Запрос. Вывести номера преподавателей, которые читают лекции во всех группах первого курса
{l.TNo | LEC(l) & ∀g((GRP(g) & g.Course = 1) → g.GNo = l.GNo)}
Запрос. Вывести имена преподавателей, которые читают лекции во всех группах первого курса
{t.Name | TCH(t) & ∃l(LEC(l) & l.TNo = t.TNo &
∀g((GRP(g) & g.Course = 1) → g.GNo = l.GNo)}
Вывести имена преподавателей,
для которых существуют такие лекции,
которые читаются всем группам 1 курса
Слайд 13TRC - Безопасные формулы (запросы)
Можно формулировать запросы, содержащие ппф, но
не имеющие интерпретации в БД. Или, другими словами, имеющие бесконечное
к-во ответов (дающие в результате бесконечные отношения). Примеры:Запрос называется безопасным, если он интерпретируется конечным отношением.
Для построения безопасных запросов:
все переменные в формуле должны быть ограниченными;
все логические связки должны быть ограниченными;
все кванторы должны быть ограниченными.
{t | t.Post = 'professor'}
{t | ¬TCH(t)}
{(t,d) | TCH(t) ∨ DEP(d)}
Слайд 14TRC - Ограниченные переменные
Кортежная переменная ограничена, если она принадлежит предикату,
который интерпретируется отношением БД, или если она ограничена другой переменной
или константой.Переменная t ограниченна, если:
она появляется в предикате Р(t), где Р интерпретируется отношением БД;
она появляется в формуле t.a1 = c1 & ... & t.an = cn, где
a1,..., an - все атрибуты корежа t, а c1, ..., cn - константы;
она появляется в формуле t = s, где s – ограниченная переменная.
Примеры:
P(t) - переменная t ограничена предикатом P
P(t) & t = x - переменная x ограничена ограниченной переменной t
t.Name=‘john’ & t.Post=‘prof’ & t.Salary = ‘1200’
Слайд 15Ограниченные логические связки
Если две формулы F и G имеют
ограниченные переменные, то:
F ∨ G будет являться формулой с ограниченными
переменными, если F и G имеют одинаковые свободные переменные;F & G всегда является формулой с ограниченными переменной не зависимо от того, совпадают ли в этих формулах переменные;
F & ¬G является формулой с ограниченной переменной, если в этих формулах совпадают свободные переменные;
F → G никогда не является формулой с ограниченной переменной.
Примеры:
P(t) ∨ Q(t) – формула с ограниченной переменной
P(t) ∨ Q(q) – переменные в результирующей формуле не ограничены
P(t) & Q(q) – формула с ограниченной переменной
¬Q(t) – не является формулой с ограниченной переменной
P(t) & ¬Q(q) – не является формулой с ограниченной переменной
P(t) & ¬Q(t) – формула с ограниченной переменной
Слайд 16Ограниченные кванторы
Примеры:
∃x(x.Fund < 5) – квантор существования не ограничен
∃x(P(x) &
x.Fund < 5) – квантор существования ограничен
∀x(P(x)) → Q(x, y))
– квантор общности ограниченЕсли F(t) - ограниченная формула а G(t) – произвольная формула, то формула ∃t(F(t)& G(t)) называется формулой с ограниченным
квантором существования. Сама формула интерпретируется
ограниченным отношением.
Если F(t) - ограниченная формула, а G(t) – произвольная формула, то формула ∀t(F(t) → G(t)) называется формулой с ограниченным квантором общности. Сама формула интерпретируется ограниченным отношением
Слайд 17Доменное реляционное исчисление
(DRC)
Запрос имеет вид {x1,x2,...,xn | (F(x1,x2,...,xn)}
x1,x2,...,xn -
доменные переменные;
F(x1,x2,...,xn) - формула, в которой единственными свободными переменными являются
x1,x2,...,xn Ответ. Множество всех таких кортежей
Формула. Рекурсивно определяется через атомарные формулы и построением более сложных формул с помощью логических связок и кванторов точно так же, как и в TRC.
QBE. Является формальной основной языка QBE.
Слайд 18Примеры запросов в DRC
1) Проекция
Запрос. Вывести названия факультетов и имена
их деканов
{(y, z)|∃x∃u∃vFAC(x,y,z,u,v)}
2) Селекция и проекция
Запрос. Вывести названия факультетов корпуса
5 и их деканов{(y, z) | ∃x∃u∃vFAC(x,y,z,u,v) & u = 5}
3) Соединение, селекция и проекция
Запрос. Вывести имена факультетов корпуса 5 и имена их кафедр
{(y,n)|∃x∃f(∃z∃u∃v(FAC(x,y,z,u,v) & u=5) & ∃d∃h∃b∃uDEP(d,f,n,h,b,u) & x=f)}
FAC (FNo,Name,Dean,Bld,Fund) DEP(DNo,FNo,Name,Head,Bld,Fund)
x y z u v d f n h b u
Слайд 19
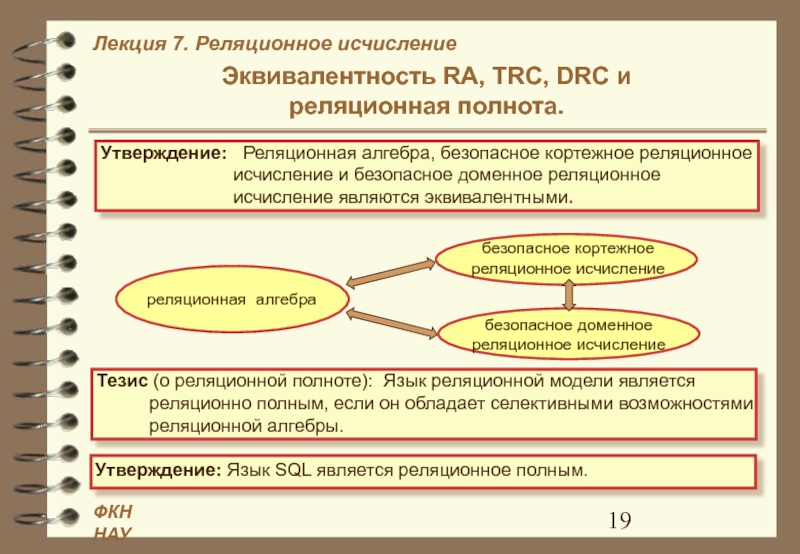
Эквивалентность RA, TRC, DRC и
реляционная полнота.
Тезис (о реляционной
полноте): Язык реляционной модели является реляционно полным, если он обладает
селективными возможностями реляционной алгебры. Утверждение: Реляционная алгебра, безопасное кортежное реляционное исчисление и безопасное доменное реляционное исчисление являются эквивалентными.
реляционная алгебра
безопасное кортежное реляционное исчисление
безопасное доменное реляционное исчисление
Утверждение: Язык SQL является реляционное полным.
Слайд 20Реляционное исчисление Кодда (СRС)
Является подмножеством исчисления предикатов
(1-го порядка)
Является кортежно-ориентированным
Решает
проблему различия между ппф и безопасными
формулами
Запросы являются безопасными
Является эквивалентным
реляционное алгебре; значит
обладает реляционной полнотойСлайд 21CRC – основные составляющие
Константы: 7, 'john', 3.14159 и т.д.
Кортежные
(строковые) переменные: t1, t2,... –
интерпретируются кортежами отношений.
Срезы кортежных переменных:
t.[i],…
i – компонента кортежной переменной. Предикатные символы: P, P1,...,Q, Q1,… Интерпретируются отношениями
Операторы (предикаты) сравнения : = {=, <, <=, >, >=, <>} и т.д.
Логические связки: ∨ (или), ∧(&) (и), ¬ (не ), → (влечет)
Кванторы: ∃(существует), ∀(для любого)
Слайд 22CRC - правильно определенные формулы
Термы:
P.t – терм значений:
P - предикат, t - кортежная переменная.
Если Р интерпретируется отношением R, то P.t означает t ∈ Rt[i] θ s[j], t[i] = c - термы соединений
Примеры: t1[3] = t2[1]; t4[7] = 15
Формулы, правильно определенные над строковой переменной:
Все входящие в формулу предикатные символы интерпретируются совместимыми по объединению отношениями.
В формулу входят только термы значений с единственной переменной.
Термы значений соединяются связками ∨, &, ¬. Причем, связке ¬ непосредственно предшествует связка &.
Примеры формул, правильно определенных над переменной t.
P1.t ∨ P2.t ∨ (P3.t & P4.t); (P1.t ∨ P2.t) & ¬P3.t.
Слайд 23Формула, правильно определенная
на кванторах
По сути, это частный случай
ограниченных кванторов существования и общности. Здесь формула F указывает ту
область, в пределах которой изменяется переменная, используемая в кванторах.Будем записывать эти формулы следующим образом:
∃F(G) и ∀F(G)
Пусть F – формула, правильно определенная над строковой переменной t, а G – формула, содержащая t в качестве свободной переменной, но не содержащая термов значений вида P.t. Тогда формулы:
∃t(F & G); ∀t(F → G)
называются правильно определенными на кванторах.
Примеры:
∃t((P.t ∨ Q.t) & ¬S.t) & t[2] = ‘john’ & t[5] = 1000)
∀t((P.t ∨ Q.t) & ¬S.t) → (t[2] = ‘john’ & t[5] = 1000))
Слайд 24Формула с областью определения
Формула W называется формулой с областью
определения, если она имеет вид:
W = U1 & U2 &…&
Un & V, n ≥ 1и обладает следующими свойствами:
Каждая формула Ui является правильно определенной над кортежной переменной ti.
Формула V либо пуста, либо обладает следующими свойствами:
Если в ней содержатся кванторы, то они правильно определены.
Каждая свободная переменная из V является одной из переменных формул U1, U2,…, Un
В V нет термов значений, содержащих свободные переменные.
Примеры: P.r & Q.s & R.t - декартово произведение
P.r & (r[3] = b) - селекция
P.r & Q.s & (r [2] = s[1]) - соединение
Слайд 25Альфа-выражения
Выражение (t1, t2,…, tk) : W называется простым альфа-выражением, если
выполнены следующие условия:
W – формула с областью определения.
t1, t2,…,
tk – последовательность кортежных переменных и срезов. Эти переменные должны быть свободными в W.Произвольное альфа-выражение определяется рекурсивно следующим образом:
Каждое простое альфа-выражение является альфа-выражением.
Пусть t = (t1, t2,…, tk). Если t : W1 и t : W2 – альфа-выражения, то выражения t : W1 ∨ W2, t : W1 & W2 и t : W1 & ¬W2 являются альфа-выражениями.
Слайд 26Язык ALPHA
Упрощенный синтаксис:
RANGE [ SOME
| ALL]
…
GET ( ) :
range – указание
имени кортежной переменной SOME | ALL – указывают, следует ли интерпретировать переменную с квантором существования или общности.
workspace – идентификатор, который именует временное рабочее отношение, содержащее результат выполнения команды Get.
target list – целевой список кортежных переменных и их срезов, указывающих столбцы, которые проецируются в результирующее отношение.
wff – правильно построенная формула кортежного реляционного исчисления
Слайд 27Примеры запросов в ALPHA и CRC
Запрос. Вывести названия факультетов и
их деканов
CRC: {f[2], f[3] | FAC.f}
ALPHA: RANGE FACULTY f
GET W(f.Name, f.Dean)
Запрос.
Вывести имя декана факультета CSF CRC: {f[3] | FAC.f & f[2] = ‘CSF’}
ALPHA: RANGE FACULTY f
GET W(f.Dean) : f.Name = ‘CSF’
Запрос. Вывести названия кафедр факультета CSF
CRC: {d[3] | DEP.d & ∃f(FAC.f & f[2] = ‘CSF’ & f[1] = d[2])}
ALPHA: RANGE FACULTY f SOME
RANGE DEPARTMENT d
GET W(d.Name) = f.Name = ‘CSF’ & f.FNo = d.DNo
Слайд 28Заключение
Реляционное исчисление является декларативным (не
процедурным) языком, в котором запросы
формулируются в терминах того, ЧТО требуется, а не КАК вычислить
требуемые значения.(Безопасное) реляционное исчисление и реляционная алгебра имеют одинаковую выразительную силу, и на их основании формулируется тезис о реляционной полноте.
Имеется возможность формулировать правильные, но не эффективные запросы. В связи с этим необходимы оптимизаторы.
Имеются языки непосредственно реализующие реляционное исчисление (ALPHA, QUEL), а также базирующиеся на кортежном исчислении (SQL) и доменном исчислении (QBE).
























![Реляционное исчисление Язык ALPHA Упрощенный синтаксис: RANGE [ SOME | ALL] …GET Язык ALPHA Упрощенный синтаксис: RANGE [ SOME | ALL] …GET ( ) : range – указание имени кортежной](/img/thumbs/c1f17e6cfa3b3af8bb8e10357c6e78d3-800x.jpg)
![Реляционное исчисление Примеры запросов в ALPHA и CRCЗапрос. Вывести названия факультетов и их Примеры запросов в ALPHA и CRCЗапрос. Вывести названия факультетов и их деканов CRC: {f[2], f[3] | FAC.f}ALPHA: RANGE FACULTY](/img/thumbs/a24d34b10162d4ef3c0894759ce3f279-800x.jpg)