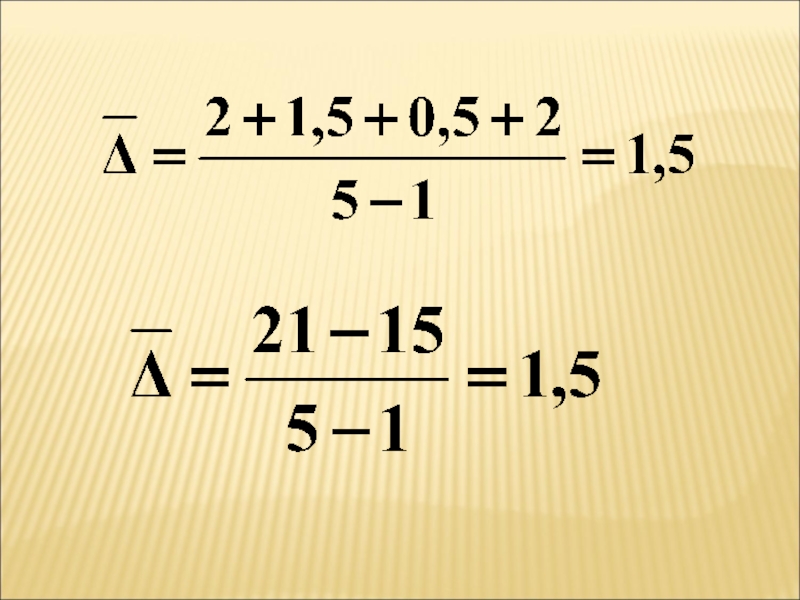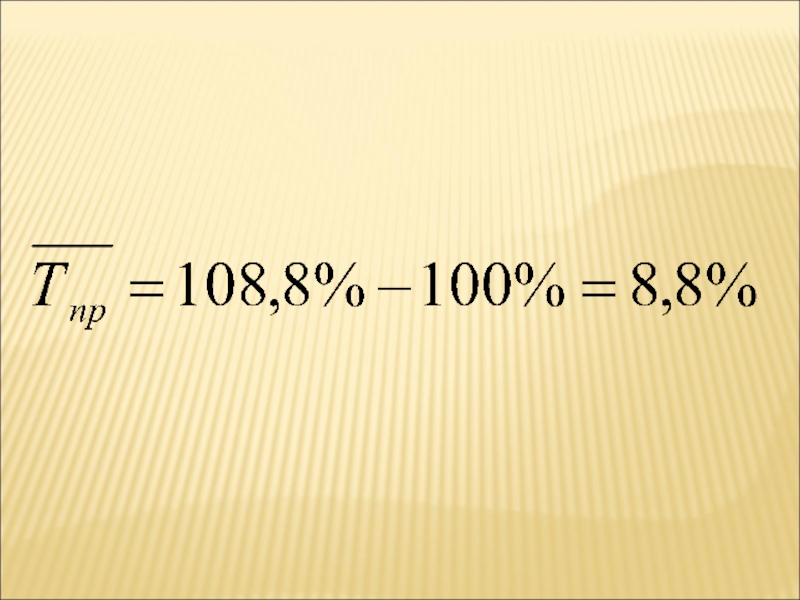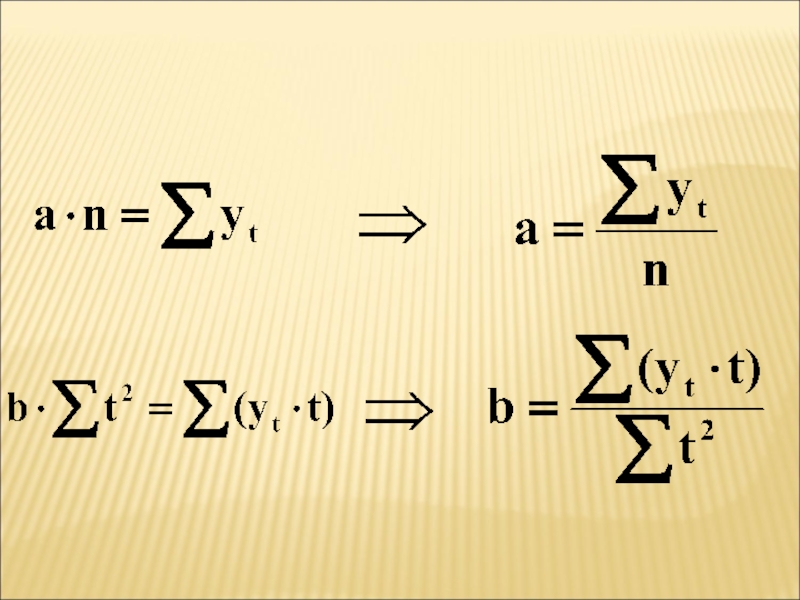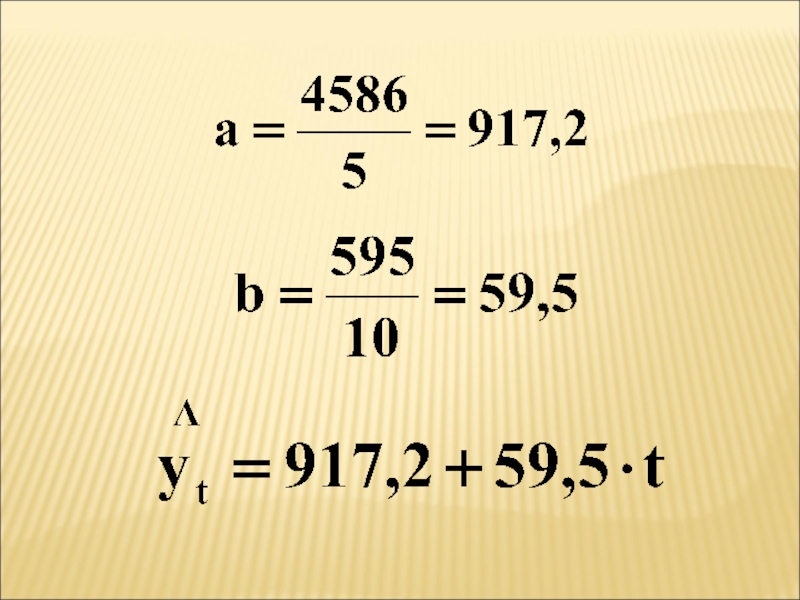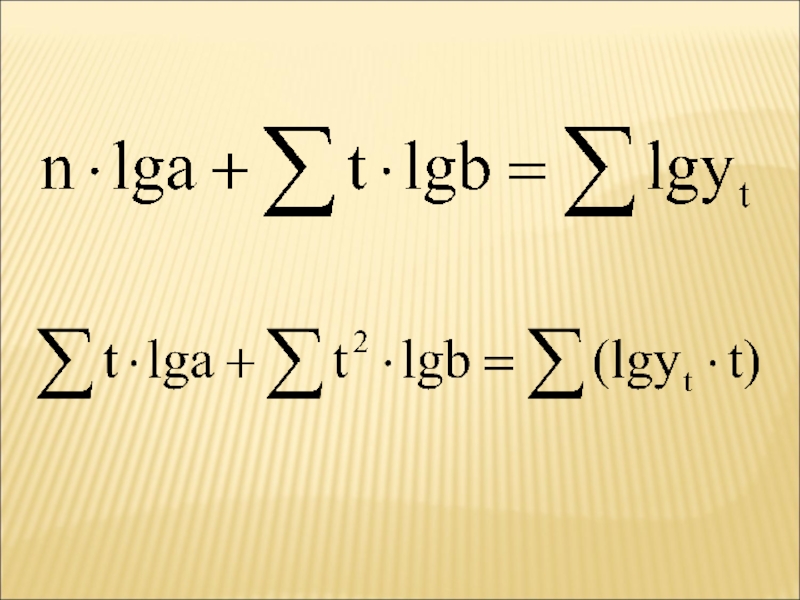Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ряды динамики
Содержание
- 1. Ряды динамики
- 2. Ряды динамики (временные ряды) применяются
- 3. РЯД ДИНАМИКИ последовательность изменяющихся во времени значений статистического показателя , расположенного в хронологическом порядке
- 4. Составными элементами ряда динамики являются показатели уровней
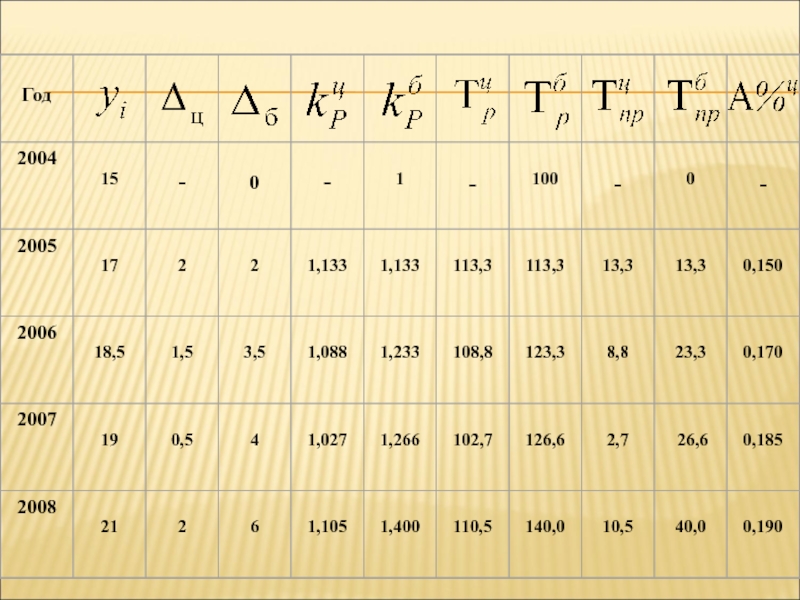
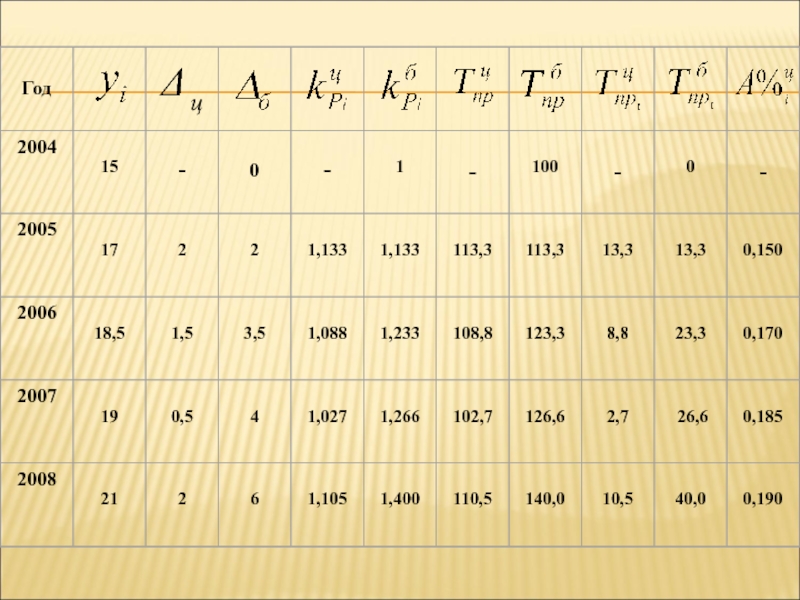
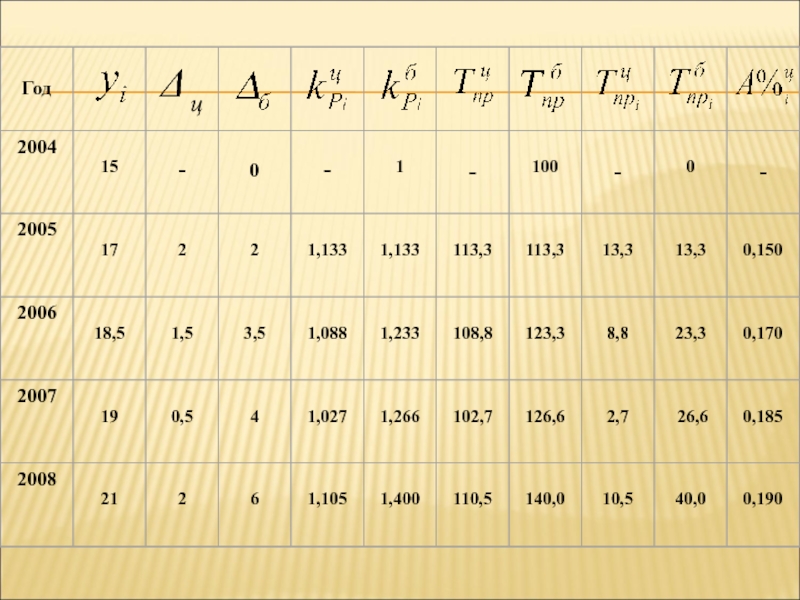
- 5. ПримерЗдесь t – время; yi – производство продукции, тыс. шт.
- 6. В зависимости от способа выражения уровней ряда ряды динамики делятся на ряды :
- 7. В зависимости от того , как выражают
- 8. Ряды динамики подразделяются на моментные и интервальные.Моментным
- 9. Интервальным называется такой ряд, абсолютные уровни которого
- 10. Выделяют также производные ряды динамики, которые состоят
- 11. Основные показатели, применяемые для анализа рядов динамики
- 12. Анализ скорости и интенсивности
- 13. Различают показатели изменения уровней ряда
- 14. Средние величины
- 15. К показателям изменения уровней
- 16. 1.Абсолютные приросты бывают цепными и базисными.
- 17. Базисный абсолютный прирост:где - базисный уровень ряда
- 18. Цепной абсолютный прирост:где - текущий
- 19. Слайд 19
- 20. 2. Коэффициент роста показывает, во сколько раз изменился
- 21. Цепной коэффициент роста:
- 22. Базисный коэффициент роста:
- 23. 3.Темпы роста – это коэффициенты роста, выраженные
- 24. Темп роста: а) базисный:
- 25. 4.Темп прироста используется для выражения величины абсолютного прироста уровней ряда динамики в относительных величинах:
- 26. Темп прироста показывает, на сколько процентов изменился
- 27. Базисный темп прироста
- 28. 5.Абсолютное значение одного процента
- 29. Содержание одного процента базисного прироста:
- 30. Содержание одного процента цепного прироста:
- 31. Слайд 31
- 32. Расчет среднего уровня ряда динамики
- 33. СРЕДНИЕ ХАРАКТЕРИСТИКИ РЯДА Средний уровень ряда динамики рассчитывается по формулам средней арифметической или средней хронологической
- 34. 1.Если ряд динамики является интервальным, то расчет среднего уровня ведется по формуле простой средней арифметической:
- 35. СРЕДНИЙ УРОВЕНЬ РЯДАДЛЯ ИНТЕРВАЛЬНЫХ РЯДОВ С РАВНЫМИ
- 36. Пример. Имеются следующие данные о динамике производства
- 37. 2. Если ряд динамики является моментным с различными
- 38. Пример. Известна списочная численность персонала организации по
- 39. С неравными интервалами времени Эта
- 40. 3.Если ряд динамики является моментным с равноотстоящими уровнями, то используется средняя хронологическая простая:где n-количество дат
- 41. Пример. Известны товарные остатки магазина на 1-е
- 42. Средний абсолютный прирост определяется как простая средняя
- 43. Средний абсолютный прирост показывает, на сколько в
- 44. Слайд 44
- 45. Слайд 45
- 46. Среднегодовой коэффициент роста определяется как средняя геометрическая
- 47. Если цепные коэффициенты роста определялись для рядов с равностоящими интервалами, то применяется простая средняя геометрическая величина
- 48. Средний коэффициент роста рассчитывается по формуле средней геометрической из цепных коэффициентов роста:
- 49. Слайд 49
- 50. Слайд 50
- 51. С неравными интервалами времени Взвешенная средняя геометрическая
- 52. Среднегодовой темп роста определяется умножением среднегодового коэффициента
- 53. СРЕДНИЙ ТЕМП ПРИРОСТАПоказывает, на сколько процентов увеличивается
- 54. Слайд 54
- 55. Проблема сопоставимости уровней рядов динамикиСмыкание рядов динамики
- 56. Поскольку ряды динамики формируются на протяжении длительных периодов времени, их уровни часто оказываются несопоставимыми
- 57. ПричиныИзменение ценИзменение методики расчета показателейИзменение «границ» (организа- ционных, административных)
- 58. Для обеспечения сопоставимости данных часто применяется метод
- 59. Слайд 59
- 60. Слайд 60
- 61. Слайд 61
- 62. Слайд 62
- 63. Анализ основной тенденции рядов динамики
- 64. Уровни рядов динамики формируются под
- 65. 1. Определяющие факторы –
- 66. Слайд 66
- 67. 2. Сезонные факторы – факторы, которые вызывают сезонные колебания относительно основной тенденции
- 68. Слайд 68
- 69. 3. Случайные факторы – факторы, которые вызывают случайные колебания уровней ряда (например, погодный фактор)
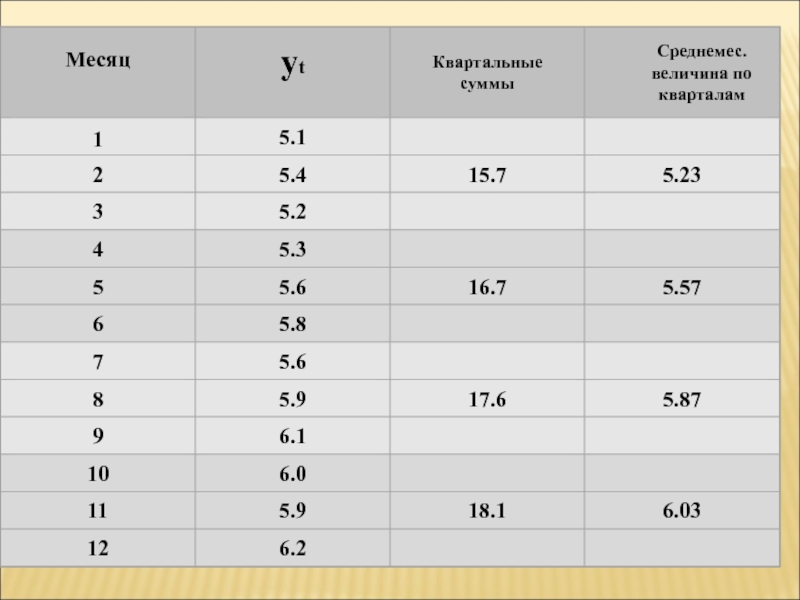
- 70. Метод укрупнения интервалов
- 71. Метод укрупнения интервалов – замена исходных уровней ряда средними величинами, которые рассчитываются для укрупненных интервалов
- 72. Слайд 72
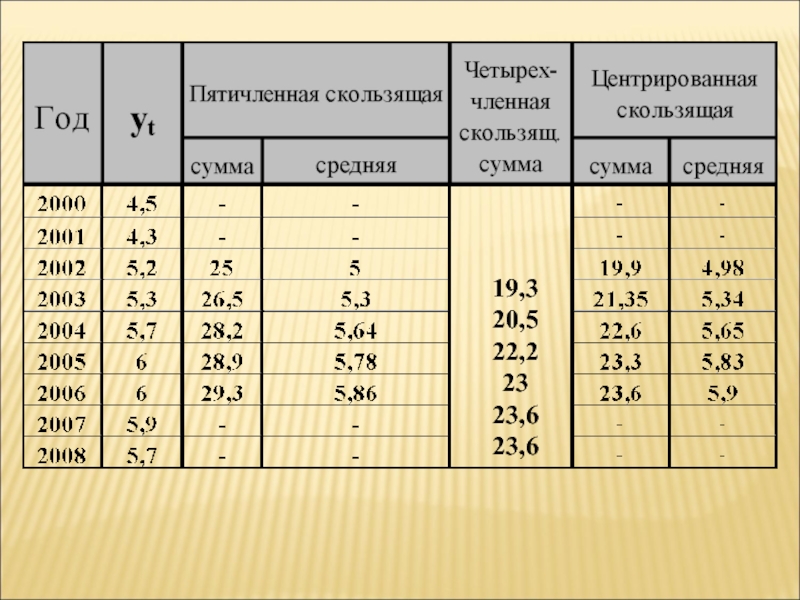
- 73. Метод скользящей средней
- 74. Метод скользящей средней– замена исходных уровней
- 75. 19,320,522,22323,623,6
- 76. Аналитическое выравнивание рядов динамики
- 77. Уровни ряда рассматриваются как некоторая функция от времени:
- 78. Процедура выравнивания в этом случае
- 79. Рассмотрим данный метод на примере линейного уравнения
- 80. Линейный тренд лучше всего использовать в тех
- 81. Параметры a и b определяются при помощи метода наименьших квадратов (МНК)
- 82. Применение метода МНК дает следующую систему уравнений
- 83. Данную систему уравнений можно существенно упростить, если
- 84. Если ряд содержит нечетное число уровней, то
- 85. Если ряд содержит четное число уровней, то
- 86. Слайд 86
- 87. Слайд 87
- 88. Слайд 88
- 89. Слайд 89
- 90. Выравнивание по параболе второго порядка:
- 91. Выравнивание по параболе второго порядка производится,
- 92. Слайд 92
- 93. Для определения параметров применяется метод наименьших квадратов:
- 94. Выравнивание по гиперболе применяется в тех случаях, когда в развитии ряда динамики происходит насыщение
- 95. Слайд 95
- 96. Для определения параметров используется МНК:
- 97. Выравнивание ряда динамики при помощи
- 98. Для определения параметров функция приводится предварительно к
- 99.
- 100. С’est toutMerci beaucoup!
- 101. Скачать презентанцию
Ряды динамики (временные ряды) применяются для изучения изменения явлений во времени. Ряд динамики представляет собой ряд числовых значений определенного статистического показателя в последовательные моменты или периоды времени
Слайды и текст этой презентации
Слайд 3РЯД ДИНАМИКИ
последовательность изменяющихся во времени значений статистического показателя
, расположенного в хронологическом порядке
Слайд 4Составными элементами ряда динамики являются показатели уровней ряда и периоды
времени (годы , кварталы , сутки) или моменты (даты) времени.
Уровни ряда обычно обозначаются через «y» , моменты или периоды времени , к которым относятся уровни – через «t»Слайд 7В зависимости от того , как выражают уровни ряда (на
начало месяца или за период),выделяют моментные и интервальные ряды динамики
В
зависимости от расстояния между уровнями ряды динамики бывают с равностоящими и неравностоящими уровнями во времениВ зависимости от наличия основной тенденции изучаемого процесса ряды динамики подразделяются на стационарные и нестационарные
Слайд 8Ряды динамики подразделяются на моментные и интервальные.
Моментным называется ряд, абсолютные
уровни которого характеризуют величину явления по состоянию на определенные моменты
времени или даты. (Например, численность населения, уровни товарных остатков)Слайд 9Интервальным называется такой ряд, абсолютные уровни которого представляют собой итоговые
величины за некоторые интервалы времени (например, производство продукции за месяц;
число родившихся за месяц, год).Особенностью интервальных рядов является то, что их уровни можно дробить и складывать
Слайд 10Выделяют также производные ряды динамики, которые состоят из средних или
относительных величин. Они рассчитываются на основе моментных или интервальных рядов.
(Например, среднегодовая численность населения)Слайд 12 Анализ скорости и интенсивности явления во
времени осуществляется с помощью статистических показателей , которые получаются
в результате сравнения уровней между собой . Сравниваемый уровень называют отчётным , а уровень , с которым происходит сравнение – базиснымСлайд 14Средние величины
Ряды динамики
Абсолютные величины
Относительные величины
Интервальныеи Моментные
Интервальные
Слайд 15
К показателям изменения уровней ряда относятся абсолютный
прирост, коэффициент роста и прироста, темп роста и прироста, абсолютное
значение 1% прироста (роста)Слайд 16 1.Абсолютные приросты бывают цепными и базисными. Абсолютный прирост показывает,
на сколько изменился изучаемый показатель по сравнению с предыдущим или
базисным периодом времениСлайд 20 2. Коэффициент роста показывает, во сколько раз изменился изучаемый показатель по
сравнению с предыдущим периодом времени или с базисным периодом времени.
Соответственно коэффициент роста может быть цепным и базиснымСлайд 233.Темпы роста – это коэффициенты роста, выраженные в процентах (они
также могут быть цепными, базисными и средними):
Tр= Kp • 100
(%)Слайд 254.Темп прироста используется для выражения величины абсолютного прироста уровней ряда
динамики в относительных величинах:
Слайд 26Темп прироста показывает, на сколько процентов изменился изучаемый показатель по
сравнению с предыдущим периодом времени или с базисным периодом времени.
Цепной
темп прироста:Слайд 28 5.Абсолютное значение одного процента прироста А% показывает,
сколько абсолютных единиц содержится в 1% прироста
Слайд 33СРЕДНИЕ ХАРАКТЕРИСТИКИ РЯДА
Средний уровень ряда динамики рассчитывается по
формулам средней арифметической или средней хронологической
Слайд 341.Если ряд динамики является интервальным, то расчет среднего уровня ведется
по формуле простой средней арифметической:
Слайд 35СРЕДНИЙ УРОВЕНЬ РЯДА
ДЛЯ ИНТЕРВАЛЬНЫХ РЯДОВ
С РАВНЫМИ ИНТЕРВАЛАМИ ВРЕМЕНИ
Простая средняя арифметическая
= где n - количество периодов времени
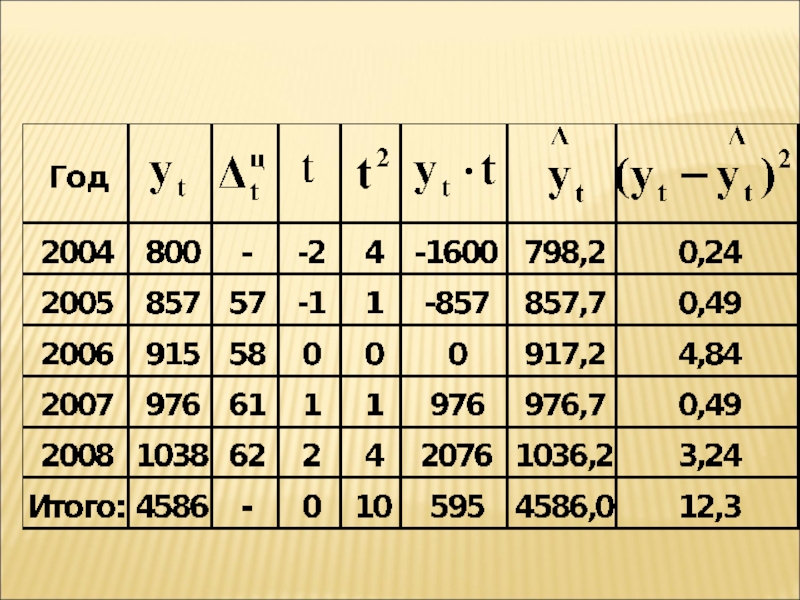
Слайд 36Пример. Имеются следующие данные о динамике производства продукции предприятием за
2004-2008 гг., тыс. шт.
Определить среднегодовое производство продукции за 2004-2008 гг.
тыс.
шт.Слайд 372. Если ряд динамики является моментным с различными интервалами времени между
датами, то для расчета среднего уровня используется средняя арифметическая взвешенная:
где – продолжительность i-го интервала времени (интервал времени между двумя соседними значениями;
- средний уровень ряда для i-го интервала времени
Слайд 38Пример. Известна списочная численность персонала организации по состоянию на следующие
даты (человек) :
Среднесписочная численность персонала за год составляет:
чел.
Слайд 39 С неравными интервалами времени
Эта формула иногда дается
как взвешенная средняя хронологическая
=
где
ti – период времени между двумя соседними значениямиСлайд 40 3.Если ряд динамики является моментным с равноотстоящими уровнями, то
используется средняя хронологическая простая:
где n-количество дат
Слайд 41Пример. Известны товарные остатки магазина на 1-е число каждого месяца
(тыс. руб.) :
Средний уровень товарных остатков за первый квартал составил:
тыс.
руб.Слайд 42Средний абсолютный прирост определяется как простая средняя арифметическая величина из
цепных абсолютных приростов и показывает , на сколько в среднем
изменялся показатель в течение изучаемого периода времениСлайд 43Средний абсолютный прирост показывает, на сколько в среднем изменялся изучаемый
показатель при переходе от предыдущего периода времени к смежному последующему
периоду временигде n – число уровней ряда динамики;
S = n - 1 – количество цепных приростов
Слайд 46
Среднегодовой коэффициент роста определяется как средняя геометрическая из цепных коэффициентов
роста и показывает , сколько в среднем составлял рост показателя
Слайд 47
Если цепные коэффициенты роста определялись для рядов с равностоящими интервалами,
то применяется простая средняя геометрическая величина
Слайд 48 Средний коэффициент роста рассчитывается по формуле средней геометрической из цепных
коэффициентов роста:
Слайд 51С неравными интервалами времени
Взвешенная средняя геометрическая
=
где ki – коэффицент роста;
ti
– период времени между двумя соседними значениямиСлайд 52
Среднегодовой темп роста определяется умножением среднегодового коэффициента роста на 100
и показывает , сколько процентов в среднем составлял рост показателя
Слайд 53СРЕДНИЙ ТЕМП ПРИРОСТА
Показывает, на сколько процентов увеличивается (или уменьшается) уровень
по сравнению с предыдущем в среднем за единицу времени:
Слайд 56 Поскольку ряды динамики формируются на протяжении длительных периодов
времени, их уровни часто оказываются несопоставимыми
Слайд 57
Причины
Изменение цен
Изменение методики расчета показателей
Изменение
«границ» (организа- ционных, административных)
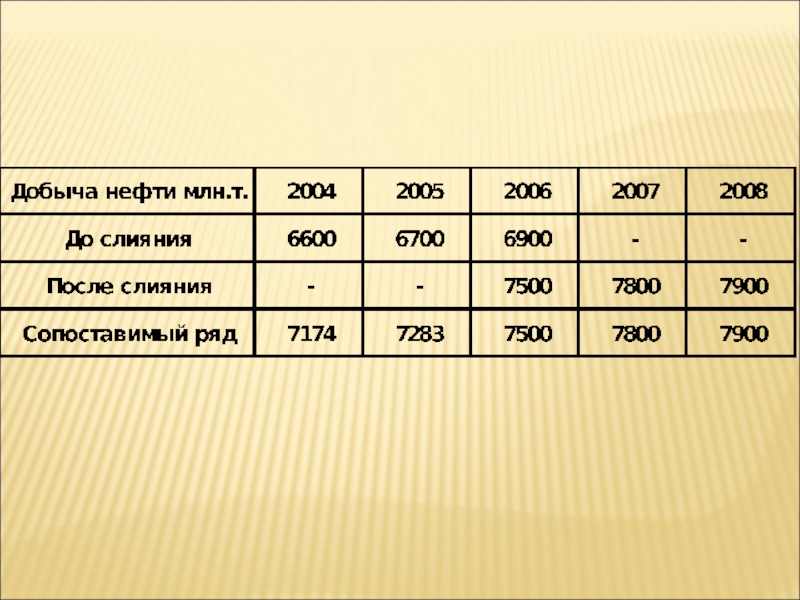
Слайд 58Для обеспечения сопоставимости данных часто применяется метод смыкания рядов динамики.
Для смыкания ряда динамики необходимо иметь переходное звено. (Переходное звено
– это период времени, для которого изучаемый показатель рассчитан как по старой методике (в старых границах), так и по новой методике (в новых границах).Для переходного звена рассчитывается коэффициент, действие которого распространяется на все предшествующие периоды времени
Слайд 64 Уровни рядов динамики формируются под воздействием большого числа
факторов. Их можно разделить на 3 группы
Слайд 65 1. Определяющие факторы – факторы, которые оказывают
постоянное и сильное воздействие на изучаемый показатель. Они определяют основную
тенденцию (тренд) ряда динамикиСлайд 67 2. Сезонные факторы – факторы, которые вызывают сезонные колебания
относительно основной тенденции
Слайд 69 3. Случайные факторы – факторы, которые вызывают случайные колебания
уровней ряда (например, погодный фактор)
Слайд 71 Метод укрупнения интервалов – замена исходных уровней ряда средними
величинами, которые рассчитываются для укрупненных интервалов
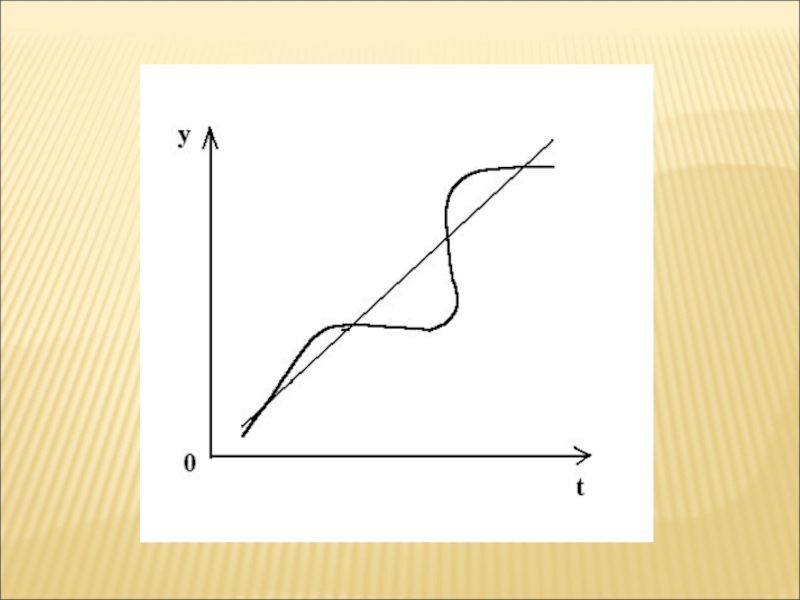
Слайд 74 Метод скользящей
средней– замена исходных уровней ряда средними величинами,
которые рассчитываются для последовательно смещающихся интервалов времени
Слайд 78 Процедура выравнивания в этом случае сводится:
⮚ к выбору вида
функции;
⮚ к определению параметров функции;
⮚ к получению выравненных значений
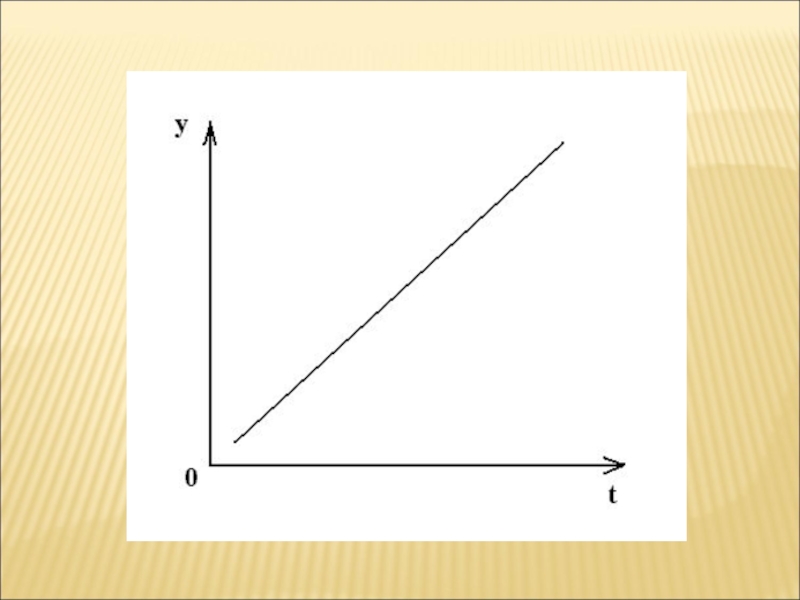
уровней ряда на основе функцииСлайд 79Рассмотрим данный метод на примере линейного уравнения (тренда):
где a и b – параметры;
t – времяСлайд 80Линейный тренд лучше всего использовать в тех случаях, когда предварительный
анализ показывает, что уровни ряда изменяются с примерно одинаковой скоростью,
т.е. когда цепные абсолютные приросты примерно равны между собойСлайд 83Данную систему уравнений можно существенно упростить, если пронумеровать время таким
образом, чтобы
Слайд 84Если ряд содержит нечетное число уровней, то центральный уровень ряда
нумеруется нулем. Уровни в сторону убывания времени нумеруются -1; -2;
-3…, в сторону возрастания времени 1; 2; 3…Слайд 85Если ряд содержит четное число уровней, то ближайшие к центру
уровни ряда нумеруются: -1 и 1, далее нумерация как для
ряда с нечетным числом уровней только с шагом 2: …-5; -3; -1; +1; +3; +5…Слайд 90 Выравнивание по параболе второго порядка:
где b – скорость изменения уровней ряда динамики
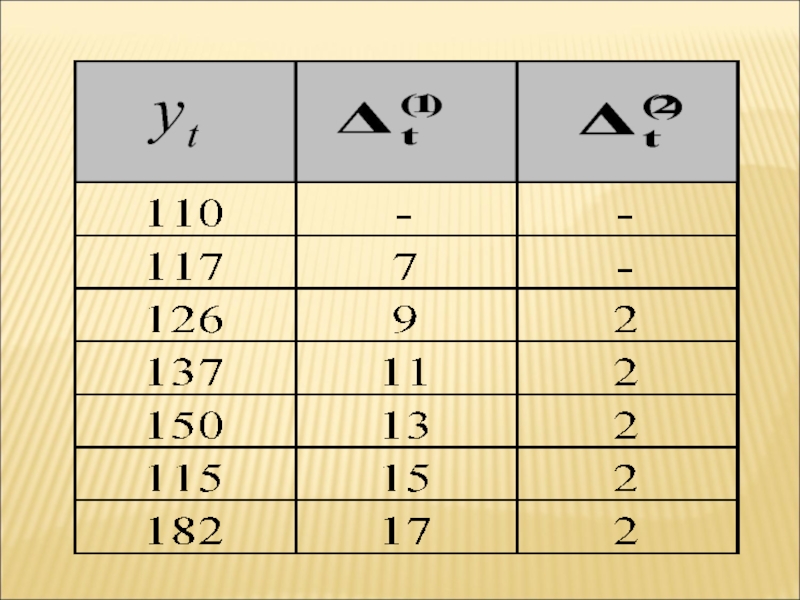
c – ускорениеСлайд 91 Выравнивание по параболе второго порядка производится, когда предварительный анализ
показывает, что вторые разности примерно равны между собой
- первая разность;- вторая разность
Слайд 94 Выравнивание по гиперболе применяется в тех случаях, когда
в развитии ряда динамики происходит насыщение
Слайд 97 Выравнивание ряда динамики при помощи показательных функций или
экспоненты применяется, когда предварительный анализ показывает: уровень ряда динамики меняется
с приблизительно одинаковыми цепными коэффициентами роста. При этом коэффициент b интерпретируется как средний коэффициент ростаСлайд 98Для определения параметров функция приводится предварительно к линейному виду при
помощи логарифмирования левой и правой частей уравнения
При этом мы находим
не a и b, а lga и lgb