Термодинамика

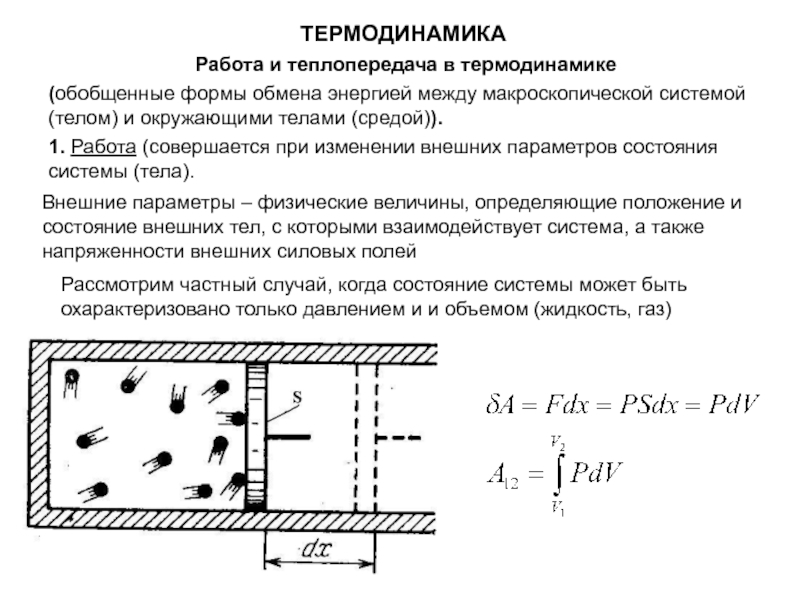
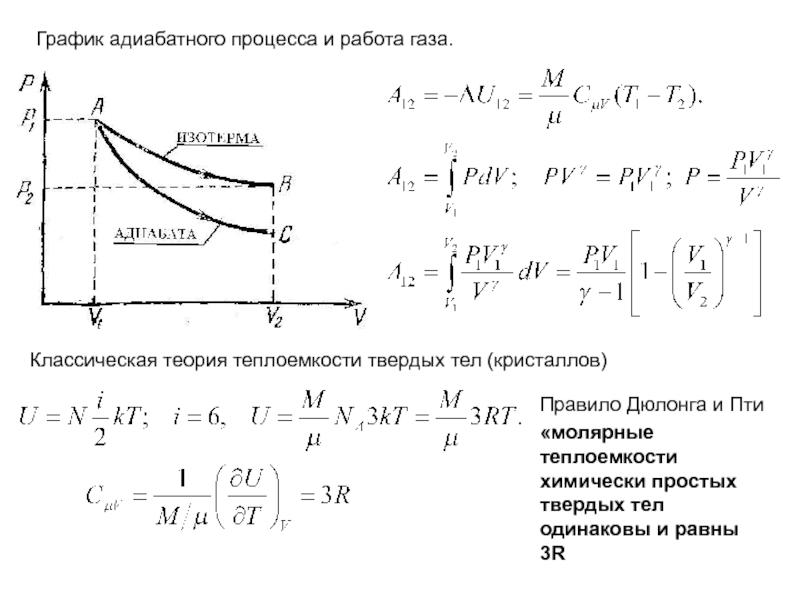
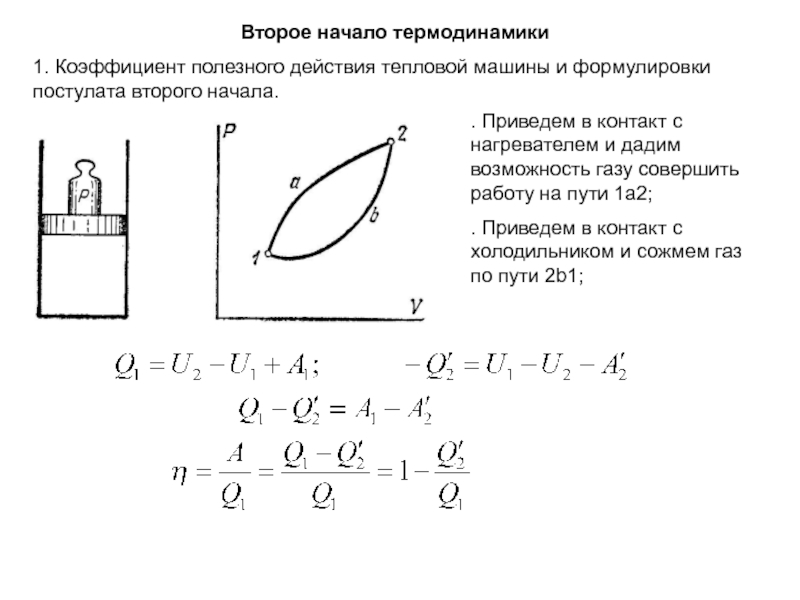
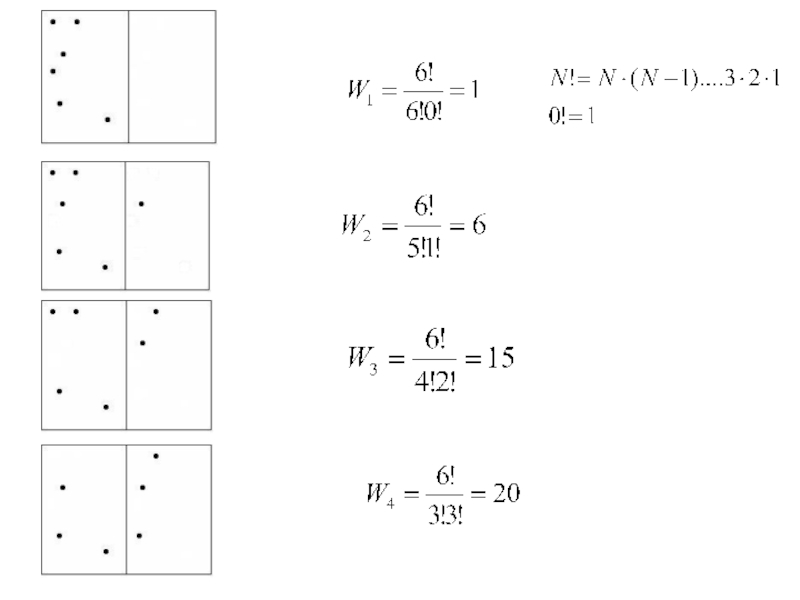
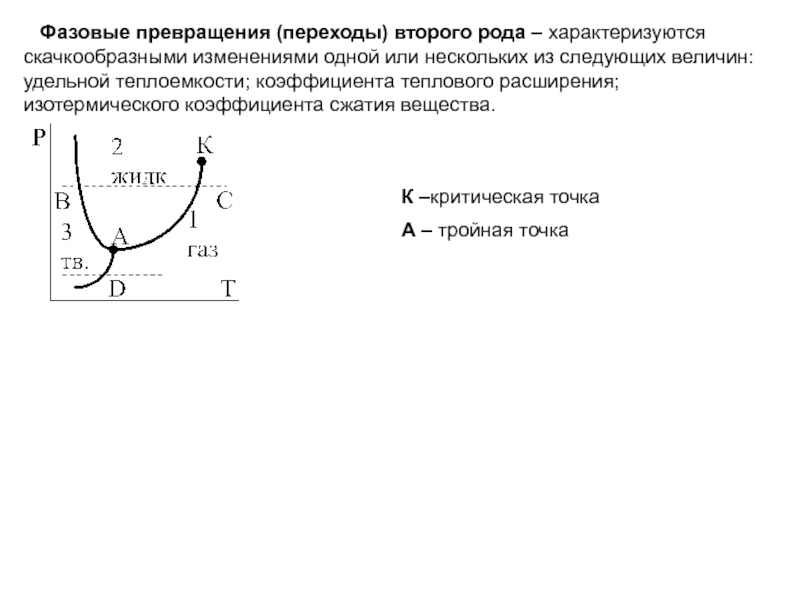
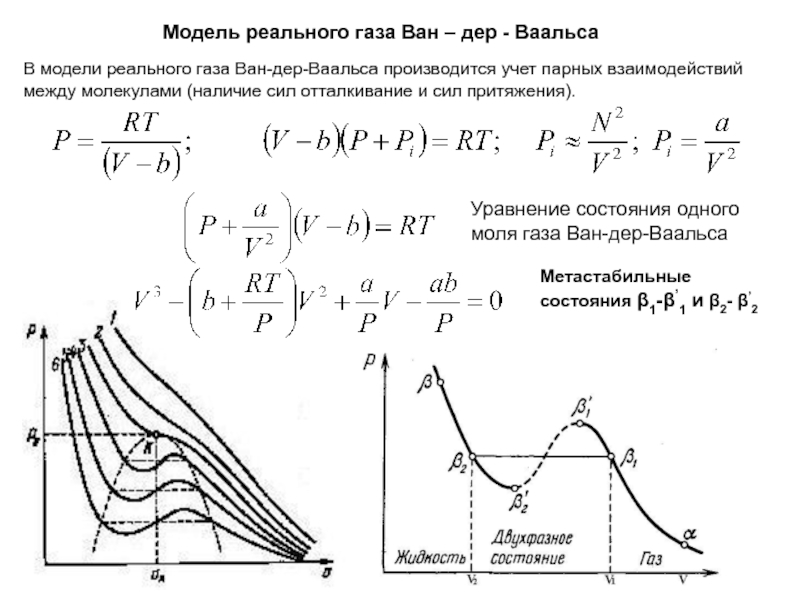
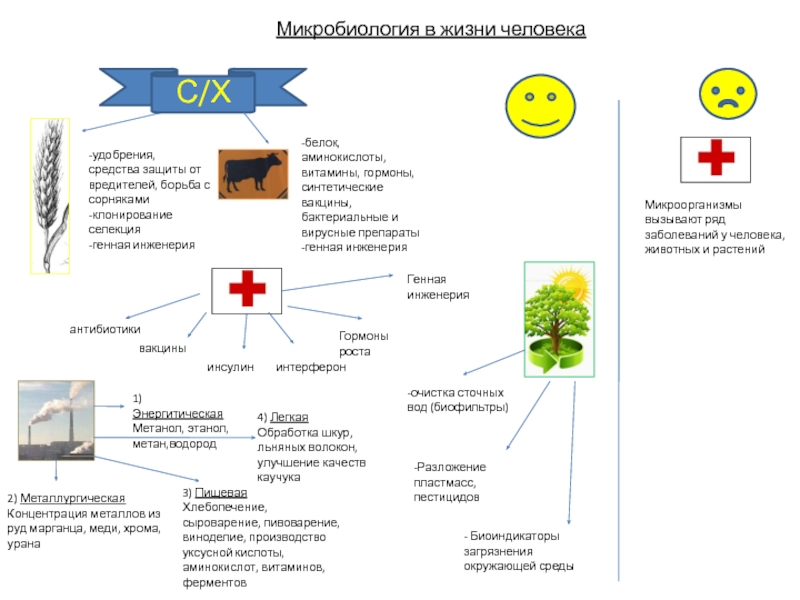
макроскопической системой (телом) и окружающими телами (средой)).
1. Работа (совершается при

изменении внешних параметров состояния системы (тела).

Внешние параметры – физические величины, определяющие положение и состояние внешних тел, с которыми взаимодействует система, а также напряженности внешних силовых полей

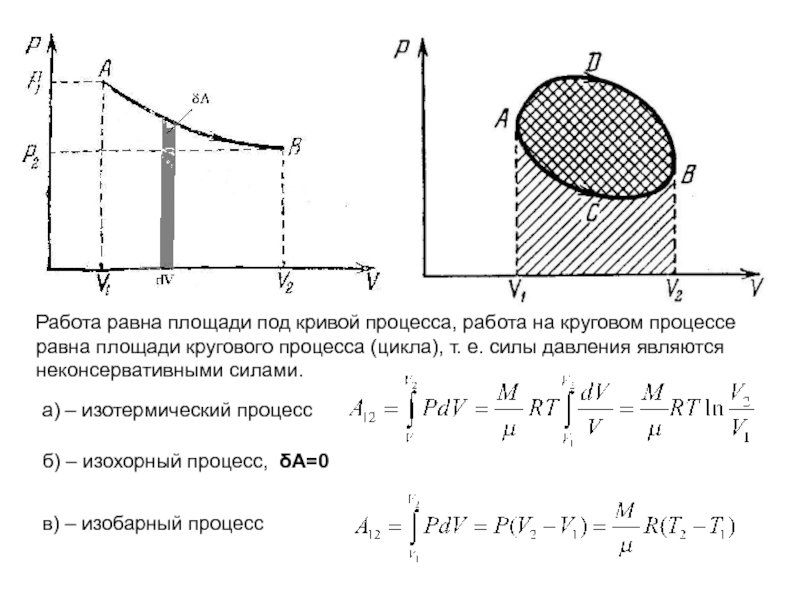
Рассмотрим частный случай, когда состояние системы может быть охарактеризовано только давлением и и объемом (жидкость, газ)

равна площади кругового процесса (цикла), т. е. силы давления являются

неконсервативными силами.

а) – изотермический процесс

б) – изохорный процесс, δА=0

в) – изобарный процесс

лежит прямое взаимодействие между частицами системы и частицами среды и

который не сопровождается изменением внешних параметров.
Количество энергии, передаваемое в ходе теплообмена называется количеством тепла δQ, Q12.

Теплоемкость

а) полная, Дж/К

б) молярная, Дж/моль·К

в) удельная, Дж/кг·К

Виды макросистем:
1. изолированная (замкнутая), δА=0, δQ=0.
2. теплоизолированная (адиабатическая), δQ=0, δА≠0.
3. тепловые резервуары, δА=0, δQ≠0.

на круговом процессе, к работе, совершенной системой в ходе этого

же кругового процесса, одинаково для всех систем и всех круговых процессов.

2. Для некруговых процессов

Количество тепла, сообщенное системе, идет на приращение внутренней энергии системы и на совершение системой работы над внешними телами.

В случае идеального газа

Для изопроцессов в газе:
- изотермический - изохорный
- изобарный

и его уравнения

(кристаллов)
Правило Дюлонга и Пти
«молярные теплоемкости химически простых твердых тел одинаковы

и равны 3R

постулата второго начала.
. Приведем в контакт с нагревателем и дадим

возможность газу совершить работу на пути 1а2;
. Приведем в контакт с холодильником и сожмем газ по пути 2b1;

результатом которого было бы производство работы за счет охлаждения теплового

резервуара»

Рудольф Клаузиус 1850 г. «теплота не может самопроизвольно переходить от тела менее нагретого к телу более нагретому»

2. Обратимые и необратимые процессы
«обратимым называется процесс, после проведения которого в прямом и обратном направлениях в окружающих систему телах не остается никаких изменений»

Всякий равновесный процесс является обратимым, а, следовательно, круговой процесс, образованный равновесными процессами, может происходить как в прямом, так и в обратном направлениях.

Т1, получает от нагревателя Q1;
(2-3) и (4-1) – соответственно адиабатное

расширение и сжатие, А23 = -А41;
(3-4) – изотермическое сжатие при Т2, отдает холодильнику Q′2;

«коэффициент полезного действия тепловой машины, работающей по циклу Карно, зависит только от температур Т1 и Т2 нагревателя и холодильника, но не зависит от устройства машины, а также от вида используемого рабочего вещества»

средой энергией в процессе теплопередачи
Оценим верхний предел К.П.Д. тепловой машины
Вторая

теорема Карно «КПД всякой тепловой машины не может превосходить КПД идеальной машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника»

обратного процесса
Это возможно только в случае, когда
Приведенное количество тепла, полученное

системой в ходе обратимого процесса, не зависит от пути перехода, а определяется лишь начальным и конечным состояниями системы

произвольной постоянной. Разность энтропий в двух равновесных состояниях 2 и

1 равна приведенному количеству тепла, которое надо сообщить системе, чтобы перевести ее из состояния 1 в состояние 2 по любому обратимому пути.

Энтропия одного моля идеального газа

процесс перехода 1I2 – необратимый.
Процесс 2 II 1 - обратимый
Если

система адиабатически изолирована, то δQ=0

Энтропия адиабатически изолированной системы не может убывать; она либо возрастает, либо остается постоянной.

максимуму». Когда будет достигнут этот максимум, во Вселенной прекратятся какие

бы то ни было процессы.

Ошибка Клаузиуса в том, что он распространил закон, сформулированный для ограниченных систем на всю Вселенную, для чего нет оснований.

1. Энтальпия

Для равновесного процесса dQ = TdS

Т.к. TdS=dQ, то при изобарном процессе dI = δQ

Энтальпия – функция состояния, приращение которой в равновесном процессе при постоянном давлении равно количеству тепла Q, полученному системой. (энтальпия – тепловая функция или теплосодержание).

= -δA. Т.е. А = Ψ1 - Ψ2
«свободная энергия –

функция состояния системы, убыль которой в равновесном изотермическом процессе равна работе, совершенной системой».

3. Термодинамический потенциал

Введение термодинамических функций позволяет получить канонические уравнения состояния вещества, которые содержат полные сведения о термических и калорических свойствах вещества.

системе происходят в направлении возрастания энтропии. При достижении максимума энтропии

(т.е. равновесного состояния) в системе должны прекратиться всякие процессы, что противоречит представлениям молекулярно – кинетической теории.

Пусть имеется сосуд, разделенный перегородкой АБ на две равные части, и в объеме I находится N молекул. Уберем перегородку АБ.

В конечном итоге установится динамическое равновесие, когда ==N/2

Принципиально возможна флуктуация, когда все молекулы самопроизвольно соберутся в одной половине сосуда. Почему же подобные процессы никогда не наблюдаются? Рассчитаем вероятность подобного процесса.

Для одной молекулы

Для двух молекул

Для 10 молекул

– объем какой – либо его части, тогда вероятность того,

что в объеме V окажутся все N молекул

В состоянии равновесия все флуктуации малы и равновероятны в большую и меньшую сторону. Если же создать неравновесное состояние, то в подавляющем большинстве случаев система самопроизвольно будет переходить в состояние с большей вероятностью. В термодинамике это процесс, сопровождающийся ростом энтропии. Поэтому можно ожидать, что между энтропией системы в каждом состоянии и вероятностью того же состояния должна существовать однозначная связь. (Больцман)

Связь должна быть универсальной т.е. одной и той же для любых макросистем

Рассмотрим две независимые подсистемы в состояниях с вероятностями Р1 и Р2

Объединим их в одну систему, тогда

при любых Р1 и Р2

f(P1)+f(P2)=const
P1⋅P2=const
Дифференцируя эти соотношения, получим
Решая это уравнение относительно переменной Р, установим

связь между энтропией и вероятностью

Произведем почленное деление

Постоянная интегрирования С должна равняться нулю, и, окончательно

разность энтропий системы в двух состояниях и логарифм отношения ее

вероятностей в тех же состояниях. Для этого воспользуемся моделью идеального газа и рассмотрим изотермическое расширение одного моля от объема V1 до объема V2.

Вероятность того, что все N молекул, находящихся в объеме VO, окажутся в объеме V определяется соотношением:

Для нахождения отношения вероятностей воспользуемся приведенным выражением, полагая сначала V=V1, а затем V=V2

-постоянная Больцмана

(статистический вес).
Микросостояние системы задается указанием значений координат и импульсов

всех частиц системы (детальное описание).

Макросостояние системы задается указанием значений ее макропараметров, которые определяются в основном концентрацией частиц и их усредненными характеристиками. При этом одно и тоже макросостояние возникает при самых различных значениях характеристик конкретных частиц.

Для того, чтобы можно было количественно рассчитать вероятность возникновения того или иного макросостояния введем понятие фазового пространства (мысленное 6ти-мерное пространство координат и импульсов) и фазовой ячейки.

Пронумеруем все частицы и будем считать, что координаты и импульс частицы определены, если указано, в какой фазовой ячейке она находится.
Таким образом микросостояние системы определено, если указано какие именно частицы находятся в каждой фазовой ячейке.
Макросостояние определено, если указано сколько частиц находится в каждой фазовой ячейке.

этого разобьем мысленно объем V на малые ячейки V1,V2,…,Vm.
Если

размеры ячеек одинаковы и отсутствуют внешние силовые поля, то математическая вероятность любого микросостояния одинакова и равна (р1)N, где р1=V1/V, а полное число молекул N.

Каждое макроскопическое состояние может быть реализовано определенным количеством различных микросостояний, поэтому математическая вероятность макросостояния будет в W раз больше вероятности микросостояния, где W – термодинамическая вероятность макросостояния.

Термодинамическая вероятность макросостояния равна количеству различных микросостояний, реализующих данное макросостояние.

ячейки
число молекул

Для расчета W необходимо рассчитать число перестановок молекул между ячейками

Закон возрастания энтропии утрачивает свою абсолютность и становится статистическим законом.
2.

За каким-либо заданным состоянием системы будут следовать состояния еще более вероятные, если и не с необходимостью, то в подавляющем большинстве случаев.

Тепловая теорема Нернста (1906 г.)
При приближении к абсолютному нулю энтропия стремится к определенному конечному пределу, при этом все процессы при абсолютном нуле температур, переводящие систему из одного равновесного состояния в другое равновесное состояние, происходят без изменения энтропии.
Если условиться энтропию всякой равновесной системы при абсолютном нуле температур считать равной нулю, то неоднозначность в определении энтропии исчезает. Таким образом определенную энтропию принято называть абсолютной.
При приближении к абсолютному нулю абсолютная энтропия системы стремится также к нулю, независимо от того, какие значения принимают при этом все параметры, характеризующие состояние системы.

не может быть истолкована классически. Объясняет ее содержание квантовая механика
Фазы

и фазовые превращения
Фазой называется макроскопическая физически однородная часть вещества, отделенная от остальных частей системы границами раздела, так что она может быть извлечена из системы механическим путем.
Условия равновесия системы, состоящей из нескольких фаз:
Механическое равновесие
Тепловое равновесие
Равновесие по отношению к взаимным превращениям фаз (неизменность масс всех фаз)

Следствие из теоремы Нернста: теплоемкости всех тел должны стремиться к нулю при приближении к абсолютному нулю температур.

Фазовые превращения (переходы) первого рода - характеризуются скачкообразным изменением либо удельной энтропии, либо удельного объема, либо обеих величин вместе.

изменениями одной или нескольких из следующих величин: удельной теплоемкости; коэффициента

теплового расширения; изотермического коэффициента сжатия вещества.

К –критическая точка
А – тройная точка

газа Ван-дер-Ваальса производится учет парных взаимодействий между молекулами (наличие сил

отталкивание и сил притяжения).

Уравнение состояния одного моля газа Ван-дер-Ваальса

Метастабильные состояния β1-β’1 и β2- β’2

обусловленные электрическим взаимодействием между зарядами, образующими атомы и молекулы, и

создающими внутреннее (молекулярное) давление. Поэтому внутренняя энергия газа Ван-дер-Ваальса складывается из кинетической энергии молекул и потенциальной энергии их взаимодействия.

Приращение потенциальной энергии можно вычислить через работу против сил молекулярного давления при увеличении объема газа