Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Механические свойства сред
Содержание
- 1. Механические свойства сред
- 2. Механика (от греч. mechanike – искусство построения
- 3. МЕХАНИЧЕСКИЕ СВОЙСТВА материалов определяют их поведение под действием механической нагрузки.
- 4. Большое значение для врача имеет механика жидкостей
- 5. 1. Особенности структуры и молекулярного движения
- 6. Жидкость - это агрегатное состояние вещества, промежуточное
- 7. Существование у вещества нескольких агрегатных состояний обусловлено
- 8. Основные положения молекулярно-кинетической теории (МКТ):
- 9. Силы, действующие между двумя молекулами, зависят от
- 10. Зависимости результирующей силы F и потенциальной энергии
- 11. При некотором расстоянии r = r0 результирующая сила взаимодействия
- 12. Беспорядочное хаотическое движение молекул называется тепловым движением. Кинетическая энергия теплового движения растет с возрастанием температуры.
- 13. При низких температурах средняя кинетическая энергия молекулы
- 14. В твердых телах молекулы совершают беспорядочные колебания
- 15. В жидкостях средняя кинетическая энергия молекул близка
- 16. Согласно теории Я.И. Френкеля, молекулы жидкости, подобно
- 17. Таким образом, молекулы жидкости не привязаны к
- 18. Слайд 18
- 19. Переход молекулы жидкости из одного положения равновесия
- 20. С повышением температуры среднее время оседлой жизни
- 21. 2. Вязкость (внутреннее трение) жидкости. Формула
- 22. Рассмотрим два слоя жидкости, движущиеся с разными
- 23. Слайд 23
- 24. Исаак Ньютон показал, что сила трения между
- 25. Коэффициент η («эта») называется коэффициентом вязкости или
- 26. Коэффициент вязкости зависит, прежде всего, от природы
- 27. Слайд 27
- 28. Слайд 28
- 29. Для большинства жидкостей коэффициент вязкости при постоянной
- 30. Однако опыт показал, что для ряда жидкостей
- 31. Слайд 31
- 32. Такие жидкости называются «неньютоновскими». К ним относятся
- 33. Цельная кровь (суспензия эритроцитов в белковом растворе - плазме) является неньютоновской жидкостью вследствие агрегации эритроцитов.
- 34. 3. Способы измерения вязкости Для измерения
- 35. Капиллярные вискозиметрыа) Вискозиметр Уббелодеб) Вискозиметр Освальдав) Медицинский вискозиметр ВК-4
- 36. Вискозиметр крови «Антарес» ВКА-0801
- 37. 4. Механические свойства твердых телСилы притяжения и
- 38. Деформация - изменение формы или объема тела
- 39. Деформацию растяжения и сжатия можно охарактеризовать абсолютной
- 40. Отношение абсолютной деформации Δℓ к первоначальной длине
- 41. Если деформация упругая, а относительная деформация невелика,
- 42. k - коэффициент жесткости (упругости).Зависит от материала,
- 43. Физическая величина, равная отношению модуля силы упругости
- 44. Отношение механического напряжения к относительному удлинению (при
- 45. Модуль Юнга Е не зависит от формы
- 46. Посколькуто:где
- 47. Получили закон Гука.Другая форма записи закона Гука:σ = E.ε(Механическое напряжение прямо пропорционально модулю относительной деформации.)
- 48. Диаграмма растяжения
- 49. σпроп – предел пропорциональности (максимальное напряжение, при
- 50. Механические свойства полимеровПолимером называется органическое вещество, длинные
- 51. Слайд 51
- 52. Одна из основных особенностей полимеров состоит в
- 53. Эти виды внутреннего движения — смена конформаций,
- 54. Полимерам наряду с обычной упругой деформацией свойствен
- 55. Переход из высокоэластического состояния в стеклообразное, характеризующееся
- 56. Особенность полимеров состоит также в том, что
- 57. В какой-то мере процессы, происходящие в полимерах,
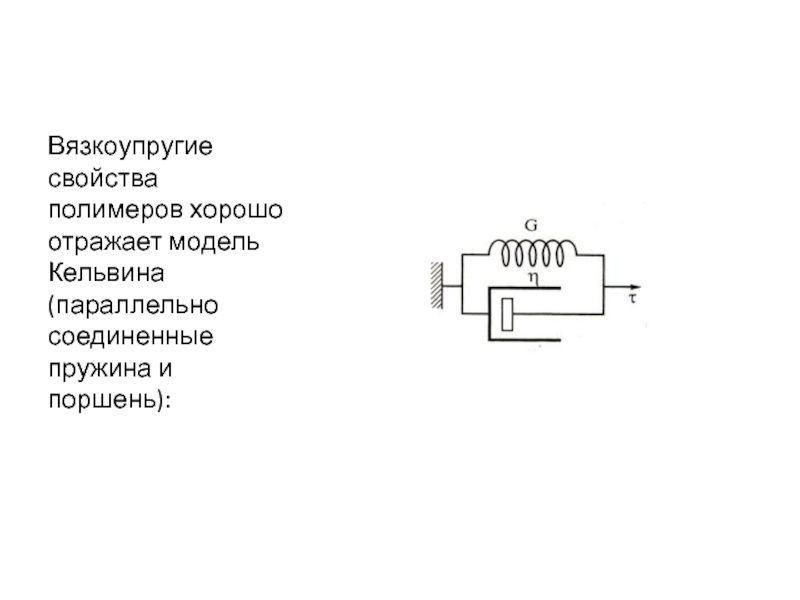
- 58. Упругие и вязкие свойства тел удобно моделировать.В
- 59. Вязкоупругие свойства моделируются системами, состоящими из различных комбинаций двух простых моделей: пружины и поршня.Модель Максвелла:
- 60. Вязкоупругие свойства полимеров хорошо отражает модель Кельвина (параллельно соединенные пружина и поршень):
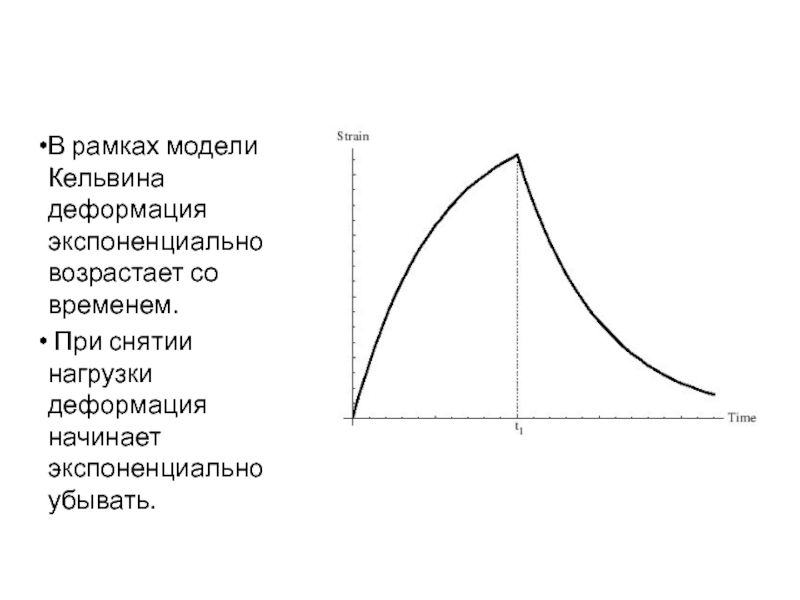
- 61. В рамках модели Кельвина деформация экспоненциально возрастает со временем. При снятии нагрузки деформация начинает экспоненциально убывать.
- 62. Моделирование механических свойств тел широко используется в
- 63. Скачать презентанцию
Механика (от греч. mechanike – искусство построения машин) - наука о механическом движении материальных тел (т. е. изменении с течением времени взаимного положения тел или их частей в пространстве) и взаимодействиях
Слайды и текст этой презентации
Слайд 1
ВОЕННО–МЕДИЦИНСКАЯ АКАДЕМИЯ
имени С.М. Кирова
Кафедра биологической и медицинской физики
ЛЕКЦИЯ № 3
по
дисциплине «Физика, математика»
I курса ФПВ, ФПиУГВ, спецфакультета
Слайд 2
Механика (от греч. mechanike – искусство построения машин) - наука
о механическом движении материальных тел (т. е. изменении с течением
времени взаимного положения тел или их частей в пространстве) и взаимодействиях между ними.
Слайд 3
МЕХАНИЧЕСКИЕ СВОЙСТВА материалов определяют их поведение под действием механической нагрузки.
Слайд 4
Большое значение для врача имеет механика жидкостей и газов -
наука, изучающая закономерности покоя и движения жидкостей и газов.
Слайд 5 1. Особенности структуры и молекулярного движения в жидкостях, газах и
твердых телах.
Основными агрегатными состояниями вещества считают газообразное, жидкое и твердое
состояния. Газы обладают сжимаемостью. Они способны заполнять весь объем сосуда, в котором находятся.
Твердые тела несжимаемы, сохраняют свою форму и размеры. Различают кристаллические и аморфные твердые тела. По своим механическим свойствам все тела делятся на упругие, пластичные и хрупкие.
Слайд 6
Жидкость - это агрегатное состояние вещества, промежуточное между твердым и
газообразным.
Одни свойства жидкостей роднят их с твердыми телами (наличие
определенного объема, относительная несжимаемость, ближний порядок молекул, плотность, наличие поверхности), другие – с газами (отсутствие определенной формы). При этом жидкости обладают и только им присущими свойствами, например, текучестью.
Слайд 7
Существование у вещества нескольких агрегатных состояний обусловлено различиями в тепловом
движении его молекул/атомов и в их взаимодействии.
Слайд 8
Основные положения молекулярно-кинетической теории (МКТ):
Все тела состоят из мельчайших частиц
– молекул, атомов или ионов. Эти частицы находятся в состоянии постоянного хаотического теплового движения.
Между молекулами действуют силы притяжения и силы отталкивания, имеющие электрическую природу.
Слайд 9
Силы, действующие между двумя молекулами, зависят от расстояния между ними.
Молекулы представляют собой сложные пространственные структуры, содержащие как положительные, так
и отрицательные заряды.Если расстояние между молекулами достаточно велико, то преобладают силы межмолекулярного притяжения. На малых расстояниях преобладают силы отталкивания.
Слайд 10
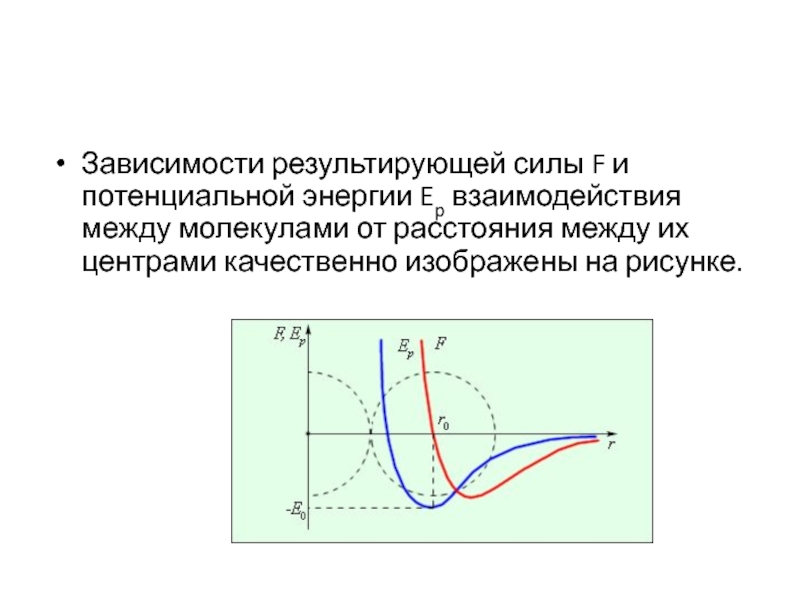
Зависимости результирующей силы F и потенциальной энергии Ep взаимодействия между
молекулами от расстояния между их центрами качественно изображены на рисунке.
Слайд 11
При некотором расстоянии r = r0 результирующая сила взаимодействия обращается в нуль.
Это расстояние условно можно принять за диаметр молекулы.
Потенциальная энергия
взаимодействия при r = r0 минимальна. Чтобы удалить друг от друга две молекулы, находящиеся на расстоянии r0, нужно сообщить им дополнительную энергию E0. Величина E0 называется глубиной потенциальной ямы, или энергией связи.
Слайд 12
Беспорядочное хаотическое движение молекул называется тепловым движением. Кинетическая энергия теплового
движения растет с возрастанием температуры.
Слайд 13
При низких температурах средняя кинетическая энергия молекулы может оказаться меньше
глубины потенциальной ямы E0. В этом случае молекулы конденсируются в
твердое вещество; при этом среднее расстояние между молекулами будет приблизительно равно r0.При повышении температуры средняя кинетическая энергия молекулы становится больше E0, молекулы разлетаются, и образуется газообразное вещество.
Слайд 14
В твердых телах молекулы совершают беспорядочные колебания около фиксированных центров
(положений равновесия). Эти центры могут быть расположены в пространстве нерегулярным
образом (аморфные тела) или образовывать упорядоченные объемные структуры (кристаллические тела).
Слайд 15
В жидкостях средняя кинетическая энергия молекул близка к глубине потенциальной
ямы.
Поэтому молекулы жидкости имеют значительно большую свободу для теплового
движения. 
Слайд 16
Согласно теории Я.И. Френкеля, молекулы жидкости, подобно частицам твердого тела,
колеблются около положений равновесия, однако эти положения равновесия не являются
постоянными.По истечении некоторого времени, называемого временем оседлой жизни (порядка 10-9 с), за которое совершается порядка 1000 колебаний, молекула скачком переходит в новое положение равновесия на расстояние, равное среднему расстоянию между молекулами.
Слайд 17
Таким образом, молекулы жидкости не привязаны к определенным центрам и
могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей.
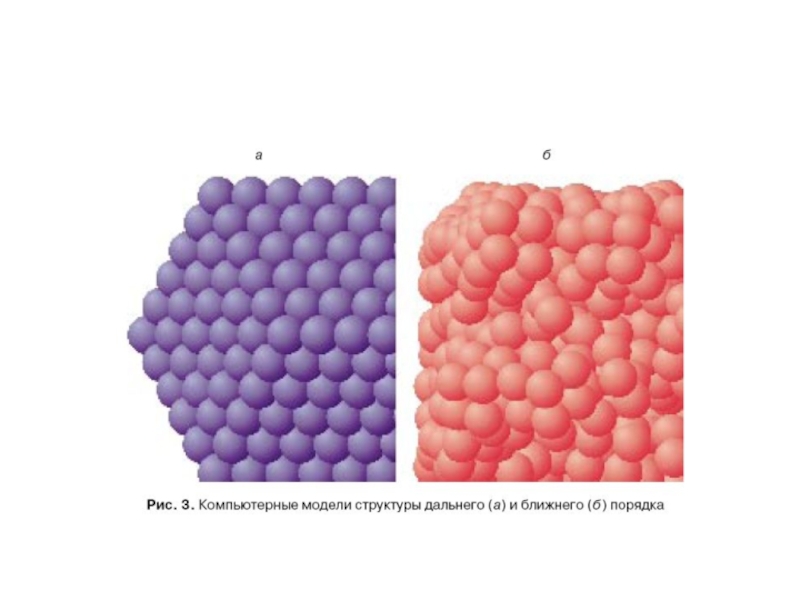
Близко
расположенные молекулы жидкости также могут образовывать упорядоченные структуры, содержащие несколько молекул. Это явление называется ближним порядком в отличие от дальнего порядка, характерного для кристаллических тел. 
Слайд 19
Переход молекулы жидкости из одного положения равновесия в другое является
переходом через потенциальный барьер высотой Е0.
Энергию для перехода через
потенциальный барьер молекула получает за счет энергии теплового движения соседних молекул. 
Слайд 20
С повышением температуры среднее время оседлой жизни молекул уменьшается, так
как увеличиваются средняя кинетическая энергия молекул и вероятность преодоления молекулами
потенциального барьера.Соответственно, увеличивается текучесть жидкости и уменьшается ее вязкость.
Слайд 21 2. Вязкость (внутреннее трение) жидкости. Формула Ньютона. Ньютоновские и неньютоновские
жидкости.
В реальных жидкостях всегда существуют силы трения.
В отличие
от твёрдых тел, где силы трения действуют между двумя разными телами, в жидкостях силы трения возникают внутри жидкости (между разными её слоями). Поэтому трение в жидкостях называют внутренним трением или вязкостью.
Слайд 22
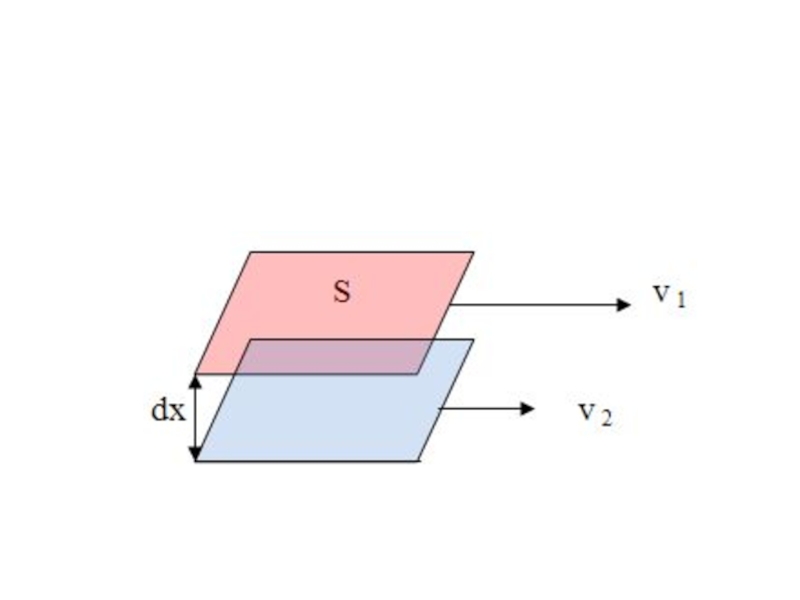
Рассмотрим два слоя жидкости, движущиеся с разными скоростями v1 и
v2.
Расстояние между слоями равно dх.
Выделим в каждом слое
площадку с площадью S.
Слайд 24
Исаак Ньютон показал, что сила трения между этими слоями равна:
Знак
„минус" показывает, что сила трения направлена навстречу движению.
Эта формула
носит название формулы Ньютона.
Слайд 25
Коэффициент η («эта») называется коэффициентом вязкости или динамической вязкостью (реже
говорят «коэффициент внутреннего трения»).
Размерность коэффициента вязкости - Па.с (паскаль-секунда).
В
старой литературе можно встретить внесистемную единицу „пуаз" (П). 1 Па.с = 10 П
Слайд 26
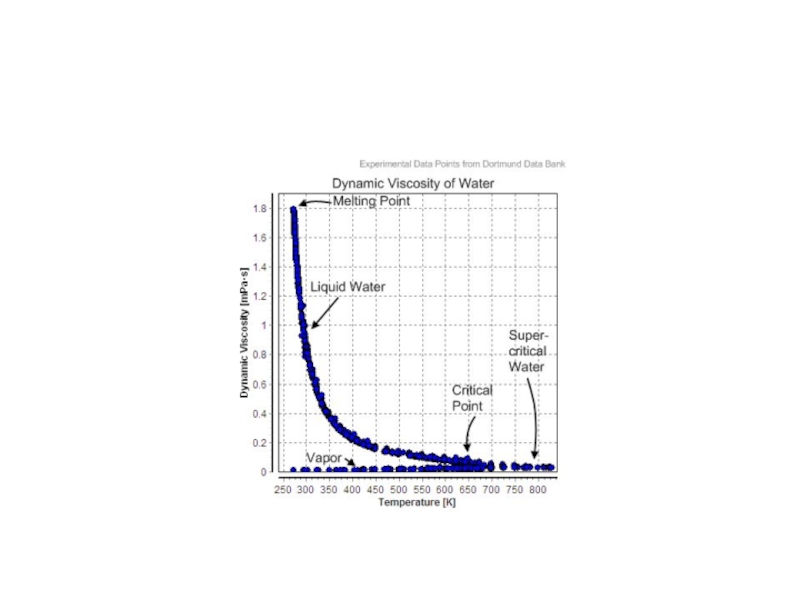
Коэффициент вязкости зависит, прежде всего, от природы жидкости (например, у
воды вязкость относительно мала, у масла много больше).
Кроме того,
он сильно зависит от температуры. С ростом температуры вязкость сильно уменьшается по экспоненциальному закону.
Слайд 29
Для большинства жидкостей коэффициент вязкости при постоянной температуре есть постоянная
величина, зависящая только от природы жидкости и не зависящая от
её скорости (точнее, от градиента скорости). Такие жидкости принято называть „ньютоновскими", то есть строго подчиняющимися закону Ньютона.
Слайд 30
Однако опыт показал, что для ряда жидкостей η≠const.
При малых
градиентах скорости (что чаще всего бывает, когда сама скорость движения
жидкости мала) вязкость относительно велика, но с ростом градиента скорости вязкость уменьшается, приближаясь к некоторому, сравнительно малому постоянному значению.
Слайд 32
Такие жидкости называются «неньютоновскими».
К ним относятся структурированные дисперсные системы
(суспензии, эмульсии), растворы и расплавы некоторых полимеров, многие органические жидкости
и др.При прочих равных условиях вязкость таких жидкостей значительно больше, чем у ньютоновских жидкостей.
Это связано с тем, что благодаря сцеплению молекул или частиц в неньютоновской жидкости образуются пространственные структуры, на разрушение которых затрачивается дополнительная энергия.
Слайд 33
Цельная кровь (суспензия эритроцитов в белковом растворе - плазме) является
неньютоновской жидкостью вследствие агрегации эритроцитов.
Слайд 34
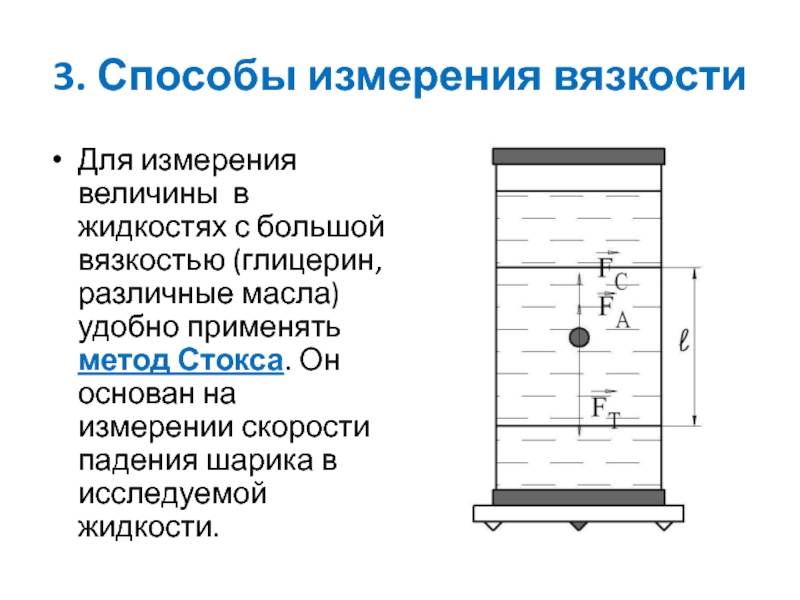
3. Способы измерения вязкости
Для измерения величины в жидкостях с большой
вязкостью (глицерин, различные масла) удобно применять метод Стокса. Он основан
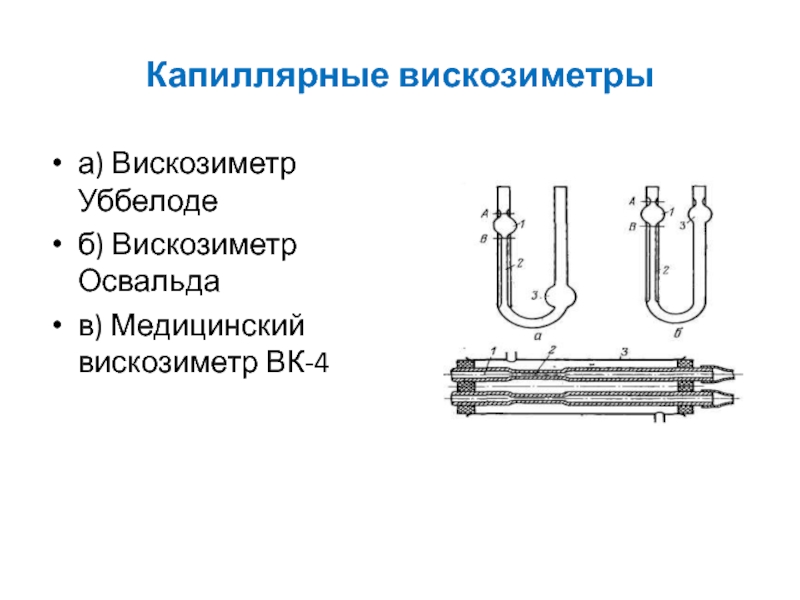
на измерении скорости падения шарика в исследуемой жидкости.
Слайд 35Капиллярные вискозиметры
а) Вискозиметр Уббелоде
б) Вискозиметр Освальда
в) Медицинский вискозиметр ВК-4
Слайд 374. Механические свойства твердых тел
Силы притяжения и отталкивания обуславливают механическую
прочность твердых тел. т. е. их способность противодействовать изменению формы
и объема.Растяжению тел препятствуют силы межатомного притяжения, а сжатию - силы отталкивания.
Слайд 38
Деформация - изменение формы или объема тела под действием внешних
сил.
Деформация может быть упругая (после прекращения воздействия тело полностью
восстанавливает первоначальную форму и размеры) или неупругая (после прекращения воздействия тело не восстанавливает первоначальную форму или размеры). 
Слайд 39
Деформацию растяжения и сжатия можно охарактеризовать абсолютной деформацией Δℓ, равной
разности длин образца после растяжения ℓ и до него ℓ0:
Δℓ = ℓ – ℓ0
Слайд 40
Отношение абсолютной деформации Δℓ к первоначальной длине образца ℓo называют
относительной деформацией:
ε = Δℓ / ℓo
Слайд 41
Если деформация упругая, а относительная деформация невелика, то выполняется экспериментально
установленный
закон Гука:
Сила упругости прямо пропорциональна абсолютной
деформации.Fупр. = -k Δℓ
Слайд 42
k - коэффициент жесткости (упругости).
Зависит от материала, формы и размеров
тела.
Единица коэффициента упругости в СИ:
1 Н/м .
Слайд 43
Физическая величина, равная отношению модуля силы упругости Fупр., возникающей при
деформации, к площади сечения S образца, перпендикулярного вектору силы Fупр.,
называется механическим напряжением:σ = Fупр./S
Единица измерения: 1 Па (паскаль) = 1Н/м2.
Слайд 44
Отношение механического напряжения к относительному удлинению (при малых упругих деформациях
растяжения и сжатия) называется модулем упругости Е (модулем Юнга):
E =
σ | ε 
Слайд 45
Модуль Юнга Е не зависит от формы и размеров предмета,
изготовленных из данного материала.
Размерность модуля Юнга - Па.
Модуль Юнга показывает, какое надо создать механическое напряжение, чтобы деформировать тело в 2 раза (Δℓ / ℓo= 1).
Слайд 47
Получили закон Гука.
Другая форма записи закона Гука:
σ = E.ε
(Механическое напряжение
прямо пропорционально модулю относительной деформации.)
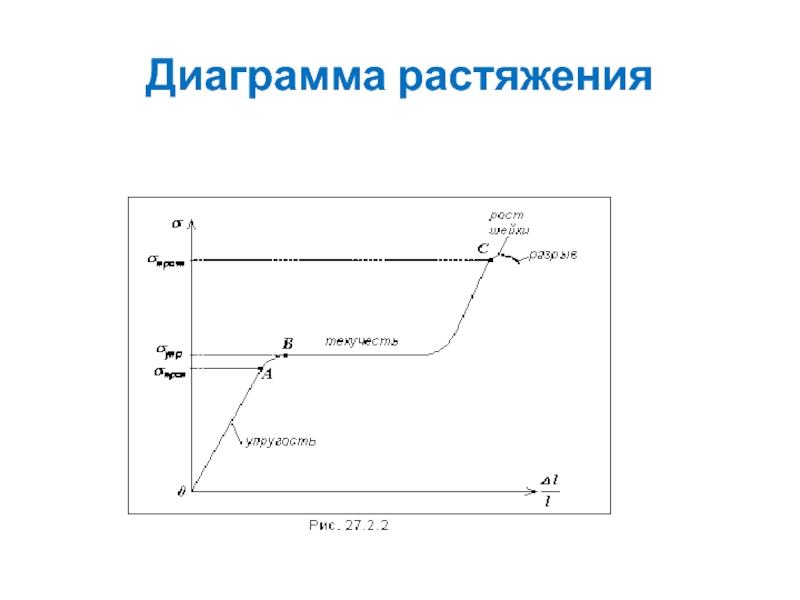
Слайд 49
σпроп – предел пропорциональности (максимальное напряжение, при котором деформация еще
остается упругой и выполняется закон Гука).
σупр – предел упругости (максимальное
напряжение, при котором еще не возникают заметные остаточные деформации, и материал еще сохраняет упругие свойства).σт – предел текучести (напряжение, при котором материал «течет»).
σпрочн – предел прочности (наибольшее напряжение, которое способен выдержать образец без разрушения).
Слайд 50Механические свойства полимеров
Полимером называется органическое вещество, длинные молекулы которого построены
из одинаковых многократно повторяющихся звеньев — мономеров.
Механические свойства полимеров резко
отличаются от кристаллических мономеров (например, стали).Сталь разрывается уже при растяжении на 0,3%, мягкие резины можно растягивать до 300%.
Слайд 52
Одна из основных особенностей полимеров состоит в том, что отдельные
отрезки цепей (сегменты) могут перемещаться путем поворота вокруг химической связи
и изменения угла.Такое смещение, в отличие от растяжения связей при упругой деформации истинно твердых тел, не требует большой энергии и происходит при невысокой температуре.
Слайд 53
Эти виды внутреннего движения — смена конформаций, несвойственные другим твердым
телам, придают полимерам сходство с жидкостями.
В то же время
большая длина искривленных и спиралеобразных молекул, их ветвление и взаимная сшивка затрудняют смещение, вследствие чего полимер приобретает свойства твердого тела.
Слайд 54
Полимерам наряду с обычной упругой деформацией свойствен ее оригинальный вид
— высокоэластическая деформация, которая становится преобладающей при повышении температуры.
Например,
мягкие резины можно растягивать до 300%, тогда как сталь разрывается уже при растяжении на 0,3%.
Слайд 55
Переход из высокоэластического состояния в стеклообразное, характеризующееся лишь упругой деформацией,
называется стеклованием.
Ниже температуры стеклования Тст состояние полимера твердое, стекловидное,
высокоупругое, выше—эластическое.
Слайд 56
Особенность полимеров состоит также в том, что их прочностные свойства
зависят от времени, т. е. предельная деформация устанавливается не сразу
после приложения нагрузки.Такая замедленная реакция их на механические напряжения объясняется инерционностью процесса смены конформаций.
Слайд 57
В какой-то мере процессы, происходящие в полимерах, напоминают течение вязкой
жидкости.
Сочетание вязкого течения и высокой эластичности позволяет называть деформацию,
характерную для полимеров, вязкоупругой.
Слайд 58
Упругие и вязкие свойства тел удобно моделировать.
В качестве модели упругого
тела (упругой деформации) используют пружину, малая деформация которой соответствует закону
Гука.Моделью вязкого тела является поршень с отверстиями, движущийся в цилиндре с вязкой жидкостью.
Слайд 59
Вязкоупругие свойства моделируются системами, состоящими из различных комбинаций двух простых
моделей: пружины и поршня.
Модель Максвелла:
Слайд 60
Вязкоупругие свойства полимеров хорошо отражает модель Кельвина (параллельно соединенные пружина
и поршень):
Слайд 61
В рамках модели Кельвина деформация экспоненциально возрастает со временем.
При снятии нагрузки деформация начинает экспоненциально убывать.
Слайд 62
Моделирование механических свойств тел широко используется в реологии.
Реология – это
раздел физики, изучающий деформацию и текучесть вещества.
Биореология исследует течение
разнообразных биологических жидкостей (например, крови, синовиальной, плевральной и др.), деформации различных тканей (мышц, костей, кровеносных сосудов) у человека и животных.
