Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
19 Геометрическое место точек. Окружность и круг
Содержание
- 1. 19 Геометрическое место точек. Окружность и круг
- 2. Геометрическим местом точек (ГМТ) называют множество всех
- 3. Геометрическим местом точек (ГМТ) называют множество всех
- 4. Какое множество точек можно назвать ГМТ?Каждая точка
- 5. Укажите фигуру, все точки которой и только они обладают следующими свойствами:Принадлежит одновременно двум данным пересекающимся прямым
- 6. Укажите фигуру, все точки которой и только
- 7. Укажите фигуру, все точки которой и только
- 8. Укажите фигуру, все точки которой и только они обладают следующими свойствами:Одновременно принадлежит двум сторонам данного треугольника
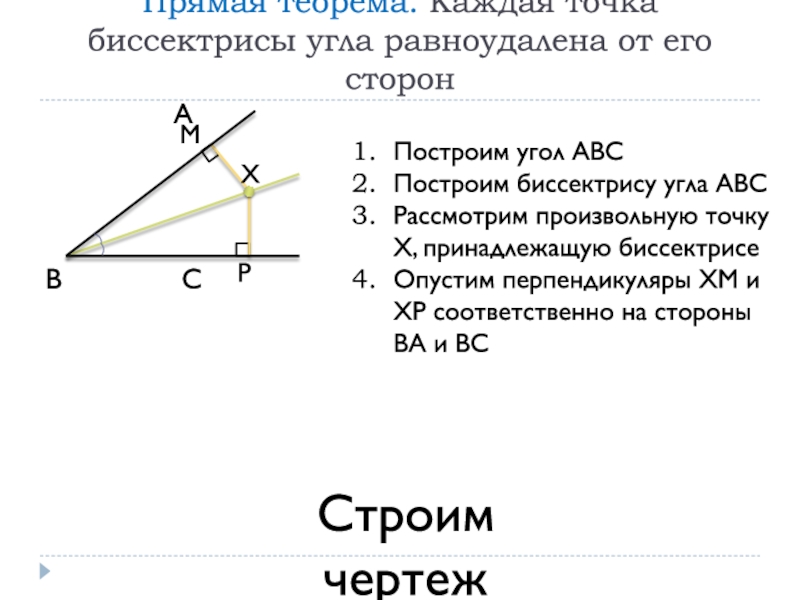
- 9. Прямая теорема. Каждая точка биссектрисы угла равноудалена от его сторонПостроим угол АВСПостроим биссектрису угла АВССтроим чертежАВС
- 10. Прямая теорема. Каждая точка биссектрисы угла равноудалена
- 11. А В
- 12. А В
- 13. Прямая теорема. Каждая точка биссектрисы угла равноудалена
- 14. Прямая теорема. Каждая точка биссектрисы угла равноудалена
- 15. Прямая теорема. Каждая точка биссектрисы угла равноудалена
- 16. Прямая теорема. Каждая точка биссектрисы угла равноудалена
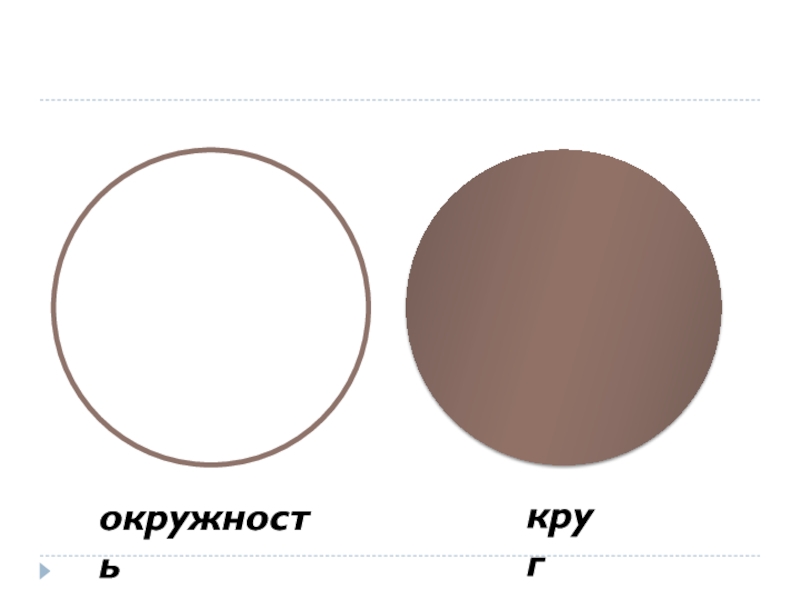
- 17. окружностькруг
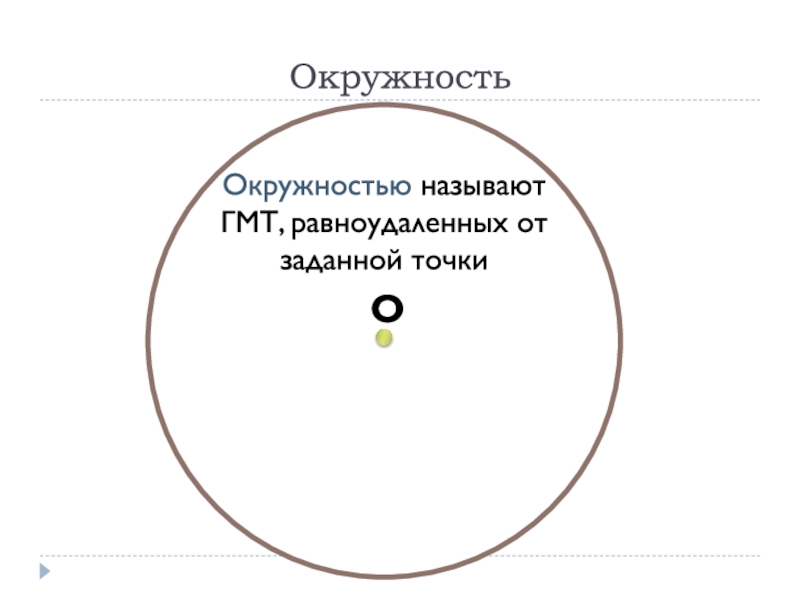
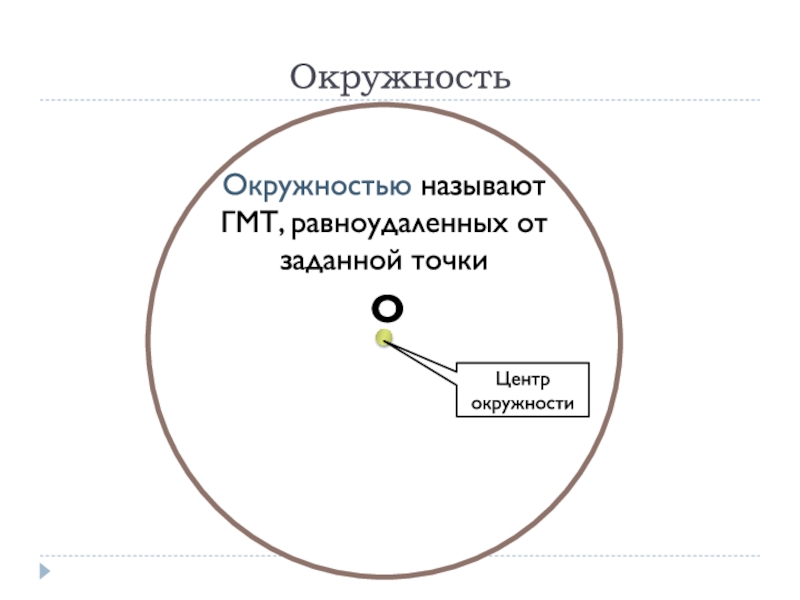
- 18. Окружностью называют ГМТ, равноудаленных от заданной точкиОкружность
- 19. ОкружностьОкружностью называют ГМТ, равноудаленных от заданной точкиЦентр окружности
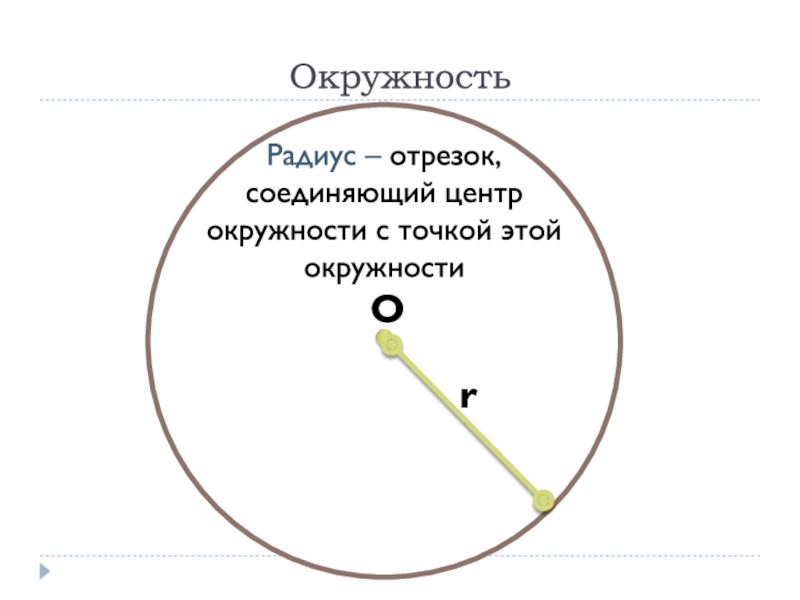
- 20. ОкружностьРадиус – отрезок, соединяющий центр окружности с точкой этой окружностиr
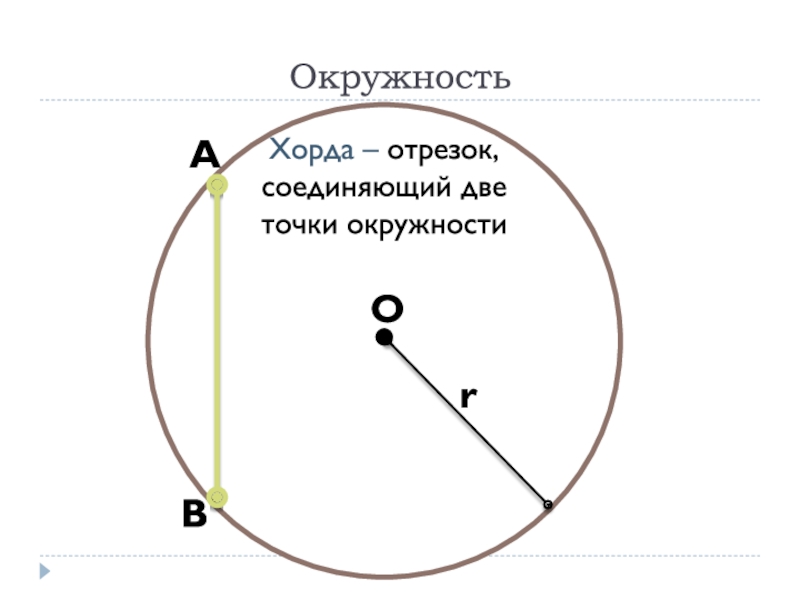
- 21. ОкружностьХорда – отрезок, соединяющий две точки окружностиОrАВ
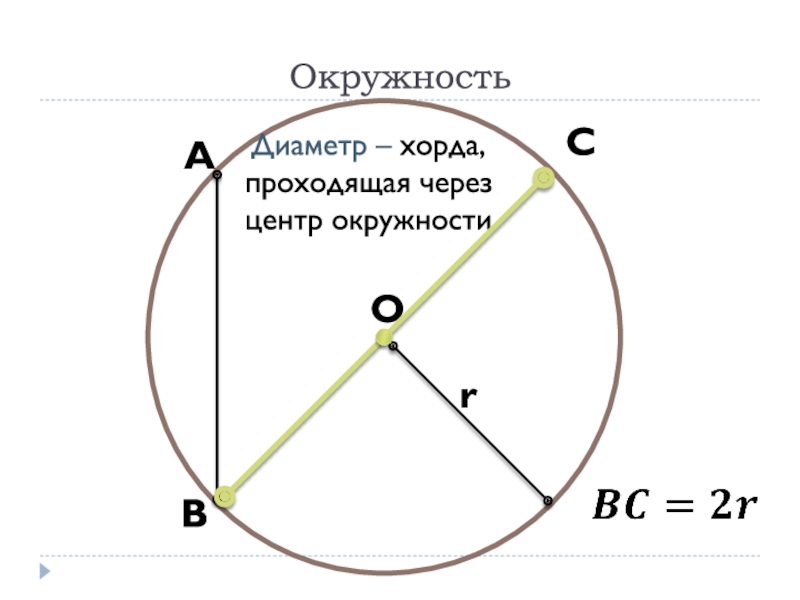
- 22. Диаметр – хорда, проходящая через центр окружностиОкружностьОrАВС
- 23. Кругом называют ГМТ, расстояние от которых до заданной точки не больше данного положительного числа
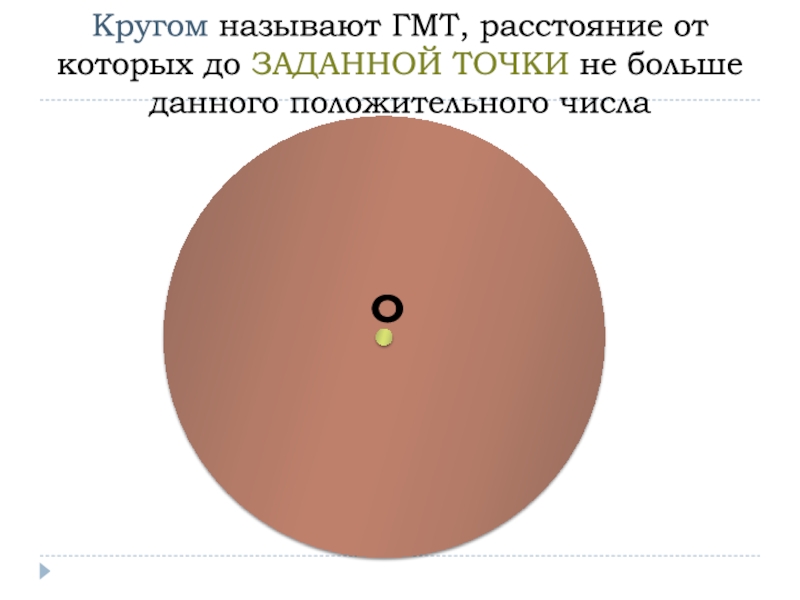
- 24. Кругом называют ГМТ, расстояние от которых до ЗАДАННОЙ ТОЧКИ не больше данного положительного числа
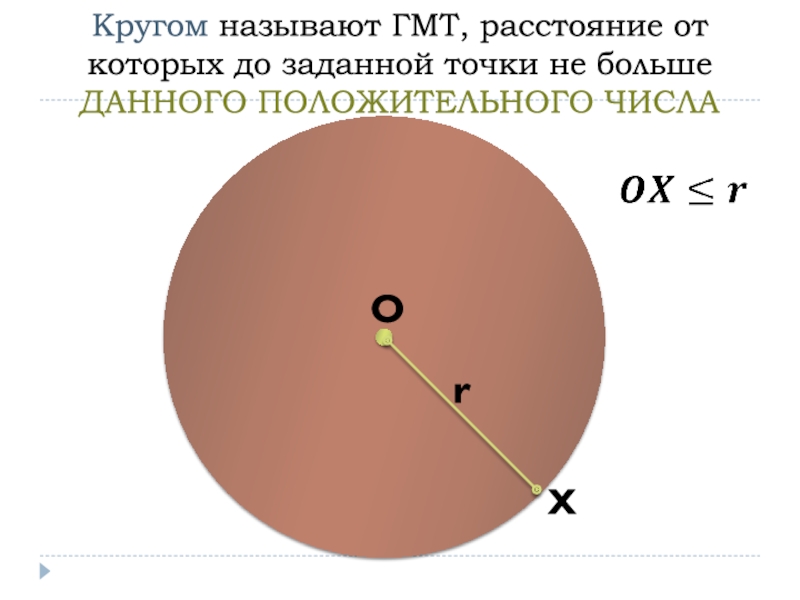
- 25. Кругом называют ГМТ, расстояние от которых до заданной точки не больше ДАННОГО ПОЛОЖИТЕЛЬНОГО ЧИСЛА rХ
- 26. Кругом называют ГМТ, расстояние от которых до заданной точки не больше данного положительного числа rХ
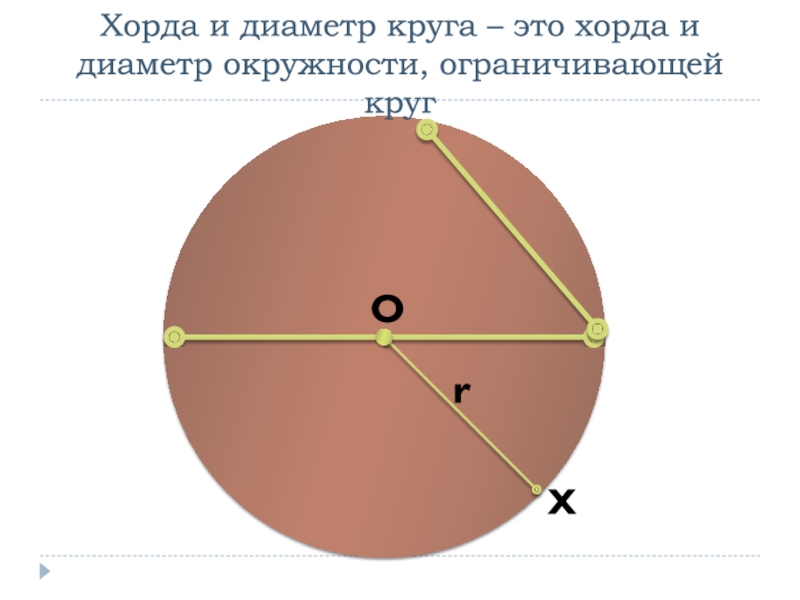
- 27. ОХорда и диаметр круга – это хорда и диаметр окружности, ограничивающей кругrХ
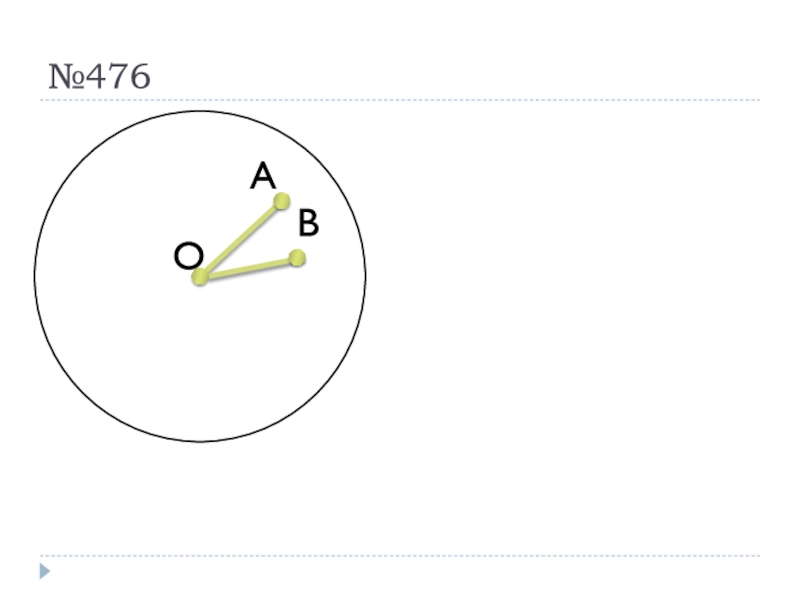
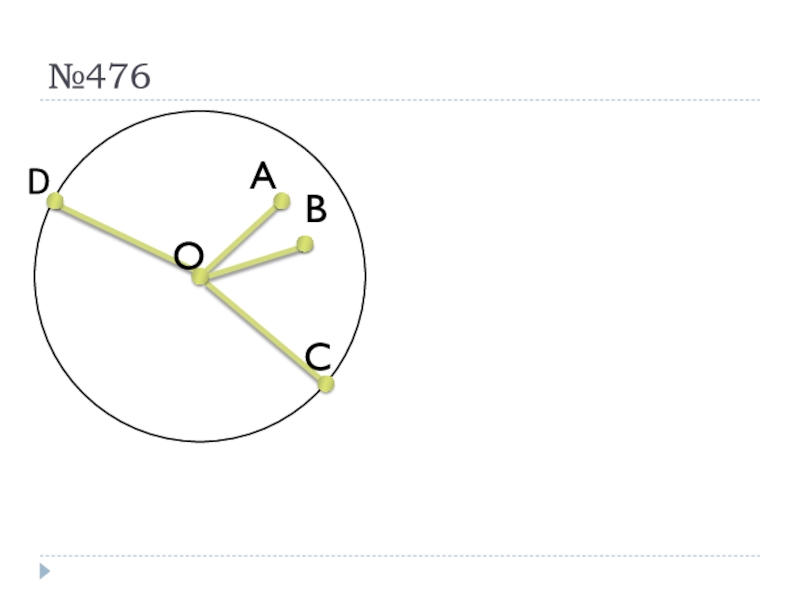
- 28. №476
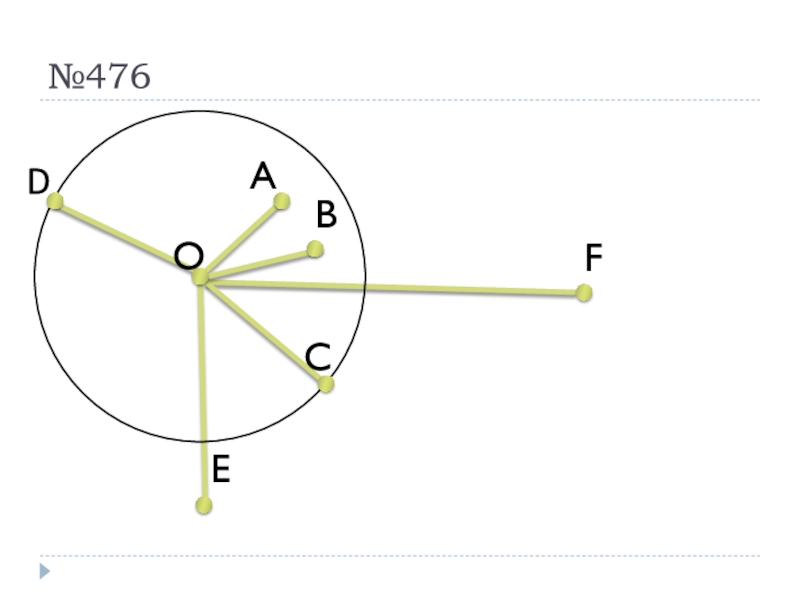
- 29. №476D
- 30. №476D
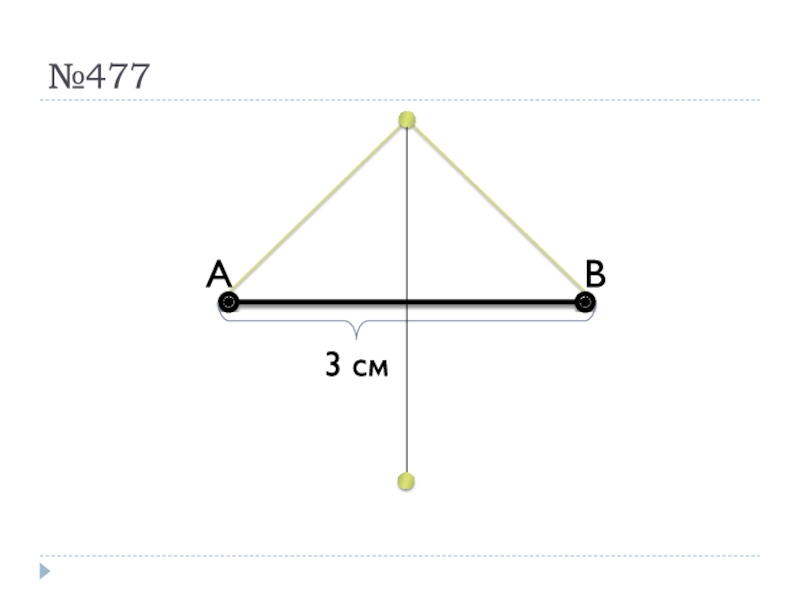
- 31. №477
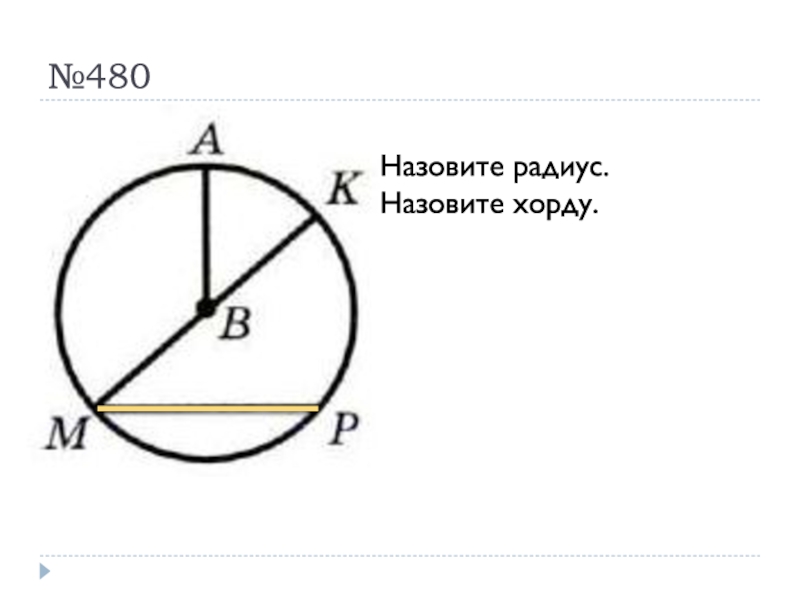
- 32. №480Назовите радиус.
- 33. №480Назовите радиус.Назовите хорду.
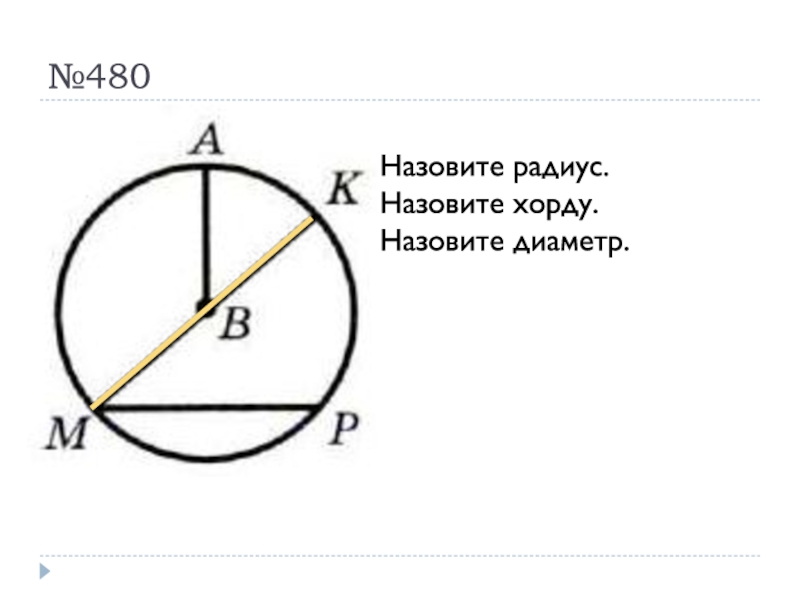
- 34. №480Назовите радиус.Назовите хорду.Назовите диаметр.
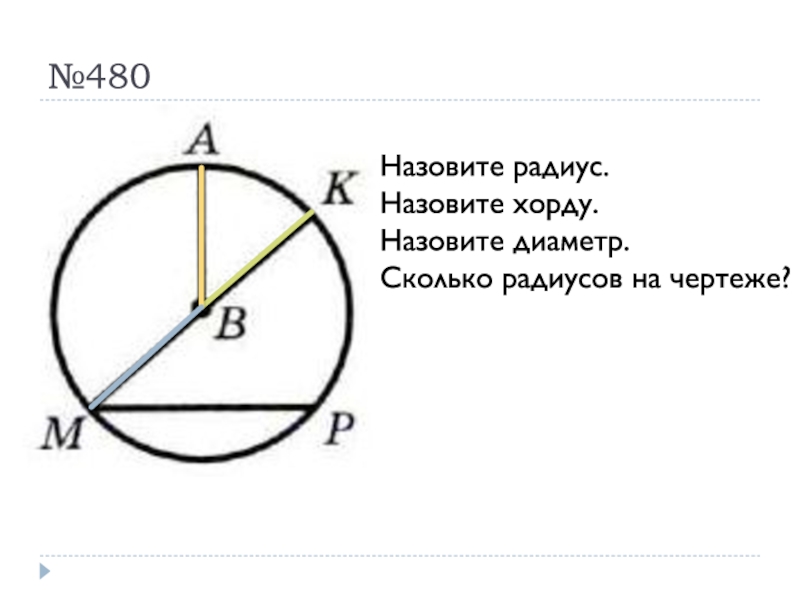
- 35. №480Назовите радиус.Назовите хорду.Назовите диаметр.Сколько радиусов на чертеже?
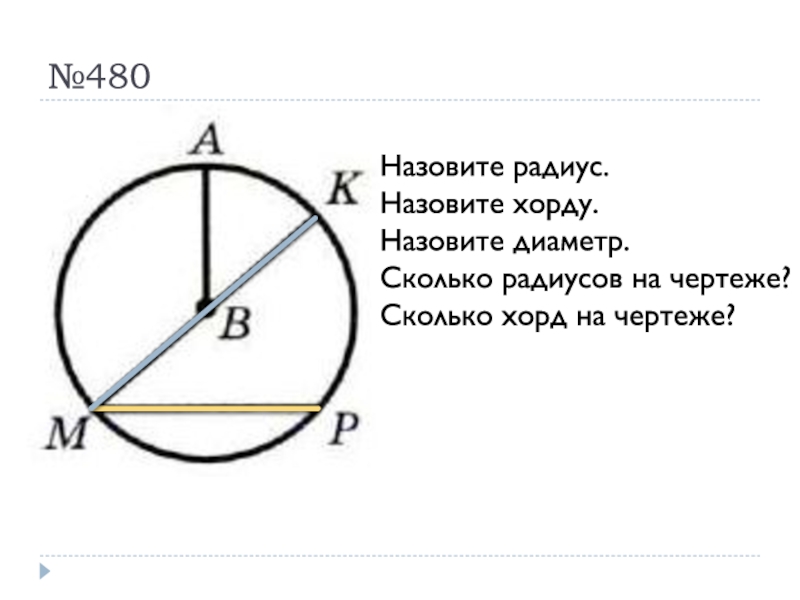
- 36. №480Назовите радиус.Назовите хорду.Назовите диаметр.Сколько радиусов на чертеже?Сколько хорд на чертеже?
- 37. №481Дано: окружность, О – центр окружностиО
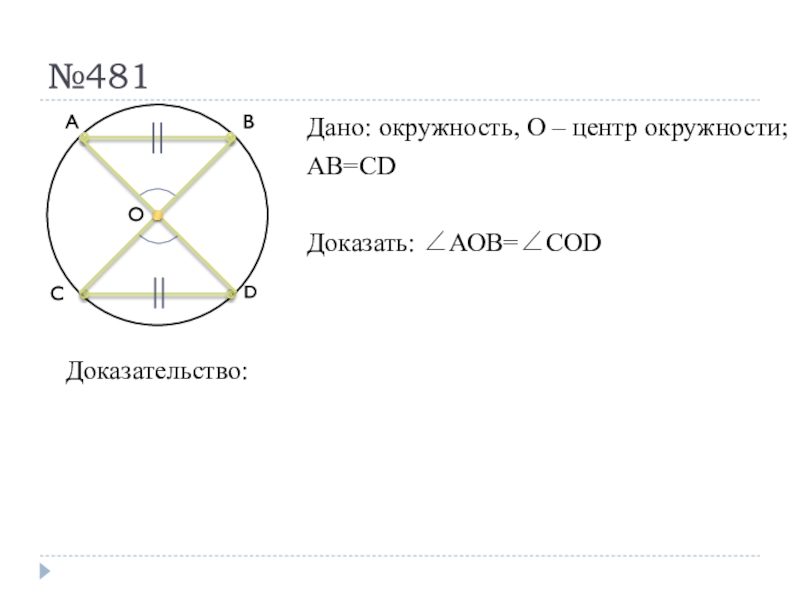
- 38. №481Дано: окружность, О – центр окружности;АВ=СDДоказать: АОВ=СODОАDСВДоказательство:
- 39. №481Дано: окружность, О – центр окружности;АВ=СDДоказать: АОВ=СODОАDСВДоказательство:Рассмотрим
- 40. №483Дано: окружность, О – центр окружностиАВ=СD –
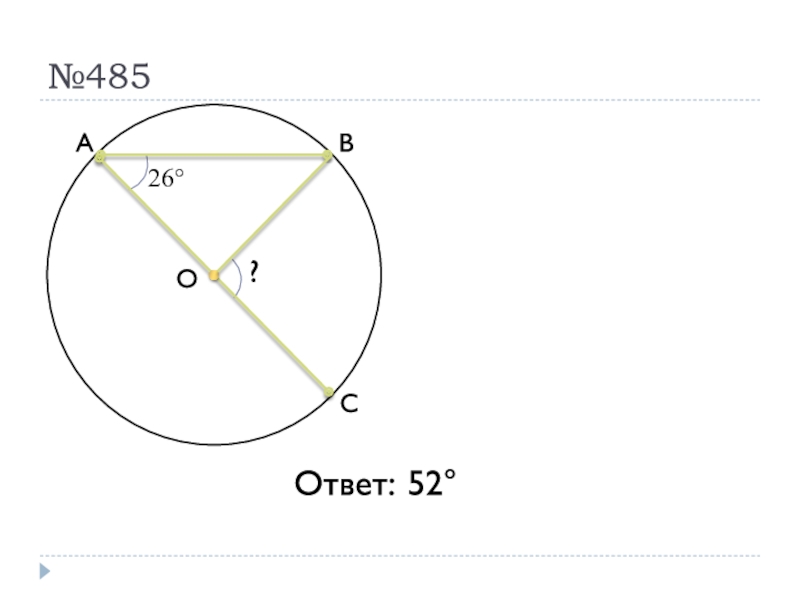
- 41. №485ОАСВ26° ?Ответ: 52°
- 42. №487ОАВС? Дано: окружность, О – центрАВ –
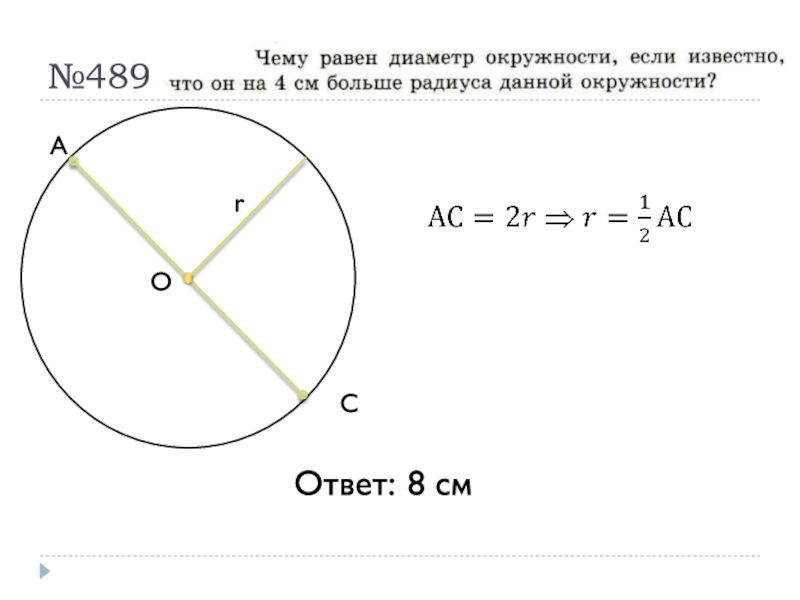
- 43. №489СОАrОтвет: 8 см
- 44. Самостоятельная работа (выполнить в тетради для ДЗ
- 45. Домашнее задание§19, вопросы 1-14 (устно)№482, №484,№488
- 46. Скачать презентанцию
Геометрическим местом точек (ГМТ) называют множество всех точек, обладающих определенным свойством.Все точки одновременно принадлежат лучам АВ и ВАИскомым ГМТ является отрезок АВАВ
Слайды и текст этой презентации
Слайд 1§19 Геометрическое место точек. Окружность и круг
Сделайте конспект презентации в
рабочую тетрадь
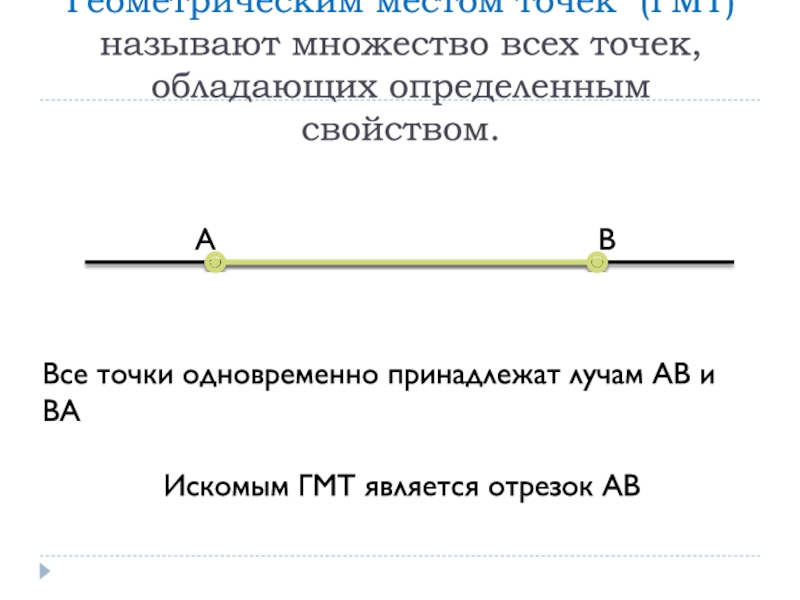
Слайд 2Геометрическим местом точек (ГМТ) называют множество всех точек, обладающих определенным
свойством.
Все точки одновременно принадлежат лучам АВ и ВА
Искомым ГМТ является
отрезок АВА
В
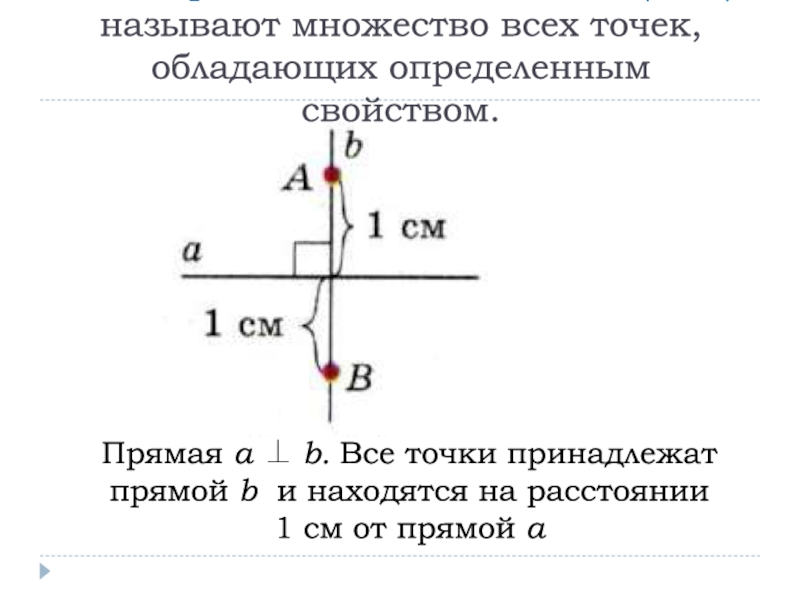
Слайд 3Геометрическим местом точек (ГМТ) называют множество всех точек, обладающих определенным
свойством.
Прямая а b. Все точки принадлежат прямой b и
находятся на расстоянии 1 см от прямой а
Слайд 4Какое множество точек можно назвать ГМТ?
Каждая точка данного множества обладает
заданным свойством;
Если точка обладает заданным свойством, то она принадлежит данному
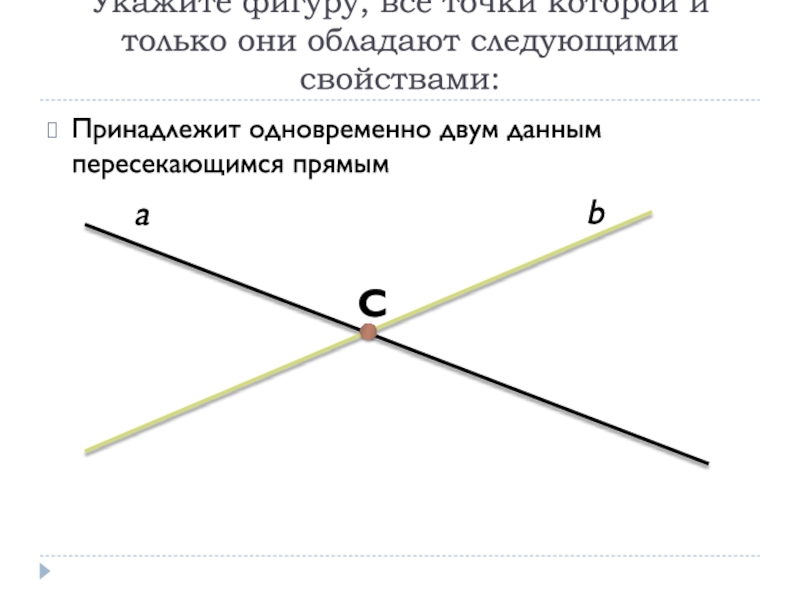
множеству
Слайд 5Укажите фигуру, все точки которой и только они обладают следующими
свойствами:
Принадлежит одновременно двум данным пересекающимся прямым
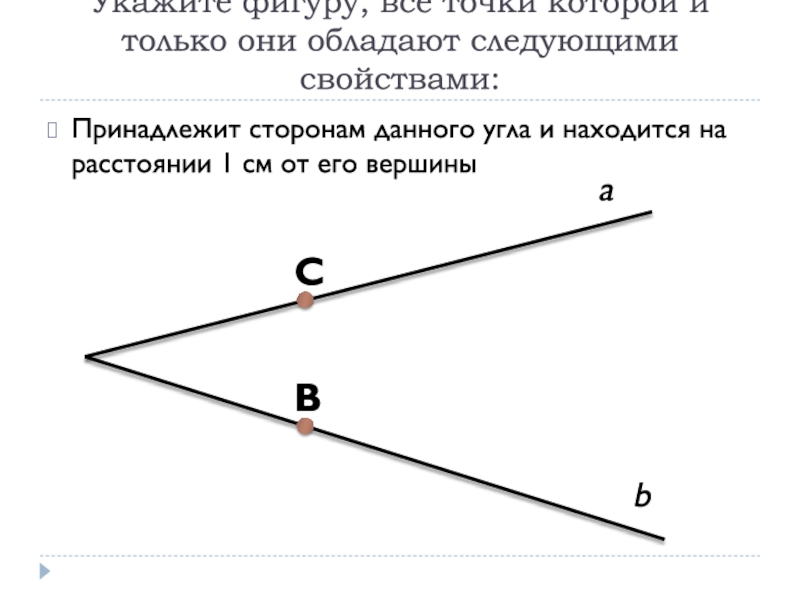
Слайд 6Укажите фигуру, все точки которой и только они обладают следующими
свойствами:
Принадлежит сторонам данного угла и находится на расстоянии 1 см
от его вершины
Слайд 7Укажите фигуру, все точки которой и только они обладают следующими
свойствами:
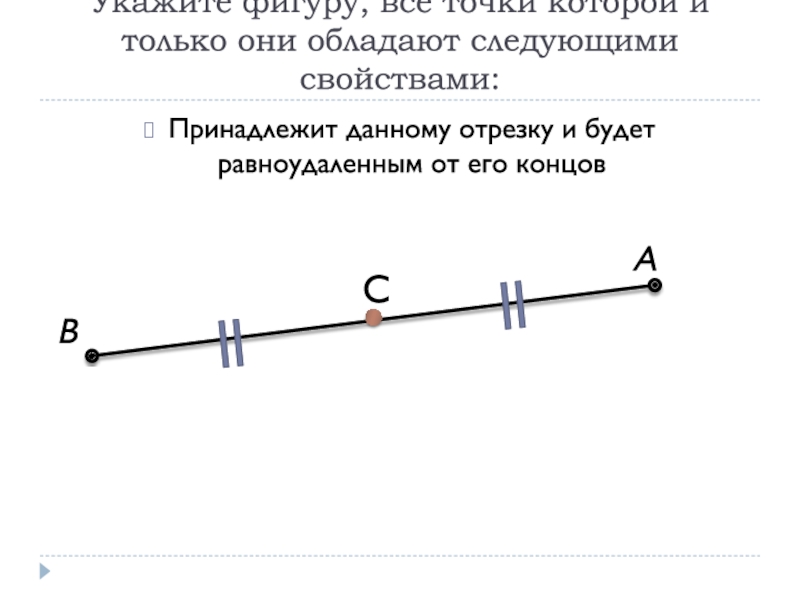
Принадлежит данному отрезку и будет равноудаленным от его концов
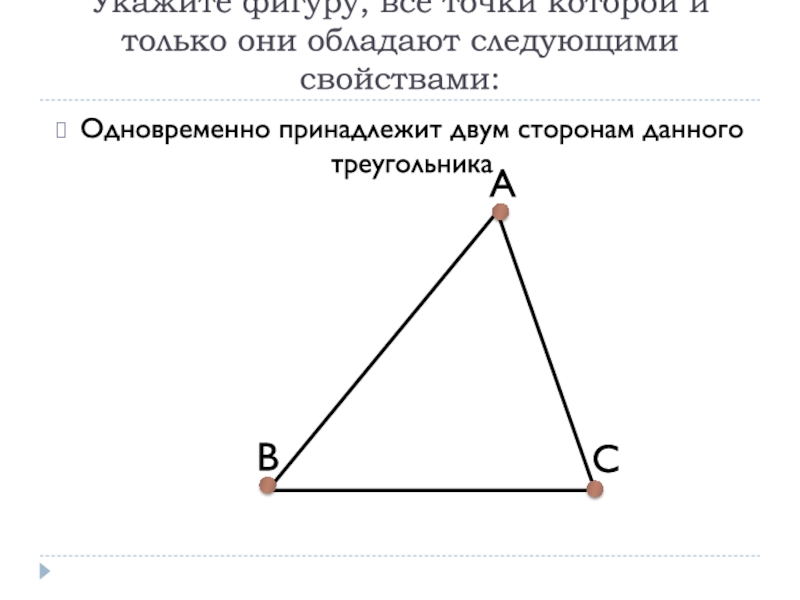
Слайд 8Укажите фигуру, все точки которой и только они обладают следующими
свойствами:
Одновременно принадлежит двум сторонам данного треугольника
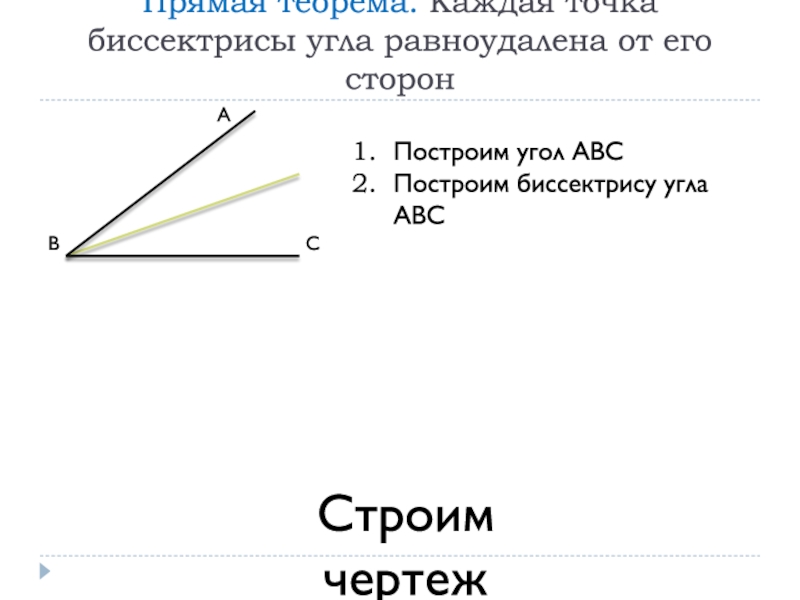
Слайд 9Прямая теорема. Каждая точка биссектрисы угла равноудалена от его сторон
Построим
угол АВС
Построим биссектрису угла АВС
Строим чертеж
А
В
С
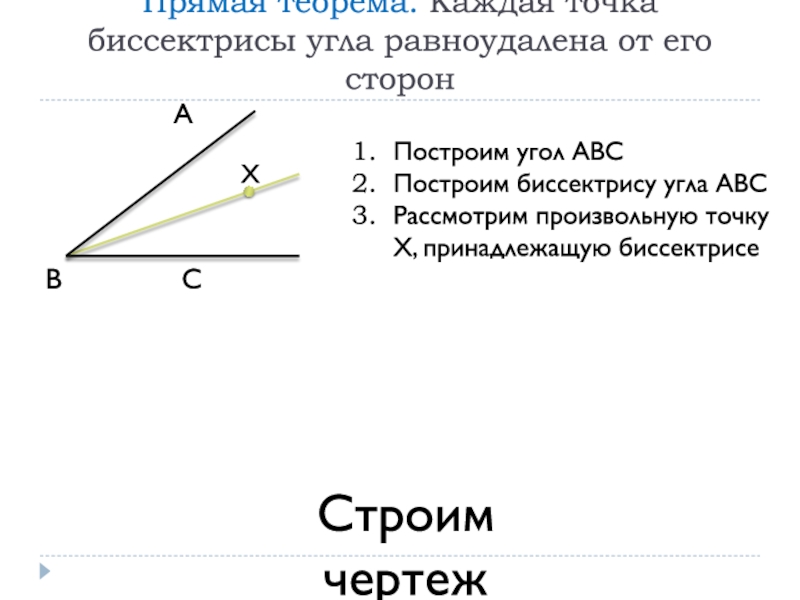
Слайд 10Прямая теорема. Каждая точка биссектрисы угла равноудалена от его сторон
А
В С
Х
Построим угол АВС
Построим
биссектрису угла АВСРассмотрим произвольную точку Х, принадлежащую биссектрисе
Строим чертеж
Слайд 11 А
В С
Прямая теорема.
Каждая точка биссектрисы угла равноудалена от его сторон
Х
Построим угол АВС
Построим
биссектрису угла АВСРассмотрим произвольную точку Х, принадлежащую биссектрисе
Опустим перпендикуляры ХМ и ХР соответственно на стороны ВА и ВС
М
Р
Строим чертеж
Слайд 13Прямая теорема. Каждая точка биссектрисы угла равноудалена от его сторон
А
В С
Х
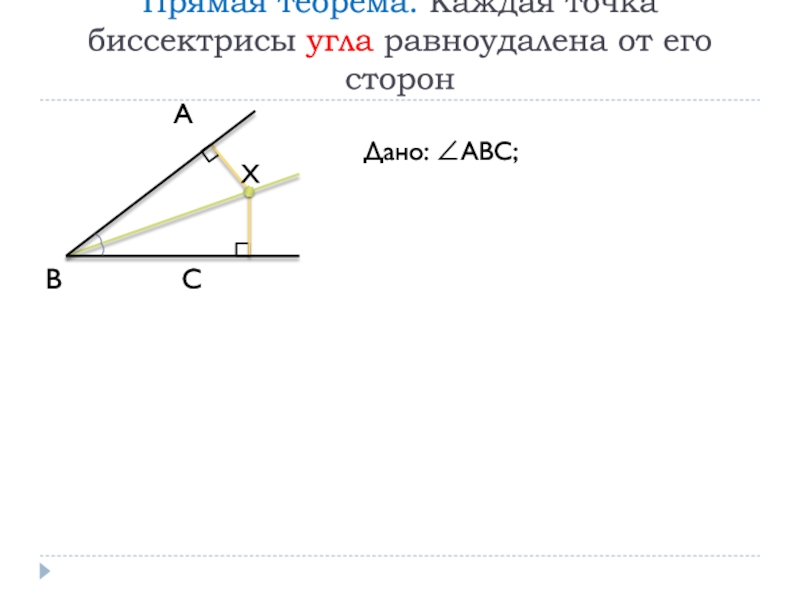
Дано: АВС; ВХ
– биссектриса М
Р
Слайд 14Прямая теорема. Каждая точка биссектрисы угла равноудалена от его сторон
А
В С
Х
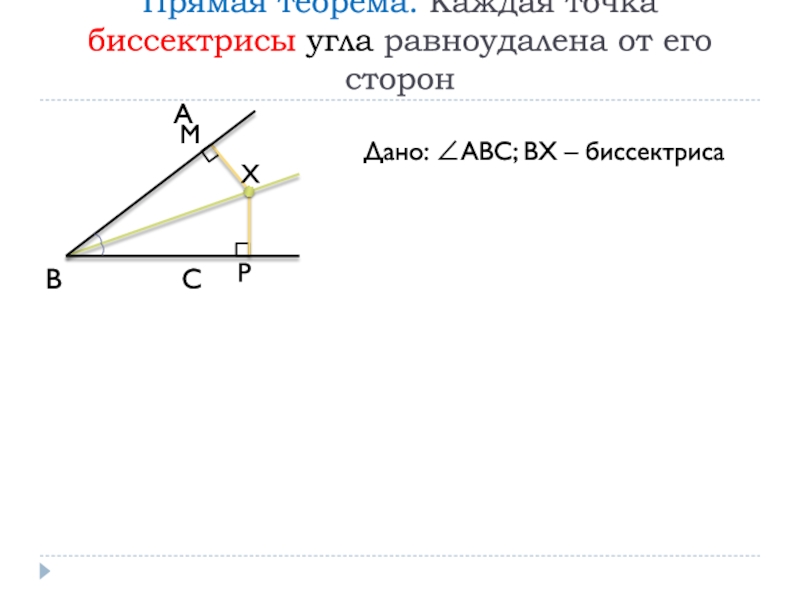
Дано: АВС; ВХ
– биссектрисаДоказать: ХМ=ХР
М
Р
Доказательство:
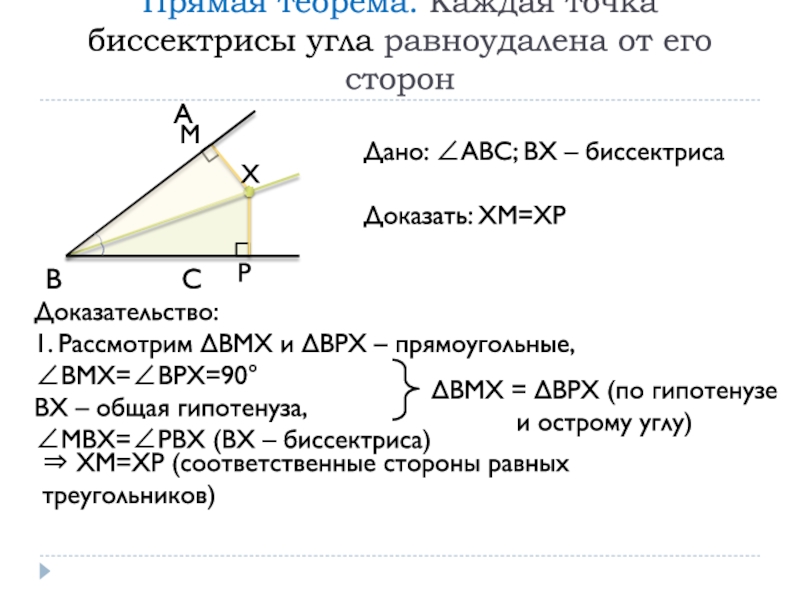
Слайд 15Прямая теорема. Каждая точка биссектрисы угла равноудалена от его сторон
А
В С
Х
Дано: АВС; ВХ
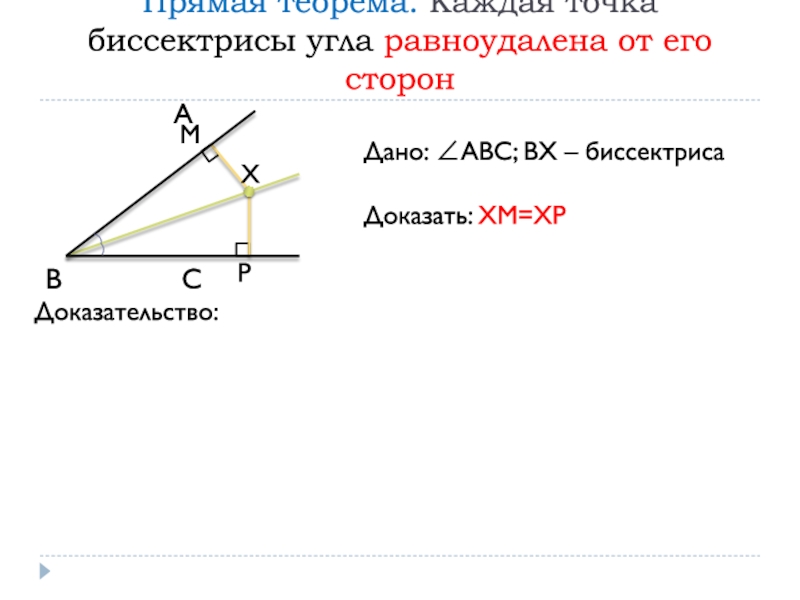
– биссектрисаДоказать: ХМ=ХР
М
Р
Доказательство:
1. Рассмотрим ВМХ и ВРХ – прямоугольные, ВМХ=ВРХ=90°
ВХ – общая гипотенуза,
МВХ=РВХ (ВХ – биссектриса)
ВМХ = ВРХ (по гипотенузе и острому углу)
ХМ=ХР (соответственные стороны равных треугольников)
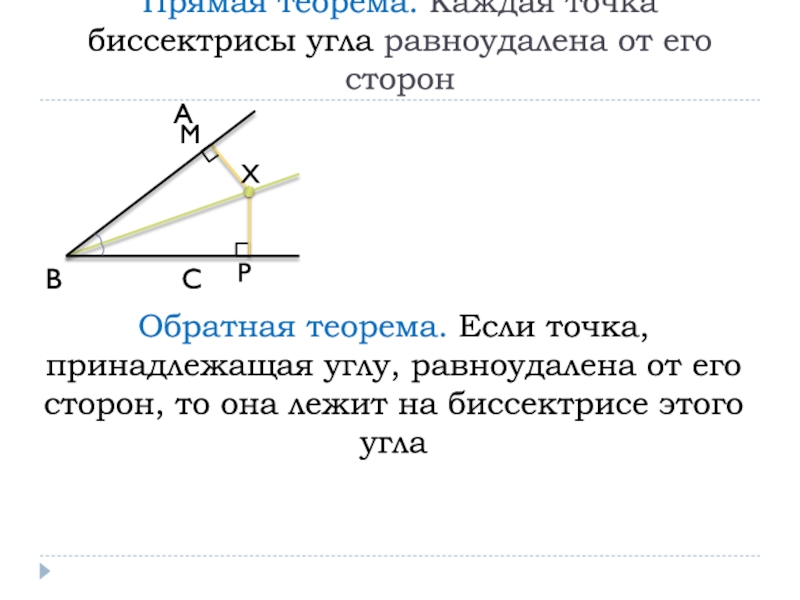
Слайд 16Прямая теорема. Каждая точка биссектрисы угла равноудалена от его сторон
А
В С
Х
М
Р
Обратная теорема. Если
точка, принадлежащая углу, равноудалена от его сторон, то она лежит на биссектрисе этого угла
Слайд 23Кругом называют ГМТ, расстояние от которых до заданной точки не
больше данного положительного числа
Слайд 24Кругом называют ГМТ, расстояние от которых до ЗАДАННОЙ ТОЧКИ не
больше данного положительного числа
Слайд 25Кругом называют ГМТ, расстояние от которых до заданной точки не
больше ДАННОГО ПОЛОЖИТЕЛЬНОГО ЧИСЛА
r
Х
Слайд 26Кругом называют ГМТ, расстояние от которых до заданной точки не
больше данного положительного числа
r
Х
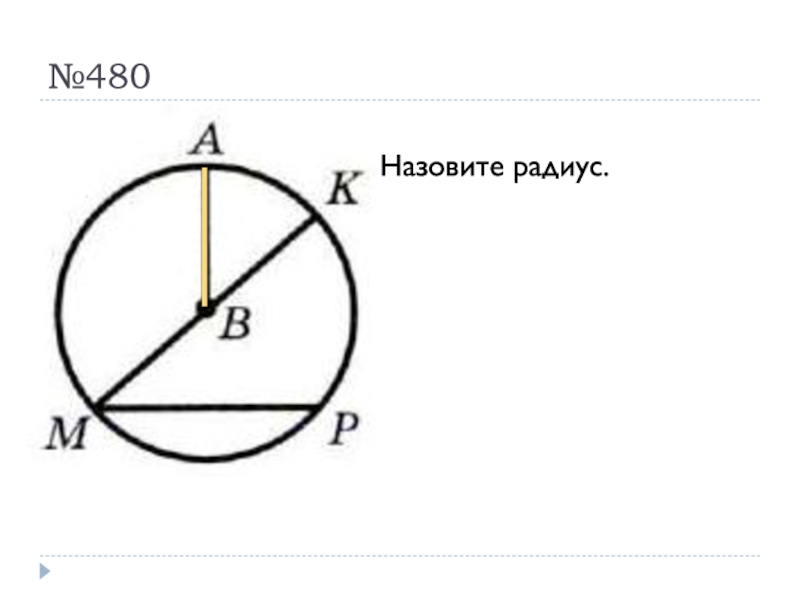
Слайд 36№480
Назовите радиус.
Назовите хорду.
Назовите диаметр.
Сколько радиусов на чертеже?
Сколько хорд на чертеже?
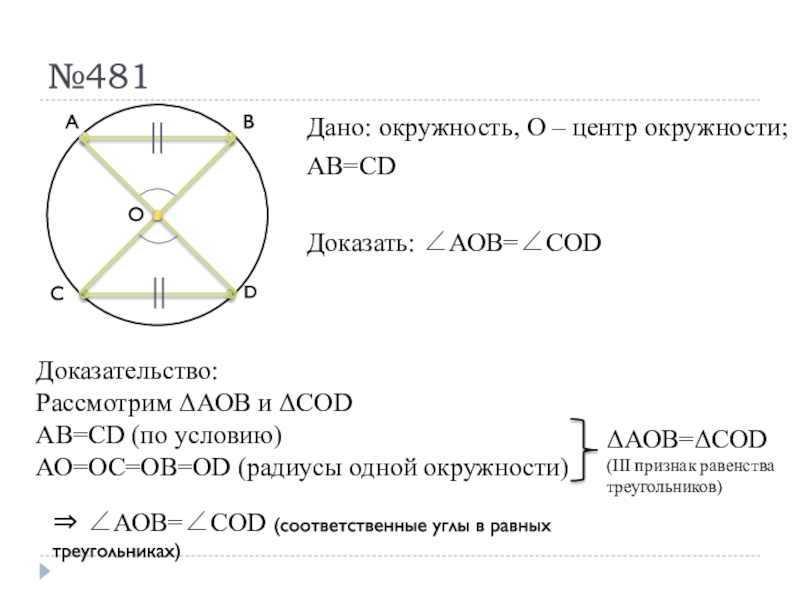
Слайд 39№481
Дано: окружность, О – центр окружности;
АВ=СD
Доказать: АОВ=СOD
О
А
D
С
В
Доказательство:
Рассмотрим АОВ и СОD
АВ=СD
(по условию)
АО=ОС=ОВ=ОD (радиусы одной окружности)
АОВ=СОD (III признак равенства треугольников)
АОВ=СOD
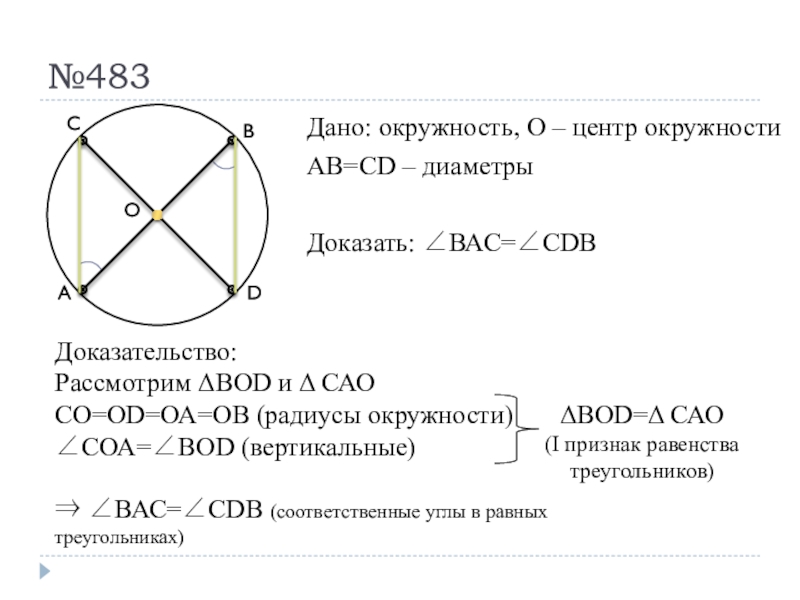
(соответственные углы в равных треугольниках) 
Слайд 40№483
Дано: окружность, О – центр окружности
АВ=СD – диаметры
Доказать: ВАС=СDВ
О
С
D
А
В
Доказательство:
Рассмотрим ВОD и САО
СО=ОD=ОА=ОВ (радиусы окружности)
СОА=ВОD (вертикальные)
ВОD= САО
(I признак
равенства треугольников) ВАС=СDВ (соответственные углы в равных треугольниках)
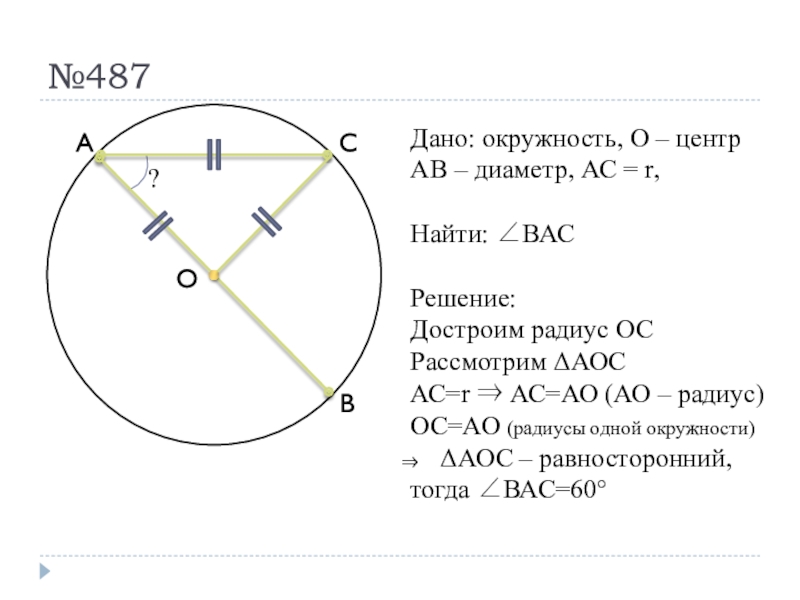
Слайд 42№487
О
А
В
С
?
Дано: окружность, О – центр
АВ – диаметр, АС =
r,
Найти: ВАС
Решение:
Достроим радиус ОС
Рассмотрим АОС
АС=r АС=АО (АО – радиус)
ОС=АО
(радиусы одной окружности)АОС – равносторонний,
тогда ВАС=60°
Слайд 44Самостоятельная работа
(выполнить в тетради для ДЗ и выслать фото)
№1
Запишите все изображенные радиусы: _____________________
Запишите все изображенные хорды: _______________________
Запишите все
изображенные диаметры: ____________________№2
Чему равен диаметр окружности, если известно, что он на 3 см больше ее радиуса?
Ответ: _________
№3
Начертите окружность с центром А и радиусом 2 см. Проведите в этой окружности радиус АС, диаметр МК, хорду ВР, не являющуюся диаметром. Найдите на окружности точки, удаленные точки М на 1,5 см.
