Разделы презентаций

1 Эксперимент по методу Монте-Карло Согласно материалу, представленном в

Содержание

2На этом слайде мы непосредственно исследуем влияние ошибки на b2, используя эксперимент Монте-Карло (имитационный эксперимент). Эксперимент по методу Монте-КарлоИстинная модель Соответствующая модель

Слайды и текст этой презентации

Слайд 1




1
Эксперимент по методу Монте-Карло
Согласно материалу, представленном в предыдущей презентации, мы

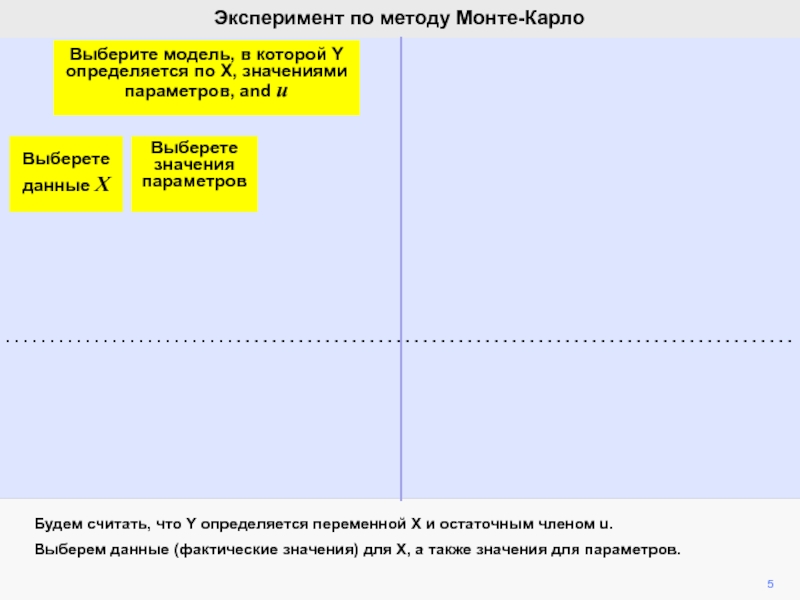
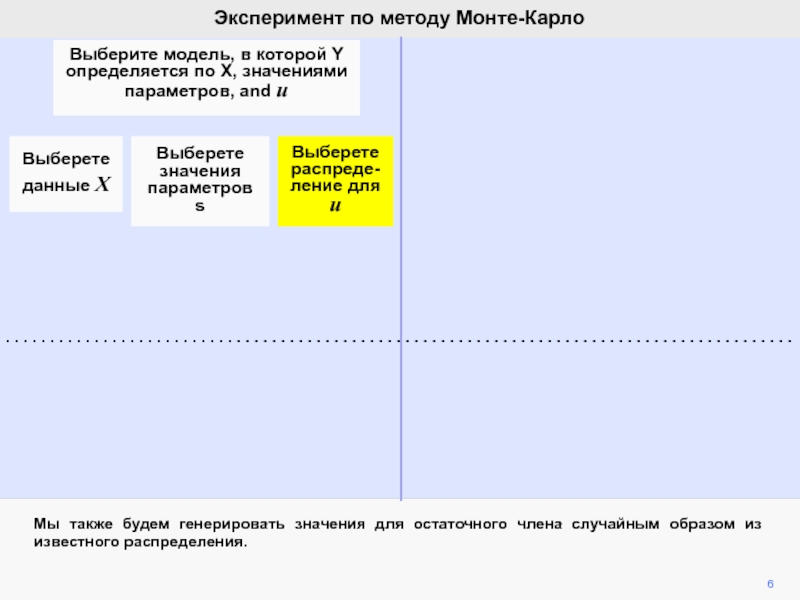
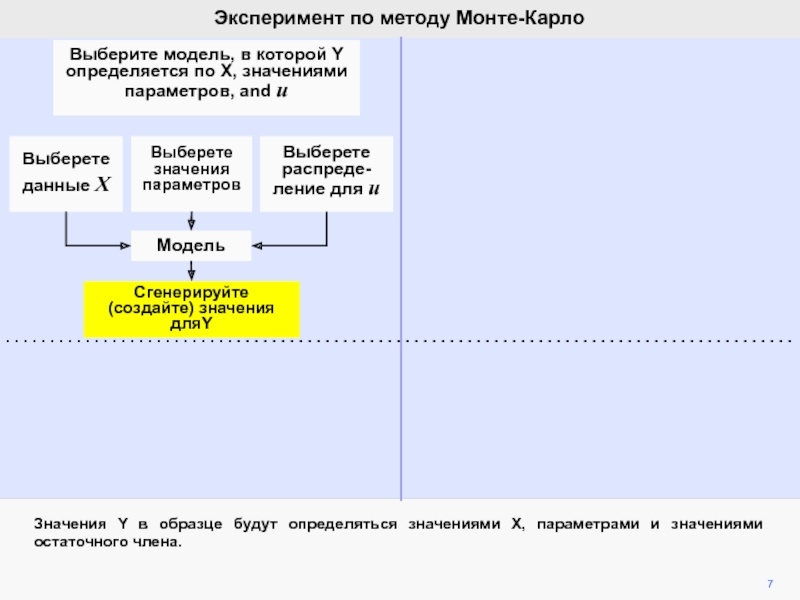
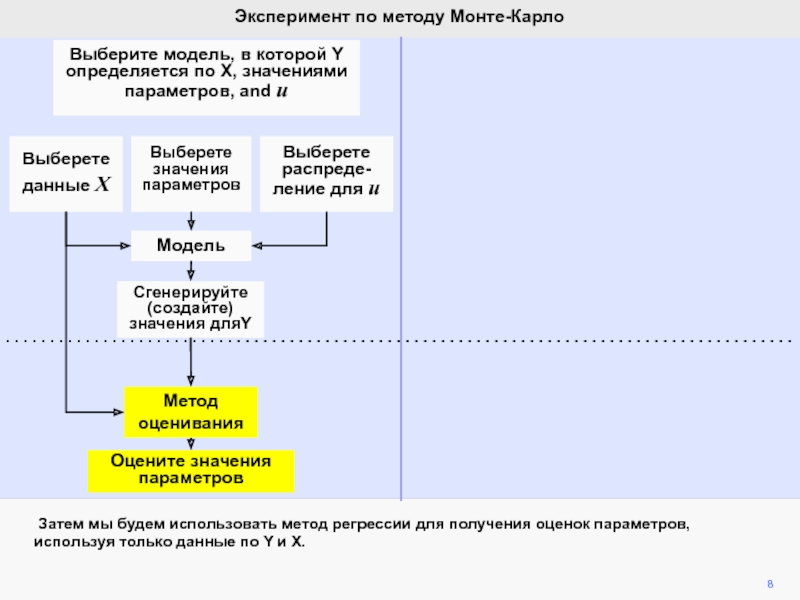
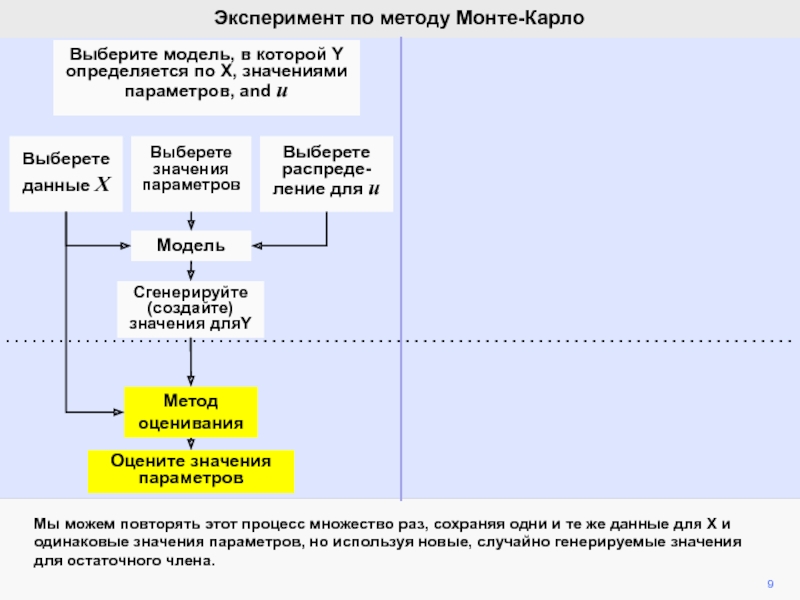
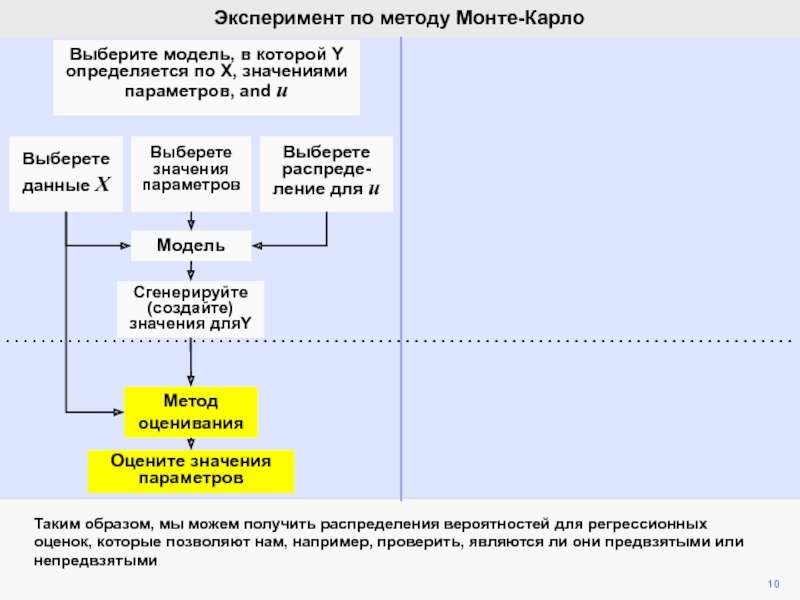
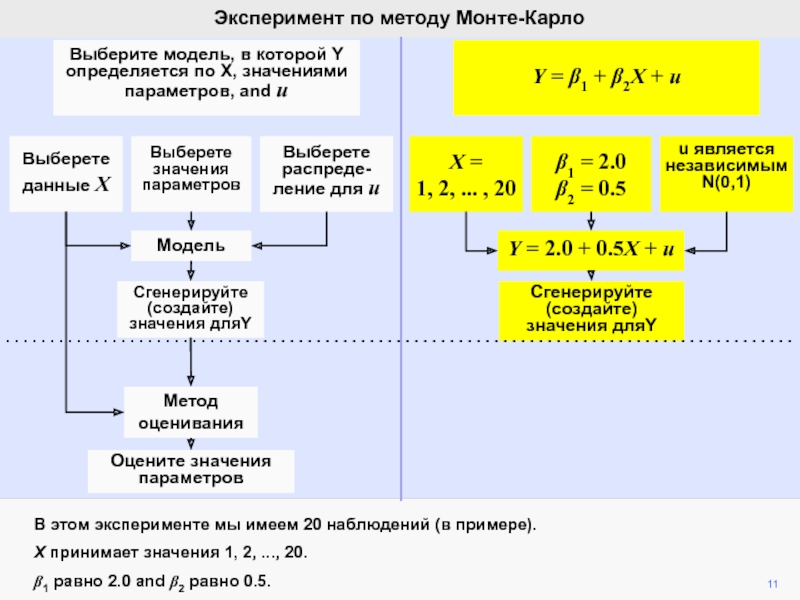
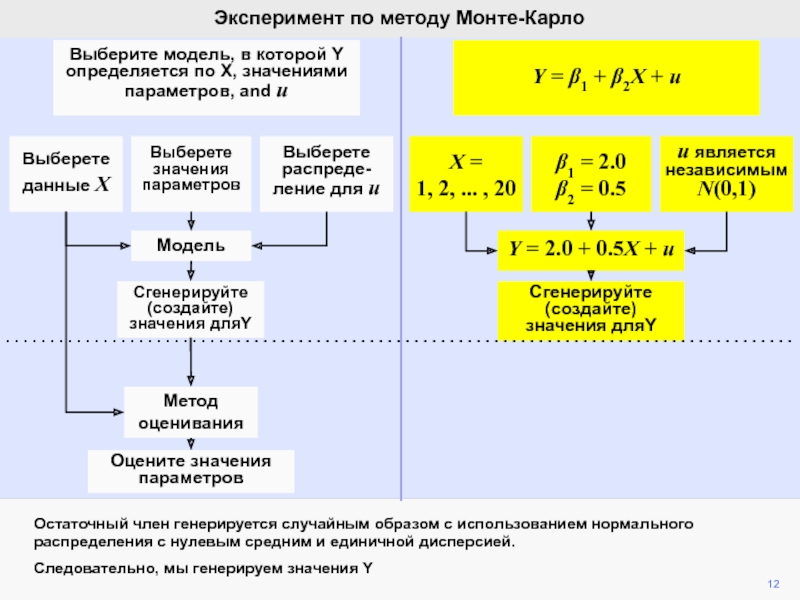
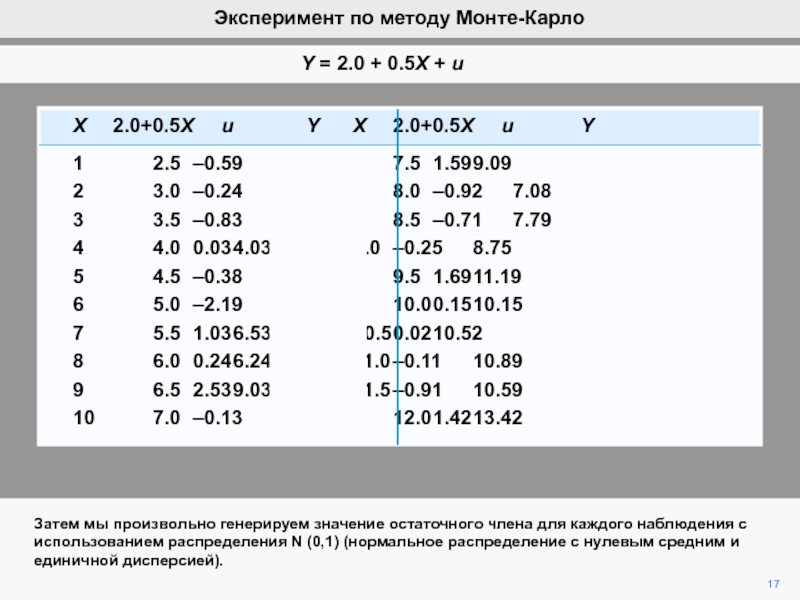
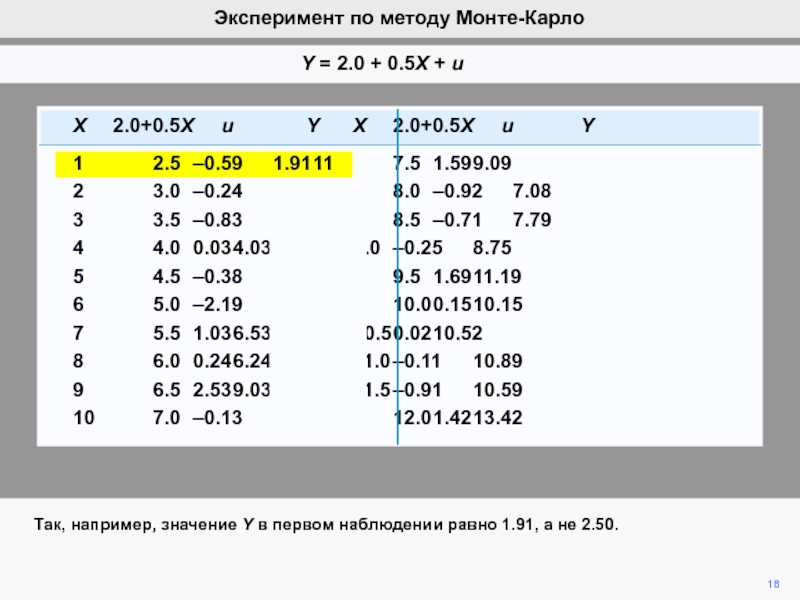
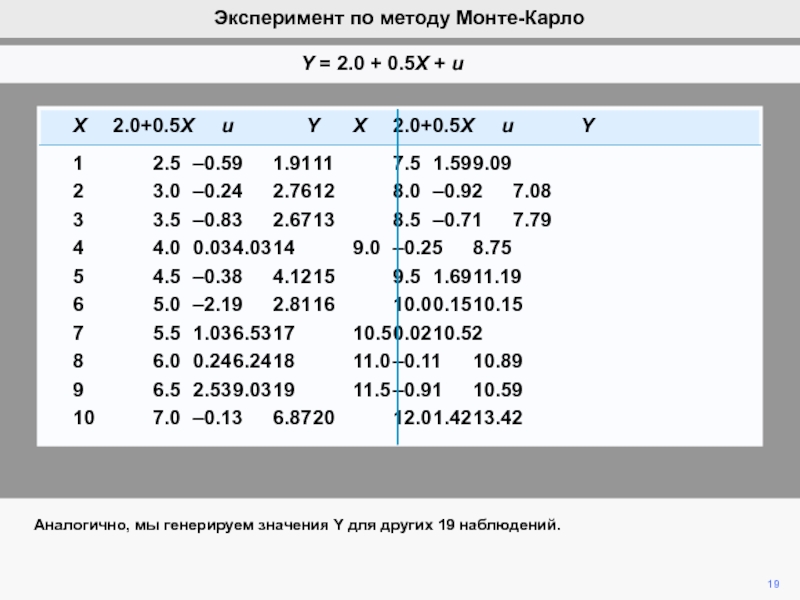
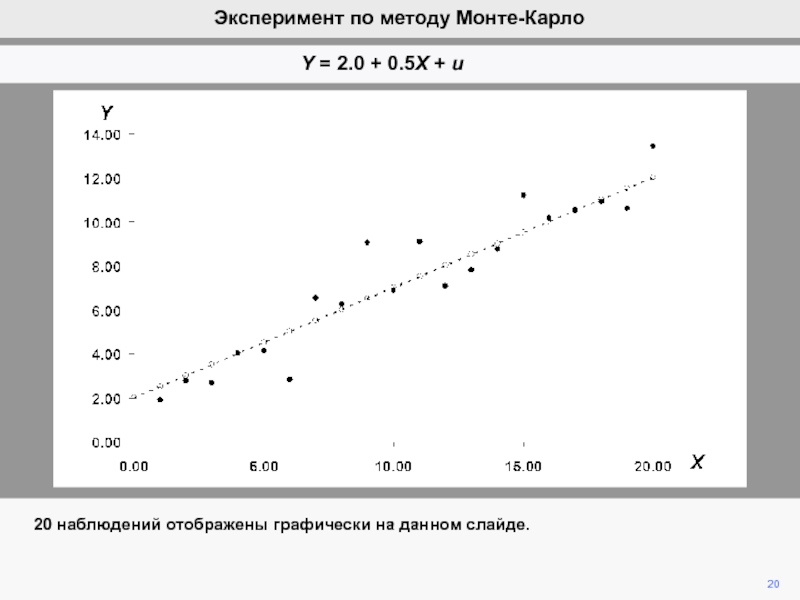
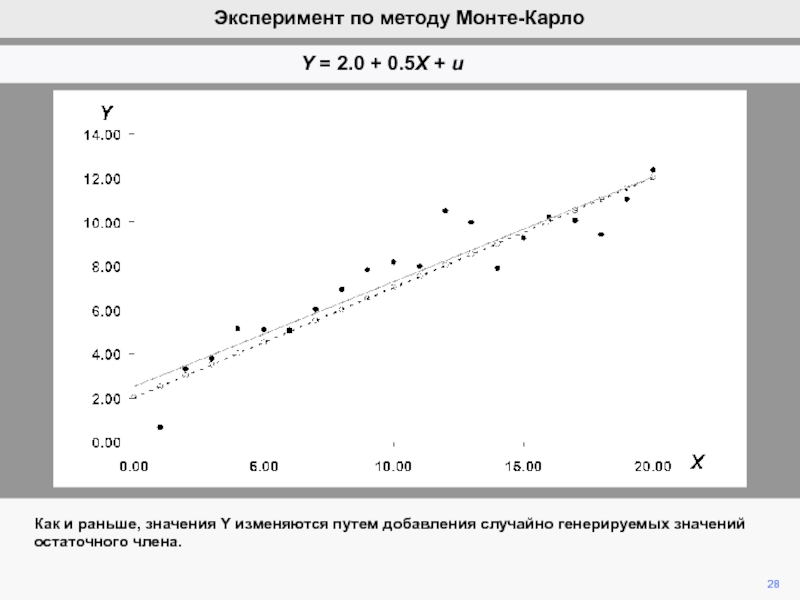
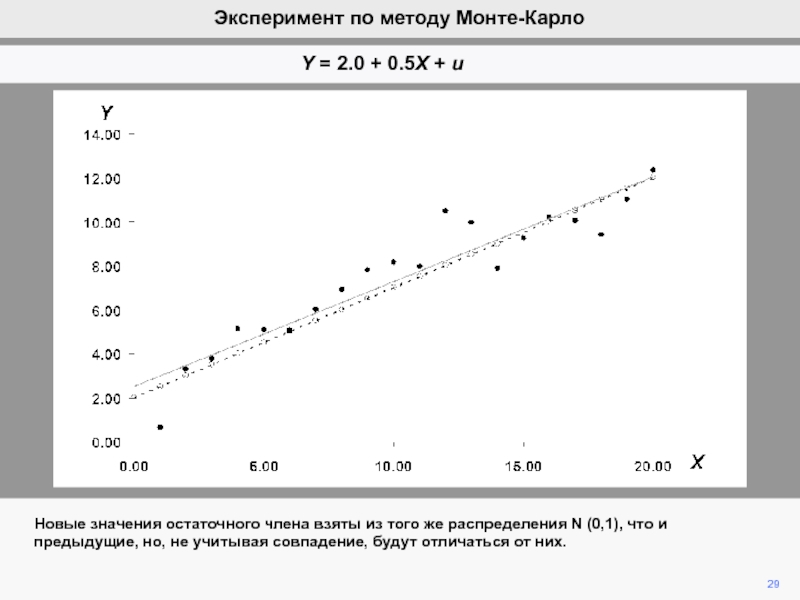
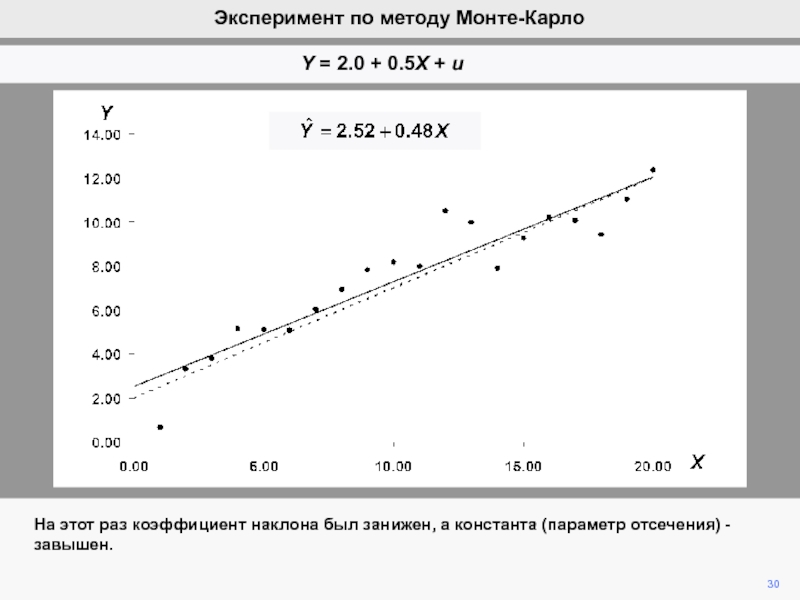
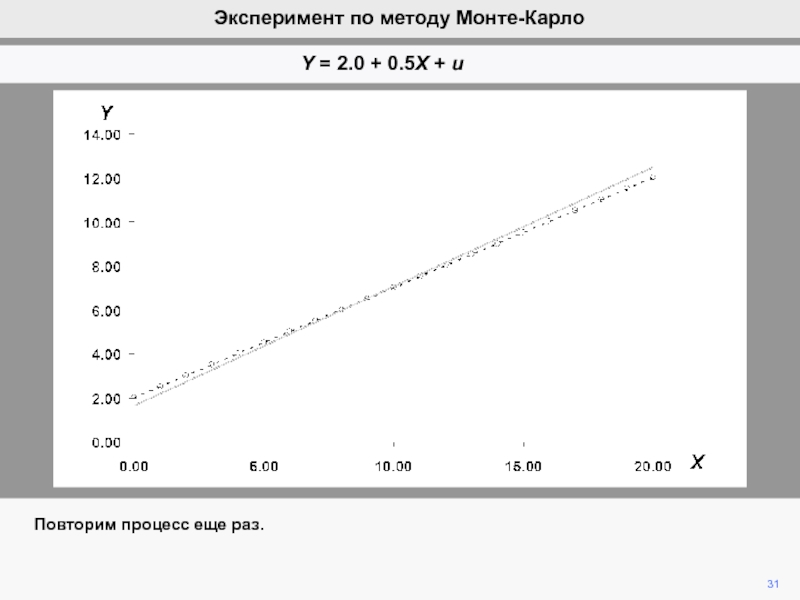
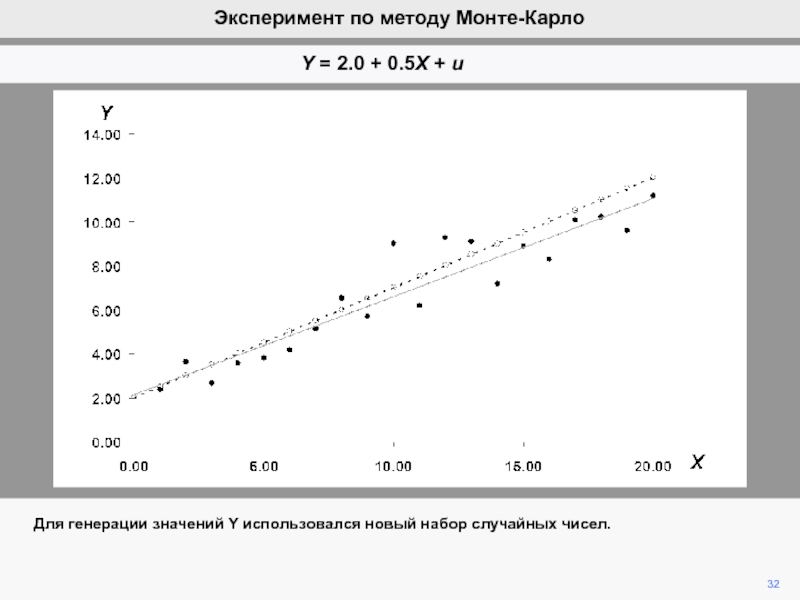
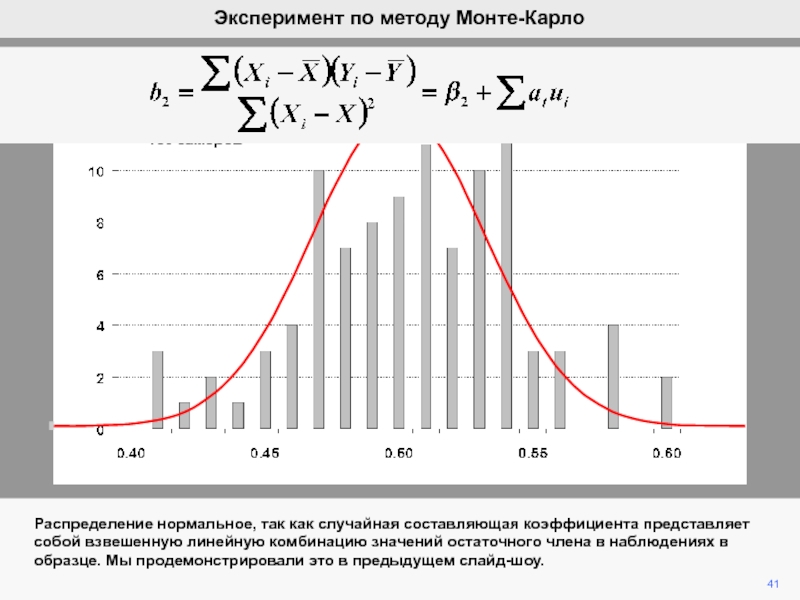
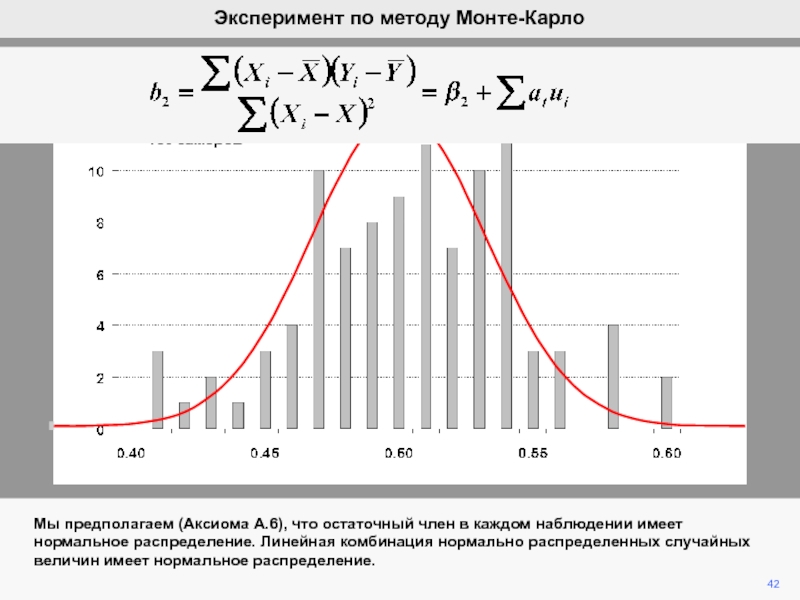
видим, что ошибка ответственна за вариации b2 при фиксированной компоненте

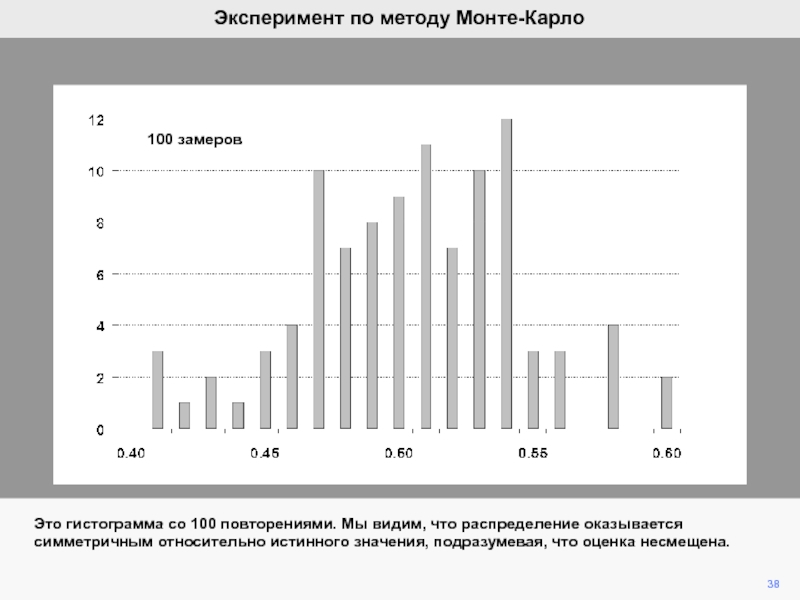
b2.
Мы математически продемонстрировали, что ожидание ошибки равно нулю, а, следовательно, b2 является несмещенной оценкой of b2.

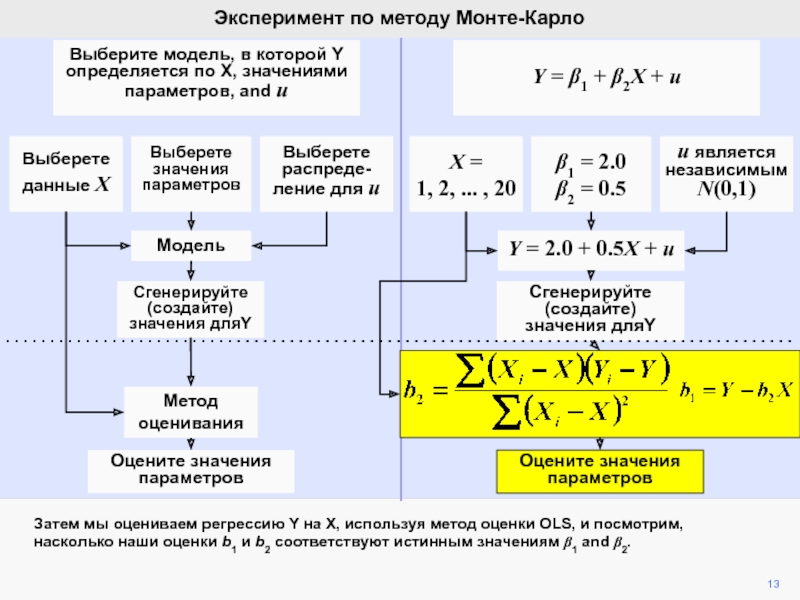
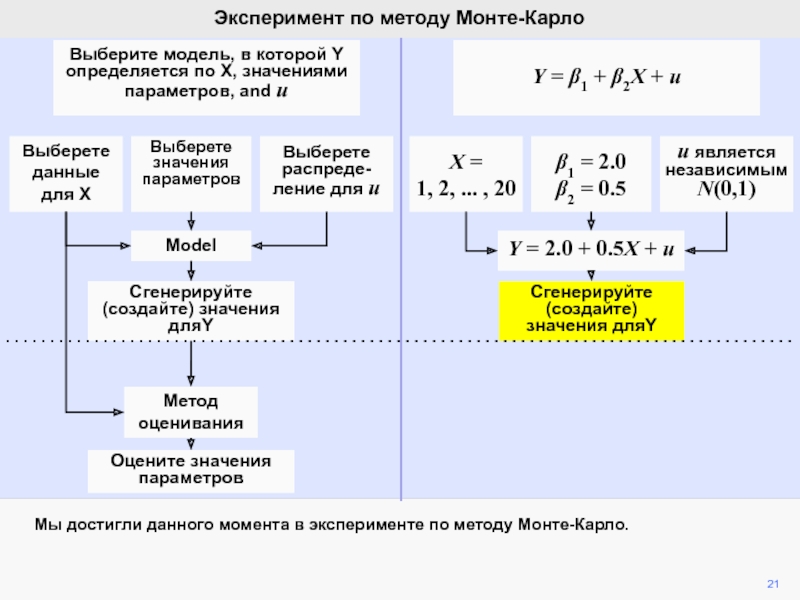
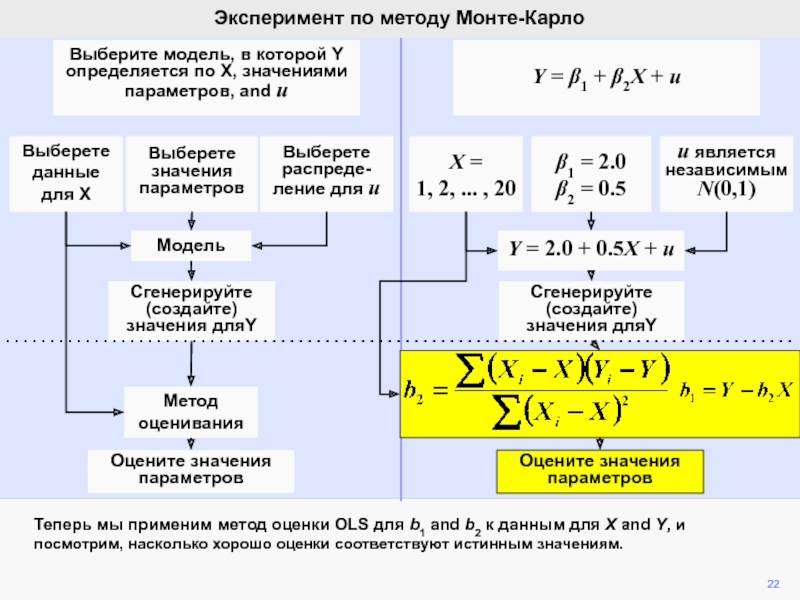
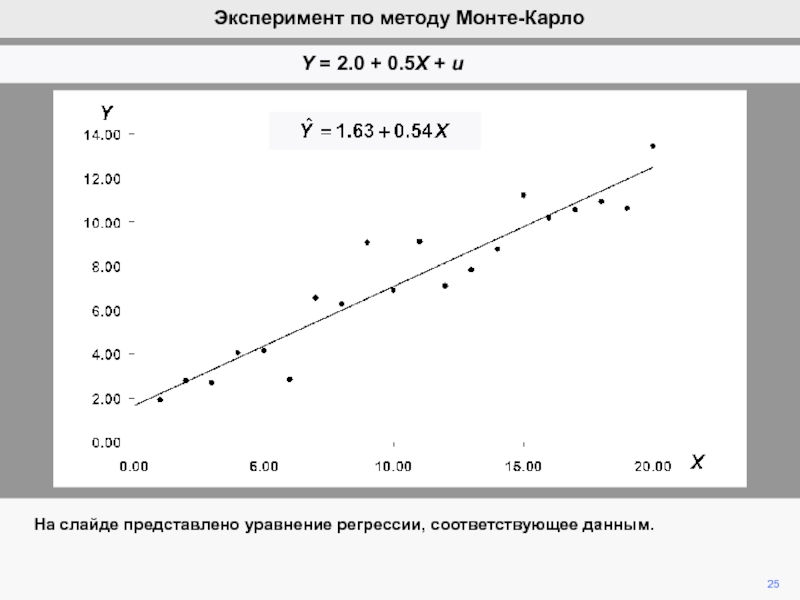
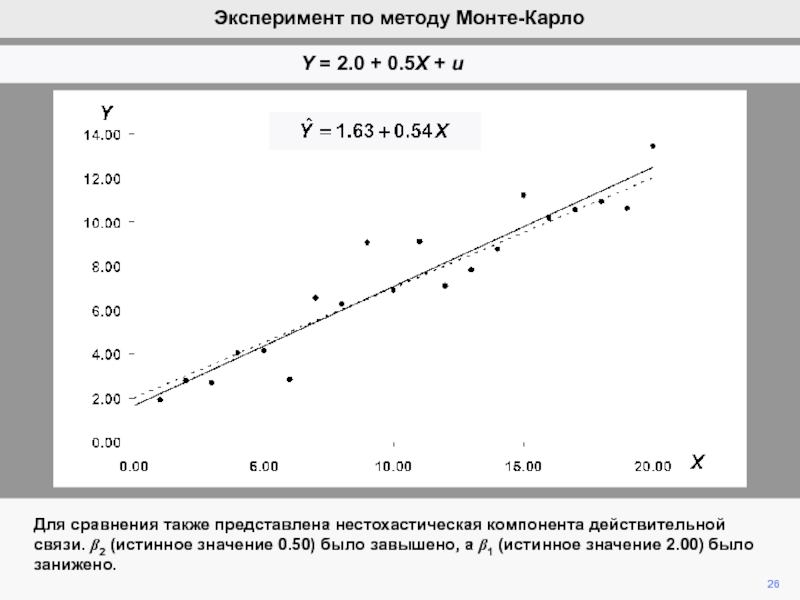
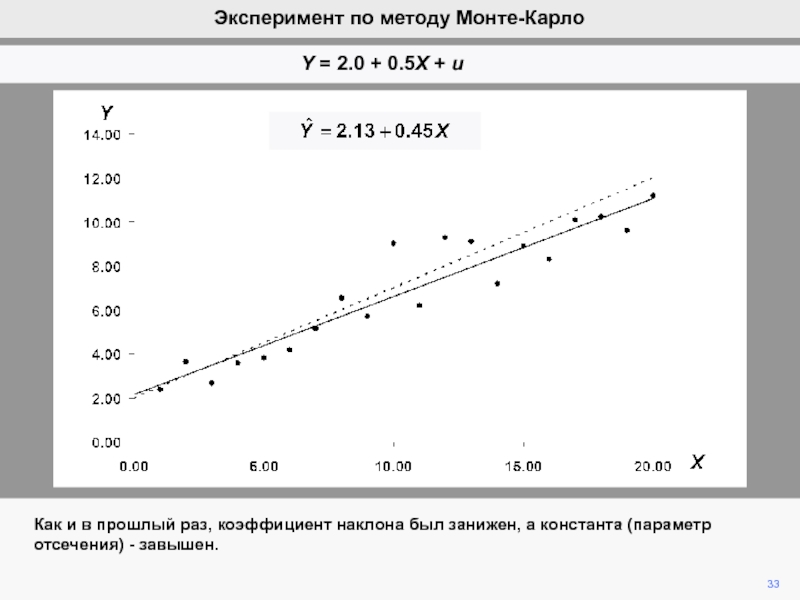
Истинная модель Соответствующая модель

1Эксперимент по методу Монте-КарлоСогласно материалу, представленном в предыдущей презентации, мы видим, что ошибка ответственна за вариации b2

Слайд 22
На этом слайде мы непосредственно исследуем влияние ошибки на b2,

используя эксперимент Монте-Карло (имитационный эксперимент). 
Эксперимент по методу Монте-Карло

Истинная модель

Соответствующая модель
2На этом слайде мы непосредственно исследуем влияние ошибки на b2, используя эксперимент Монте-Карло (имитационный эксперимент). Эксперимент по методу

Слайд 33
Эксперимент по методу Монте-Карло - это лабораторное исследование, обычно проводимое

с целью оценки свойств регрессионных оценок в контролируемых условиях. 
Эксперимент по

методу Монте-Карло

  Выберите модель, в которой Y определяется по X, значениями параметров, and u

3Эксперимент по методу Монте-Карло - это лабораторное исследование, обычно проводимое с целью оценки свойств регрессионных оценок в

Слайд 44
Мы будем использовать эксперимент по методу Монте-Карло для исследования поведения

регрессионных коэффициентов OLS , применимо к простой модели регрессии.
Эксперимент по

методу Монте-Карло

Выберите модель, в которой Y определяется по X, значениями параметров, and u

4Мы будем использовать эксперимент по методу Монте-Карло для исследования поведения регрессионных коэффициентов OLS , применимо к простой

Слайд 55
Будем считать, что Y определяется переменной X и остаточным членом

u.
Выберем данные (фактические значения) для X, а также значения для

параметров. 

Эксперимент по методу Монте-Карло


Выберете данные X

Выберете значения параметров

Выберите модель, в которой Y определяется по X, значениями параметров, and u

5Будем считать, что Y определяется переменной X и остаточным членом u.Выберем данные (фактические значения) для X, а

Слайд 66
Мы также будем генерировать значения для остаточного члена случайным образом

из известного распределения.
Эксперимент по методу Монте-Карло

Выберете данные X

Выберете значения параметров
s

Выберете

распреде-ление для u

Выберите модель, в которой Y определяется по X, значениями параметров, and u

6Мы также будем генерировать значения для остаточного члена случайным образом из известного распределения.Эксперимент по методу Монте-КарлоВыберете данные

Слайд 77
Значения Y в образце будут определяться значениями X, параметрами и

значениями остаточного члена.
Эксперимент по методу Монте-Карло

Выберете данные X

Выберете значения параметров

Выберете

распреде-ление для u

Модель

Сгенерируйте (создайте) значения дляY

Выберите модель, в которой Y определяется по X, значениями параметров, and u

7Значения Y в образце будут определяться значениями X, параметрами и значениями остаточного члена.Эксперимент по методу Монте-КарлоВыберете данные

Слайд 88
 Затем мы будем использовать метод регрессии для получения оценок параметров,

используя только данные по Y и X.
Эксперимент по методу Монте-Карло


Выберете

данные X


Выберете значения параметров


Выберете распреде-ление для u

Модель

Сгенерируйте (создайте) значения дляY

Метод оценивания

Оцените значения параметров

Выберите модель, в которой Y определяется по X, значениями параметров, and u

8 Затем мы будем использовать метод регрессии для получения оценок параметров, используя только данные по Y и X.Эксперимент

Слайд 99
Мы можем повторять этот процесс множество раз, сохраняя одни и

те же данные для X и одинаковые значения параметров, но

используя новые, случайно генерируемые значения для остаточного члена.

Эксперимент по методу Монте-Карло


Выберете данные X


Выберете значения параметров


Выберете распреде-ление для u

Модель

Сгенерируйте (создайте) значения дляY

Метод оценивания

Оцените значения параметров

Выберите модель, в которой Y определяется по X, значениями параметров, and u

9Мы можем повторять этот процесс множество раз, сохраняя одни и те же данные для X и одинаковые

Слайд 1010
Таким образом, мы можем получить распределения вероятностей для регрессионных оценок,

которые позволяют нам, например, проверить, являются ли они предвзятыми или

непредвзятыми

Эксперимент по методу Монте-Карло


Выберете данные X


Выберете значения параметров


Выберете распреде-ление для u

Модель

Сгенерируйте (создайте) значения дляY

Метод оценивания

Оцените значения параметров

Выберите модель, в которой Y определяется по X, значениями параметров, and u

10Таким образом, мы можем получить распределения вероятностей для регрессионных оценок, которые позволяют нам, например, проверить, являются ли

Слайд 1111
В этом эксперименте мы имеем 20 наблюдений (в примере).
X

принимает значения 1, 2, ..., 20.
b1 равно 2.0 and

b2 равно 0.5.

Эксперимент по методу Монте-Карло


Выберете данные X


Выберете значения параметров


Выберете распреде-ление для u

Модель

Сгенерируйте (создайте) значения дляY

Метод оценивания

Оцените значения параметров


Y = b1 + b2X + u


X =
1, 2, ... , 20


b1 = 2.0
b2 = 0.5

u является независимымN(0,1)

Y = 2.0 + 0.5X + u

Сгенерируйте (создайте) значения дляY

Выберите модель, в которой Y определяется по X, значениями параметров, and u

11В этом эксперименте мы имеем 20 наблюдений (в примере). X принимает значения 1, 2, ..., 20. b1

Слайд 1212
Остаточный член генерируется случайным образом с использованием нормального распределения с

нулевым средним и единичной дисперсией.
Следовательно, мы генерируем значения Y
Эксперимент по

методу Монте-Карло


Выберете данные X


Выберете значения параметров


Выберете распреде-ление для u

Модель

Сгенерируйте (создайте) значения дляY

Метод оценивания

Оцените значения параметров


Y = b1 + b2X + u


X =
1, 2, ... , 20


b1 = 2.0
b2 = 0.5

u является независимымN(0,1)

Y = 2.0 + 0.5X + u

Сгенерируйте (создайте) значения дляY

Выберите модель, в которой Y определяется по X, значениями параметров, and u

12Остаточный член генерируется случайным образом с использованием нормального распределения с нулевым средним и единичной дисперсией.Следовательно, мы генерируем

Слайд 1313
Затем мы оцениваем регрессию Y на X, используя метод оценки

OLS, и посмотрим, насколько наши оценки b1 и b2 соответствуют

истинным значениям b1 and b2.


Выберете данные X


Выберете значения параметров


Выберете распреде-ление для u

Модель

Сгенерируйте (создайте) значения дляY

Метод оценивания

Оцените значения параметров


Y = b1 + b2X + u


X =
1, 2, ... , 20


b1 = 2.0
b2 = 0.5

u является независимымN(0,1)

Y = 2.0 + 0.5X + u

Сгенерируйте (создайте) значения дляY


Оцените значения параметров

Эксперимент по методу Монте-Карло

Выберите модель, в которой Y определяется по X, значениями параметров, and u

13Затем мы оцениваем регрессию Y на X, используя метод оценки OLS, и посмотрим, насколько наши оценки b1

Слайд 14На данном слайде представлены значения X, выбранные совершенно произвольно
14
Эксперимент по

методу Монте-Карло
X 2.0+0.5X u

Y X 2.0+0.5X u Y
1 2.5 –0.59 1.91 11 7.5 1.59 9.09
2 3.0 –0.24 2.76 12 8.0 –0.92 7.08
3 3.5 –0.83 2.67 13 8.5 –0.71 7.79
4 4.0 0.03 4.03 14 9.0 –0.25 8.75
5 4.5 –0.38 4.12 15 9.5 1.69 11.19
6 5.0 –2.19 2.81 16 10.0 0.15 10.15
7 5.5 1.03 6.53 17 10.5 0.02 10.52
8 6.0 0.24 6.24 18 11.0 –0.11 10.89
9 6.5 2.53 9.03 19 11.5 –0.91 10.59
10 7.0 –0.13 6.87 20 12.0 1.42 13.42

Y = 2.0 + 0.5X + u

На данном слайде представлены значения X, выбранные совершенно произвольно14Эксперимент по методу Монте-Карло X 2.0+0.5X u

Слайд 15Учитывая выбор чисел для b1 and b2, мы можем получить

нестахостическую компонентуY.
15
Эксперимент по методу Монте-Карло
X 2.0+0.5X u

Y X 2.0+0.5X u Y
1 2.5 –0.59 1.91 11 7.5 1.59 9.09
2 3.0 –0.24 2.76 12 8.0 –0.92 7.08
3 3.5 –0.83 2.67 13 8.5 –0.71 7.79
4 4.0 0.03 4.03 14 9.0 –0.25 8.75
5 4.5 –0.38 4.12 15 9.5 1.69 11.19
6 5.0 –2.19 2.81 16 10.0 0.15 10.15
7 5.5 1.03 6.53 17 10.5 0.02 10.52
8 6.0 0.24 6.24 18 11.0 –0.11 10.89
9 6.5 2.53 9.03 19 11.5 –0.91 10.59
10 7.0 –0.13 6.87 20 12.0 1.42 13.42

Y = 2.0 + 0.5X + u

Учитывая выбор чисел для b1 and b2, мы можем получить нестахостическую компонентуY.15Эксперимент по методу Монте-Карло X 2.0+0.5X

Слайд 16Нестахостическая компонента отображена на графике.
16
Эксперимент по методу Монте-Карло
Y = 2.0

+ 0.5X + u

Нестахостическая компонента отображена на графике.16Эксперимент по методу Монте-КарлоY = 2.0 + 0.5X + u

Слайд 17Затем мы произвольно генерируем значение остаточного члена для каждого наблюдения

с использованием распределения N (0,1) (нормальное распределение с нулевым средним

и единичной дисперсией). 

17

Эксперимент по методу Монте-Карло

X 2.0+0.5X u Y X 2.0+0.5X u Y
1 2.5 –0.59 1.91 11 7.5 1.59 9.09
2 3.0 –0.24 2.76 12 8.0 –0.92 7.08
3 3.5 –0.83 2.67 13 8.5 –0.71 7.79
4 4.0 0.03 4.03 14 9.0 –0.25 8.75
5 4.5 –0.38 4.12 15 9.5 1.69 11.19
6 5.0 –2.19 2.81 16 10.0 0.15 10.15
7 5.5 1.03 6.53 17 10.5 0.02 10.52
8 6.0 0.24 6.24 18 11.0 –0.11 10.89
9 6.5 2.53 9.03 19 11.5 –0.91 10.59
10 7.0 –0.13 6.87 20 12.0 1.42 13.42

Y = 2.0 + 0.5X + u

Затем мы произвольно генерируем значение остаточного члена для каждого наблюдения с использованием распределения N (0,1) (нормальное распределение

Слайд 1818
Эксперимент по методу Монте-Карло
X 2.0+0.5X u

Y X 2.0+0.5X u

Y
1 2.5 –0.59 1.91 11 7.5 1.59 9.09
2 3.0 –0.24 2.76 12 8.0 –0.92 7.08
3 3.5 –0.83 2.67 13 8.5 –0.71 7.79
4 4.0 0.03 4.03 14 9.0 –0.25 8.75
5 4.5 –0.38 4.12 15 9.5 1.69 11.19
6 5.0 –2.19 2.81 16 10.0 0.15 10.15
7 5.5 1.03 6.53 17 10.5 0.02 10.52
8 6.0 0.24 6.24 18 11.0 –0.11 10.89
9 6.5 2.53 9.03 19 11.5 –0.91 10.59
10 7.0 –0.13 6.87 20 12.0 1.42 13.42

Так, например, значение Y в первом наблюдении равно 1.91, а не 2.50.

Y = 2.0 + 0.5X + u

18Эксперимент по методу Монте-Карло X 2.0+0.5X u Y X 2.0+0.5X

Слайд 1919
Аналогично, мы генерируем значения Y для других 19 наблюдений.
Эксперимент по

методу Монте-Карло
X 2.0+0.5X u

Y X 2.0+0.5X u Y
1 2.5 –0.59 1.91 11 7.5 1.59 9.09
2 3.0 –0.24 2.76 12 8.0 –0.92 7.08
3 3.5 –0.83 2.67 13 8.5 –0.71 7.79
4 4.0 0.03 4.03 14 9.0 –0.25 8.75
5 4.5 –0.38 4.12 15 9.5 1.69 11.19
6 5.0 –2.19 2.81 16 10.0 0.15 10.15
7 5.5 1.03 6.53 17 10.5 0.02 10.52
8 6.0 0.24 6.24 18 11.0 –0.11 10.89
9 6.5 2.53 9.03 19 11.5 –0.91 10.59
10 7.0 –0.13 6.87 20 12.0 1.42 13.42

Y = 2.0 + 0.5X + u

19Аналогично, мы генерируем значения Y для других 19 наблюдений.Эксперимент по методу Монте-Карло X 2.0+0.5X u

Слайд 2020 наблюдений отображены графически на данном слайде.
20
Эксперимент по методу Монте-Карло
Y

= 2.0 + 0.5X + u

20 наблюдений отображены графически на данном слайде.20Эксперимент по методу Монте-КарлоY = 2.0 + 0.5X + u

Слайд 21Мы достигли данного момента в эксперименте по методу Монте-Карло.
21
A MONTE

CARLO EXPERIMENT
Выберете данные для X
Выберете значения параметров

Выберете распреде-ление для u
Model
Сгенерируйте

(создайте) значения дляY

Метод оценивания

Оцените значения параметров


Y = b1 + b2X + u


X =
1, 2, ... , 20


b1 = 2.0
b2 = 0.5

u является независимымN(0,1)

Y = 2.0 + 0.5X + u

Сгенерируйте (создайте) значения дляY

Эксперимент по методу Монте-Карло

Выберите модель, в которой Y определяется по X, значениями параметров, and u

Мы достигли данного момента в эксперименте по методу Монте-Карло.21A MONTE CARLO EXPERIMENTВыберете данные для XВыберете значения параметровВыберете

Слайд 22Теперь мы применим метод оценки OLS для b1 and b2

к данным для X and Y, и посмотрим, насколько хорошо

оценки соответствуют истинным значениям.

22

Выберете данные для X


Выберете значения параметров


Выберете распреде-ление для u

Модель

Сгенерируйте (создайте) значения дляY

Метод оценивания

Оцените значения параметров


Y = b1 + b2X + u


X =
1, 2, ... , 20


b1 = 2.0
b2 = 0.5

u является независимымN(0,1)

Y = 2.0 + 0.5X + u

Сгенерируйте (создайте) значения дляY


Оцените значения параметров

Эксперимент по методу Монте-Карло

Выберите модель, в которой Y определяется по X, значениями параметров, and u

Теперь мы применим метод оценки OLS для b1 and b2 к данным для X and Y, и

Слайд 23На данном слайде снова представлена диаграмма дисперсии (корреляционная диаграмма).
23
Эксперимент по

методу Монте-Карло
Y = 2.0 + 0.5X + u

На данном слайде снова представлена диаграмма дисперсии (корреляционная диаграмма).23Эксперимент по методу Монте-КарлоY = 2.0 + 0.5X +

Слайд 24Метод оценки использует только наблюдаемые данные для X and Y.
24
Эксперимент

по методу Монте-Карло
Y = 2.0 + 0.5X + u

Метод оценки использует только наблюдаемые данные для X and Y.24Эксперимент по методу Монте-КарлоY = 2.0 + 0.5X

Слайд 25На слайде представлено уравнение регрессии, соответствующее данным.
25
Эксперимент по методу Монте-Карло
Y

= 2.0 + 0.5X + u

На слайде представлено уравнение регрессии, соответствующее данным.25Эксперимент по методу Монте-КарлоY = 2.0 + 0.5X + u

Слайд 26Для сравнения также представлена нестохастическая компонента действительной связи. b2 (истинное

значение 0.50) было завышено, а b1 (истинное значение 2.00) было

занижено.

26

Эксперимент по методу Монте-Карло

Y = 2.0 + 0.5X + u

Для сравнения также представлена нестохастическая компонента действительной связи. b2 (истинное значение 0.50) было завышено, а b1 (истинное

Слайд 27Мы повторим процесс, начиная с тех же нестахостических компонент Y.
27
Эксперимент

по методу Монте-Карло
Y = 2.0 + 0.5X + u

Мы повторим процесс, начиная с тех же нестахостических компонент Y.27Эксперимент по методу Монте-КарлоY = 2.0 + 0.5X

Слайд 28Как и раньше, значения Y изменяются путем добавления случайно генерируемых

значений остаточного члена.
28
Эксперимент по методу Монте-Карло
Y = 2.0 + 0.5X

+ u
Как и раньше, значения Y изменяются путем добавления случайно генерируемых значений остаточного члена.28Эксперимент по методу Монте-КарлоY =

Слайд 29Новые значения остаточного члена взяты из того же распределения N

(0,1), что и предыдущие, но, не учитывая совпадение, будут отличаться

от них. 

29

Эксперимент по методу Монте-Карло

Y = 2.0 + 0.5X + u

Новые значения остаточного члена взяты из того же распределения N (0,1), что и предыдущие, но, не учитывая

Слайд 30На этот раз коэффициент наклона был занижен, а константа (параметр

отсечения) - завышен.
30
Эксперимент по методу Монте-Карло
Y = 2.0 + 0.5X

+ u
На этот раз коэффициент наклона был занижен, а константа (параметр отсечения) - завышен.30Эксперимент по методу Монте-КарлоY =

Слайд 31Повторим процесс еще раз.
31
Эксперимент по методу Монте-Карло
Y = 2.0 +

0.5X + u

Повторим процесс еще раз.31Эксперимент по методу Монте-КарлоY = 2.0 + 0.5X + u

Слайд 32Для генерации значений Y использовался новый набор случайных чисел.
32
Эксперимент по

методу Монте-Карло
Y = 2.0 + 0.5X + u

Для генерации значений Y использовался новый набор случайных чисел.32Эксперимент по методу Монте-КарлоY = 2.0 + 0.5X +

Слайд 33Как и в прошлый раз, коэффициент наклона был занижен, а

константа (параметр отсечения) - завышен.
33
Эксперимент по методу Монте-Карло
Y = 2.0

+ 0.5X + u
Как и в прошлый раз, коэффициент наклона был занижен, а константа (параметр отсечения) - завышен.33Эксперимент по методу

Слайд 34В таблице приведены результаты трех регрессий и добавлены полученные результаты,

повторяющие этот процесс еще семь раз. 
34

Модель b1 b2
1 1.63 0.54
2 2.52 0.48
3 2.13 0.45
4 2.14 0.50
5 1.71 0.56
6 1.81 0.51
7 1.72 0.56
8 3.18 0.41
9 1.26 0.58
10 1.94 0.52

Эксперимент по методу Монте-Карло

В таблице приведены результаты трех регрессий и добавлены полученные результаты, повторяющие этот процесс еще семь раз. 34

Слайд 35На данном слайде представлена гистограмма для оценок b2.
Особых изменений

не было замечено.
35
Эксперимент по методу Монте-Карло
10 замеров

На данном слайде представлена гистограмма для оценок b2. Особых изменений не было замечено.35Эксперимент по методу Монте-Карло10 замеров

Слайд 36В данной таблице приведены оценки b2 , полученные в ходе

повторения процесса еще 40 раз.

36

1-10 11-20 21-30 31-40 41-50
0.54 0.49 0.54 0.52 0.49
0.48 0.54 0.46 0.47 0.50
0.45 0.49 0.45 0.54 0.48
0.50 0.54 0.50 0.53 0.44
0.56 0.54 0.41 0.51 0.53
0.51 0.52 0.53 0.51 0.48
0.56 0.49 0.53 0.47 0.47
0.41 0.53 0.47 0.55 0.50
0.58 0.60 0.51 0.51 0.53
0.52 0.48 0.47 0.58 0.51

Эксперимент по методу Монте-Карло

В данной таблице приведены оценки b2 , полученные в ходе повторения процесса еще 40 раз.36

Слайд 37Гистограмма начинает проявлять центральную тенденцию.
37
Эксперимент по методу Монте-Карло
50 замеров

Гистограмма начинает проявлять центральную тенденцию.37Эксперимент по методу Монте-Карло50 замеров

Слайд 38Это гистограмма со 100 повторениями. Мы видим, что распределение оказывается симметричным

относительно истинного значения, подразумевая, что оценка несмещена.
38
Эксперимент по методу Монте-Карло
100

замеров
Это гистограмма со 100 повторениями. Мы видим, что распределение оказывается симметричным относительно истинного значения, подразумевая, что оценка несмещена.38Эксперимент

Слайд 39Однако, распределение все еще является довольно неровным. Было бы лучше

повторить процесс 1,000,000 раз, возможно, даже больше.
39
Эксперимент по методу Монте-Карло
100

замеров
Однако, распределение все еще является довольно неровным. Было бы лучше повторить процесс 1,000,000 раз, возможно, даже больше.39Эксперимент

Слайд 40Красная кривая показывает предельную форму распределения. Оно симметрично вокруг истинного значения,

что указывает на то, что метод оценивания объективен.
40
Эксперимент по методу

Монте-Карло

100 замеров

Красная кривая показывает предельную форму распределения. Оно симметрично вокруг истинного значения, что указывает на то, что метод оценивания

Слайд 41




Распределение нормальное, так как случайная составляющая коэффициента представляет собой взвешенную

линейную комбинацию значений остаточного члена в наблюдениях в образце. Мы продемонстрировали

это в предыдущем слайд-шоу.

41

Эксперимент по методу Монте-Карло

100 замеров

Распределение нормальное, так как случайная составляющая коэффициента представляет собой взвешенную линейную комбинацию значений остаточного члена в наблюдениях

Слайд 42




Мы предполагаем (Аксиома А.6), что остаточный член в каждом наблюдении

имеет нормальное распределение. Линейная комбинация нормально распределенных случайных величин имеет нормальное

распределение.

42

Эксперимент по методу Монте-Карло

100 замеров

Мы предполагаем (Аксиома А.6), что остаточный член в каждом наблюдении имеет нормальное распределение. Линейная комбинация нормально распределенных случайных

Похожие презентации

МУЗЕЙ БОЕВОЙ СЛАВЫ Номинация Лучший городской школьный музей Великой МУЗЕЙ БОЕВОЙ СЛАВЫ Номинация Лучший городской школьный музей Великой 306
ДИАЛОГ ПОКОЛЕНИЙ ДИАЛОГ ПОКОЛЕНИЙ 290
Геномика рака Геномика рака 328
Презентация песни Презентация песни "Башҡортостан тыуған ерем" 209
ЭКСТРЕМАЛЬНЫЕ СОСТОЯНИЯ ЭКСТРЕМАЛЬНЫЕ СОСТОЯНИЯ 292
Встречают по одёжке Встречают по одёжке 410
Матричные процессы Матричные процессы 209
Элементы физики в рамках современной образовательной деятельности в Элементы физики в рамках современной образовательной деятельности в 240
Путь от Солнца к сознанию Путь от Солнца к сознанию 201
Лимфаденопатия у детей Лимфаденопатия у детей 753
Соцветия Автор: Лабунец Ольга Юрьевна учитель биологии МОУ СОШ № 4 г. Мытищи Соцветия Автор: Лабунец Ольга Юрьевна учитель биологии МОУ СОШ № 4 г. Мытищи 156
ДОКАЗАТЕЛЬНАЯ МЕДИЦИНА И МЕДИЦИНСКАЯ РЕКЛАМА ДОКАЗАТЕЛЬНАЯ МЕДИЦИНА И МЕДИЦИНСКАЯ РЕКЛАМА 254
Lect-Ko-5-el-tok.ppt Lect-Ko-5-el-tok.ppt 265
KFUmniki-II-02 KFUmniki-II-02 198
Будем говорить понятно Будем говорить понятно 209
Литература Литература 418
Со здоровьем всё в порядке - спасибо утренней зарядке! советы Со здоровьем всё в порядке - спасибо утренней зарядке! советы 182
Дарья Донцова Дарья Донцова 213
Джордж Гордон Байрон Джордж Гордон Байрон 217
Эффективность алгоритмов Эффективность алгоритмов 437

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика