Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 Российский государственный университет нефти и газа им. И.М
Содержание
- 1. 1 Российский государственный университет нефти и газа им. И.М
- 2. Постановка задачи:вычислить интеграл видагде a и b
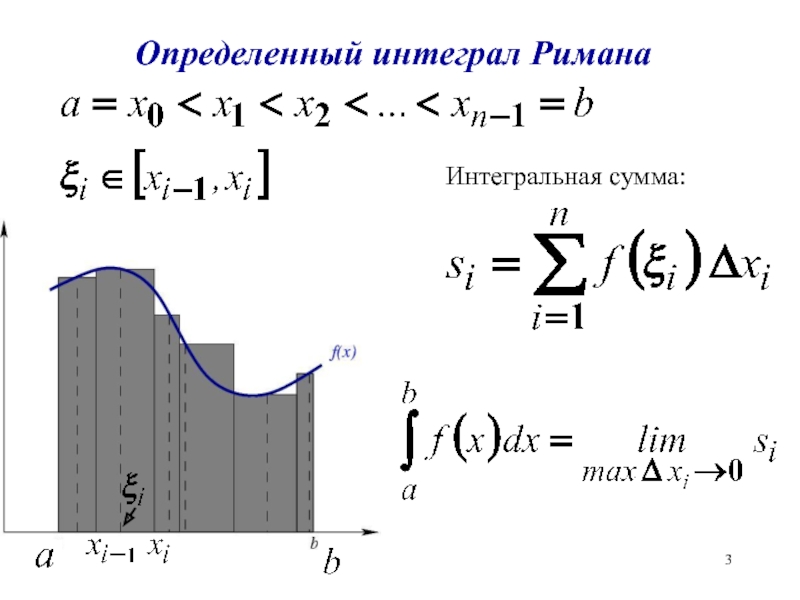
- 3. Определенный интеграл Римана
- 4. Вычисление определенных интеграловЗначение определенного интеграла можно трактовать как площадь криволинейной трапеции
- 5. методы численного интегрирования применяютЕсли: 1) вид функции
- 6. Квадратурные формулы Ньютона-КотесаЗамена f(x) – на
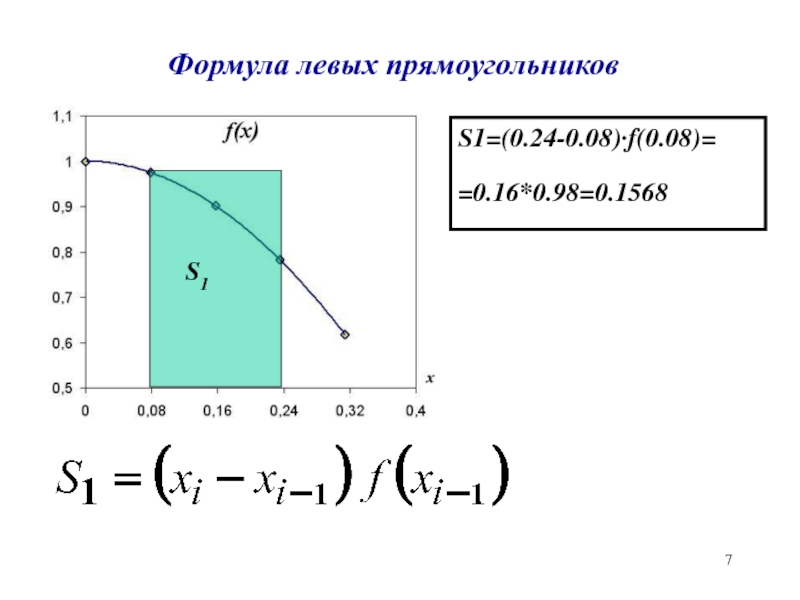
- 7. Формула левых прямоугольниковS1S1=(0.24-0.08)·f(0.08)==0.16*0.98=0.1568
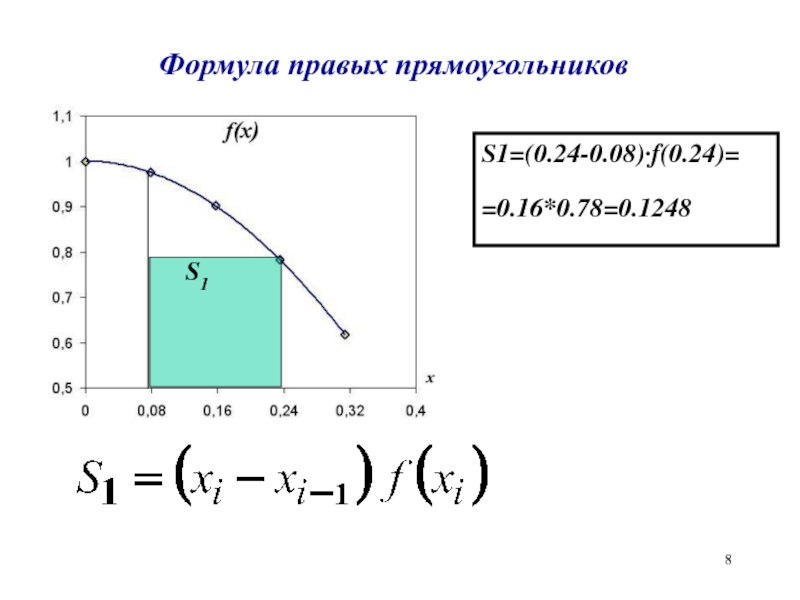
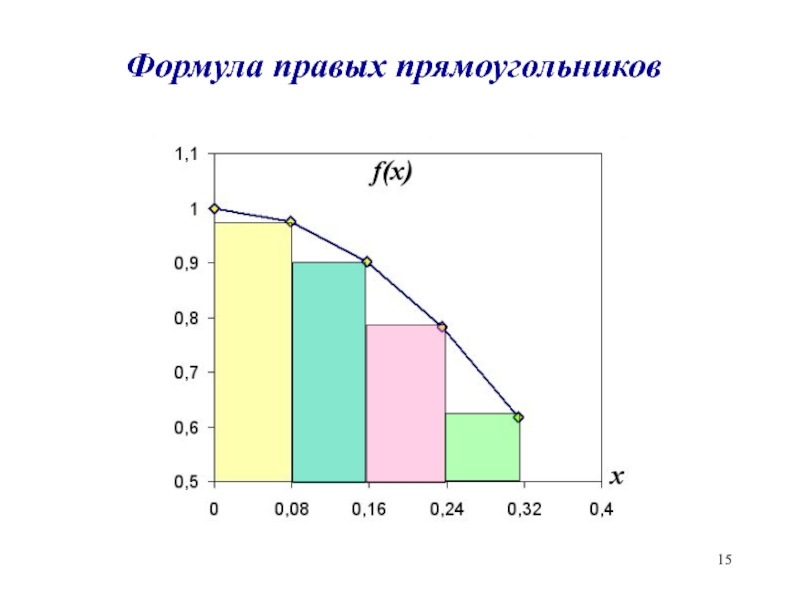
- 8. Формула правых прямоугольниковS1S1=(0.24-0.08)·f(0.24)==0.16*0.78=0.1248
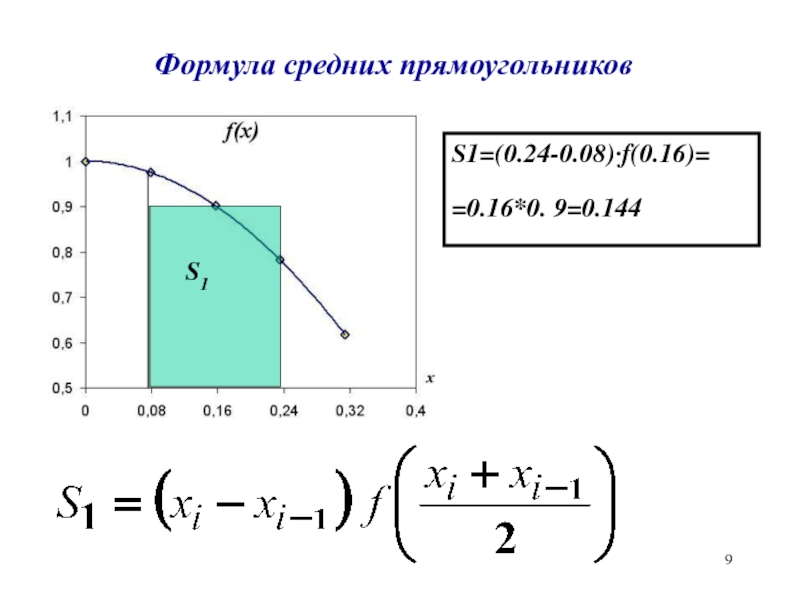
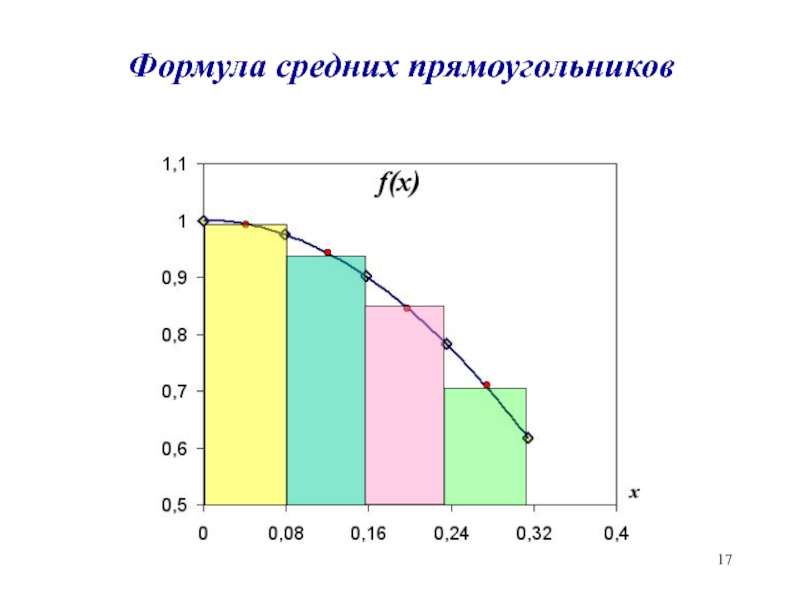
- 9. Формула средних прямоугольниковS1S1=(0.24-0.08)·f(0.16)==0.16*0. 9=0.144
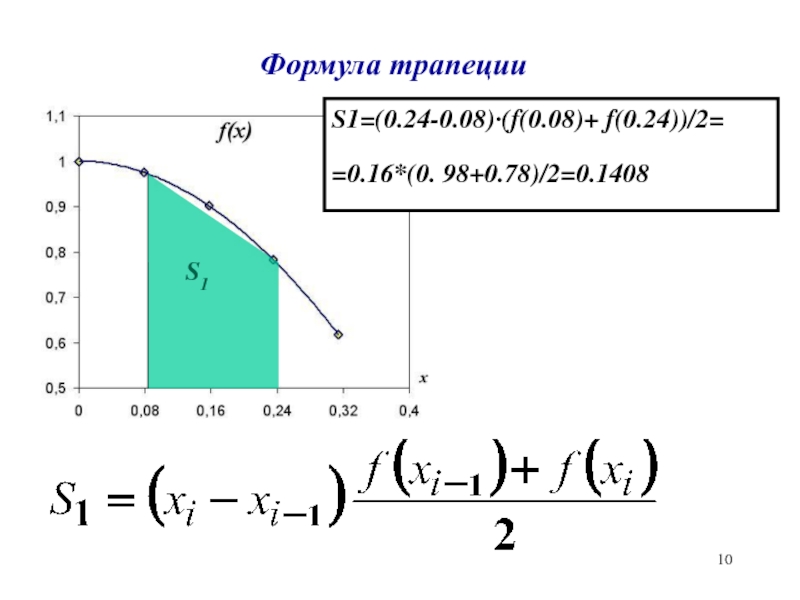
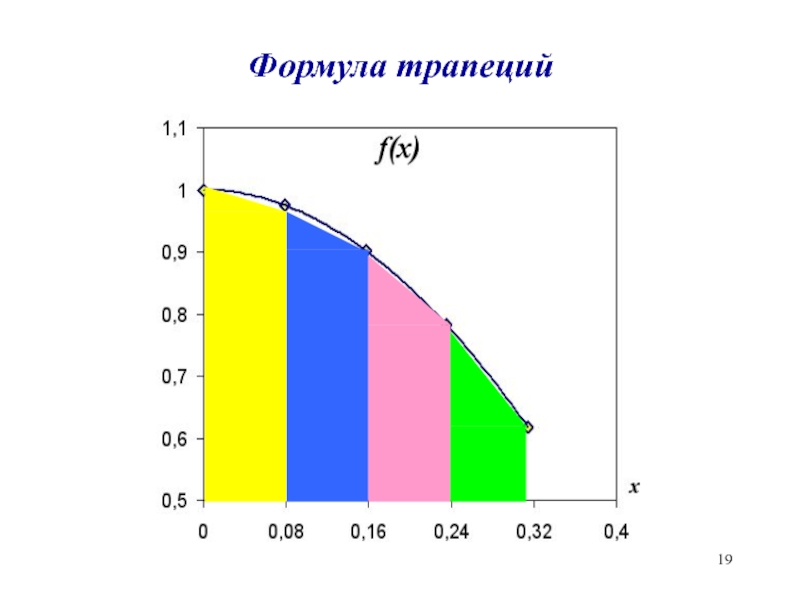
- 10. Формула трапецииS1S1=(0.24-0.08)·(f(0.08)+ f(0.24))/2==0.16*(0. 98+0.78)/2=0.1408
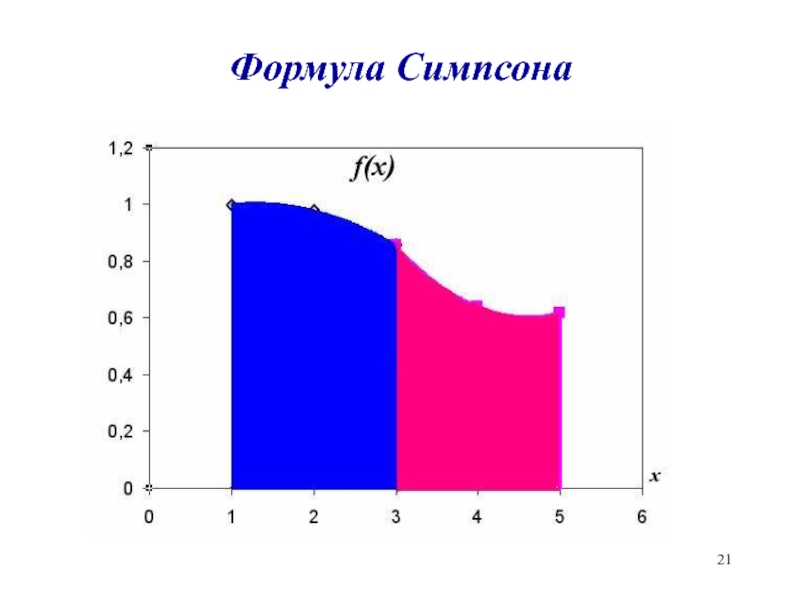
- 11. Формула Симпсона(трехточечная схема)h=0.08S1=0.08/3*f(0.08)+4f(0.16)+ f(0.24))==0.08/3*(0. 98+ 4*0.9+ 0.78)=0.1429
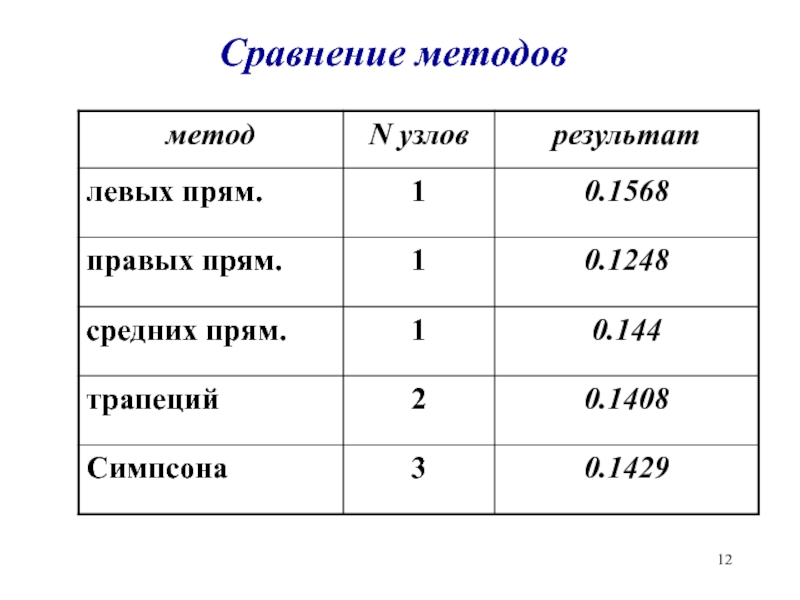
- 12. Сравнение методов
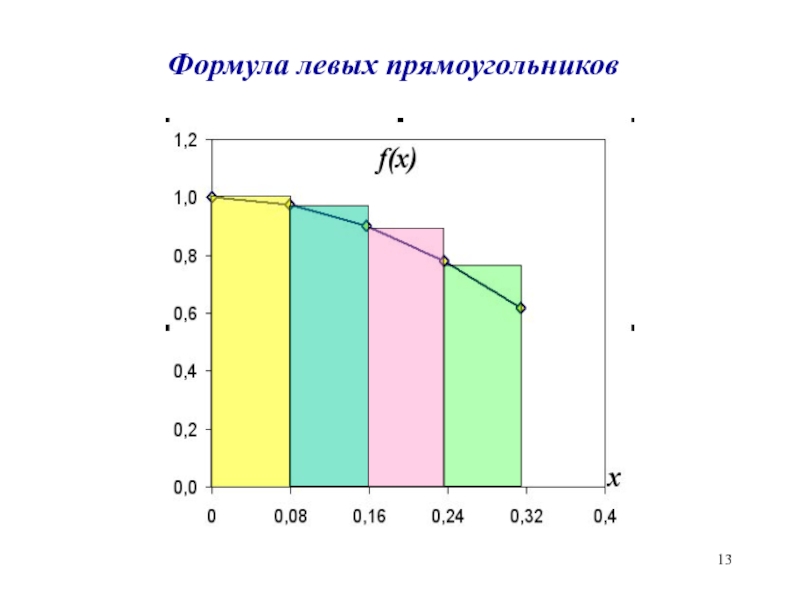
- 13. Формула левых прямоугольников
- 14. Метод левых прямоугольниковn – количество отрезков
- 15. Формула правых прямоугольников
- 16. Метод правых прямоугольников
- 17. Формула средних прямоугольников
- 18. Метод средних прямоугольниковn – количество отрезков
- 19. Формула трапеций
- 20. Метод трапеций
- 21. Формула Симпсона
- 22. Метод Симпсона
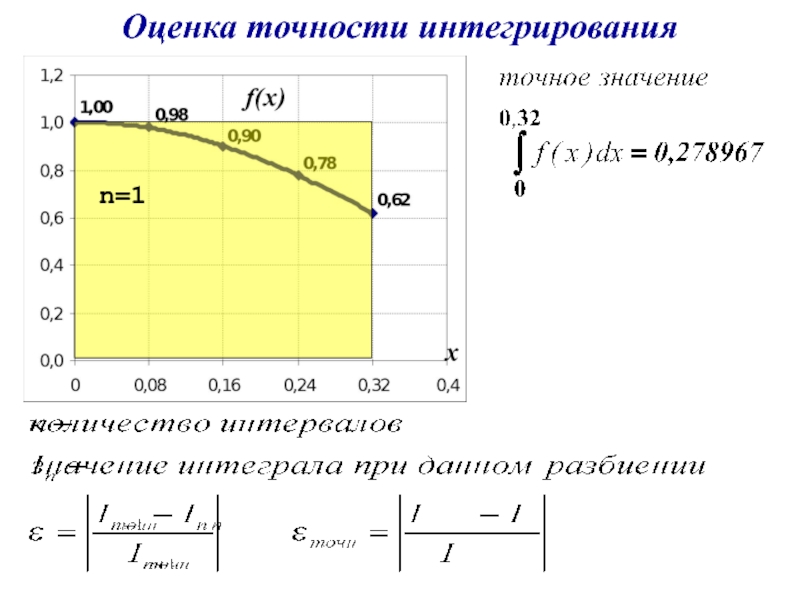
- 23. Оценка точности интегрирования
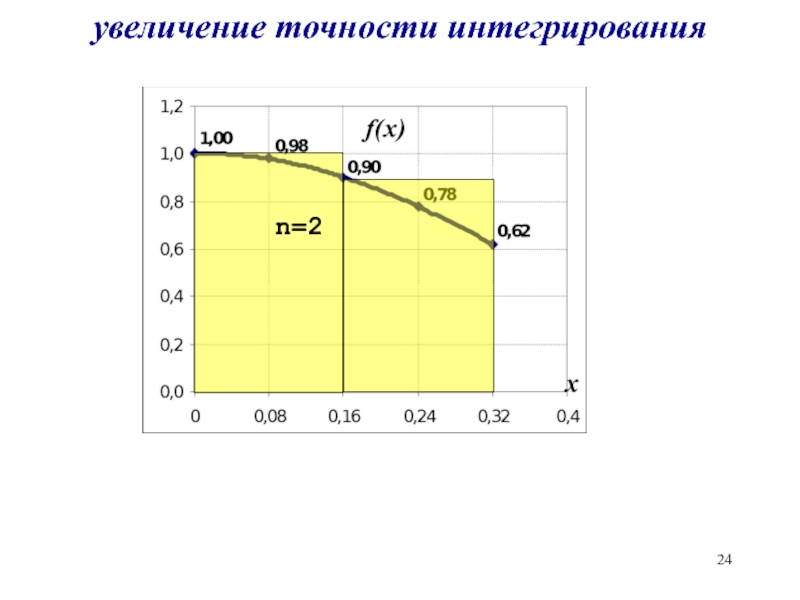
- 24. увеличение точности интегрирования
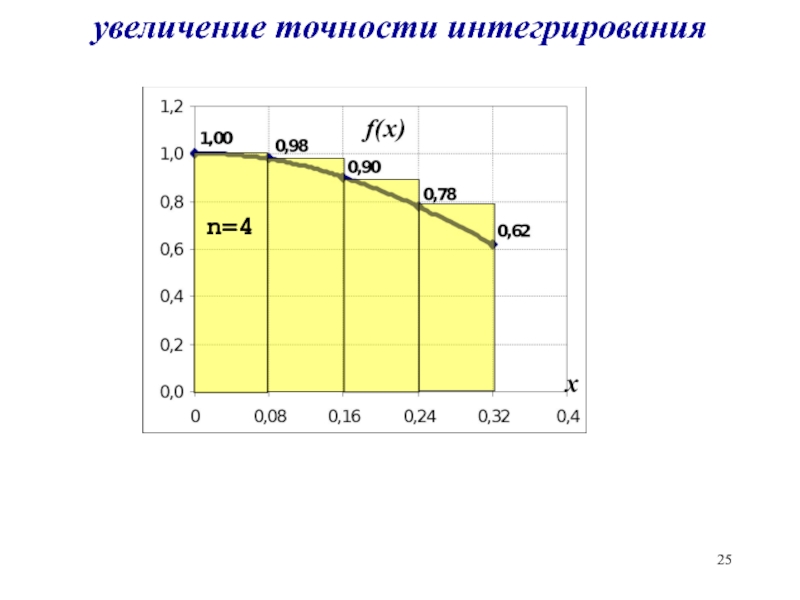
- 25. увеличение точности интегрирования
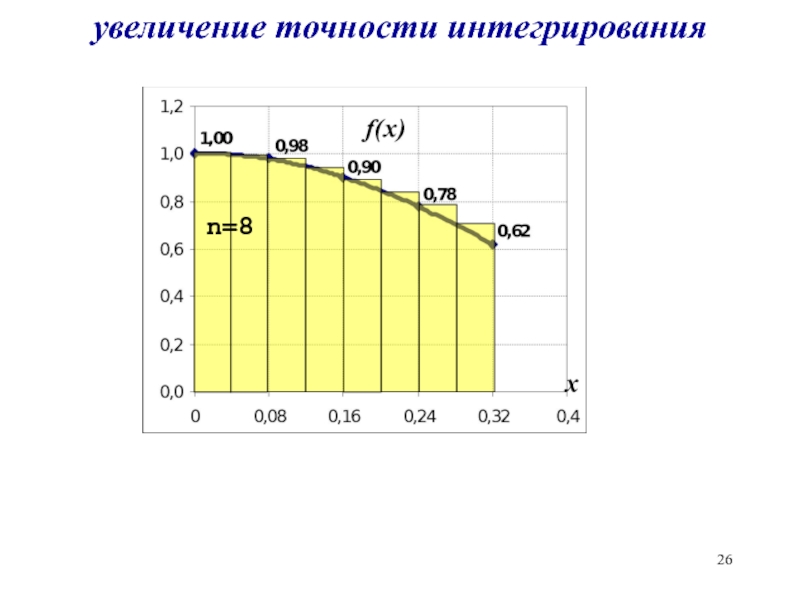
- 26. увеличение точности интегрирования
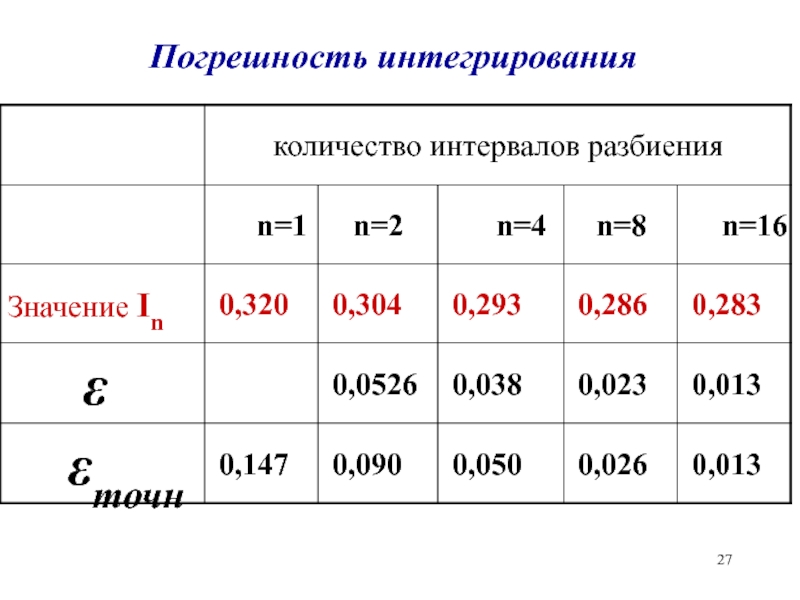
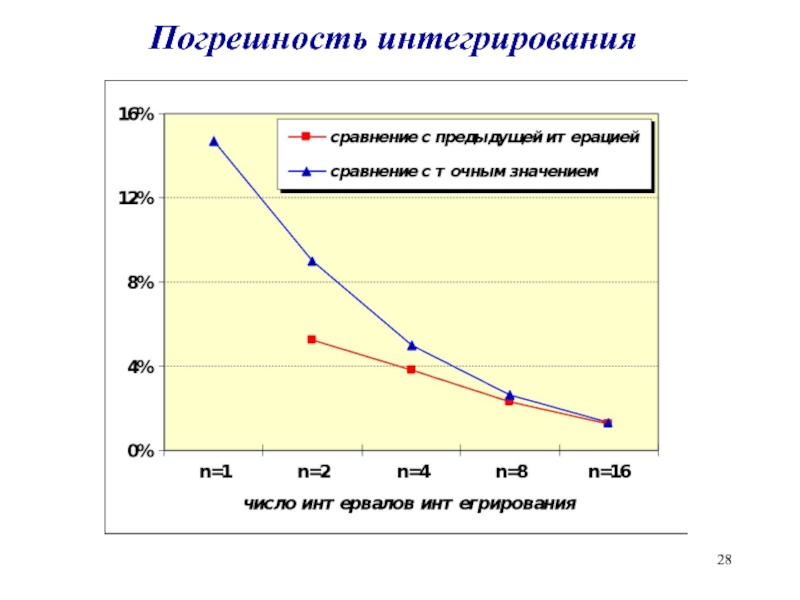
- 27. Погрешность интегрирования
- 28. Погрешность интегрирования
- 29. Символьное интегрирование в среде Matlabsyms xf=sym(‘x/(4+x^2’)s=int(f,x) –
- 30. Численное интегрирование в среде Matlaba=0;b=1;s=int(‘x/(4+x^2’,a,b) где s – численное значение интегралаa, b – пределы интегрирования
- 31. Численное интегрирование в среде MatlabМетод трапеций:s=trapz(x,y) –
- 32. Численное интегрирование в среде MatlabМетод Симпсона:[Q,FCNT]=quad(FUN,A,B,TOL)Q –
- 33. Скачать презентанцию
Постановка задачи:вычислить интеграл видагде a и b – пределы интегрирования; f(x) – непрерывная функция на отрезке [a,b]
Слайды и текст этой презентации
Слайд 1Российский государственный университет нефти и газа
им. И.М. Губкина
Численное интегрирование
Кафедра
«Информатики»
Слайд 2Постановка задачи:
вычислить интеграл вида
где a и b – пределы интегрирования;
f(x) – непрерывная функция на отрезке [a,b]
Слайд 4Вычисление определенных интегралов
Значение определенного интеграла можно трактовать как площадь криволинейной
трапеции
Слайд 5методы численного интегрирования применяют
Если:
1) вид функции f(x) не допускает
непосредственного интегрирования;
2) значения функции f(x) заданы в виде таблицы
Основная
идея - замена подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. Слайд 6Квадратурные формулы
Ньютона-Котеса
Замена f(x) – на полином различных степеней.
f(x)=const - метод прямоугольников,
f(x)=kx+b - метод трапеций,
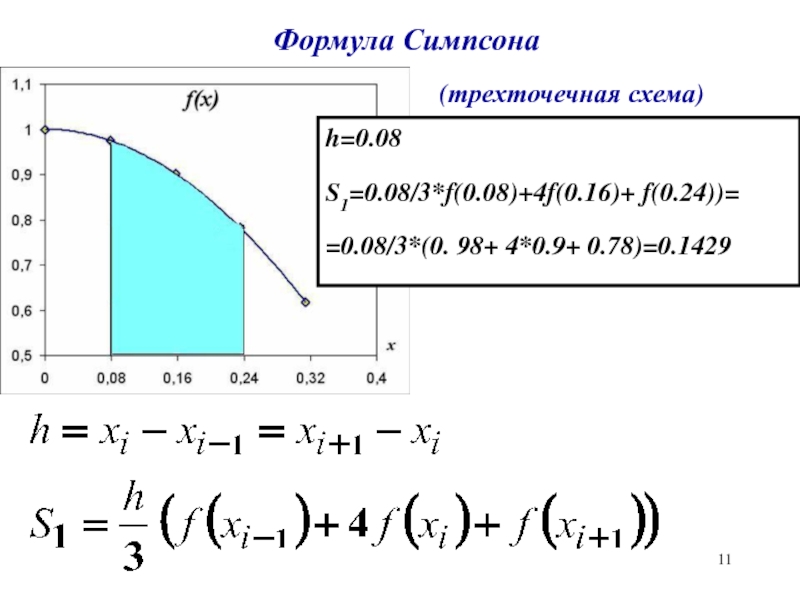
f(x)=ax2+bx+c - метод Симпсона. Слайд 11Формула Симпсона
(трехточечная схема)
h=0.08
S1=0.08/3*f(0.08)+4f(0.16)+ f(0.24))=
=0.08/3*(0. 98+ 4*0.9+ 0.78)=0.1429
Слайд 29Символьное интегрирование в среде Matlab
syms x
f=sym(‘x/(4+x^2’)
s=int(f,x) – функция вычисляющая значение
интеграла, где
s –
символьное значение интегралаf –подынтегральная функция.
Слайд 30Численное интегрирование в среде Matlab
a=0;
b=1;
s=int(‘x/(4+x^2’,a,b)
где
s – численное значение
интеграла
a, b – пределы интегрирования
Слайд 31Численное интегрирование в среде Matlab
Метод трапеций:
s=trapz(x,y)
– функция вычисляющая значение
интеграла методом трапеций, где
s – численное значение интеграла
x –
вектор значений аргументаy – вектор значений подынтегральной функции.
Слайд 32Численное интегрирование в среде Matlab
Метод Симпсона:
[Q,FCNT]=quad(FUN,A,B,TOL)
Q – значение интеграла по
методу Симпсона;
FCNT – Количество узлов при заданной точности;
FUN – подынтегральная
функция;A,B – пределы интегрирования;
TOL – точность вычислений, если не указывать, то принимается равной 10-6

![1
Российский государственный университет нефти и газа им. И.М Постановка задачи:вычислить интеграл видагде a и b – пределы интегрирования; f(x) Постановка задачи:вычислить интеграл видагде a и b – пределы интегрирования; f(x) – непрерывная функция на отрезке [a,b]](/img/tmb/4/332497/22923b28d3771961b527f892c40765b9-800x.jpg)











![1
Российский государственный университет нефти и газа им. И.М Численное интегрирование в среде MatlabМетод Симпсона:[Q,FCNT]=quad(FUN,A,B,TOL)Q – значение интеграла по методу Численное интегрирование в среде MatlabМетод Симпсона:[Q,FCNT]=quad(FUN,A,B,TOL)Q – значение интеграла по методу Симпсона;FCNT – Количество узлов при заданной](/img/thumbs/a3a433d8b2a81036d5454ae57998987b-800x.jpg)



















