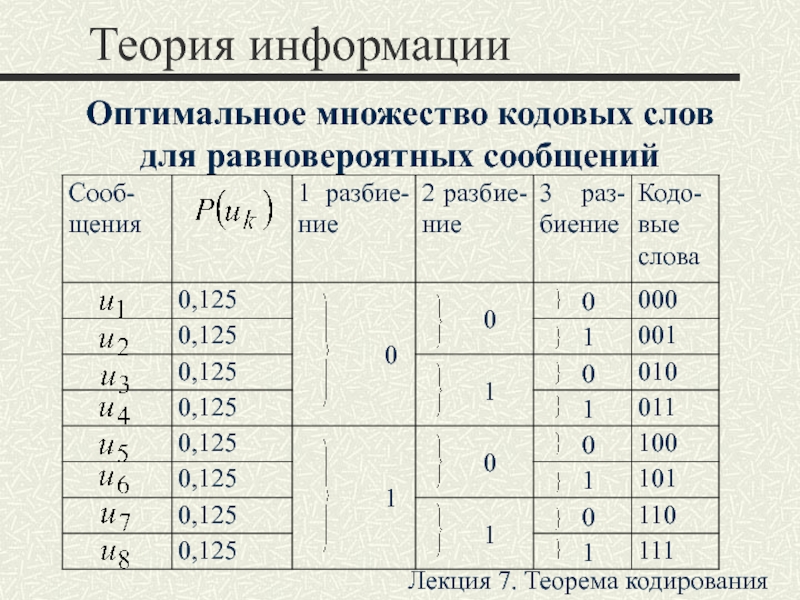
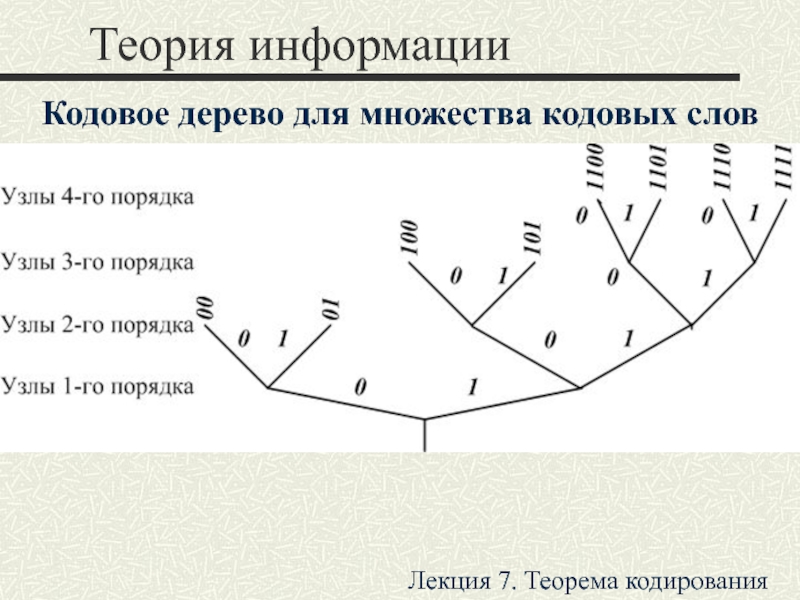
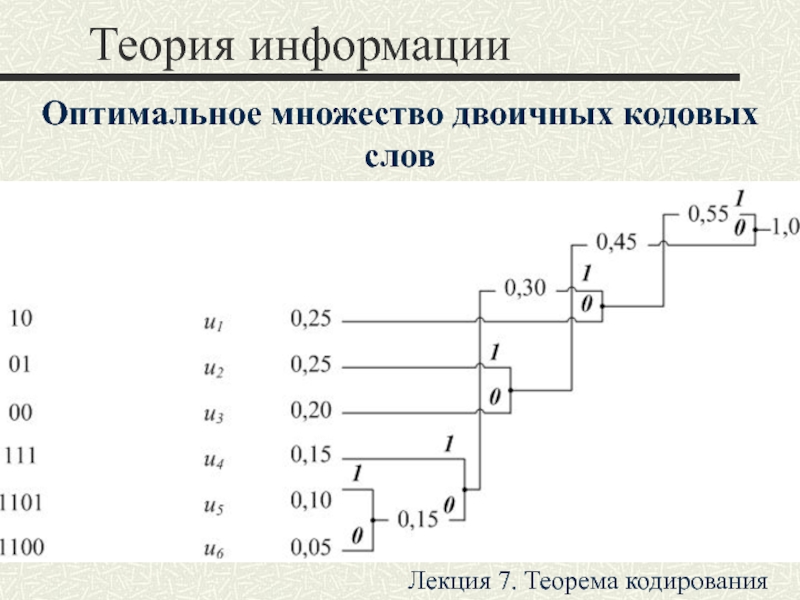
символов, принадлежащих заданному алфавиту.
Цель − конструирование последовательностей символов, минимизирующих среднее
число символов, приходящихся на одно сообщение по ансамблю статистически независимых сообщений.Лекция 7. Теорема кодирования