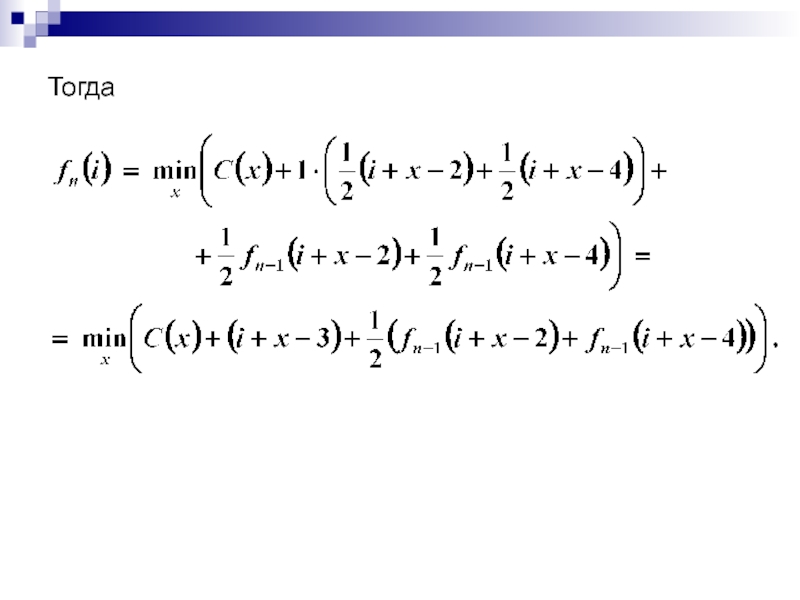Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
5. Примеры стохастических моделей динамического программирования
Содержание
- 1. 5. Примеры стохастических моделей динамического программирования
- 2. Рассмотренные ранее оптимизационные модели: для практической реализации
- 3. Использование анализа на чувствительность решения, полученного
- 4. Построение модели, содержащей фактор неопределенности в
- 5. Сложности, связанные с использованием вероятностных моделей (по
- 6. Общий подход: в стохастических динамических моделях, предназначенных для
- 7. Пример.Пусть Rt – доход, получаемый, согласно динамической
- 8. Примем как постулат: целевой функцией оптимизационной задачи
- 9. Замечание. Использование в оптимизационной модели вместо случайным образом
- 10. Пример (стохастический аналог рассмотренной ранее детерминированной задачи).
- 11. Формализация:при ограничениях для всех j yj =
- 12. Ранее было введено обозначение: gj(n) – прибыль, получаемая
- 13. В этих построениях предполагалось, что значение прибыли
- 14. Введем обозначения: rj(d | y) – значение прибыли,
- 15. Математическое ожидание (среднее значение) прибыли за счет
- 16. Элементарная модель управления запасамиПример. Фирма «Надежный поставщик». Фирма
- 17. Общие затраты, связанные с производством и хранением,
- 18. При постоянном для всех отрезков уровне спроса
- 19. Предположим теперь, что уровень спроса D –
- 20. Предположим:в конце планового периода складские запасы не
- 21. Еще одно ограничение: наименьшее значение спроса равно 2
- 22. Важно: переменная, характеризующая состояние в стохастической
- 23. Рекуррентные соотношенияпри n = 1 (затраты на производство
- 24. Пусть n = 2, 3, …При заданном
- 25. Тогда
- 26. Итог:где i = 0, 1, 2,
- 27. Главное отличие рекуррентного соотношения (5.7) (для детерминированной
- 28. n = 1. С(0) =0, С(1) = 15,
- 29. n = 2. х – неотрицательные целые, удовлетворяющие
- 30. В каждой клетке: С(х) +
- 31. n = 3. х – неотрицательные целые, удовлетворяющие
- 32. В каждой клетке: С(х) +
- 33. Можно доказать, что для любого n ≥
- 34. Сопоставление результатов, полученных для детерминированной и стохастической
- 35. Задача инвестированияПример.Требуется определить оптимальную инвестиционную политику в
- 36. Примем: оптимальной является стратегия,
- 37. Предположим, что в течение i-го года сохранялось
- 38. Поэтому
- 39. При i = Nи
- 40. При М(rN) ≤ 0
- 41. Итог:
- 42. Можно показать:
- 43. Числовой пример.Первоначальная сумма (возможный объем инвестиции в
- 44. i = N = 4. М(r4) =
- 45. i = N–1 = 3. Из (5.9)
- 46. i = 2. Из (5.9)
- 47. i = 1. Из (5.9)
- 48. Оптимальная инвестиционная политика: первый год: инвестировать все 10
- 49. Стохастическая модель восстановления
- 50. Задача с конечным плановым периодом.Обозначим: fn – интегральные
- 51. Задача с бесконечным плановым периодом.Соответствующее предельное соотношение
- 52. Важный частный случай модели восстановления –
- 53. Введем обозначения: k – отрезок времени, на котором
- 54. Примем: оптимальной является стратегия,
- 55. Для задачи с конечным плановым периодом –
- 56. Пояснение к (5.16):
- 57. При n < N минимизация, как и
- 58. Для задачи с бесконечным плановым периодом обобщение (5.12)
- 59. f – математическое ожидание дисконтированных затрат при неограниченном плановом периоде в случае, когда реализуется оптимальная стратегия.
- 60. При α = 1 формула (5.18) неприменима. Заменим
- 61. Пояснение к (5.19):
- 62. Величина M(j | k) определяет ожидаемое число
- 63. Скачать презентанцию
Рассмотренные ранее оптимизационные модели: для практической реализации необходимо полностью детерминированное представление всех исходных данных.В реальных условиях часто присутствует неопределенность (неизвестные числовые значения по крайней мере некоторых из параметров модели).
Слайды и текст этой презентации
Слайд 2Рассмотренные ранее оптимизационные модели:
для практической реализации необходимо полностью детерминированное
представление всех исходных данных.
числовые значения по крайней мере некоторых из параметров модели).
Слайд 3 Использование анализа на чувствительность решения, полученного для детерминированной модели.
Сначала с помощью детерминированной модели определяется оптимальная программа для ряда
вероятных значений недетерминированного параметра. Если оптимальное решение нечувствительно к этому параметру, то можно утверждать: используемая модель адекватно учитывает элемент неопределенности.
Если решение обладает сильной чувствительностью к вариациям параметра, то необходим дополнительный анализ (оценка вероятностей различных значений параметра, принятие решения с учетом риска).
Основные подходы к учету неопределенности в задачах организационного управления
Слайд 4 Построение модели, содержащей фактор неопределенности в явном виде.
Учет и
анализ вероятностных характеристик в оптимизационных моделях рассматривается далее.
Будем предполагать:
любая
неопределенность характеризуется некоторым распределением вероятностей различных возможных событий (исходов).
Слайд 5Сложности, связанные с использованием вероятностных моделей (по сравнению с детерминированными):
трудности
концептуального характера (например, определение критерия оптимальности);
трудности технического характера, обусловленные особенностями
математического аппарата, используемого при решении стохастических задач оптимизации;большое число исходных данных, необходимых для нахождения распределения вероятностей.
Слайд 6Общий подход:
в стохастических динамических моделях, предназначенных для оптимизации некоторой последовательности
значений дохода (эффекта), целевая функция представляет собой ожидаемое значение (математическое
ожидание, среднее значение) ее детерминированного аналога.
Слайд 7Пример.
Пусть Rt – доход, получаемый, согласно динамической
модели, на отрезке t,
R – приведенный (с учетом
дисконтирования) суммарный доход.При наличии элементов неопределенности любая стратегия формирования управляющих решений на протяжении планового периода порождает совместное распределение вероятностей для элементов последовательности {R1, R2, R3, … }.
Слайд 8Примем как постулат:
целевой функцией оптимизационной задачи является математическое ожидание
суммарного приведенного потока доходов
M(R) = M(R1 + α∙R2 + α2∙R3
+ … ),где α – коэффициент дисконтирования, 0 ≤ α < 1.
По свойствам математического ожидания
M(R) = M(R1) + α∙М(R2) + α2∙М(R3) + …
Предполагается, что R имеет конечное математическое ожидание
Слайд 9Замечание.
Использование в оптимизационной модели вместо случайным образом изменяющихся коэффициентов их
ожидаемых значений, как правило, является недопустимым. Это может привести к
серьезным ошибкам.Причина:
для нелинейной функции f(х1, х2, … , хn) случайных переменных х1, х2, … , хn
M(f(х1, х2, … , хn) ) ≠ f(M(х1), … , M(хn)).
Слайд 10Пример (стохастический аналог рассмотренной ранее детерминированной задачи).
Владелец торговой фирмы
должен распределить имеющийся у него недельный запас в количестве N
единиц продукции по s магазинам.Из опыта известно, что если направить yj единиц в магазин j, то прибыль составит Rj(уj).
Владелец фирмы стремится найти такое распределение имеющейся в наличии продукции по магазинам, чтобы суммарная прибыль была максимальной.
Задача распределения ресурсов
Слайд 11Формализация:
при ограничениях
для всех j yj = 0, 1, 2,
… , N (5.3)
(только целочисленные значения).
Слайд 12Ранее было введено обозначение:
gj(n) – прибыль, получаемая при оптимальном
распределении n ед. продукции по
магазинам 1, 2, ... , j.Решение может быть получено с помощью рекуррентного соотношения
где n = 0, 1, 2, … , N,
максимум берется по yj = 0, 1, … , n.
Слайд 13В этих построениях предполагалось, что значение прибыли Rj(уj) известно заранее
и определяется однозначно.
Предположим теперь:
прибыль зависит не только от уj,
но и от фактического спроса на товар в j-м магазине, причем объем спроса в j-м магазине – случайная величина, которая не зависит от уj;
ее значение становится известным только после того, как выбраны значения всех управляемых переменных уj.
Слайд 14Введем обозначения:
rj(d | y) – значение прибыли, получаемой магазином j
в случае, если фактический уровень спроса равняется d, а объем
поставок в этот магазин составляет у ед.;рj(d) – вероятность того, что уровень спроса для магазина j равен d.
где rj – прибыль от каждой единицы товара, проданной в j-м магазине.
Слайд 15Математическое ожидание (среднее значение) прибыли за счет поставок в j-й
магазин уj ед. товара (обозначим Rj(уj)) равно
где суммирование производится по
всем возможным значениям уровня спроса.Тогда оптимальное решение стохастической задачи может быть найдено как решение задачи (5.1) – (5.3), в которой Rj(уj) определяется в соответствии с (5.6).
(5.6)
Задача сведена к детерминированной модели
Слайд 16Элементарная модель управления запасами
Пример. Фирма «Надежный поставщик».
Фирма должна разработать календарную
программу выпуска некоторого вида изделий на плановый период, состоящий из
N отрезков, при которой общая сумма затрат на производство и содержание запасов минимальна (при условии полного и своевременного удовлетворения спроса на продукцию).Ограничения (для всех отрезков):
объем производства x ≤ 5,
уровень запасов на конец отрезка j ≤ 4.
Слайд 17Общие затраты, связанные с производством и хранением, равны
С(х, j)
=С(х) + h∙j ,
где
х = 0, 1, 2,
3, 4, 5, j = 0, 1, 2, 3, 4, С(0) =0, С(1) = 15, С(2) = 17, С(3) = 19,
С(4) = 21, С(5) = 23, h = 1
для всех отрезков планового периода.
Переменная состояния i – уровень запасов на начало отрезка.
Слайд 18При постоянном для всех отрезков уровне спроса D = 3
рекуррентное соотношение динамического программирования имело вид:
n = 2, 3, …
,где i = 0, 1, 2, 3, 4,
х – неотрицательные целые, удовлетворяющие условиям:
3 – i ≤ х ≤ min{ 5, 7 – i },
х ≤ 3∙n – i .
Слайд 19Предположим теперь, что уровень спроса D – случайная величина, которая
может принимать одно из двух равновероятных значений (на каждом отрезке
независимо от других отрезков):так что M(D) = 2∙0,5 + 4∙0,5 = 3.
Слайд 20Предположим:
в конце планового периода складские запасы не принимаются во внимание
и не приводят к затратам на хранение (в детерминированной модели
уровень запасов на конец планового периода полагался равным нулю).объем производства должен быть достаточен для того, чтобы запасы никогда не истощались (не принимали отрицательных значений)
ограничение: i + x ≥ 4.
Слайд 21Еще одно ограничение:
наименьшее значение спроса равно 2 ед.,
уровень запасов в
конце отрезка не может превышать 4 ед.,
i + x ≤ 6.Итого, имеем ограничения на х:
4 – i ≤ x ≤ min {5, 6 – i }.
Слайд 22Важно: переменная, характеризующая состояние в стохастической модели, – это
по-прежнему уровень запасов на начало отрезка.
Пояснение:
т. к. значения
спроса на каждом отрезке независимы от значений спроса на остальных отрезках, то единственным показателем состояния системы, связанным с ее прошлым состоянием, является имеющийся в наличии объем запасов.
Слайд 23Рекуррентные соотношения
при n = 1
(затраты на производство такого количества продукции,
чтобы с учетом имеющихся запасов мог быть удовлетворен максимально возможный
уровень спроса).
Слайд 24Пусть n = 2, 3, …
При заданном уровне запасов i
ожидаемые затраты при реализации оптимальной стратегии включают
затраты С(х) на производство
х ед. продукции;ожидаемые затраты на хранение (по состоянию на конец отрезка, т. е. в объеме i + х – D);
затраты, которые будут иметь место в последующие отрезки планового периода:
M(fn–1(i + х – D) ).
Слайд 26Итог:
где i = 0, 1, 2, 3, 4,
х – неотрицательные целые, удовлетворяющие условию:
4
– i ≤ x ≤ min {5, 6 – i }.
Слайд 27Главное отличие рекуррентного соотношения (5.7) (для детерминированной модели), от соотношения
(5.8) для стохастической задачи:
в последнем случае необходимо произвести дополнительные
вычисления, связанные с определением M(fn–1(i + х – D) ).Далее – вычисления для рассматриваемого примера.
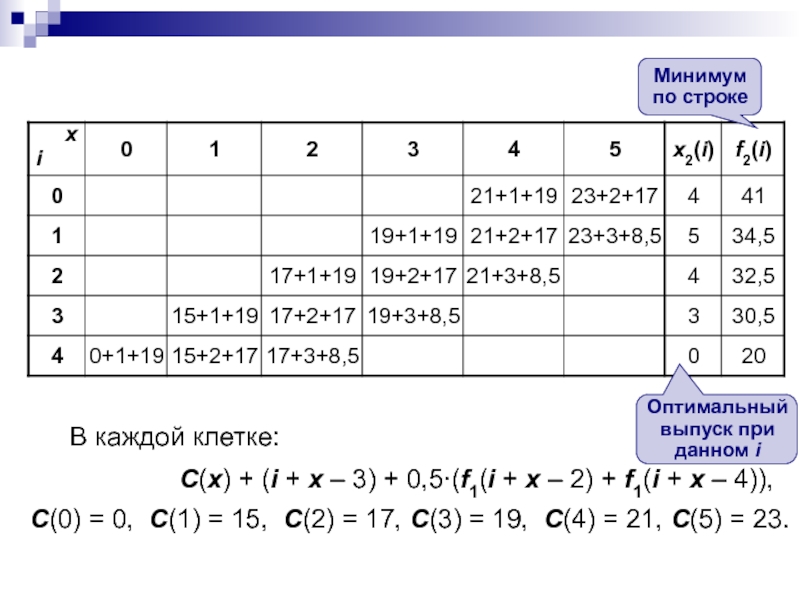
Слайд 30
В каждой клетке:
С(х) + (i + x
– 3) + 0,5∙(f1(i + x – 2) + f1(i
+ x – 4)),С(0) = 0, С(1) = 15, С(2) = 17, С(3) = 19, С(4) = 21, С(5) = 23.
Минимум по строке
Оптимальный выпуск при данном i
Слайд 32
В каждой клетке:
С(х) + (i + x
– 3) + 0,5∙(f2(i + x – 2) + f2(i
+ x – 4)),С(0) = 0, С(1) = 15, С(2) = 17, С(3) = 19, С(4) = 21, С(5) = 23.
Минимум по строке
Оптимальный выпуск при данном i
Слайд 33Можно доказать, что для любого n ≥ 3 оптимальной будет
одна и та же производственная программа.
Значения fn(i) и хn(i) для
n ≤ 5 и n = ∞:
Слайд 34Сопоставление результатов, полученных для детерминированной и стохастической модели:
При любом начальном
уровне запасов i и длительности оставшейся части планового периода n
ожидаемые затраты при оптимальной стратегии в случае случайного изменения уровня спроса будут выше оптимальных затрат при детерминированном спросе.При заданном i оптимальное значение хn(i) при стохастическом спросе никогда не убывает с ростом n (в отличие от детерминированной модели).
Оптимальная стратегия для планового периода большой протяженности была получена
в случае стохастического спроса при n = 3,
в детерминированной ситуации – при n = 18.
Слайд 35Задача инвестирования
Пример.
Требуется определить оптимальную инвестиционную политику в течение N лет
при следующих условиях:
первоначальный объем инвестиций составляет k1 д. е.;
доход, полученный
в течение одного года, может быть снова инвестирован (полностью или частично) в начале следующего года;величина прибыли r (доля от вложенной суммы) зависит от условий рынка и имеет вероятностный характер:
Слайд 36Примем: оптимальной является стратегия, максимизирующая
ожидаемое значение (математическое ожидание) общей суммы
поступления денежных средств за N лет.Ведем обозначения:
ki – сумма, доступная для инвестирования в начале i-го года;
xi – сумма реальной инвестиции в начале i-го года (xi ≤ ki);
fi(ki) – максимальная ожидаемая сумма денежных поступлений, полученная в течение календарных лет: i, i+1, … , N при условии, что в начале i-го года имеется сумма ki.
Слайд 37Предположим, что в течение i-го года сохранялось состояние рынка с
номером j (соответствует величине прибыли, равной rij).
Тогда
Ожидаемая сумма денежных поступлений,
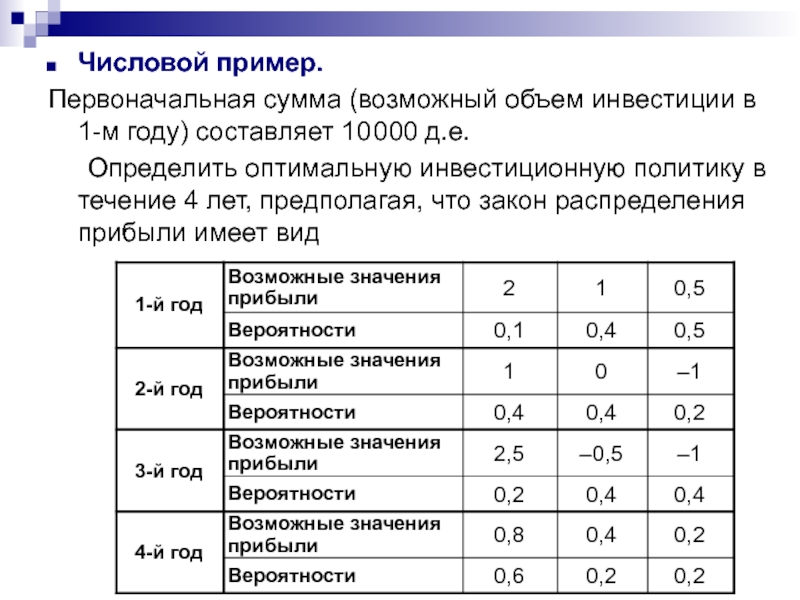
полученная за годы i+1, … , N, при условии, что в эти годы выбиралась оптимальная стратегия, составит 
Слайд 43Числовой пример.
Первоначальная сумма (возможный объем инвестиции в 1-м году) составляет
10 000 д.е.
Определить оптимальную инвестиционную политику в течение 4
лет, предполагая, что закон распределения прибыли имеет вид
Слайд 44i = N = 4.
М(r4) = 0,8∙0,6 + 0,4∙0,2
+ 0,2∙0,2 = 0,6 ≥ 0
f4(k4) = (1 + 0,6)∙k4
=1,6k4,x4 = k4.
Слайд 48Оптимальная инвестиционная политика:
первый год: инвестировать все 10 000 д. е.;
второй
год: инвестировать всю накопленную сумму;
третий год: воздержаться от инвестиций;
четвертый год:
инвестировать всю накопленную сумму.Ожидаемые накопления к концу четвертого года составят
3,232∙ k1 = 3,232∙10 000 = 32 320 д. е.
Слайд 49Стохастическая модель восстановления
(на примере задачи замены оборудования)
Ранее рассмотрена детерминированная задача:
момент восстановления
можно выбирать из N альтернативных вариантов, которым присвоены индексы k = 1, 2, . . ., N; если вариант k выбран в момент восстановления t, то следующий момент восстановления наступит на отрезке (t + k).
Было введено обозначение:
Rk – затраты варианта k при их оценке в начале его периода восстановления.
Цель оптимизации – определить стратегию, минимизирующую затраты.
Слайд 50Задача с конечным плановым периодом.
Обозначим:
fn – интегральные дисконтированные (приведенные)
затраты для оптимальной стратегии восстановления,
при которой один из альтернативных вариантов должен быть выбран за n отрезков до конца планового периода.Оптимальная стратегия может быть выбрана с помощью рекуррентного соотношения
при n ≥ N
при n < N минимум отыскивается при k = 1, 2, ... , n.
Слайд 51Задача с бесконечным плановым периодом.
Соответствующее предельное соотношение имеет вид
откуда
После замены
f на эквивалентный средний доход g
= (1 – α)∙f :
Слайд 52Важный частный случай модели восстановления – модель замены оборудования.
Детерминированный вариант:
k характеризует продолжительность времени, в течение которого оборудование
функционирует нормально (остается пригодным для эксплуатации). Стохастический вариант:
допускается, что оборудование может выйти из строя (например, в результате поломки) до запланированного момента замены (до наступления отрезка t + k).
Если на отрезке t планируется замена устройств, прослуживших срок k, а устройство выходит из строя на отрезке t + j, где j < k, то замена оборудования должна состояться на отрезке t + j + 1.
Слайд 53Введем обозначения:
k – отрезок времени, на котором планируется произвести замену
оборудования;
рj – вероятность того, что первая поломка оборудования произойдет в
течение j-го отрезка;rj – стоимость эксплуатации оборудования в течение j-го отрезка, если это устройство останется исправным;
(rj + sj) – стоимость эксплуатации оборудования, если поломка произойдет в течение j-го отрезка (j < k, sj > 0).
rj включает в себя первоначальную
стоимость оборудования;
sj можно рассматривать как ущерб от
преждевременной поломки оборудования
Слайд 54Примем: оптимальной является стратегия,
минимизирующая математическое ожидание
дисконтированных затрат.Ожидаемые дисконтированные затраты при выборе k-го варианта включают в себя средние дисконтированные затраты в очередной и во все последующие моменты восстановления
в случае, если оборудование выйдет из строя раньше запланированного отрезка;
в случае, если оборудование не выйдет из строя до запланированного периода восстановления;
ожидаемые эксплуатационные затраты в период между текущим и очередным моментами восстановления.
Слайд 57При n < N минимизация, как и ранее, проводится при
k = 1, 2, ... , n.
При
pj = 0, j = 1, 2, …, k–1, задача сводится к детерминированному варианту, а соотношение (5.15) – к (5.11), где
Слайд 58Для задачи с бесконечным плановым периодом
обобщение (5.12) при 0 ≤
α < 1 имеет вид:
где
среднее значение коэффициента
дисконтирования,
Rk определяется по формуле
(5.16).
Слайд 59f – математическое ожидание дисконтированных затрат при неограниченном плановом периоде
в случае, когда реализуется оптимальная стратегия.
Слайд 60При α = 1 формула (5.18) неприменима.
Заменим f на эквивалентный
средний доход g = (1
– α)∙f :где Rk определяется по формуле (5.16) при α = 1,
среднее значение сроков замены оборудования.
Слайд 62Величина M(j | k) определяет ожидаемое число отрезков использования каждого
устройства при заданном планируемом сроке замены k.
Величину g можно интерпретировать
как минимальное значение отношения ожидаемых затрат в течение интервала времени между двумя последовательными моментами замены к математическому ожиданию длины этого интервала (минимальные ожидаемые затраты за один отрезок при неограниченном плановом периоде.).
