Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Introduction to Quantum mechanics
Содержание
- 1. Introduction to Quantum mechanics
- 2. Einstein’s special theory of relativity when dealing
- 3. As physicists sought new ways to solve
- 4. Blackbody Radiation and Planck’s HypothesisAn object at
- 5. Blackbody Radiation and Planck’s HypothesisThe following two
- 6. Blackbody Radiation and Planck’s Hypothesis2. The peak
- 7. Blackbody Radiation and Planck’s HypothesisTo describe the
- 8. Blackbody Radiation and Planck’s HypothesisIn 1900, Max
- 9. Blackbody Radiation and Planck’s Hypothesis• The oscillators
- 10. Blackbody Radiation and Planck’s HypothesisAn oscillator emits
- 11. Blackbody Radiation and Planck’s Hypothesis
- 12. The Photoelectric EffectBlackbody radiation was the first
- 13. The Photoelectric EffectΔVs is the stopping potential
- 14. The Photoelectric EffectIn Einstein’s model of the
- 15. The Photoelectric EffectRearranging the equation:cutoff wavelength λccutoff
- 16. The Photoelectric Effect
- 17. The Compton EffectBecause different electrons move at
- 18. The Compton Effect the Compton shift equationthe Compton wavelength of the electron
- 19. The Compton Effect
- 20. The Nature of Electromagnetic WavesPhenomena such as
- 21. The Nature of Electromagnetic WavesSome experiments can
- 22. The Wave Properties of ParticlesEvery large-scale observation
- 23. The Wave Properties of ParticlesFurthermore, in analogy
- 24. The Wave Properties of ParticlesThe Davisson–Germer ExperimentThe
- 25. The Wave Properties of ParticlesThe Davisson–Germer Experiment
- 26. The Wave Properties of ParticlesThe Davisson–Germer ExperimentShortly
- 27. The Wave Properties of ParticlesThe Electron MicroscopeA
- 28. A New Model: The Quantum ParticleBecause in
- 29. A New Model: The Quantum ParticleLet’s first
- 30. A New Model: The Quantum ParticleIf a
- 31. A New Model: The Quantum ParticleThe second
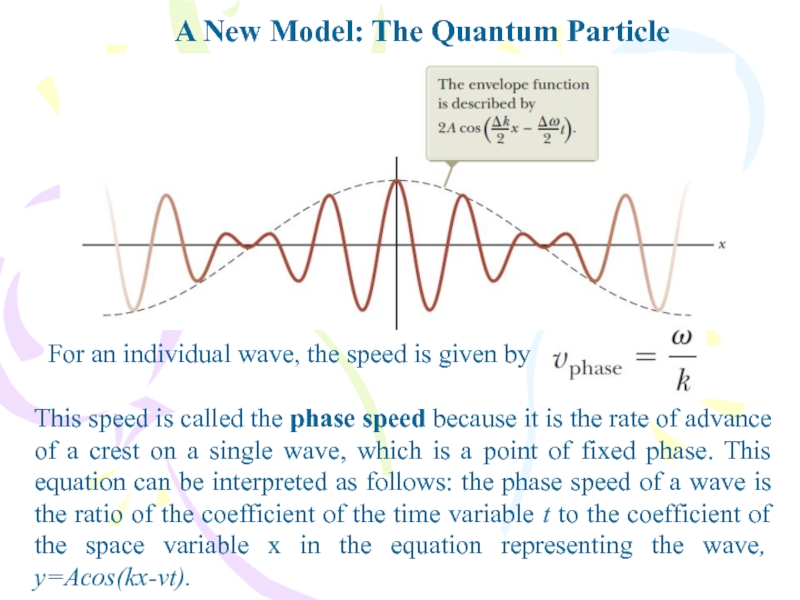
- 32. A New Model: The Quantum ParticleFor an
- 33. A New Model: The Quantum ParticleThe group
- 34. A New Model: The Quantum ParticleThe group
- 35. The Double-Slit Experiment RevisitedThe dual nature of
- 36. The Double-Slit Experiment Revisited
- 37. The Uncertainty PrincipleWhenever one measures the position
- 38. The Uncertainty PrincipleIf a measurement of the
- 39. The Uncertainty PrincipleThe form of the uncertainty
- 40. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Einstein’s special theory of relativity when dealing with particle speeds
comparable to the speed of light. As the 20th century
progressed, many experimental and theoretical problems were resolved by the special theory of relativity. For many other problems, however, neither relativity nor classical physics could provide a theoretical answer. Attempts to apply the laws of classical physics to explain the behavior of matter on the atomic scale were consistently unsuccessful. For example, the emission of discrete wavelengths of light from atoms in a hightemperature gas could not be explained within the framework of classical physics.Слайд 3As physicists sought new ways to solve these puzzles, another
revolution took place in physics between 1900 and 1930. A
new theory called quantum mechanics was highly successful in explaining the behavior of particles of microscopic size. Like the special theory of relativity, the quantum theory requires a modification of our ideas concerning the physical world.The first explanation of a phenomenon using quantum theory was introduced by Max Planck. Many subsequent mathematical developments and interpretations were made by a number of distinguished physicists, including Einstein, Bohr, de Broglie, Schrцdinger, and Heisenberg. Despite the great success of the quantum theory, Einstein frequently played the role of its critic, especially with regard to the manner in which the theory was interpreted.
Because an extensive study of quantum theory is beyond the scope of this book, this chapter is simply an introduction to its underlying principles.
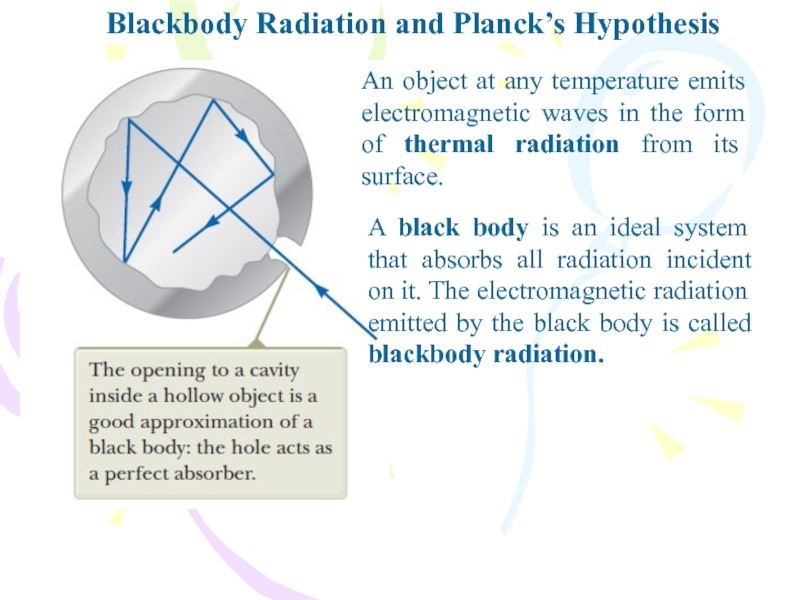
Слайд 4Blackbody Radiation and Planck’s Hypothesis
An object at any temperature emits
electromagnetic waves in the form of thermal radiation from its
surface.A black body is an ideal system that absorbs all radiation incident on it. The electromagnetic radiation
emitted by the black body is called blackbody radiation.
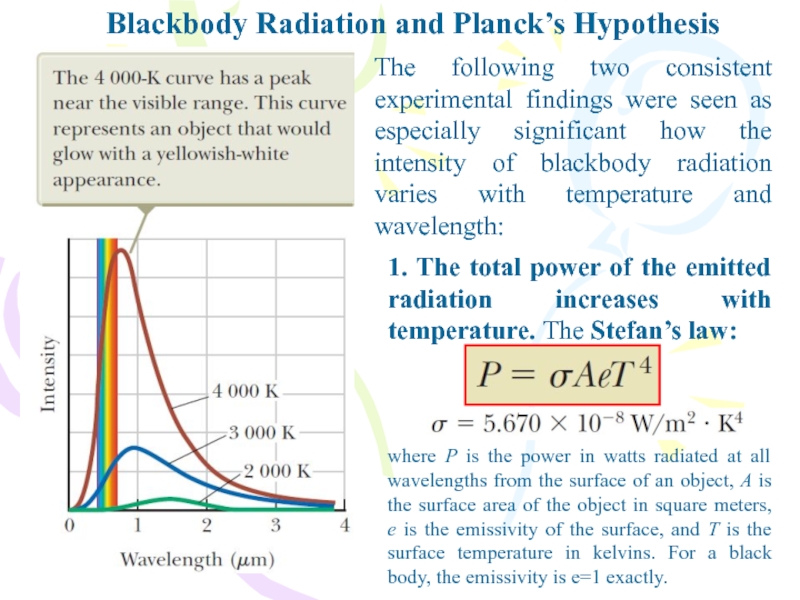
Слайд 5Blackbody Radiation and Planck’s Hypothesis
The following two consistent experimental findings
were seen as especially significant how the intensity of blackbody
radiation varies with temperature and wavelength:1. The total power of the emitted radiation increases with temperature. The Stefan’s law:
where P is the power in watts radiated at all wavelengths from the surface of an object, A is the surface area of the object in square meters, e is the emissivity of the surface, and T is the surface temperature in kelvins. For a black body, the emissivity is e=1 exactly.
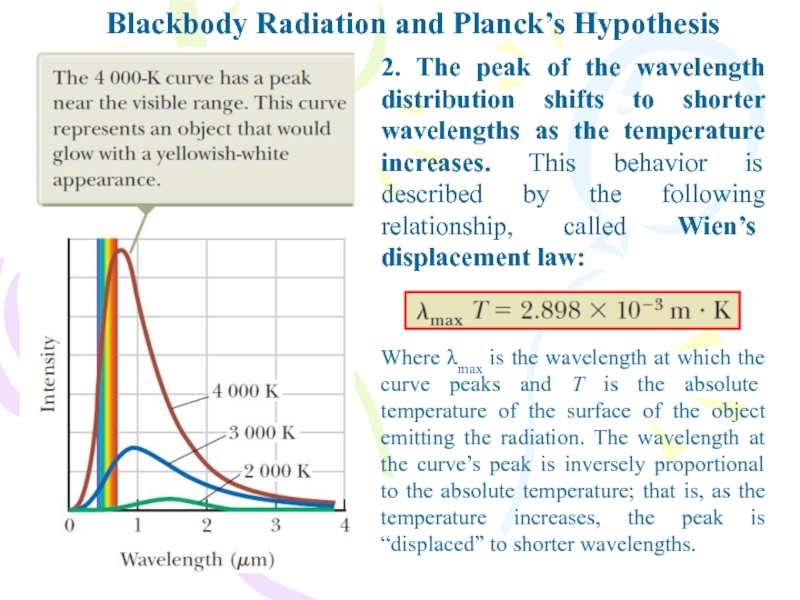
Слайд 6Blackbody Radiation and Planck’s Hypothesis
2. The peak of the wavelength
distribution shifts to shorter wavelengths as the temperature increases. This
behavior is described by the following relationship, called Wien’s displacement law:Where λmax is the wavelength at which the curve peaks and T is the absolute temperature of the surface of the object emitting the radiation. The wavelength at the curve’s peak is inversely proportional to the absolute temperature; that is, as the temperature increases, the peak is “displaced” to shorter wavelengths.
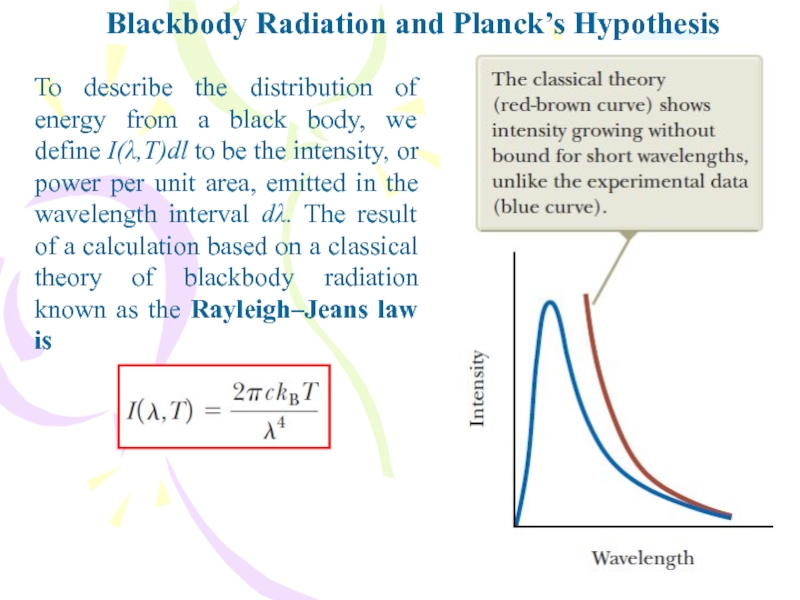
Слайд 7Blackbody Radiation and Planck’s Hypothesis
To describe the distribution of energy
from a black body, we define I(λ,T)dl to be the
intensity, or power per unit area, emitted in the wavelength interval dλ. The result of a calculation based on a classical theory of blackbody radiation known as the Rayleigh–Jeans law isСлайд 8Blackbody Radiation and Planck’s Hypothesis
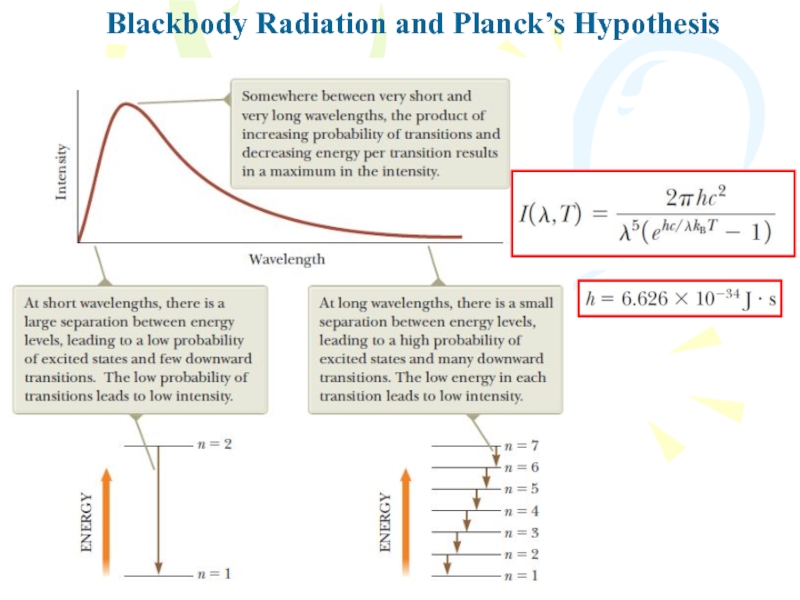
In 1900, Max Planck developed a
theory of blackbody radiation that leads to an equation for
I(λ,T) that is in complete agreement with experimental results at all wavelengths. Planck assumed the cavity radiation came from atomic oscillators in the cavity walls. Planck made two bold and controversial assumptions concerning the nature of the oscillators in the cavity walls:• The energy of an oscillator can have only certain discrete values En:
Because the energy of each oscillator can have only discrete values, we say the energy is quantized. Each discrete energy value corresponds to a different quantum state, represented by the quantum number n. When the oscillator is in the n=1 quantum state, its energy is hf ; when it is in the n=2 quantum state, its energy is 2hf; and so on.
Слайд 9Blackbody Radiation and Planck’s Hypothesis
• The oscillators emit or absorb
energy when making a transition from one quantum state to
another. The entire energy difference between the initial and final states in the transition is emitted or absorbed as a single quantum of radiation. If the transition is from one state to a lower adjacent state—say, from the n=3 state to the n=2 state the amount of energy emitted by the oscillator and carried by the quantum of radiation isСлайд 10Blackbody Radiation and Planck’s Hypothesis
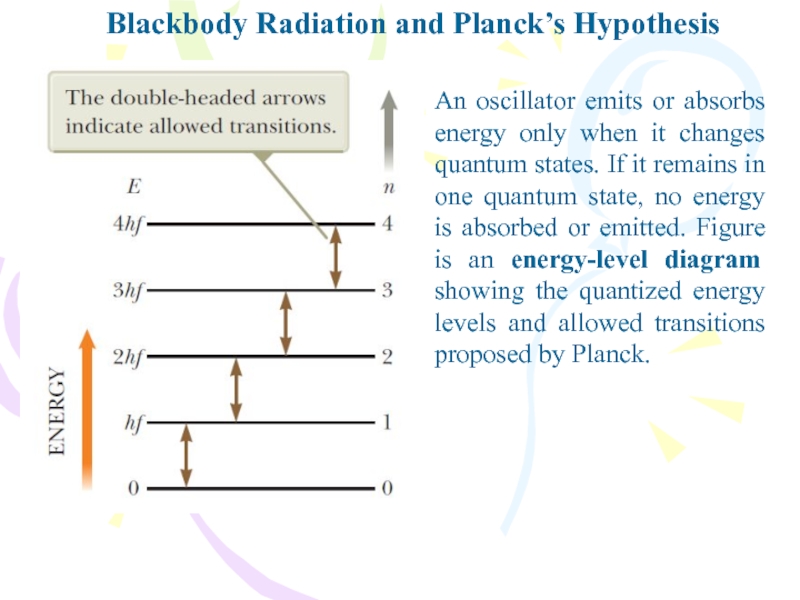
An oscillator emits or absorbs energy
only when it changes quantum states. If it remains in
one quantum state, no energy is absorbed or emitted. Figure is an energy-level diagram showing the quantized energy levels and allowed transitions proposed by Planck.Слайд 12The Photoelectric Effect
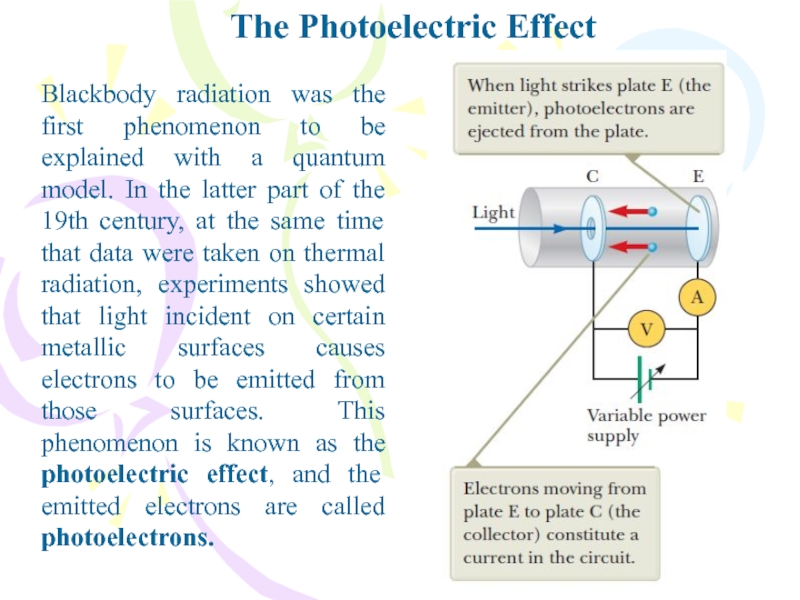
Blackbody radiation was the first phenomenon to be
explained with a quantum model. In the latter part of
the 19th century, at the same time that data were taken on thermal radiation, experiments showed that light incident on certain metallic surfaces causes electrons to be emitted from those surfaces. This phenomenon is known as the photoelectric effect, and the emitted electrons are called photoelectrons.Слайд 14The Photoelectric Effect
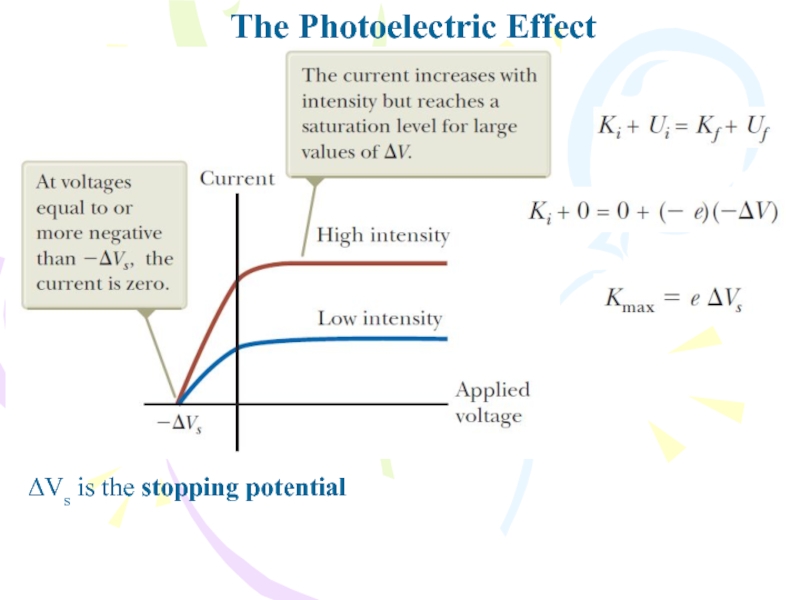
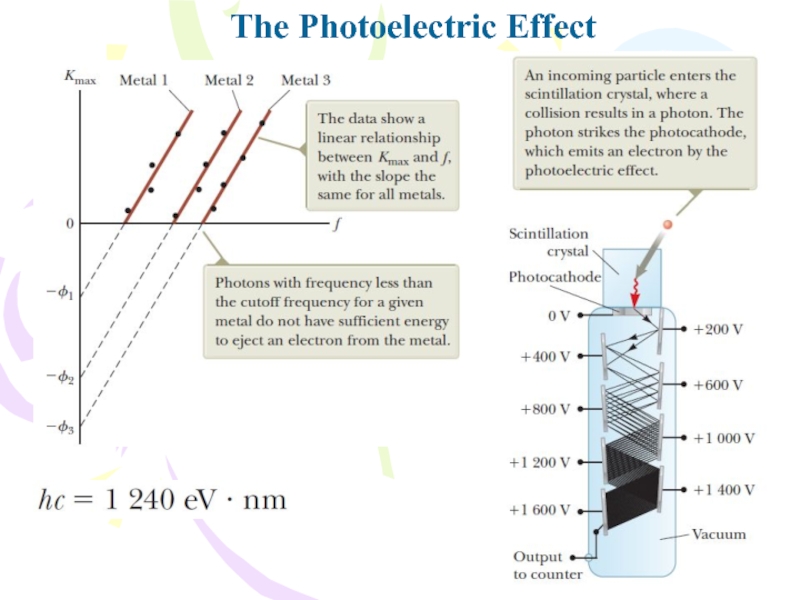
In Einstein’s model of the photoelectric effect, a
photon of the incident light gives all its energy hf
to a single electron in the metal. Therefore, the absorption of energy by the electrons is not a continuous absorption process as envisioned in the wave model; rather, it is a discontinuous process in which energy is delivered to the electrons in discrete bundles. The energy transfer is accomplished via a one photon–one electron event. Electrons ejected from the surface of the metal and not making collisions with other metal atoms before escaping possess the maximum kinetic energy Kmax. According to Einstein, the maximum kinetic energy for these liberated electrons iswhere ϕ is called the work function of the metal. The work function ϕ represents the minimum energy with which an electron is bound in the metal and is on the order of a few electron volts.
Слайд 15The Photoelectric Effect
Rearranging the equation:
cutoff wavelength λc
cutoff frequency fc,
Einstein assumed
light (or any other electromagnetic wave) of frequency f from
any source can be considered a stream of quanta. Today we call these quanta photons.Слайд 17The Compton Effect
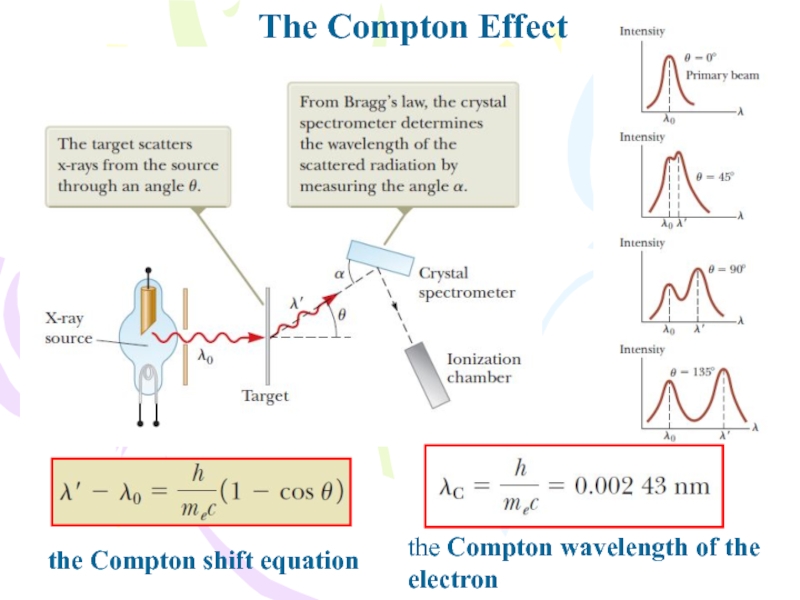
Because different electrons move at different speeds after
the interaction, depending on the amount of energy absorbed from
the electromagnetic waves, the scattered wave frequency at a given angle to the incoming radiation should show a distribution of Doppler-shifted values. Contrary to this prediction, Compton’s experiments showed that at a given angle only one frequency of radiation is observed. Compton and his coworkers explained these experiments by treating photons not as waves but rather as point-like particles having energy hf and momentum hf/c and by assuming the energy and momentum of the isolated system of the colliding photon–electron pair are conserved. Compton adopted a particle model for something that was well known as a wave, and today this scattering phenomenon is known as the Compton effect.Слайд 20The Nature of Electromagnetic Waves
Phenomena such as the photoelectric effect
and the Compton effect offer ironclad evidence that when light
(or other forms of electromagnetic radiation) and matter interact, the light behaves as if it were composed of particles having energy hf and momentum h/λ. How can light be considered a photon (in other words, a particle) when we know it is a wave? On the one hand, we describe light in terms of photons having energy and momentum. On the other hand, light and other electromagnetic waves exhibit interference and diffraction effects, which are consistent only with a wave interpretation.Слайд 21The Nature of Electromagnetic Waves
Some experiments can be explained either
better or solely with the photon model, whereas others are
explained either better or solely with the wave model. We must accept both models and admit that the true nature of light is not describable in terms of any single classical picture. The same light beam that can eject photoelectrons from a metal (meaning that the beam consists of photons) can also be diffracted by a grating (meaning that the beam is a wave). In other words, the particle model and the wave model of light complement each other.Слайд 22The Wave Properties of Particles
Every large-scale observation can be interpreted
by considering either a wave explanation or a particle explanation,
but in the world of photons and electrons, such distinctions are not as sharply drawn.Even more disconcerting is that, under certain conditions, the things we unambiguously call “particles” exhibit wave characteristics. In 1923 Louis de Broglie postulated that because photons have both wave and particle characteristics, perhaps all forms of matter have both properties. This highly revolutionary idea had no experimental confirmation at the time. According to de Broglie, electrons, just like light, have a dual particle–wave nature.
the de Broglie wavelength of that particle
Слайд 23The Wave Properties of Particles
Furthermore, in analogy with photons, de
Broglie postulated that particles obey the Einstein relation E=hf, where
E is the total energy of the particle. The frequency of a particle is thenThe principle of complementarity states that
the wave and particle models of either matter or radiation complement each other.
Neither model can be used exclusively to describe matter or radiation adequately. Because humans tend to generate mental images based on their experiences from the everyday world (baseballs, water waves, and so forth), we use both descriptions in a complementary manner to explain any given set of data from the quantum world.
Слайд 24The Wave Properties of Particles
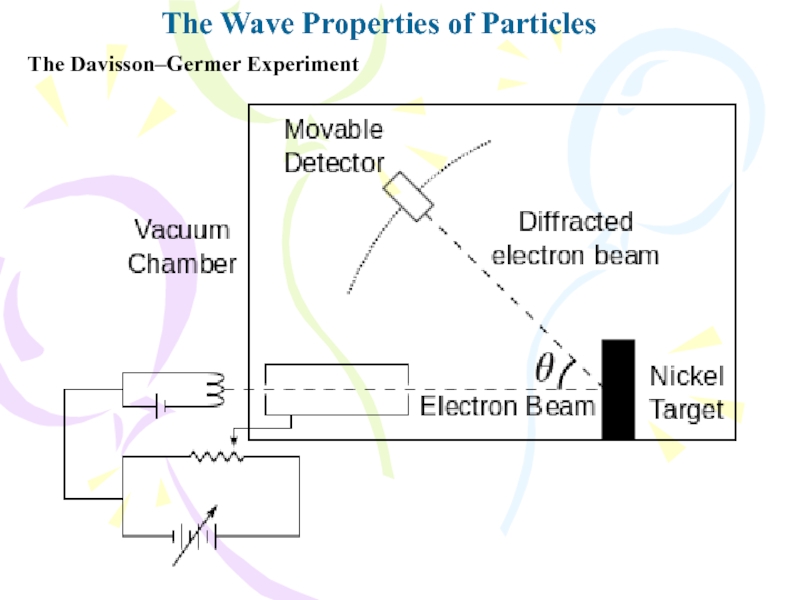
The Davisson–Germer Experiment
The experiment involved the
scattering of low-energy electrons (approximately 54 eV) from a nickel
target in a vacuum. During one experiment, the nickel surface was badly oxidized because of an accidental break in the vacuumsystem. After the target was heated in a flowing stream of hydrogen to remove the oxide coating, electrons scattered by it exhibited intensity maxima and minima at specific angles. The experimenters finally realized that the nickel had formed large crystalline regions upon heating and that the regularly spaced planes of atoms in these regions served as a diffraction grating for electrons.
Слайд 26The Wave Properties of Particles
The Davisson–Germer Experiment
Shortly thereafter, Davisson and
Germer performed more extensive diffraction measurements on electrons scattered from
single-crystal targets. Their results showed conclusively the wave nature of electrons and confirmed the de Broglie relationship p=h/l. In the same year, G. P. Thomson (1892–1975) of Scotland also observed electron diffraction patterns by passing electrons through very thin gold foils. Diffraction patterns have since been observed in the scattering of helium atoms, hydrogen atoms, and neutrons. Hence, the wave nature of particles has been established in various ways.Слайд 27The Wave Properties of Particles
The Electron Microscope
A practical device that
relies on the wave characteristics of electrons is the electron
microscope.Слайд 28A New Model: The Quantum Particle
Because in the past we
considered the particle and wave models to be distinct, the
discussions presented in previous sections may be quite disturbing. The notion that both light and material particles have both particle and wave properties does not fit with this distinction. Experimental evidence shows, however, that this conclusion is exactly what we must accept. The recognition of this dual nature leads to a new model, the quantum particle, which is a combination of the particle model and the wave model. In this new model, entities have both particle and wave characteristics, and we must choose one appropriate behavior—particle or wave—to understand a particular phenomenon.We shall explore this model in a way that might make you more comfortable with this idea. We shall do so by demonstrating that an entity that exhibits properties of a particle can be constructed from waves.
Слайд 29A New Model: The Quantum Particle
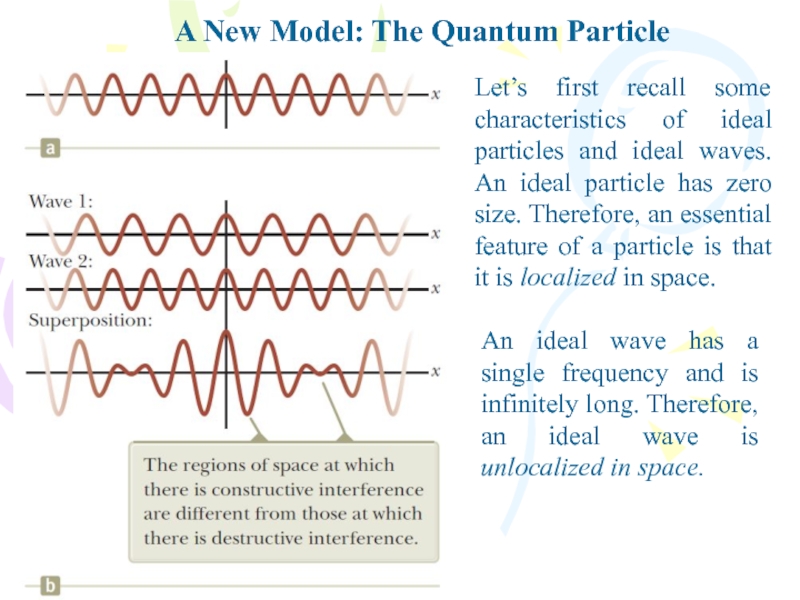
Let’s first recall some characteristics
of ideal particles and ideal waves. An ideal particle has
zero size. Therefore, an essential feature of a particle is that it is localized in space.An ideal wave has a single frequency and is infinitely long. Therefore, an ideal wave is unlocalized in space.
Слайд 30A New Model: The Quantum Particle
If a large number of
waves are combined, the result is a wave packet, which
represents a particle.We can identify the wave packet as a particle because it has the localized nature of a particle!
Слайд 31A New Model: The Quantum Particle
The second cosine factor represents
a wave with a wave number and frequency that are
equal to the averages of the values for the individual waves.Слайд 32A New Model: The Quantum Particle
For an individual wave, the
speed is given by
This speed is called the phase speed
because it is the rate of advance of a crest on a single wave, which is a point of fixed phase. This equation can be interpreted as follows: the phase speed of a wave is the ratio of the coefficient of the time variable t to the coefficient of the space variable x in the equation representing the wave, y=Acos(kx-vt).Слайд 33A New Model: The Quantum Particle
The group speed, or the
speed of the wave packet (the group of waves) we
have built.When a large number of waves are superposed to form a wave packet, this ratio becomes a derivative:
Слайд 34A New Model: The Quantum Particle
The group speed of the
wave packet is identical to the speed of the particle
that it is modeled to represent, giving us further confidence that the wave packet is a reasonable way to build a particle.Слайд 35The Double-Slit Experiment Revisited
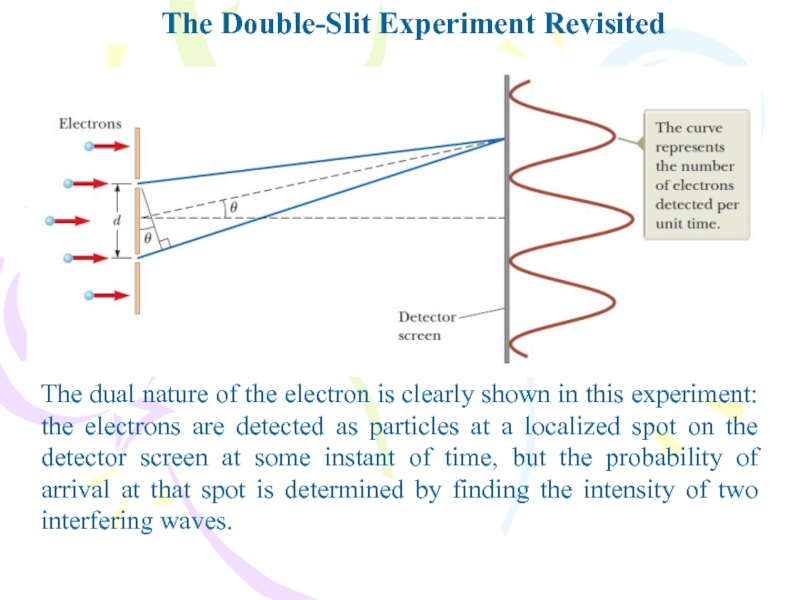
The dual nature of the electron is
clearly shown in this experiment: the electrons are detected as
particles at a localized spot on the detector screen at some instant of time, but the probability of arrival at that spot is determined by finding the intensity of two interfering waves.Слайд 37The Uncertainty Principle
Whenever one measures the position or velocity of
a particle at any instant, experimental uncertainties are built into
the measurements. According to classical mechanics, there is no fundamental barrier to an ultimate refinement of the apparatus or experimental procedures. In other words, it is possible, in principle, to make such measurements with arbitrarily small uncertainty. Quantum theory predicts, however, that it is fundamentally impossible to make simultaneous measurements of a particle’s position and momentum with infinite accuracy.Слайд 38The Uncertainty Principle
If a measurement of the position of a
particle is made with uncertainty Δx and a simultaneous measurement
of its x component of momentum is made with uncertainty Δpx, the product of the two uncertainties can never be smaller than ħ/2:In 1927, Werner Heisenberg (1901–1976) introduced this notion, which is now known as the Heisenberg uncertainty principle:
Слайд 39The Uncertainty Principle
The form of the uncertainty principle given in
this equation suggests that energy conservation can appear to be
violated by an amount ΔE as long as it is only for a short time interval Δt consistent with that equation.Imagine that the horizontal axis is time rather than spatial position x. We can then make the same arguments that were made about knowledge of wavelength and position in the time domain. The corresponding variables would be frequency and time. Because frequency is related to the energy of the particle by E=hf, the uncertainty principle in this form is