Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Абсолютные относительные и средние величины
Содержание
- 1. Абсолютные относительные и средние величины
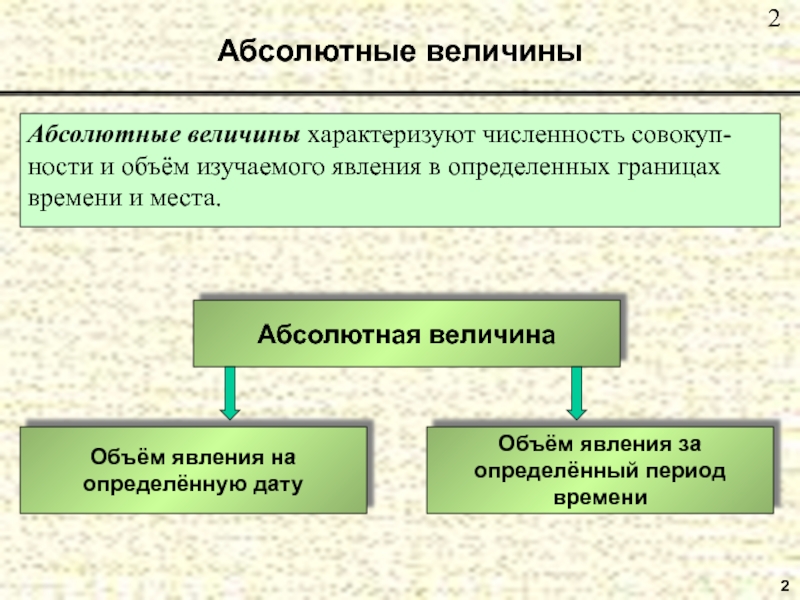
- 2. Абсолютные величиныАбсолютные величины характеризуют численность совокуп-ности и объём изучаемого явления в определенных границахвремени и места.Абсолютная величина2
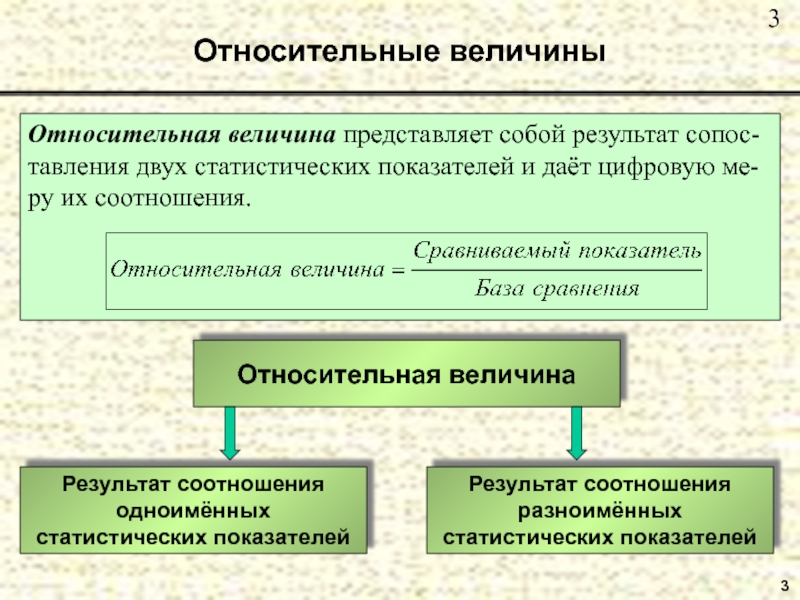
- 3. Относительные величиныОтносительная величина представляет собой результат сопос-тавления
- 4. Относительные величины одноимённых статистических показателей в экономике41.
- 5. Относительные величины одноимённых статистических показателей в экономике5Пример.
- 6. Относительные величины одноимённых статистических показателей в экономике6
- 7. Относительные величины одноимённых статистических показателей в экономике7
- 8. Относительные величины разноимённых статистических показателей в экономике8Эта группа статистических показателей носит название отно-сительных величин интенсивности.
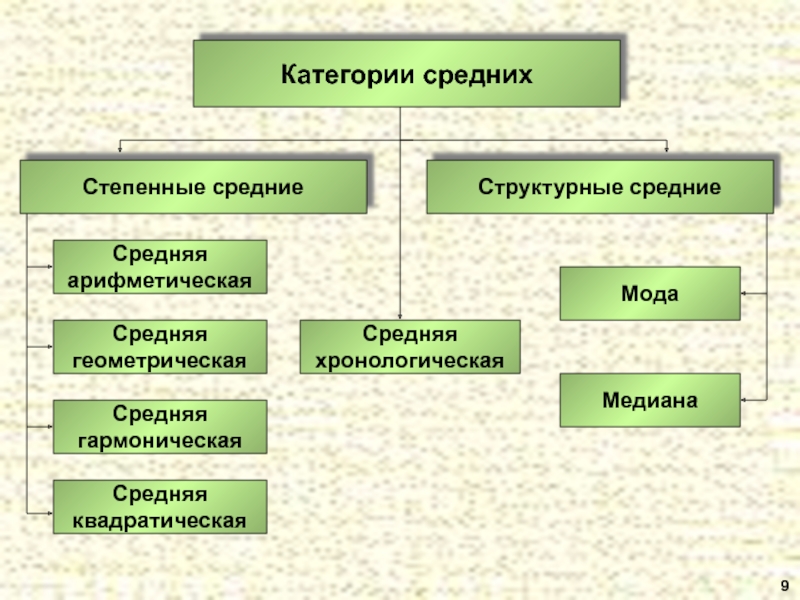
- 9. 9
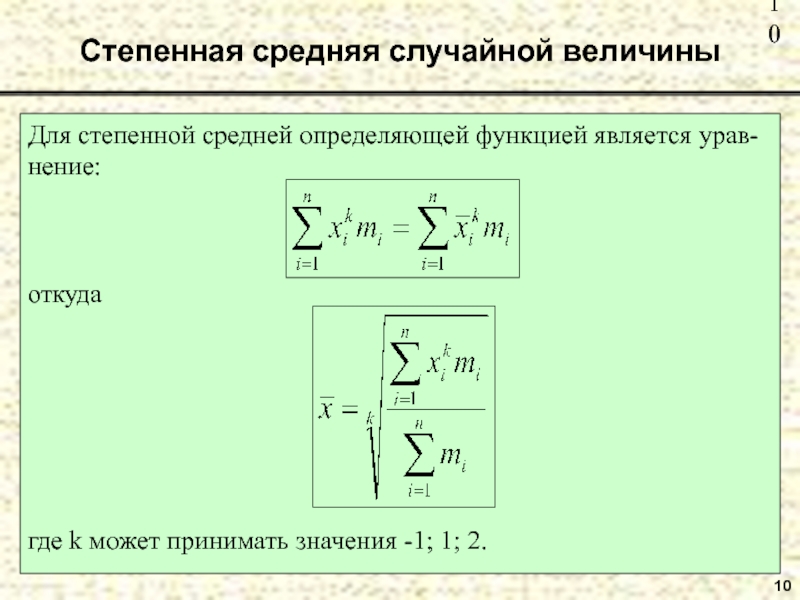
- 10. Степенная средняя случайной величины10
- 11. Среднее арифметическое значение случайной величины (k=1)Средним арифметичским
- 12. Среднее арифметическое значение случайной величины (k=1)12
- 13. Среднее значение суммы случайных величинСреднее значение суммы
- 14. Среднее значение произведения случайных величинСреднее значение произведения
- 15. Среднее гармоническое значение случайных величин (k= -1)Если
- 16. Среднее квадратическое значение случайных величин (k=2)Если случайная
- 17. Среднее геометрическое значение случайных величинЕсли случайная величина
- 18. Среднее геометрическое значение случайных величинПример. Перевозка грузов
- 19. Если случайные величины y1, y2,…, yn представляют
- 20. Пример №1. На 1 января 2001 года
- 21. Пример №2. Определить на сколько рублей и
- 22. Средняя хронологическая случайных величин22
- 23. В случае, если характер изменения уровней ряда
- 24. Пример. Средняя численность работников предприятий розничной торговли Российской Федерации характеризуется следующими данными:Средняя хронологическая случайных величин24
- 25. В случае, если промежутки времени между датами,
- 26. Пример №1. Товарные запасы ОАО «Золотой век»
- 27. Пример №2. Имеются следующие данные о стоимости
- 28. Модой называется значение признака, которое наиболее часто
- 29. Мода29Пример №2. Проведена малая выборка из партии
- 30. Мода302. Нахождение модальной величины в интервальном вариаци-онном
- 31. Мода31Пример. В таблице приведены данные о торговой площади магазинов:Необходимо рассчитать моду из интервального ряда.
- 32. Медиана32Медианой называется серединная варианта упорядоченного вариационного ряда,
- 33. Медиана332. Нахождение медианы интервального ряда. где: xo
- 34. Медиана34Пример. В таблице даны группы семей по
- 35. Медиана35Пример. Филиалы торговой фирмы «Элегант» расположены на
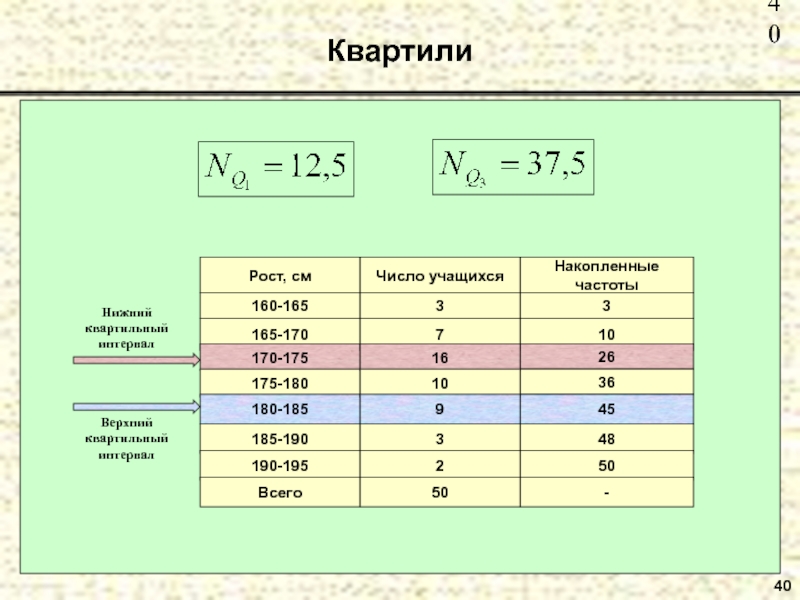
- 36. Квартили36Более общая постановка вариант, занимающих определённое место
- 37. Квартили37 Нижний квартиль: Верхний квартиль:где: xo
- 38. Квартили38Пример. Дан интервальный ряд распределения 50 учащихся по росту:Определить нижний и верхний квартиль.
- 39. Квартили39 Место нижнего квартиля: Место медианы ранжированного интервального ряда: Место верхнего квартиля:
- 40. Квартили40
- 41. Квартили41 Нижний квартиль: Верхний квартиль:
- 42. Скачать презентанцию
Абсолютные величиныАбсолютные величины характеризуют численность совокуп-ности и объём изучаемого явления в определенных границахвремени и места.Абсолютная величина2
Слайды и текст этой презентации
Слайд 1Автор: Равичев Л.В.
РХТУ им. Д.И.Менделеева
Кафедра управления технологическими инновациями
Москва - 2013
СТАТИСТИКА.
Лекция 1. Абсолютные, относительные и средние величины. Мода и медиана.
статистика.
Слайд 2Абсолютные величины
Абсолютные величины характеризуют численность совокуп-
ности и объём изучаемого явления
в определенных границах
времени и места.
Абсолютная величина
2
Слайд 3Относительные величины
Относительная величина представляет собой результат сопос-тавления двух статистических показателей
и даёт цифровую ме-ру их соотношения.
Относительная величина
3
Слайд 4
Относительные величины одноимённых статистических показателей в экономике
4
1. Относительные величины динамики
характеризует измене-ние явления во времени. Они показывают во сколько раз
изме-нится объём явления за определённый период времени, т.е. тем-пы роста.
Слайд 5
Относительные величины одноимённых статистических показателей в экономике
5
Пример. Имеются следующие данные
о стоимости основного капитала по фирме:
Определить показатели динамики стоимости основного
капитала фирмы.Решение:
на 1 января 1999 г. – y1 = 22 150 + 7 380 + 13 970 = 43 500
на 1 января 2000 г. – y2 = 24 855 + 9 100 + 16 700 = 50 655
на 1 января 2001 г. – y3 = 26 970 + 12 550 + 20 800 = 60 320
1) Темпы роста с переменной базой:
2) Темпы роста с постоянной базой (за постоянную базу принимаем данные на 01.01.99г.) :
Слайд 8
Относительные величины разноимённых статистических показателей в экономике
8
Эта группа статистических показателей
носит название отно-сительных величин интенсивности.
Слайд 11Среднее арифметическое значение случайной величины (k=1)
Средним арифметичским значением дискретной случайной
ве-
личины называют сумму произведений всех ее возможных зна-
чений на их
вероятности. Если x имеет конечное число значенийxi, которые встречаются fi раз то среднее значение x вычисляют
по формуле:
В самом простом случае, когда значения xi встречаются только
по одному разу, формула упрощается и принимает вид:
11
Слайд 13Среднее значение суммы случайных величин
Среднее значение суммы случайных величин равно
сумме
средних значений случайных величин. Так, для двух наборов
случайных величин
Х1, Х2,…, Хk и Y1, Y2,.…, Yn, с соответству-ющими вероятностями появления p1, p2,…, pk и q1, q2,.…, qn, рас-
четная формула имеет вид:
В случае большего количества наборов случайных величин фор-
мула имеет аналогичный вид:
13
Слайд 14Среднее значение произведения случайных величин
Среднее значение произведения взаимно независимых случай-
ных
величин равно произведению средних значений случайных
величин. Так, для двух
наборов независимых случайных величинХ1, Х2,…, Хk и Y1, Y2,.…, Yn, с соответствующими вероятностя-
ми появления p1, p2,…, pk и q1, q2,.…, qn, расчетная формула име-
ет вид:
14
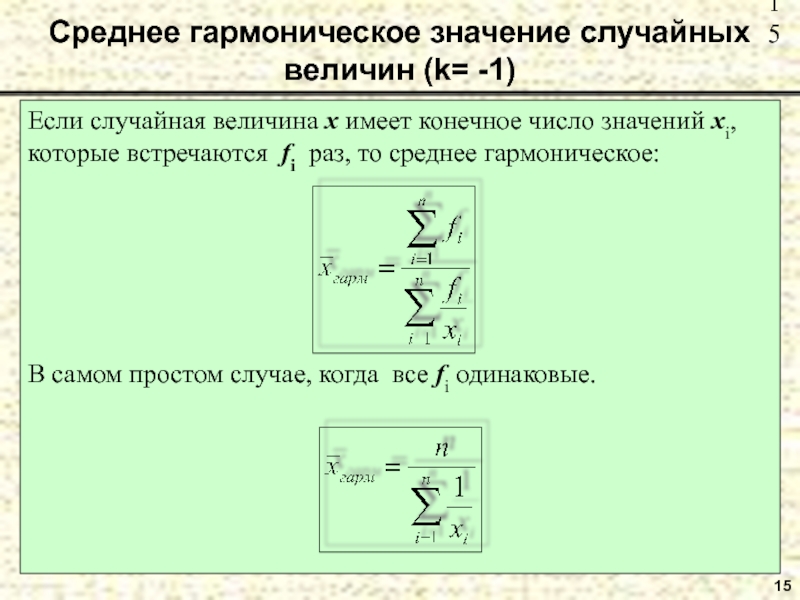
Слайд 15Среднее гармоническое значение случайных величин (k= -1)
Если случайная величина x
имеет конечное число значений xi,
которые встречаются fi раз, то
среднее гармоническое:В самом простом случае, когда все fi одинаковые.
15
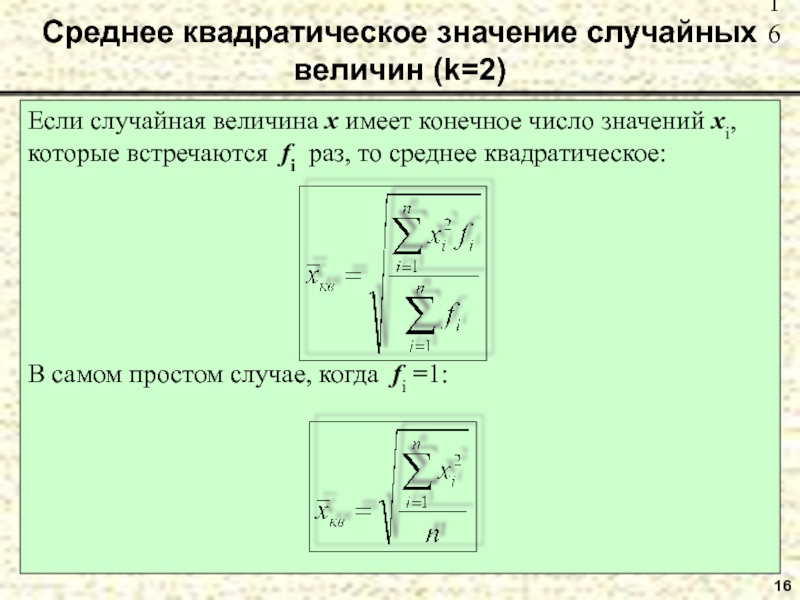
Слайд 16Среднее квадратическое значение случайных величин (k=2)
Если случайная величина x имеет
конечное число значений xi,
которые встречаются fi раз, то среднее
квадратическое:В самом простом случае, когда fi =1:
16
Слайд 17Среднее геометрическое значение случайных величин
Если случайная величина x имеет конечное
число значений xi,
которые встречаются fi раз, то среднее геометрическое
значениеx вычисляют по формуле:
В самом простом случае, когда значения xi встречаются только
по одному разу, формула упрощается и принимает вид:
17
Слайд 18Среднее геометрическое значение случайных величин
Пример. Перевозка грузов по автотранспортному предприятию
такова:
Определить среднемесячный темп роста объёма грузовых пере-
возок.
Решение: Коэффициенты роста объёма
грузовых перевозок:Среднемесячный коэффициент роста определяется по формуле
средней геометрической:
или 106,6% (средний темп роста).
18
Слайд 19Если случайные величины y1, y2,…, yn представляют собой мо-
ментальный динамический
ряд, то средний уровень такого ряда
оценивается по формуле средней хронологической
взвешенной:
Где - средний уровень ряда; yi – уровни динамического
ряда; - время, в течение которого данный уровень ряда оста-
вался неизменным.
Средняя хронологическая случайных величин
19
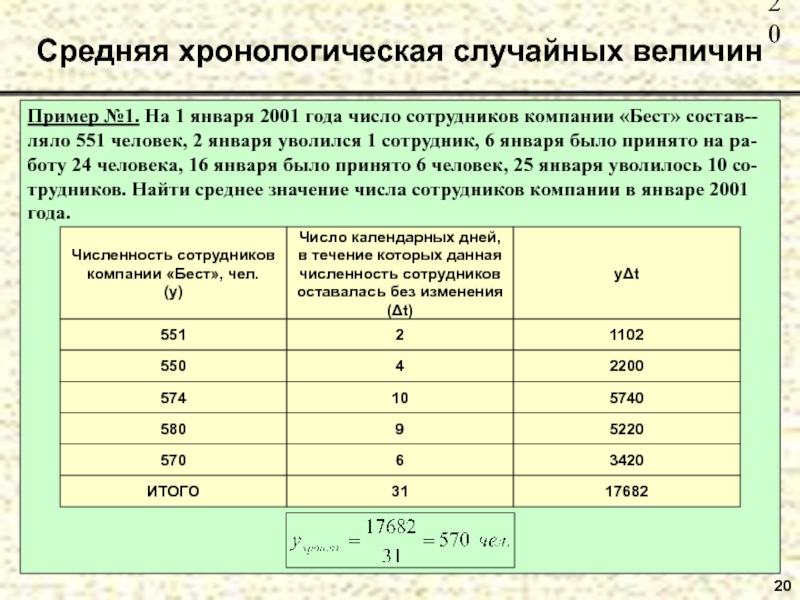
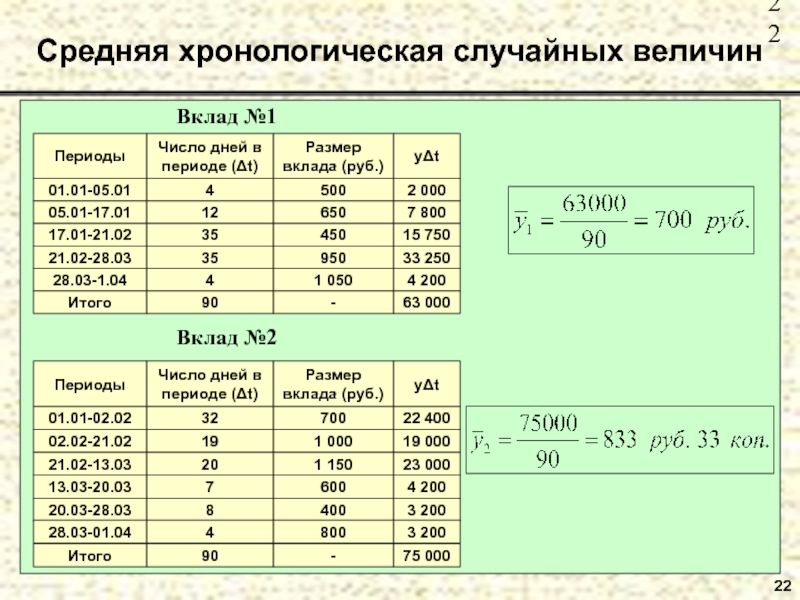
Слайд 20Пример №1. На 1 января 2001 года число сотрудников компании
«Бест» состав--ляло 551 человек, 2 января уволился 1 сотрудник, 6
января было принято на ра-боту 24 человека, 16 января было принято 6 человек, 25 января уволилось 10 со-трудников. Найти среднее значение числа сотрудников компании в январе 2001 года.Средняя хронологическая случайных величин
20
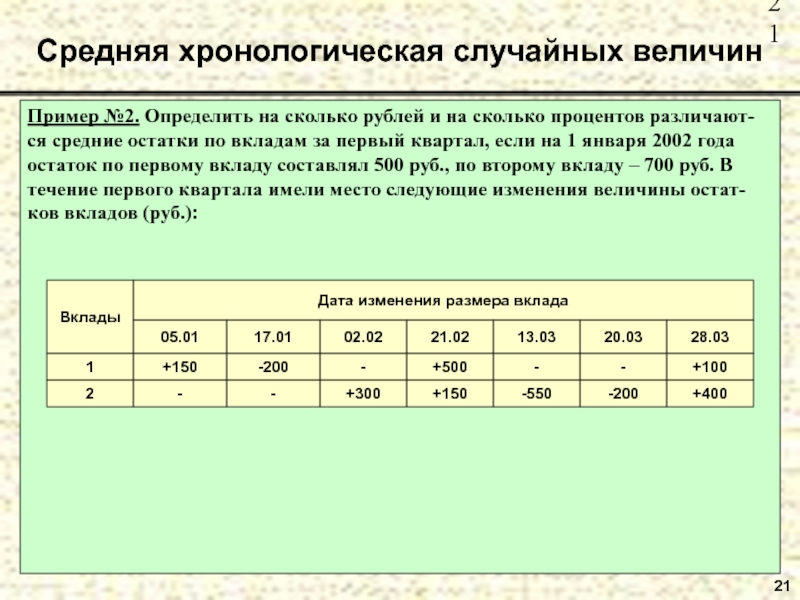
Слайд 21Пример №2. Определить на сколько рублей и на сколько процентов
различают-ся средние остатки по вкладам за первый квартал, если на
1 января 2002 года остаток по первому вкладу составлял 500 руб., по второму вкладу – 700 руб. В течение первого квартала имели место следующие изменения величины остат-ков вкладов (руб.):Средняя хронологическая случайных величин
21
Слайд 23В случае, если характер изменения уровней ряда в рассматрива-емые периоды
неизвестен, и уровни ряда отстоят друг от друга на неравные
промежутки времени, то средняя хронологическая взвешенная вычисляется по формуле:Средняя хронологическая случайных величин
23
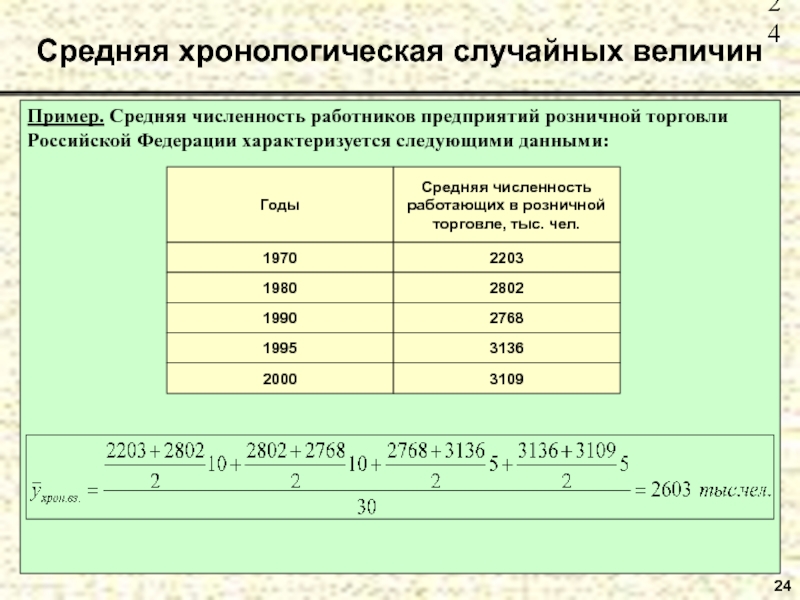
Слайд 24Пример. Средняя численность работников предприятий розничной торговли Российской Федерации характеризуется
следующими данными:
Средняя хронологическая случайных величин
24
Слайд 25В случае, если промежутки времени между датами, на которые имеются
данные одинаковы, и при равномерном изменении раз-мера показателя между датами
средняя хронологическая ряда вычисляется по формуле:где y1 и yn – начальный и конечный уровни ряда, n – число дат.
Средняя хронологическая случайных величин
25
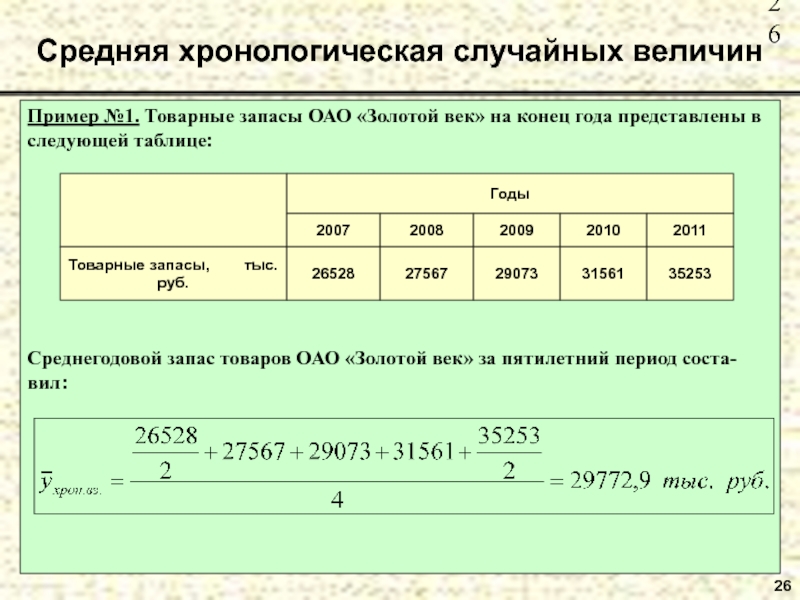
Слайд 26Пример №1. Товарные запасы ОАО «Золотой век» на конец года
представлены в следующей таблице:
Среднегодовой запас товаров ОАО «Золотой век» за
пятилетний период соста-вил:Средняя хронологическая случайных величин
26
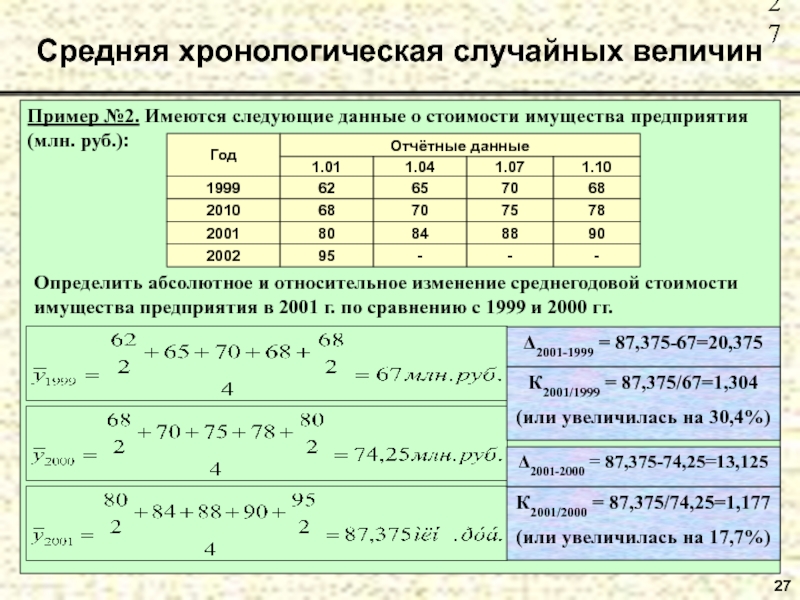
Слайд 27Пример №2. Имеются следующие данные о стоимости имущества предприятия (млн.
руб.):
Средняя хронологическая случайных величин
27
Определить абсолютное и относительное изменение среднегодовой стоимости
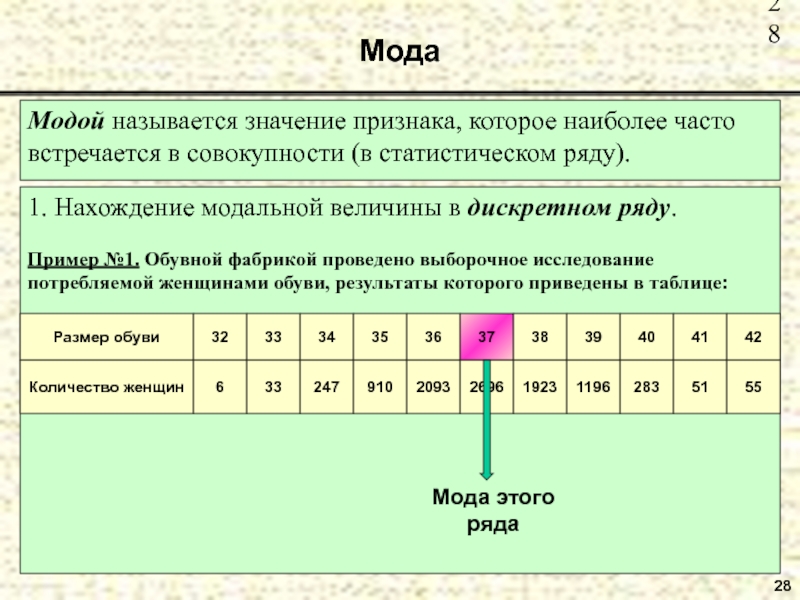
имущества предприятия в 2001 г. по сравнению с 1999 и 2000 гг.
Слайд 28Модой называется значение признака, которое наиболее часто встречается в совокупности
(в статистическом ряду).
Мода
28
1. Нахождение модальной величины в дискретном ряду.
Пример №1.
Обувной фабрикой проведено выборочное исследование потребляемой женщинами обуви, результаты которого приведены в таблице:Мода этого ряда
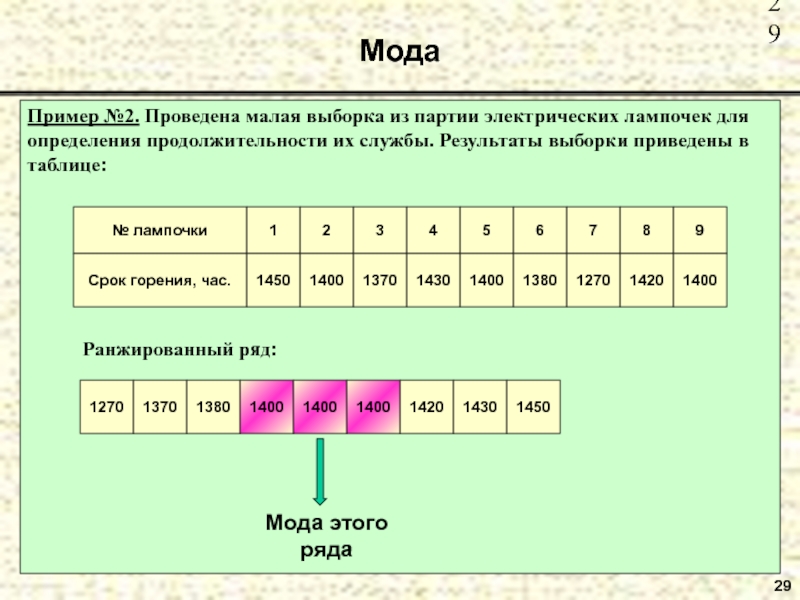
Слайд 29Мода
29
Пример №2. Проведена малая выборка из партии электрических лампочек для
определения продолжительности их службы. Результаты выборки приведены в таблице:
Ранжированный ряд:
Слайд 30Мода
30
2. Нахождение модальной величины в интервальном вариаци-онном ряду.
где: хmo- нижняя
граница модального интервала; i – разность между верхней и нижней
границей модального интервала; f1 – частота интервала, предшествующая модальному; f2 – частота модального интервала; f3 – частота интервала, следующего за модальным.
Слайд 31Мода
31
Пример. В таблице приведены данные о торговой площади магазинов:
Необходимо рассчитать
моду из интервального ряда.
Слайд 32Медиана
32
Медианой называется серединная варианта упорядоченного вариационного ряда, расположенного в возрастающем
или убывающем порядке (ранжированный вариационный ряд).
Нахождение медианы в дискретном
ранжированном вариа ционном ряду.Пример.
а) дан нечетный ранжированный вариационный ряд роста студенток:
б) дан четный ранжированный вариационный ряд роста студенток:
Ме=161; место медианы Nme=(n+1)/2=4.
Слайд 33Медиана
33
2. Нахождение медианы интервального ряда.
где: xo – нижняя граница
медианного интервала; i – величина медианного интервала; fi – частоты
интервального ряда; Sm-1 – сумма накопленных частот в интервалах предшествующих медианному; fm – частота медианного интервала.
Слайд 34Медиана
34
Пример. В таблице даны группы семей по среднемесячному доходу на
1 чело-века. Требуется для приведенного интервального ряда определить серединное значение,
т.е. медиану.Группы семей по среднемесячному доходу на 1 человека, руб.
До 900
Число семей
10
От 900 до 1200
20
От 1200 до 1500
40
От 1500 до 1800
10
Свыше 1800
20
ИТОГО
100
Следовательно, 50% семей имеют доход на одного человека <1350 руб.
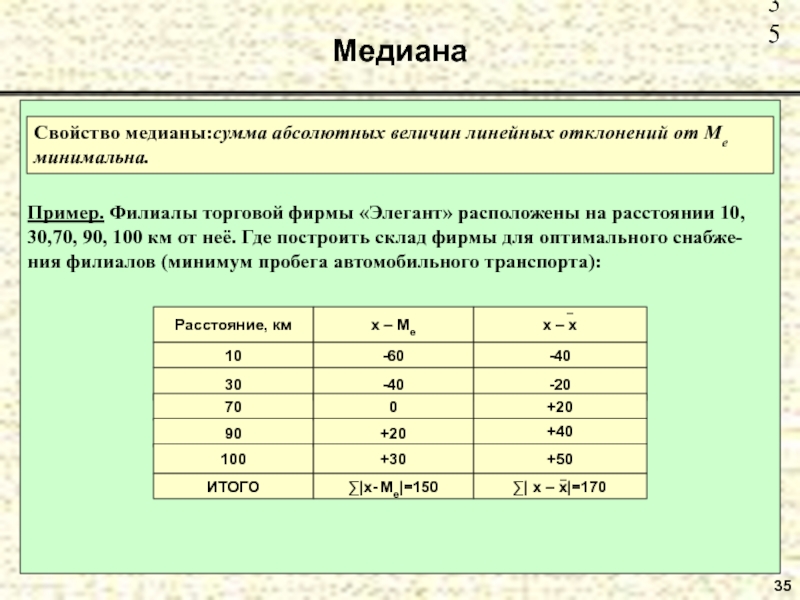
Слайд 35Медиана
35
Пример. Филиалы торговой фирмы «Элегант» расположены на расстоянии 10, 30,70,
90, 100 км от неё. Где построить склад фирмы для
оптимального снабже-ния филиалов (минимум пробега автомобильного транспорта):Свойство медианы:сумма абсолютных величин линейных отклонений от Ме минимальна.
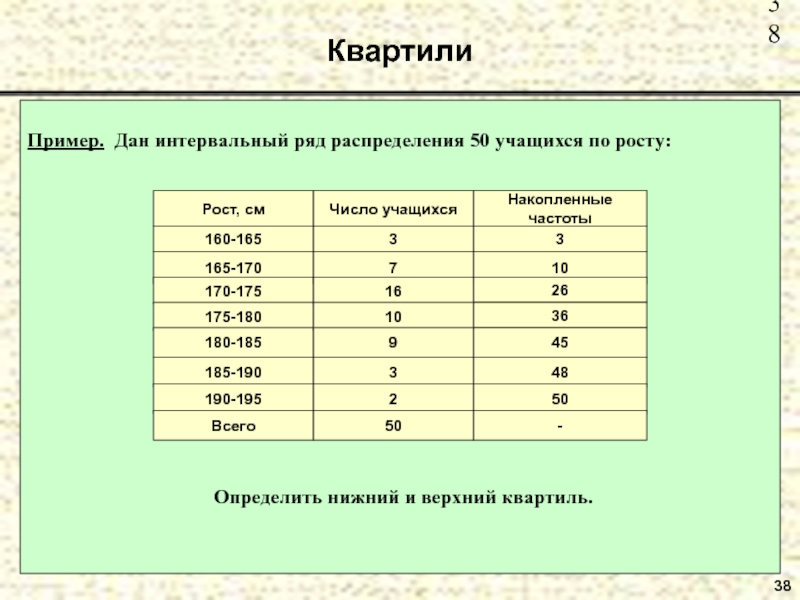
Слайд 36Квартили
36
Более общая постановка вариант, занимающих определённое место в ранжированном ряду,
называется порядковой статис-тикой.
Квартиль – значения признака, которые делят ранжированный
ряд на четыре равные по численности части. Таких величин будет три: первая квартиль (Q1), вторая квартиль (Q2), третья квартиль (Q3). Вторая квартиль является медианой.Место квартили:
Слайд 37Квартили
37
Нижний квартиль:
Верхний квартиль:
где: xo – нижняя
граница квартильных интервалов; i – величи-на интервала; fi – частоты
интервального ряда; SQ1 – сумма накопленных частот в интервалах предшествующих нижнему квартилю; SQ3 – сумма накопленных частот в интервалах предшествующих верхнему квартилю; fQ1, fQ3 – частота квартильного интервала.
Слайд 38Квартили
38
Пример. Дан интервальный ряд распределения 50 учащихся по росту:
Определить нижний
и верхний квартиль.
Слайд 39Квартили
39
Место нижнего квартиля:
Место медианы ранжированного интервального
ряда:
Место верхнего квартиля:
