Слайд 1АЛГОРИТМЫ
ГЕНЕРАЦИИ и
ТЕСТИРОВАНИЯ
СЛУЧАЙНЫХ
и
ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Слайд 2ОСНОВНЫЕ ТЕМЫ ЛЕКЦИИ
ОТЛИЧИЯ СЛУЧАЙНЫХ и ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
ВЫБОР ФИЗИЧЕСКИХ ДАТЧИКОВ ШУМА
БАЗОВАЯ МОДЕЛЬ ГЕНЕРАТОРА СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
ВЫРАВНИВАНИЕ ВЕРОЯТНОСТЕЙ ГЕНЕРИРУ-ЕМЫХ СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
МЕТОДЫ ПОВЫШЕНИЯ БЫСТРОДЕЙСТВИЯ ГЕНЕРАТОРОВ СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬ-НОСТЕЙ
МЕТОДЫ ТЕСТИРОВАНИЯ СЛУЧАЙНЫХ И ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ НА ОСНОВЕ МЕТОДИКИ FIPS 140-1.
Слайд 3 РЕАЛИЗАЦИЯ ПСЕВДОСЛУЧАЙНЫХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
С помощью цифровых логических схем можно
необычайно просто генерировать последовательности бит с хорошими стохастическими свойствами, т.е.
последовательности, которые будут обладать такими же вероятностными и корреляционными свойст-вами, какими обладает идеальная машина для подбрасывания монеты.
Поскольку эти последовательности генерируются стандартными элементами детерминированной логи-ки, получающиеся двоичные последовательности на самом деле являются предсказуемыми и повторяемы-ми (детерминированными), хотя любой фрагмент такой последовательности во всех отношениях выглядит, как случайное чередование «0» и «1».
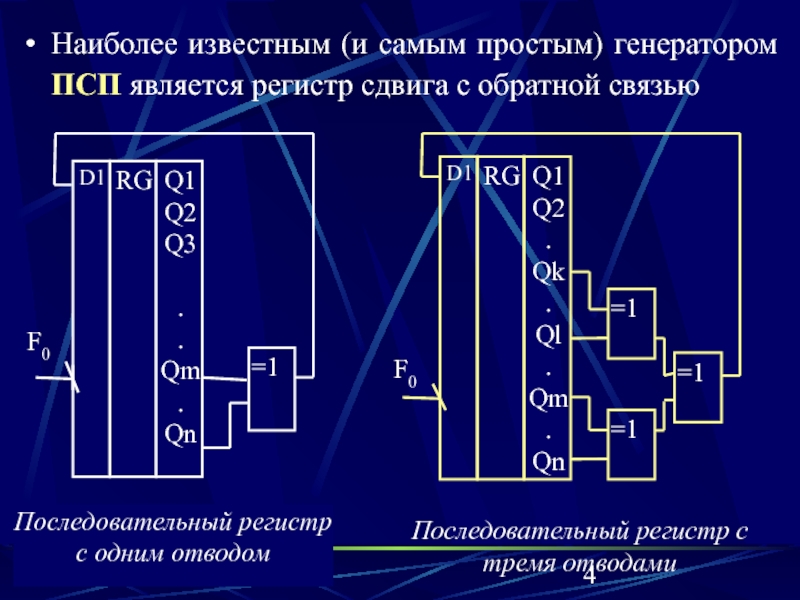
Слайд 4Наиболее известным (и самым простым) генератором ПСП является регистр сдвига
с обратной связью
Слайд 5 Последовательный регистр RG длиной «n» осуществляет сдвиг хранимого кода
после каждого тактового импульса с частотой Fo. Входной сигнал первого
триггера регистра – D1 формируется с помощью вентиля ИСКЛЮЧАЮЩЕЕ ИЛИ (сумма-тора по модулю 2), на входы которого поступают сигналы от m-того и последнего (n-того) разрядов регистра.
Такая схема проходит через множество состояний, которые после К тактов начинают повторяться, т.е. последовательность состояний является циклической с периодом К.
Слайд 6 Максимальное число возможных состояний n-разрядного регистра равно К=2n,
т.е. числу n-битовых двоичных комбинаций. Однако состояние «все нули» для
этой схемы является тупиковым, поскольку на выходе схемы ИСКЛЮЧАЮЩЕЕ ИЛИ постоянно появляются нули, которые поступают на вход схемы и зацикливаются.
Если для формирования входного сигнала использовать элемент «ИСКЛЮЧАЮЩЕЕ ИЛИ» с инверсией, то «тупиковой» будет комбинация – «все единицы».
Таким образом, последовательность максималь-ной длины, которую может сформировать данная схема, содержит 2n-1 бит.
Слайд 7При использовании 33-х разрядного регистра, работающего на частоте 1 МГц,
время цикла будет около 2-х часов. Время цикла 100 разрядного
регистра, работающего на частоте 10 МГц, будет в миллион раз больше, чем возраст Вселенной.
Генераторы ПСП на сдвигающих регистрах можно использовать для шифрования сообщений и данных, поскольку идентичный генератор ПСП на приемном конце дает ключ к шифру.
ПСП широко используются в кодах, обнаруживаю-щих и исправляющих ошибки, так как они позволяют видоизменить блоки данных таким образом, что правильные кодовые сообщения будут находиться друг от друга на максимально возмож-ном «расстоянии Хэмминга» (измеряется числом позиций с разными данными).
Слайд 8 СВОЙСТВА ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕ-ДОВАТЕЛЬНОСТЕЙ МАКСИМАЛЬНОЙ ДЛИНЫ
В полном цикле число
«1» на единицу больше, чем число «0». Добавочная «1» появляется
за счет исключения состояния «все нули». При большом количестве разрядов регистра вероятности «0» и «1» практически равны (17-ти разрядный регистр будет вырабатывать 65536 «1» и 65535 «0» за один цикл);
В одном цикле половина серий из последовательных «1» имеет длину 1, одна четвертая серий – длину 2, одна восьмая – длину 3 и т.д. Таким же свойством обладают и серии из «0» с учетом пропущенного «0». Это говорит о том, что вероятности «0» и «1» не зависят от исхода предыдущего опыта, т.е. вероятность появления «0» или «1» в следу-ющем бите не зависит от значения предыдущего бита;
Слайд 9Если последовательность полного цикла сравнить с этой же последовательностью, но
циклически сдвинутой на любое число битов (не равное нулю или
длине К), то число несовпадений будет на единицу больше, чем число совпадений. Научно выражаясь, автокорреляционная функция этой последовательности представляет собой дельта-функцию Кронекера при нулевой задержке и равна величине 1/К при любой другой задержке.
Слайд 10ОСНОВНЫЕ ОТЛИЧИЯ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ ОТ СЛУЧАЙНЫХ
Псевдослучайные числа
являются детерминиро-ванными, то есть предсказуемыми. Зная алгоритм формирования и начальное
значение, можно предсказать все последующие числа наперед.
В новом эксперименте всегда можно повторить предыдущий эксперимент.
Псевдослучайные последовательности являются периодическими, через известные промежутки времени они будут точно повторяться.
Слайд 11Предельные характеристики стойкости криптографических систем достигаются в случае, если для
формирования ключей, параметров и синхромаркеров используется генератор случайных последовательностей на
основе ФИЗИЧЕСКИХ ДАТЧИКОВ ШУМА с наилучшими параметрами:
равновероятности,
независимости и
некоррелированности на сколь угодно длинном интервале.
Слайд 12 Простейшие физические датчики, реализованные на основе случайных механических перемещений:
подбрасывание монеты,
бросание «игральных костей»,
наблюдения броуновского движения и др.
обладают недостаточным быстродействием и требуют для своей реализации оптические устройства ввода результатов опытов в ЭВМ.
Слайд 13Основные датчики шума
Критерии выбора
∙полоса частот случайного сигнала;
∙выходное напряжение (ам-плитуда шума);
∙
потребляемая мощность;
∙ напряжение питания;
∙массогабаритные парамет-ры;
∙ надежность работы при из-менении условий
эксплу-атации;
∙экономические показатели (стоимость).
Резисторы
P-n-переходы
Диоды с Зенеров-ским пробоем
Электр. лампы
Газоразрядные лампы
ФЭУ
Счетчики радиоактивности
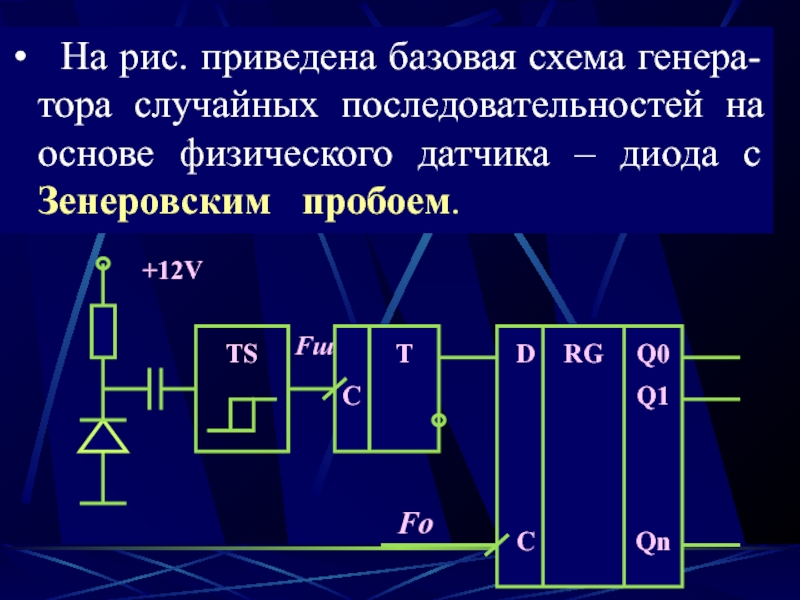
Слайд 14 На рис. приведена базовая схема генера-тора случайных последовательностей на
основе физического датчика – диода с Зенеровским пробоем.
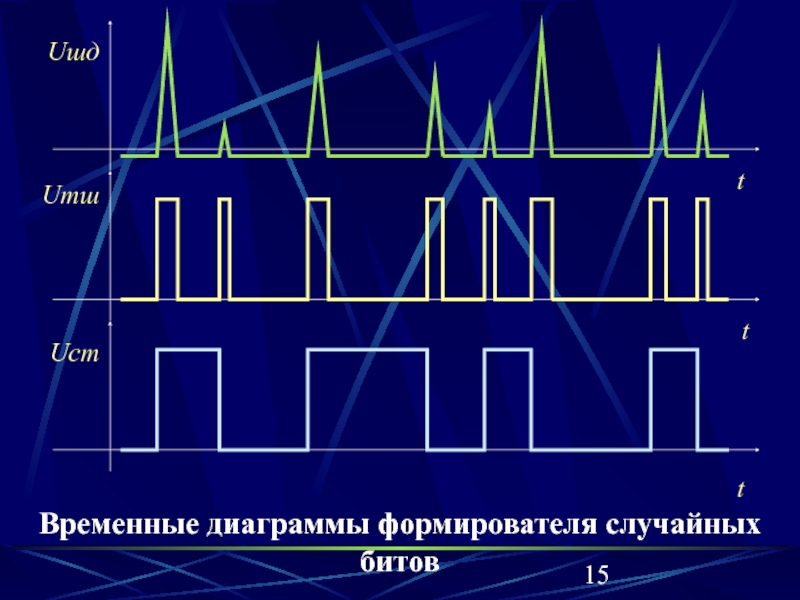
Слайд 15Временные диаграммы формирователя случайных битов
Uшд
Uтш
Uст
t
t
t
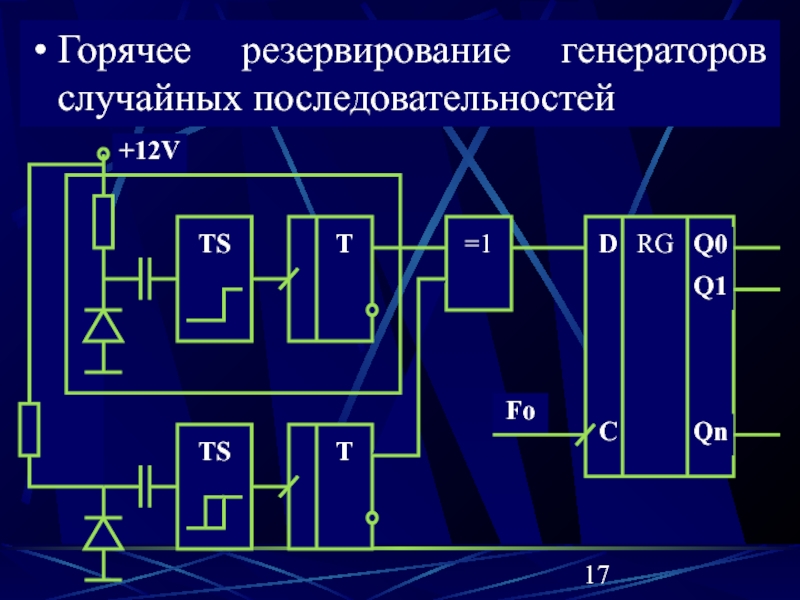
Слайд 16Повышение эксплуатационной надежности канала формирования случайных битов достигается горячим резервированием,
то есть параллельной работой нескольких каналов.
Выходные равновероятные случайные логи-ческие
сигналы всех каналов объединяются схемой «ИСКЛЮЧАЮЩЕЕ ИЛИ» (схемой суммирования по модулю 2) и считываются в сдвигающий регистр с частотой Fo
Слайд 17Горячее резервирование генераторов случайных последовательностей
Слайд 19ВЫРАВНИВАНИЕ ВЕРОЯТНОСТЕЙ ГЕНЕРИРУЕМЫХ СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Для выравнивания вероятностей из двух последовательных
случайных битов на выходах дополнительного регистра формируется их логическая функция
«ИСКЛЮЧАЮЩЕЕ ИЛИ».
Вероятность единичного формируемого бита на входе регистра RG1 обозначим Р(1), а вероятность нулевого – Р(0) = Р(1) + Δ.
Слайд 20Схема выравнивания вероятностей «Дельта-квадрат»
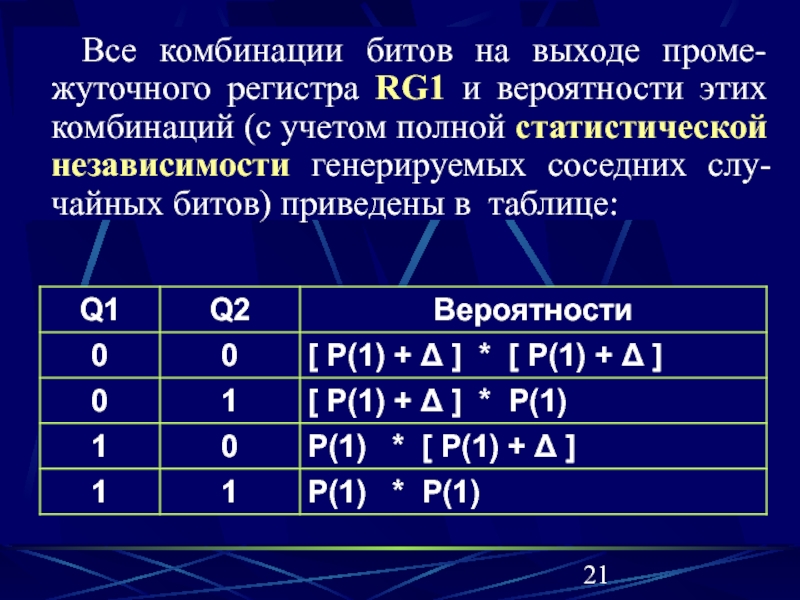
Слайд 21 Все комбинации битов на выходе проме-жуточного регистра RG1
и вероятности этих комбинаций (с учетом полной статистической независимости генерируемых
соседних слу-чайных битов) приведены в таблице:
Слайд 22На выходе схемы «ИСКЛЮЧАЮШЕЕ ИЛИ» формируется логический нуль при комби-нациях,
соответствующих первой и последней строкам таблицы:
P(0)' = [ Р(1) +
Δ ] * [ Р(1) + Δ ] + P(1) * P(1).
Логической единице на выходе схемы «ИСКЛЮЧАЮЩЕЕ ИЛИ» будут соответ-ствовать две средние строки в таблице:
P(1)' = [ P(1) + Δ ] * P(1) + P(1) * [ P(1) + Δ ].
Разность вероятностей на выходе схемы «ИСКЛЮЧАЮЩЕЕ ИЛИ» Δ' равна:
Δ' = P(0)' - P(1)' = Δ2.
Слайд 23Схема полного выравнивания вероятностей
Слайд 24МЕТОДЫ ПОВЫШЕНИЯ БЫСТРОДЕЙСТВИЯ ГЕНЕРАТОРОВ СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Экспериментально было установлено, что применение
схемы выравнивания вероятностей «Дельта-квадрат» с ростом скорости формирования случайных битов
не только не выравнивает вероятности генерируемых случайных битов, а наоборот – увеличивает разность вероятностей по сравнению с исходными значениями (без применения схем выравнивания).
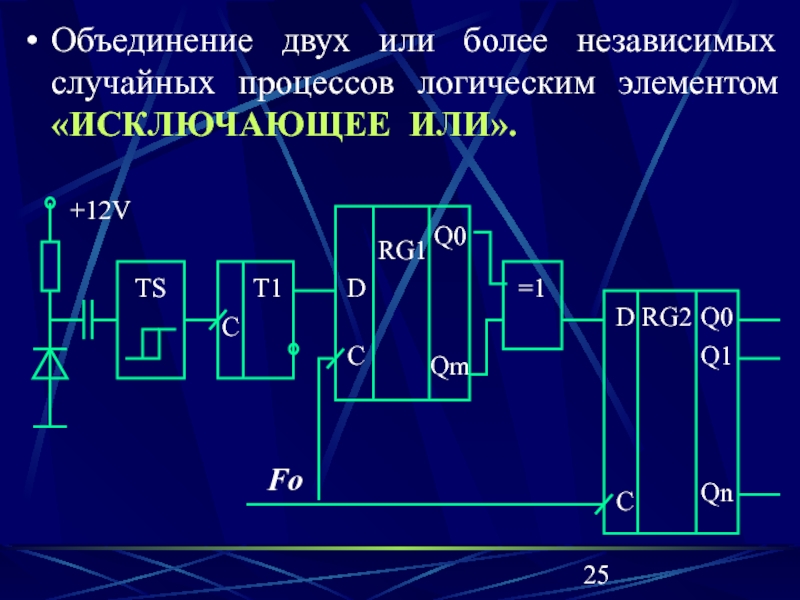
Слайд 25Объединение двух или более независимых случайных процессов логическим элементом «ИСКЛЮЧАЮЩЕЕ
ИЛИ».
Fo
TS
C
T1
+12V
Q1
Qn
Q0
RG2
D
C
Qm
Q0
RG1
D
C
=1
Слайд 27
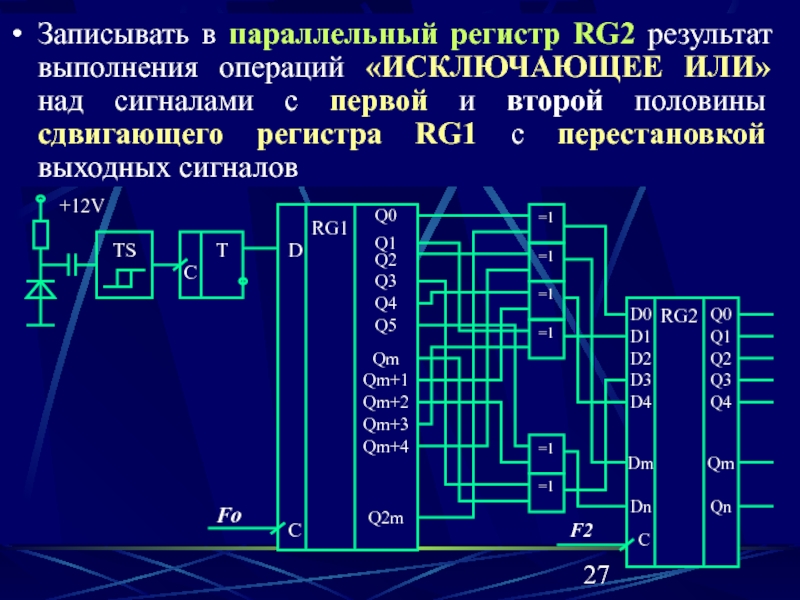
Записывать в параллельный регистр RG2 результат выполнения операций «ИСКЛЮЧАЮЩЕЕ ИЛИ»
над сигналами с первой и второй половины сдвигающего регистра RG1
с перестановкой выходных сигналов
Fo
C
TS
T
+12V
Q1
Q4
Q0
RG1
D
C
Q2
Q3
Qm
Q2m
Q1
Q4
Q0
RG2
D0
C
Q2
Q3
Qm
Qn
F2
D1
D2
D3
D4
Dm
Dn
Qm+1
Qm+2
Qm+3
=1
Qm+4
=1
=1
=1
=1
=1
Q5
Слайд 28Генератор случайных последовательностей
на основе ЛРР
Слайд 29Схему можно рассматривать как сдвигающий регистр, в который вводятся случайные
биты от источника с физическим датчиком шума, а цепь обратной
связи с элементом «ИСКЛЮЧАЮЩЕЕ ИЛИ» использу-ется для улучшения статистических свойств случай-ной последовательности по методу «Дельта-квадрат».
Эту же схему можно рассматривать как генератор псевдослучайных последовательностей на основе ЛРР, в котором в случайные моменты времени «раз-рушается рекуррента» за счет инверсии сигнала обратной связи элементом «ИСКЛЮЧАЮЩЕЕ ИЛИ», что делает такие последовательности непредсказуемыми, то есть случайными.
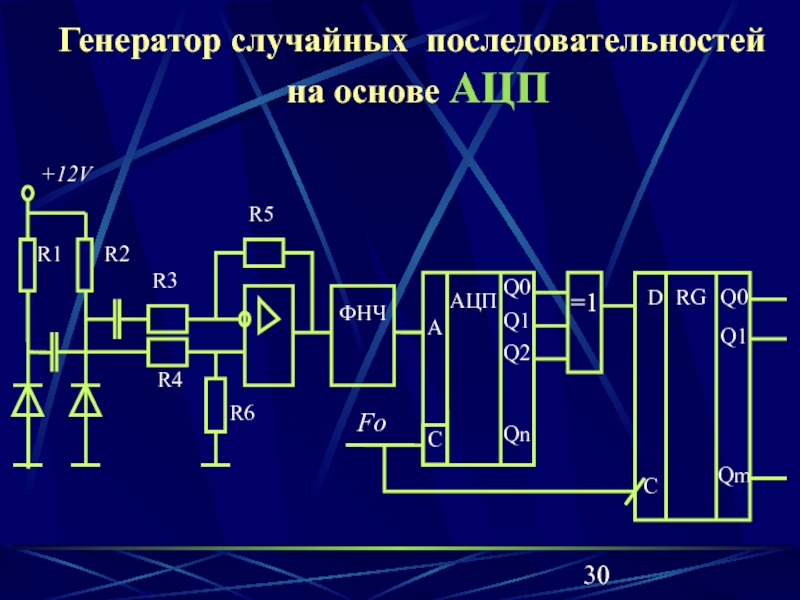
Слайд 30Генератор случайных последовательностей на основе АЦП
Слайд 31МЕТОДЫ ТЕСТИРОВАНИЯ СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ НА ОСНОВЕ МЕТОДИКИ FIPS 140-1.
Генераторы случайных
битовых последователь-ностей, реализованные на физических источниках случайности, подвергнуты влиянию внешних
факторов, а также сбоям.
Поэтому такие устройства периодически необходимо тестировать, например, с помощью статистических тестов.
Слайд 32 В этих тестах для удовлетворительных значений статистических
параметров задаются границы.
Если какой-нибудь из
тестов не пройден, то считается, что генератор (или последова-тельность) не прошел тестирование.
В американском федеральном стандарте FIPS 140-1 используются четыре статистических теста на случайность:
монобитный тест,
блочный тест,
тест серий и
тест длин серий.
Слайд 33Но в некоторых случаях тестирование случайных последовательностей необходимо производить в
аппаратном модуле генерации случайных чисел (ГСЧ) до ввода в ПЭВМ.
Для этих целей обычно применяют одно-кристальные микро-ЭВМ (ОМЭВМ) – микроконтроллеры (МК).
Алгоритм тестирования FIPS 140-1 может быть реализован на программном уровне после ввода последовательности s – 20000 случайных бит в ПЭВМ.
Слайд 34Для того, чтобы достоверно измерить разность вероятностей Р(1)-Р(0)=10-12, необходимо сгене-рировать
случайную битовую последовательность длиной не менее 1024 бита.
При частоте
генерации случайных битовых последовательностей 16 Мбит/с для этого понадобится более 1 000 000 000 лет.
Слайд 35Вопросы для экспресс-контроля
Назовите основные отличия случайных последовательностей от псевдослучайных.
Назовите методы
генерации псевдослучайных последовательностей.
Назовите основные источники физического шума для генерации
случайных последовательностей.
Перечислите основные тесты американского стандарта тестирования случайных последователь-ностей FIPS 140-1.
Назовите методы выравнивания вероятностей случайных битовых последовательностей.
Слайд 36Лекция окончена
Спасибо за внимание