Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Анализ взаимосвязи социально-экономических явлений
Содержание
- 1. Анализ взаимосвязи социально-экономических явлений
- 2. Источники получения
- 3. Источники получения
- 4. Источники получения
- 5. Спецификация модели
- 6. Спецификация модели
- 7. Графическое изображение
- 8. Метод наименьших
- 9. Построение уравнения регрессии
- 10. Метод наименьших
- 11. Метод наименьших
- 12. Метод наименьших
- 13. Метод наименьших
- 14. Метод наименьших
- 15. Скачать презентанцию
Источники получения данных Социально-экономические явления представляют собой результат одновременного воздействия большого числа причин. При изучении этих явлений следует выделить следующие этапы.1. Качественный анализ связей
Слайды и текст этой презентации
Слайд 1Анализ взаимосвязи социально-экономических явлений
Этапы исследования взаимосвязей между явлениями
Функции и характеристики
документа
Слайд 2
Источники получения данных
Социально-экономические явления представляют собой результат
одновременного воздействия большого числа причин.
При изучении этих явлений следует
выделить следующие этапы.1. Качественный анализ связей экономических переменных — выделение зависимых Си) и независимых (х).
2. Подбор данных.
3. Спецификация (установление) формы связи между у и х.
4. Оценка параметров модели.
Слайд 3
Источники получения данных
Признаки по их значению для
изучения взаимосвязи делятся на два класса.
Признаки, обусловливающие изменение других
связанных с ними признаков, называют факторными или просто факторами (х). Признаки, изменяющиеся под действием факторных признаков, называют результативными (у).
Различают функциональную связь и стохастическую зависимость. Функциональной называют такую связь, при которой определенному значению факторного признака соответствует только одно значение результативного признака.
Слайд 4
Источники получения данных
Если причинная зависимость проявляется
не в каждом отдельном случае, а в общем при большом
числе наблюдений, то такая зависимость называется стохастической.По направлению выделяют связь прямую и обратную.
По аналитическому выражению выделяют связи прямолинейные и нелинейные (криволинейные).
Слайд 5
Спецификация модели
Исследование социально-экономических явлений начинается с
теории, устанавливающей связь между явлениями, т. е. со спецификации
модели.Спецификация модели — это формулировка вида модели исходя из соответствующей связи между переменными.
В зависимости от количества факторов, включенных в уравнение регрессии, принято различать парную и множественную регрессии.
Парная регрессия характеризует связь между двумя признаками: результативным и факторным.
Слайд 6
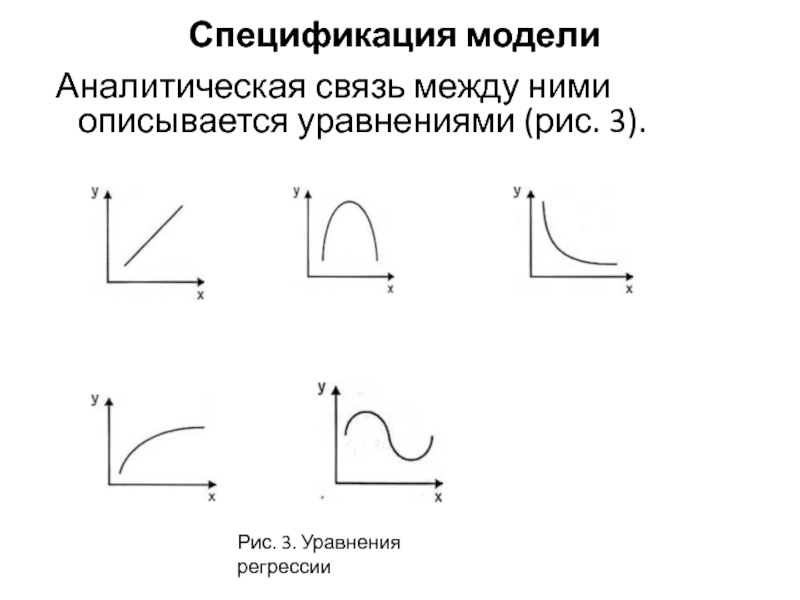
Спецификация модели
Аналитическая связь между ними описывается
уравнениями (рис. 3).
Рис. 3. Уравнения регрессии
Слайд 7
Графическое изображение параметров уравнения
Если результативный и факторный
признаки возрастают одинаково, примерно в арифметической прогрессии, то это свидетельствует
о наличии линейной связи между ними,а при обратной связи — гиперболической.
Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая или степенная функции.
Слайд 8
Метод наименьших квадратов
Классический подход по оцениванию
параметров линейной регрессии основан на МНК.
Линейная регрессия сводится к нахождению
уравнений вида:о- = о0 +atx.
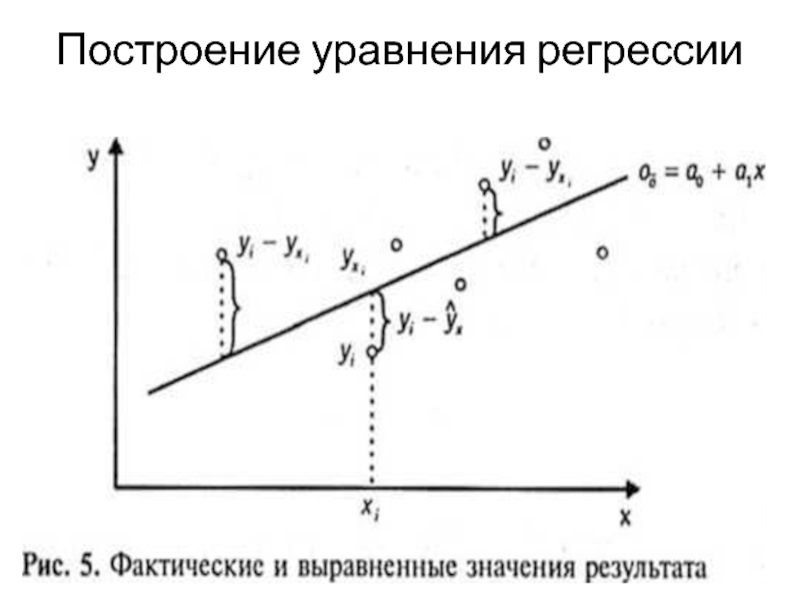
Построение уравнения регрессии сводится к оценке ее параметров а0 и а\.
В основе этого метода лежит предположение о независимости наблюдений исследуемой совокупности, при которой сумма квадратов отклонений эмпирических значений от теоретических значений результативного признака стремится к нулю;
S = Z(y, -УхУ ->mіn.
Так как о5 = а0 + а}х, то получим:
■* = Х<Уі -У*)2 =ХО'-«о -*)2;
Слайд 10
Метод наименьших квадратов
После преобразования получим следующую
систему нормальных уравнений:
Гл-во + я.Е* = Е->'
|а0 -£х + а,
-Z*2Решая систему нормальных уравнений, найдем параметры а о и Q\.
ай =у-а, х , со ѵ(х,у)
Параметр а\ называется коэффициентом регрессии. Его величина показывает среднее изменение результата при изменении фактора на одну единицу.
Так, если в функции издержек: у = 15 + 1,2 х
(у — издержки,
х — количество произведенной продукции, тыс. шт., тыс. руб.), то, с увеличением объема продукции на 1 тыс. шт. издержки производства вырастут в среднем на 1,2 тыс. руб.,
Слайд 11
Метод наименьших квадратов
Значимость коэффициента регрессии осуществляют
с помощью /-критерия Стьюдента:
где G] — дисперсия коэффициента регрессии.
Параметры
модели признаются значимыми, если /р > /кр (/кр — уровень значимости
wV=n-k-\ — число степеней свободы,
где к — число факторов признаков).
Значение средней ошибки аппроксимации определяется по формуле
Оно не должно превышать 12—15%.
Слайд 12
Метод наименьших квадратов
Для статистической оценки тесноты
связи применяются следующие показатели вариации:
1) общая дисперсия результативного признака а2у, отображающая
общее влияние всех факторов:п
2) факторная дисперсия результативного признака а2у,, отображающая вариацию у только от воздействия изучаемого фактора х.
Юч -У)1
п
Данная формула характеризует отклонение выравненных значений ух от их общей средней величины у\
Слайд 13
Метод наименьших квадратов
3) остаточная дисперсия а2с, отображающая
вариацию результативного признака у от всех прочих, кроме х, факторов:
п
Данная формула характеризует отклонения эмпирических (фактических) значений результативного признака у\ от их выравненных значений ухГ
Слайд 14
Метод наименьших квадратов
Соотношение между факторной и
общей дисперсиями характеризует меру тесноты связи между признаками х и
у:Показатель R2 называется индексом детерминации (причинности).
Он выражает долю факторной дисперсии в общей дисперсии, т. е. характеризует, какая часть общей вариации результативного признака у объясняется изменением факторного признака х.
На основе предыдущей формулы определяется индекс корреляции R: с.145