Арифметические комбинационные схемы

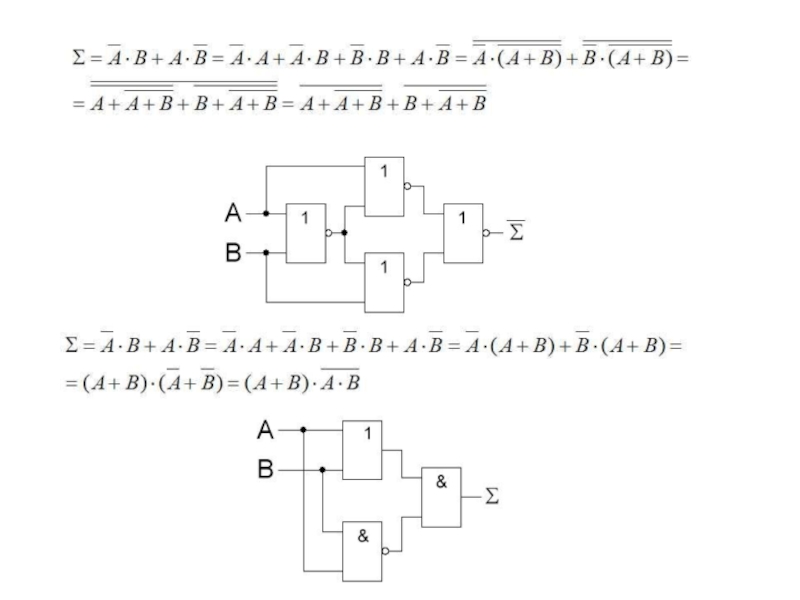
n-разрядных чисел (слов).
На базе сумматора можно реализовать другие арифметические

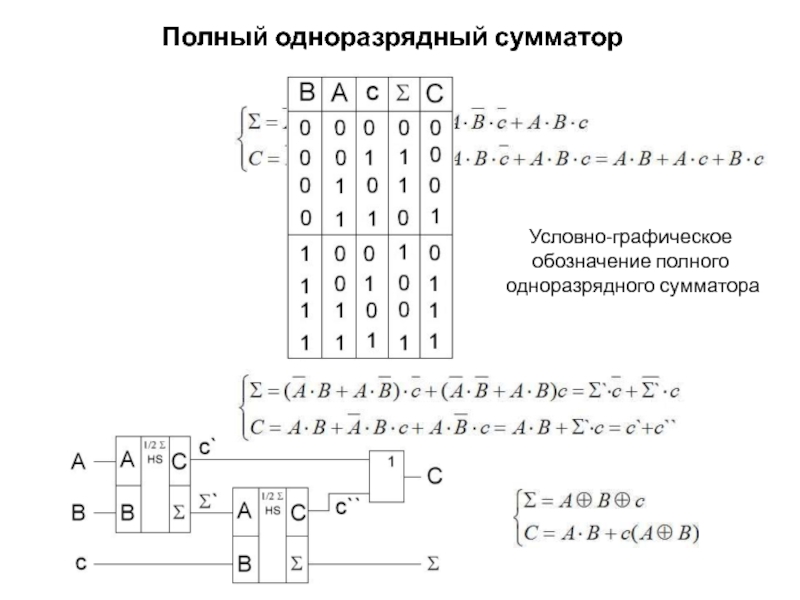
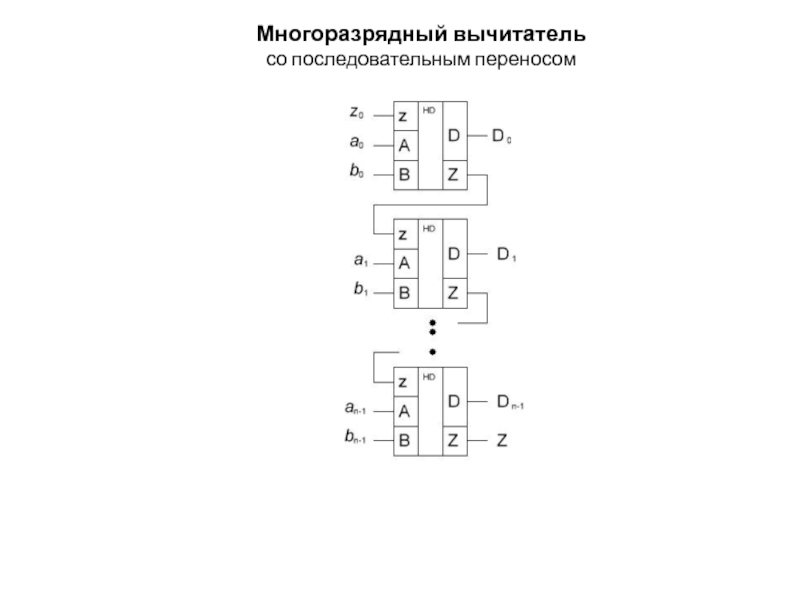
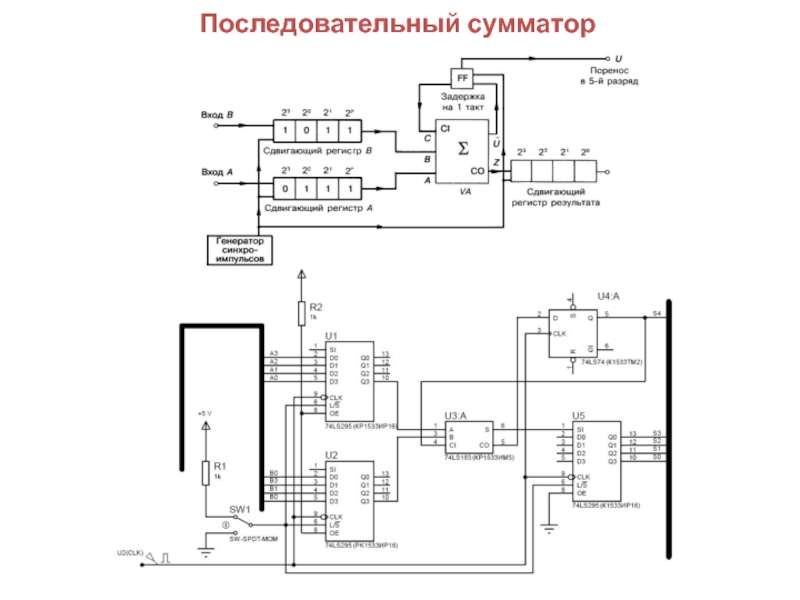
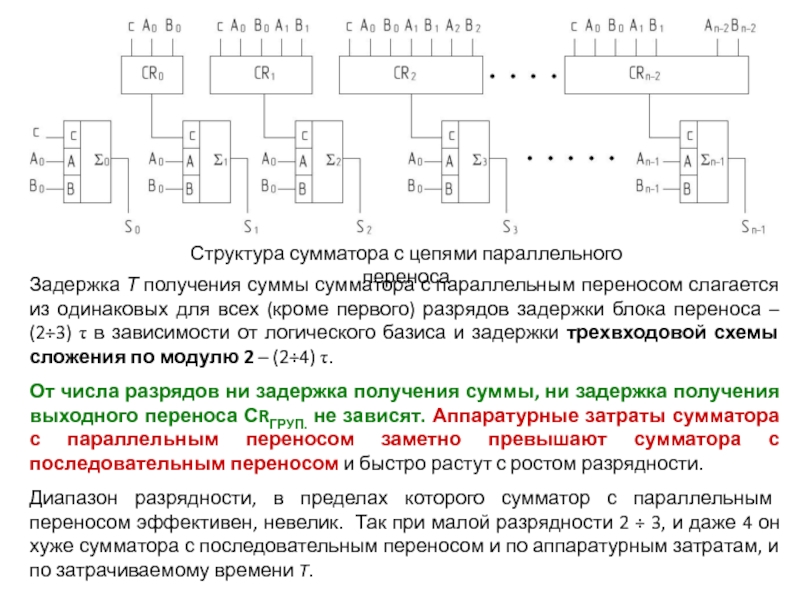
операции:

Многоразрядный двоичный сумматор состоит из отдельных схем, которые называются одноразрядными двоичными сумматорами; они выполняют все действия по сложению значений одноименных разрядов двух чисел (операндов).

Поэтому сумматор является важнейшей частью любого арифметико-логического устройства (АЛУ).
Функция сумматора на его условно-графическом обозначении (УГО) на принципиальной электрической схеме обозначается буквами SM или S.

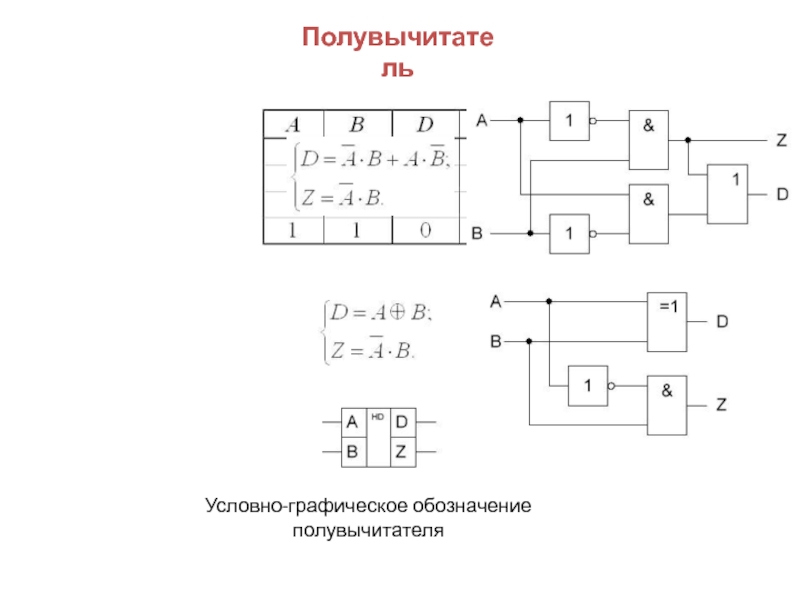
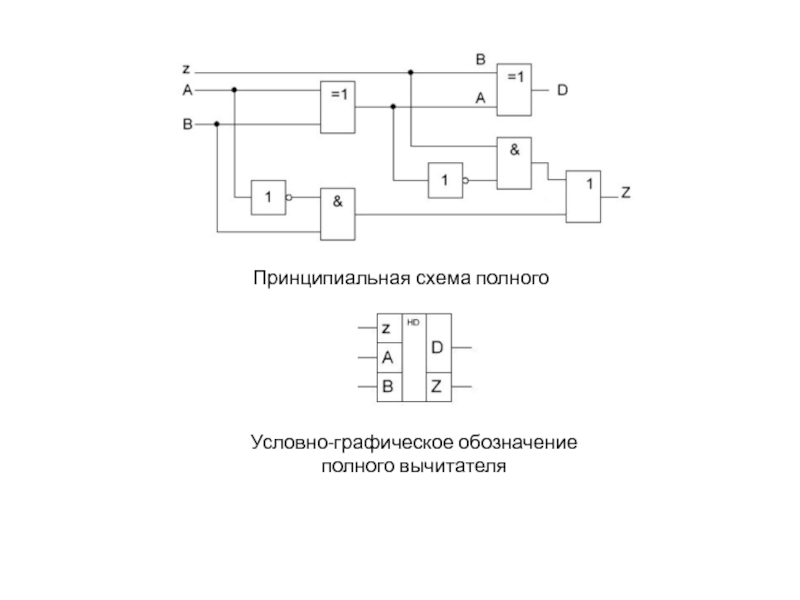
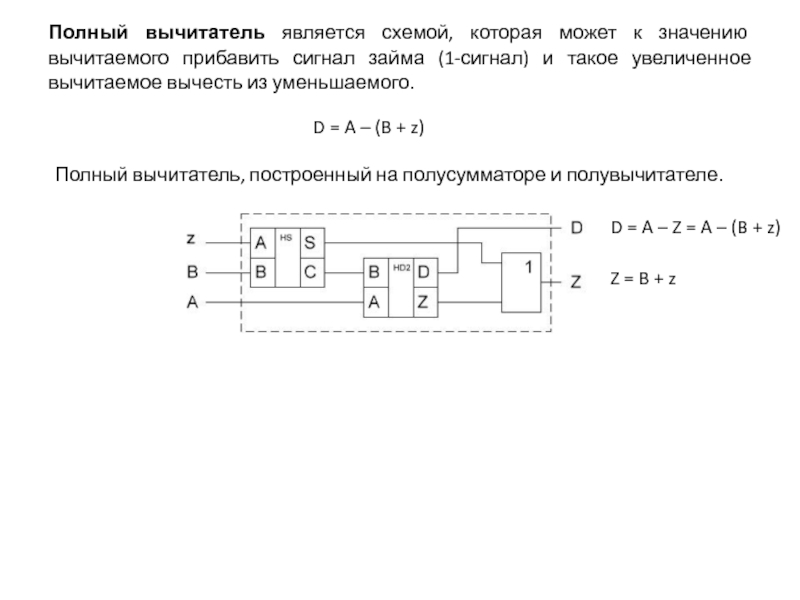
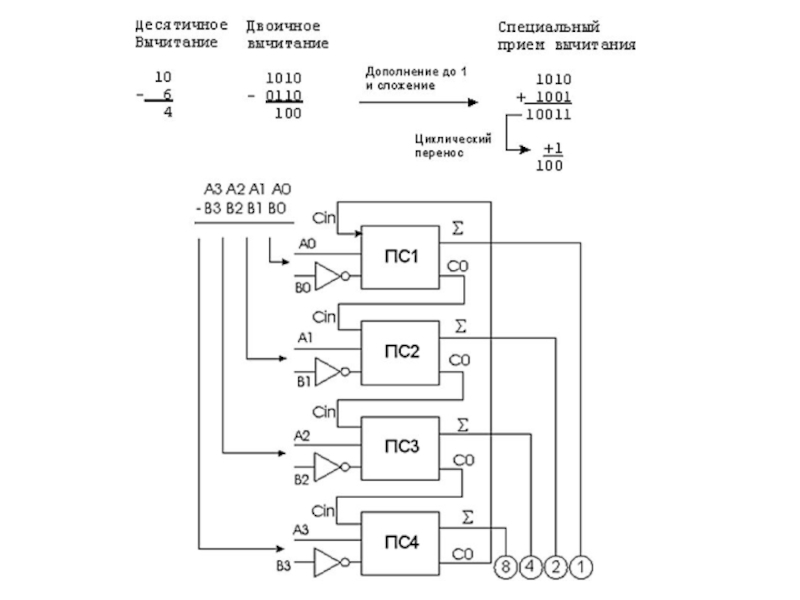
Операция вычитания заменяется сложением чисел представленных в обратном или дополнительном коде.
Операции умножения и деления сводятся к реализации операций многократных сложений и сдвигов.

параллельно-последовательные;
числу входов – одноразрядные и многоразрядные сумматоры;
организацией хранения результата сложения

– комбинационные, накапливающие, комбинированные;
организацией цепей переноса между разрядами – с последовательным, параллельным или комбинированным переносом (с групповой структурой);
системой счисления – позиционные (двоичные, двоично-десятичные) и непозиционные (код Грея, избыточные коды);
разрядностью (длиной) операндов – 8-, 16-, 32-, 64-разрядные;
способом представления отрицательных чисел – в обратном или дополнительном кодах, а также в их модификациях;
временем сложения – синхронные, асинхронные.

начала подачи операндов на входы сумматора до получения результата суммирования

на его выходах Часто быстродействие характеризуется количеством сложений в секунду FS = 1/tS (имеются в виду операции типа регистр-регистр, это когда числа хранятся в регистрах АЛУ);
аппаратурными затратами – когда стоимость одноразрядной схемы сложения определяется общим числом логических входов используемых элементов; стоимость многоразрядного сумматора определяется общим количеством используемых микросхем;
потребляемой мощностью сумматора.

Сумматоры характеризуются следующими параметрами:

(xn-1 , ... ,x0 ) – 1-e cлaгaeмoe
+

Y = (yn-1 , ... ,y0 ) – 2-e cлaгaeмoe
---------------------------------------
S = (sn, sn-1, ... ,s0 ) – cyммa

Пpaвилa cлoжeния двyx oднopaзpядныx двoичныx чиceл,
где "+" – арифметическое сложение:
0 + 0 = 0
0 + 1 = 1 + 0 = 1
1 + 1 = 0 и пepeнoc 1 в cтapший paзpяд.

Уcтpoйcтвo peaлизyющee эти пpaвилa нaзывaeтcя oднopaзpядным
пoлycyммaтopoм и имeeт двa вxoдa и двa выxoдa.

Пpaвилa слoжeниe тpex однopaзpядныx чиceл пpoизвoдитcя cлeдyющим oбpaзoм, где "+" – арифметическое сложение:
0 + 0 + 0 = 0
0 + 0 + 1 = 1
0 + 1 + 1 = 0 и пepeнoc 1 в cтapший paзpяд
1 + 1 + 1 = 1 и пepeнoc 1 в cтapший paзpяд.

Уcтpoйcтвo peaлизyющee эти пpaвилa нaзывaeтcя oднopaзpядным
пoлным cyммaтopoм и имeeт три вxoдa и двa выxoдa.

ЛП12

КМОП – ИС типа ЛП2 (561, 564)

ЛП12 (1561)

для многоразрядного вычитания.
Полный вычитатель может строится на двух полувычитателях.
В

полувычитателе HD1 сначала образуется разность А – В.
Полувычитателем HD2 вычитается заем z полученный в предыдущем разряде от результата вычитания полученного в HD1.
При осуществлении займов как при вычитании в HD1 так и при вычитании в HD2 на выходе Z появляется сигнал 1.

A – (B + z)
Полный вычитатель, построенный на полусумматоре и

полувычитателе.

Полный вычитатель является схемой, которая может к значению вычитаемого прибавить сигнал займа (1-сигнал) и такое увеличенное вычитаемое вычесть из уменьшаемого.

D = A – (B + z)

компьютера, были предприняты усилия по сведению к одному алгоритму процедуры

вычитания и сложения. Этого можно добиться, если применять двоичные цифры в их дополняющей форме.
Различают:
а) единичное дополнение (one's complement) и
(обратный код, поразрядное дополнение)
1001100111 → 0110011000
б) двойное дополнение (two's complement) (точное дополнение).
11011101011 → 00100010100 + 1 → 00100010101

Дополняющие формы представление двоичных чисел

Если вычитаемое больше, чем уменьшаемое, т.е. В > A, то возникающее отрицательное число представляется в выходном регистре неправильно.
Для правильного представления оно должно дополняться, то есть в случае отрицательного результата его инвертируют и прибавляют 1.

равно числу разрядов слагаемых.

По характеру распространения переноса различают следующие виды

сумматоров:

с поразрядным последовательным переносом;
с параллельным одновременным переносом;
с групповым переносом.

с параллельным переносом слагается из одинаковых для всех (кроме первого)

разрядов задержки блока переноса – (2÷3) t в зависимости от логического базиса и задержки трехвходовой схемы сложения по модулю 2 – (2÷4) t.
От числа разрядов ни задержка получения суммы, ни задержка получения выходного переноса СRГРУП. не зависят. Аппаратурные затраты сумматора с параллельным переносом заметно превышают сумматора с последовательным переносом и быстро растут с ростом разрядности.
Диапазон разрядности, в пределах которого сумматор с параллельным переносом эффективен, невелик. Так при малой разрядности 2 ÷ 3, и даже 4 он хуже сумматора с последовательным переносом и по аппаратурным затратам, и по затрачиваемому времени T.

в сумматорах с большим числом разрядов применяют принцип группового переноса.

Сумматор разбивают на группы, представляющие собой небольшие сумматоры с разрядностью обычно от 2 до 8.
Блоки переноса анализируют слагаемые, т.е. определяют состояние группы и если из группы должен быть перенос, то он появляется на выходе блока для подачи его на вход следующей группы и в цепочку распространения переноса от младшей группы к старшей. Тракт группового переноса построен так, что время распространения переноса в нем между группами оказывается меньше, чем если бы этот перенос распространялся по цепям внутригрупповых трактов
Переносы в группе определяются по формулам как для обычных сумматоров с параллельным переносом, но сами сумматоры благодаря делению на группы существенно упрощаются, т.к. у них все блоки формирования переноса имеют одинаковую сложность, тогда как в сумматоре с параллельным переносом сложность схем переноса возрастает непрерывно от предыдущего разряда к последующему.

случай сумматора с групповым переносом, когда разрядность каждой группы равна

1, тракт межгруппового переноса может быть построен:

Параллельный перенос между группами в сочетании с параллельным переносом внутри группы дает самые быстрые сумматоры в диапазоне разрядности, приблизительно от 24 до 64. Задержка таких параллельно-параллельных сумматоров не зависит от разрядности и составляет (9÷10)t в зависимости от используемого логического базиса. За скорость приходится платить, и аппаратурные затраты таких сумматоров заметно превышают затраты сумматоров с другими типами переносов.

В диапазоне разрядности примерно от 8 до 24 первенство по скорости переходит к сумматорам с параллельным переносом между группами и с последовательным внутри групп. Разрядность групп при этом выбирают небольшой – от 2 до 4.

как параллельным, когда все групповые переносы вырабатываются параллельно как функции только слагаемых,
так и последовательным, когда исходным материалом для переноса в каждую следующую группу служит перенос, поступающий на вход данной группы.

базовое число.
Множитель является числом, на которое увеличивается множимое. В

результате получается произведение.

Множимое Множитель Произведение
2 х 3 = 6

Параллельные умножители

Например, перемножим два двухразрядных двоичных числа: 2∙3 = 6

102
112
102 —> 1-е слагаемое
102 —> 2-е слагаемое
1102 —> Результат

Элемент И является 1-битовым умножителем

Сложение происходит в 2-битовом параллельном сумматоре. И-элементы должны быть включены

таким образом, чтобы второе слагаемое прибавлялось к первому слагаемому со смещением на одну позицию влево.

Пример: 2 ∙ 3 = 6