ЧИСЛА ФИБОНАЧЧИ # БЕСЕДУЮТ МАТЕМАТИКИ 20.11.2019

известна стала при жизни ее основного исследователя – Леонардо Пизанского,

более известного, как Фибоначчи (1202 год).

Он рассматривал применение этой последовательности в задаче об идеализированной паре кроликов, о которой дальше…

Формула последовательности:
Fn+Fn+1=Fn+2

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987…

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

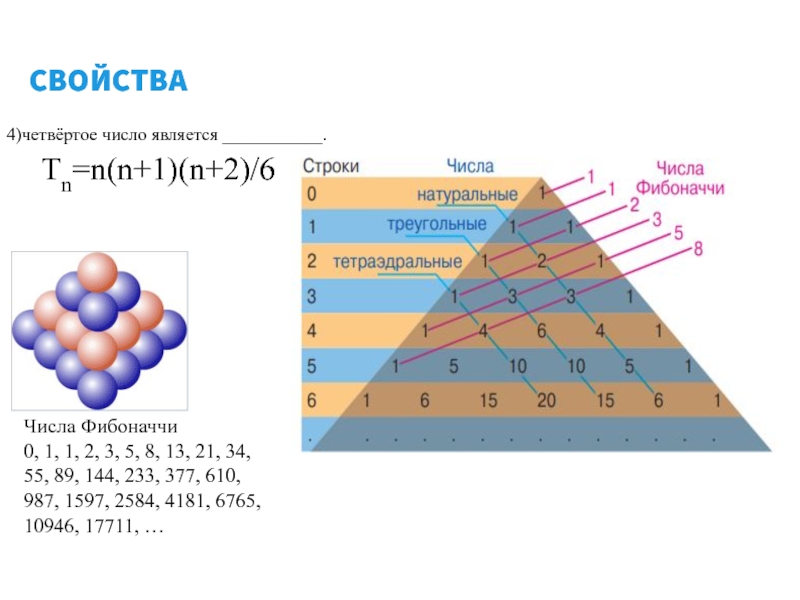
Числа Фибоначчи

– со второго месяца жизни они производят новую пару кроликов

– тоже самку и самца. Кролики находятся в замкнутом пространстве и постоянно размножаются. И ни один кролик не умирает.
Вопрос:
Определить количество кроликов через год.

Задача про кроликов

которая спаривается в конце месяца

Две пары кроликов во втором месяце

(первая пара и потомство)

Три пары кроликов в третьем месяце (первая пара, потомство первой пары с прошлого месяца и новое потомство)

Пять пар кроликов в четвёртом месяце (первая пара, первое и второе потомство первой пары, третье потомство первой пары и первое потомство второй пары)

Из этого следует, сто количество кроликов в месяц «n» = количеству кроликов прошлого месяца + количество новых пар кроликов, то есть, формула: Fn+Fn+1=Fn+2.

Так как спрашивается, сколько кроликов будет через год, в качестве ответа будет 14 число последовательности (не учитывается в задаче первое число –1), 377 (пар), т.е. 754 кролика.

89, 144, 233, 377, 610, 987…
1 2 3

4 5 6 7 8 9 10 11 12 13 14 15 16

1. А если сложить все члены последовательности с нечетными индексами ?

Если сложить все члены последовательности , то легко можно вычислить их сумму

2. А если сложить все члены последовательности с четными индексами ?

Числа Фибоначчи. Свойства

Символическая запись

(Fn)2+(Fn+1)2+2(Fn*Fn+1)=____
1 2 3 4 5

6 7 8 9 10 11 12 13 14 15 16

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987…

множество неожиданных и интересных свойств.

писатель и религиозный философ

сумме всех чисел, расположенных внутри параллелограмма,
который ограничен левыми и

правыми диагоналями, пересекающимися на этом числе.

ряда – натуральный ряд.
3. Сумма чисел n-й строки треугольника Паскаля

равна ___
4.Все числа в n-й строке, кроме единиц, делятся на число n, тогда и только тогда, когда n является ___________.
5.Любой элемент из треугольника Паскаля, уменьшенный на единицу, равен сумме всех чисел, расположенных внутри параллелограмма, который ограничен левыми и правыми диагоналями, пересекающимися на этом числе.
6.В каждой строке сумма чисел на четных местах равна сумме ___________

______
2)второе и предпоследнее числа ______
3)третье число равно треугольному числу Tn=n(n+1)/2

4)четвёртое число является ___________.

Tn=n(n+1)(n+2)/6

Треугольные числа
0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 221, 243, 266, 290 …

34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584,

4181, 6765, 10946, 17711, …

4)четвёртое число является ___________.

Tn=n(n+1)(n+2)/6

номером соседнее число из той же строки, то получится число

Каталана.

Количество разбиений выпуклого (n+2)-угольника на треугольники непересекающимися диагоналями.
Количество способов соединения 2n точек на окружности n непересекающимися хордами.
Количество правильных скобочных последовательностей длины 2n

треугольник Серпинского.
ТРЕУГОЛЬНИК СЕРПИНСКОГО

ребенок. В то же время он таит в себе неисчерпаемые

сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике.
Мартин Гарднер

N-мерный Коля