линейных алгебраических уравнений,
решение систем обыкновенных дифференциальных уравнений,
решение уравнений
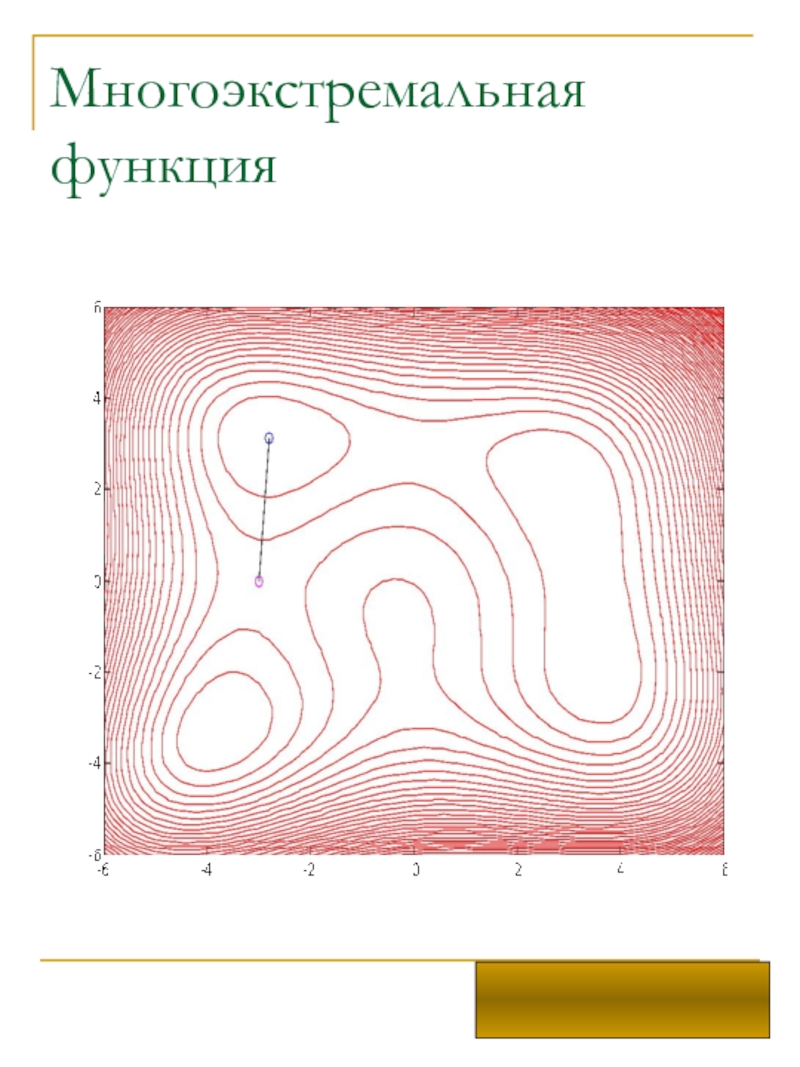
в частных производных,оптимизация,
обработка числовых данных.
Алгоритмы типа «разделяй-и-властвуй» реализуются в задачах поиска корня алгебраических и трансцендентных уравнений, а также в задачах оптимизации.

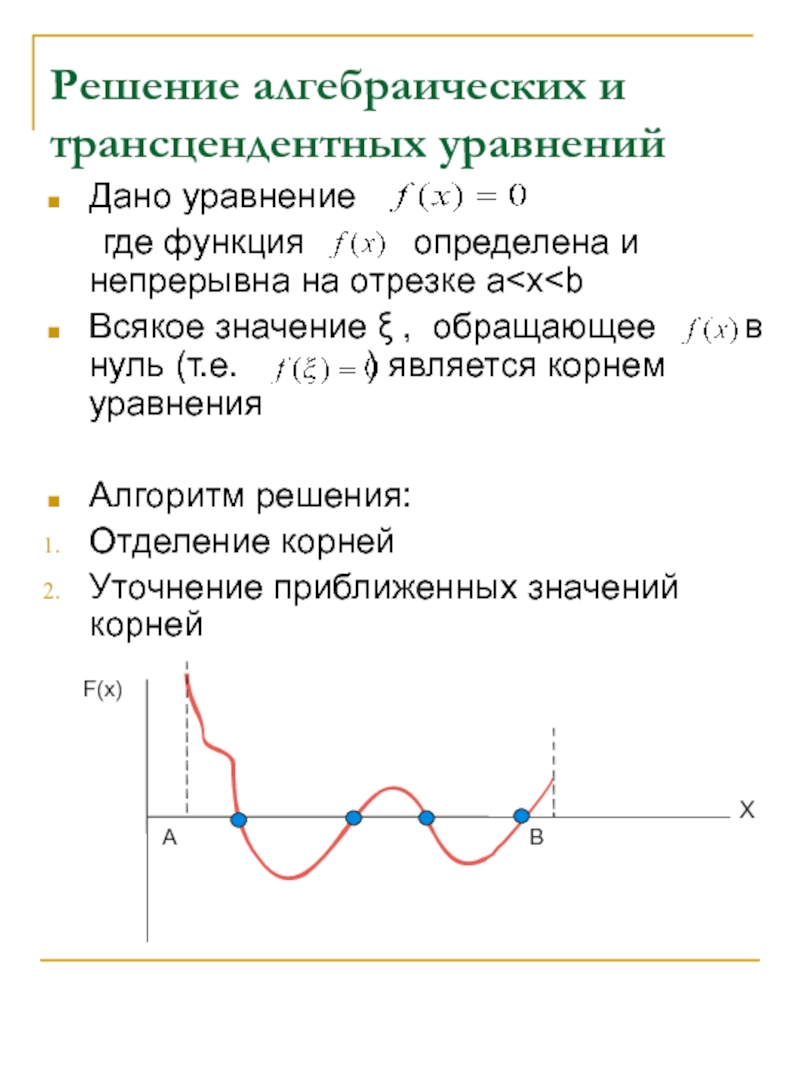
![Численные алгоритмы Отделение корней производится разбиением интервала [a,b] на участки [a - x1 Отделение корней производится разбиением интервала [a,b] на участки [a - x1 - x2 - x3- … -](/img/thumbs/84bb50c3bebbbba48dc820c3c530752a-800x.jpg)
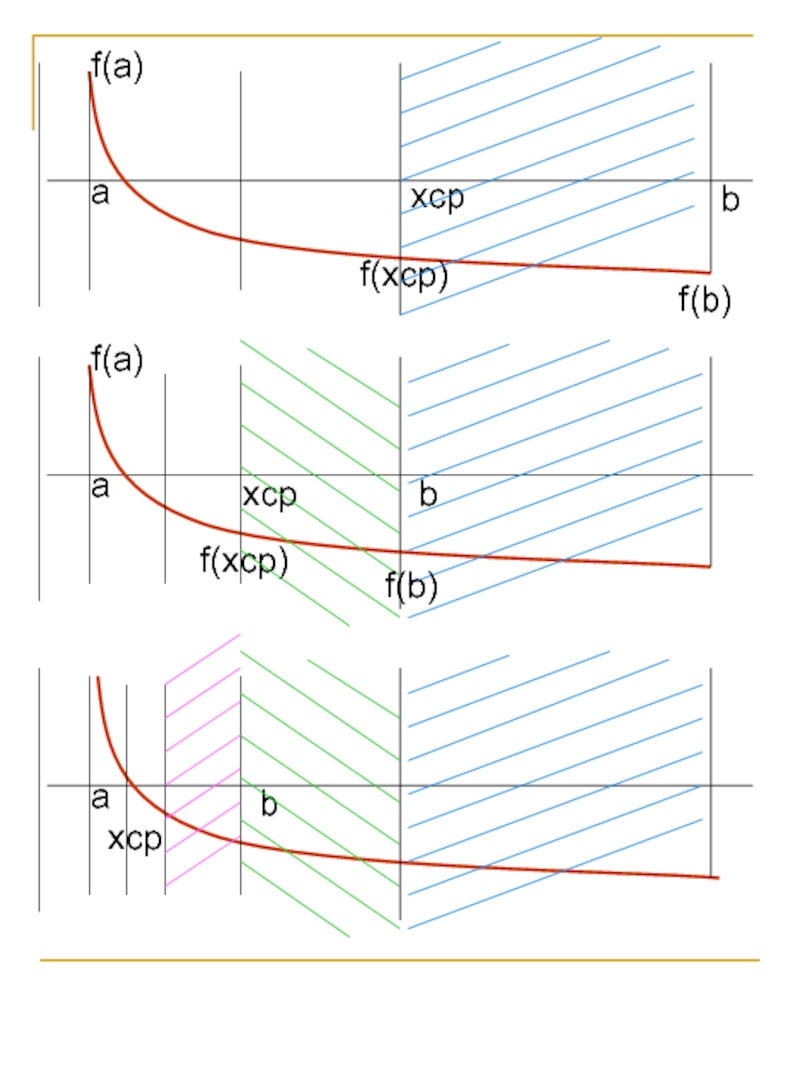
![Численные алгоритмы Корень нелинейного уравнения. Деление отрезка пополам. Функция f(x) задана на отрезке Корень нелинейного уравнения. Деление отрезка пополам. Функция f(x) задана на отрезке [a,b] и имеет только один корень](/img/thumbs/eff17a480d6ece0e65db54ad725d1f48-800x.jpg)

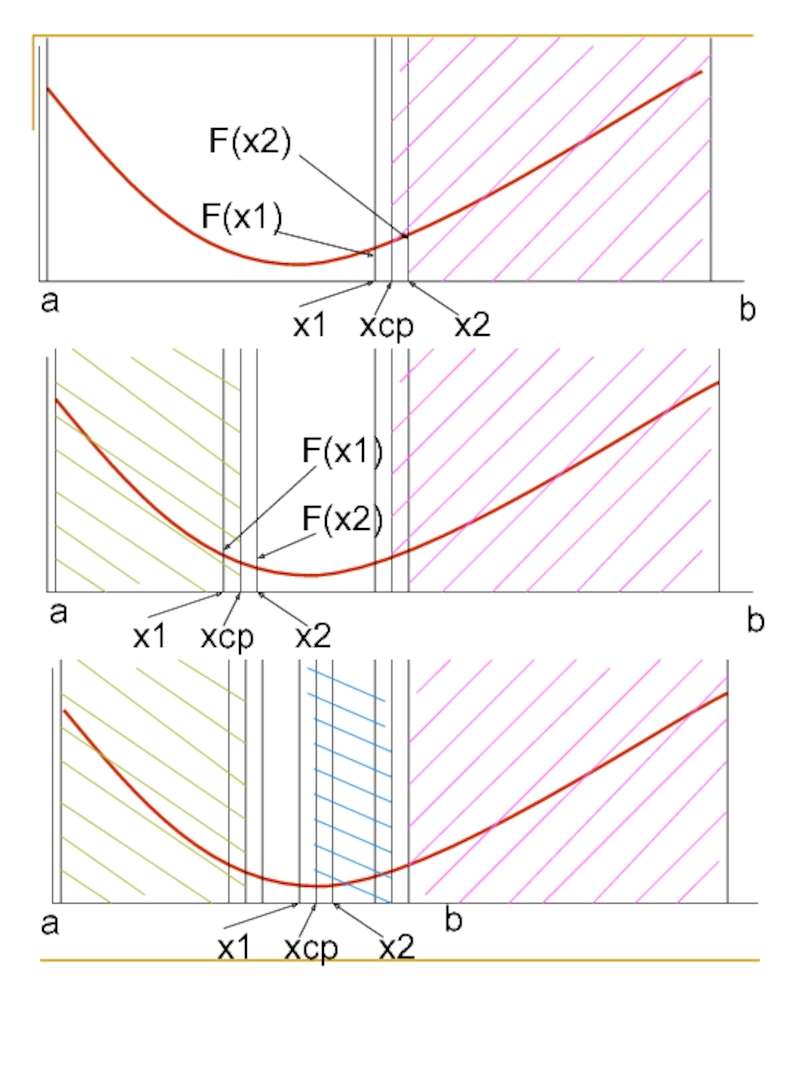
![Численные алгоритмы Поиск минимума функции одной переменной: дихотомия Функция F(x) задана на отрезке [a,b] Поиск минимума функции одной переменной: дихотомия Функция F(x) задана на отрезке [a,b] и имеет только один минимум. ε,](/img/thumbs/f8015f1eb47508efc5398dfaebf86ae8-800x.jpg)
![Численные алгоритмы Функция F(x) задана на отрезке [a,b] и имеет один минимум. ε, Функция F(x) задана на отрезке [a,b] и имеет один минимум. ε, δ – малые значения , b>a.Поиск](/img/thumbs/de8ed9138dd9d4ea88a862d7ecb97710-800x.jpg)

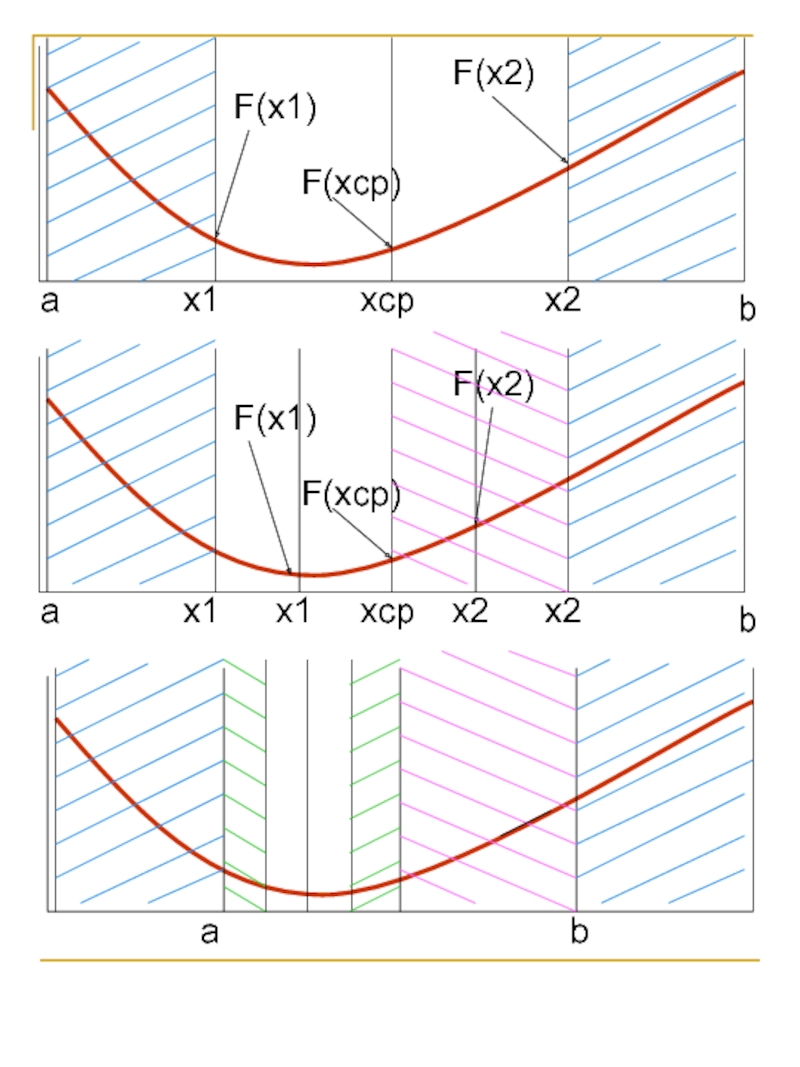

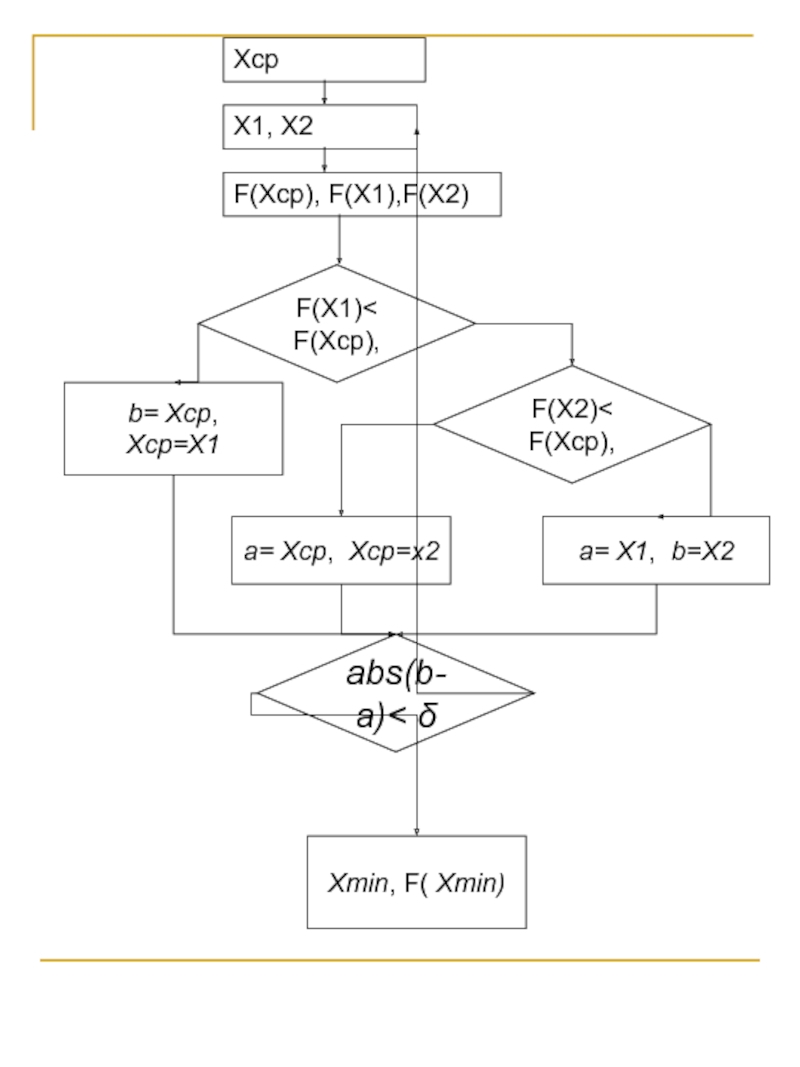

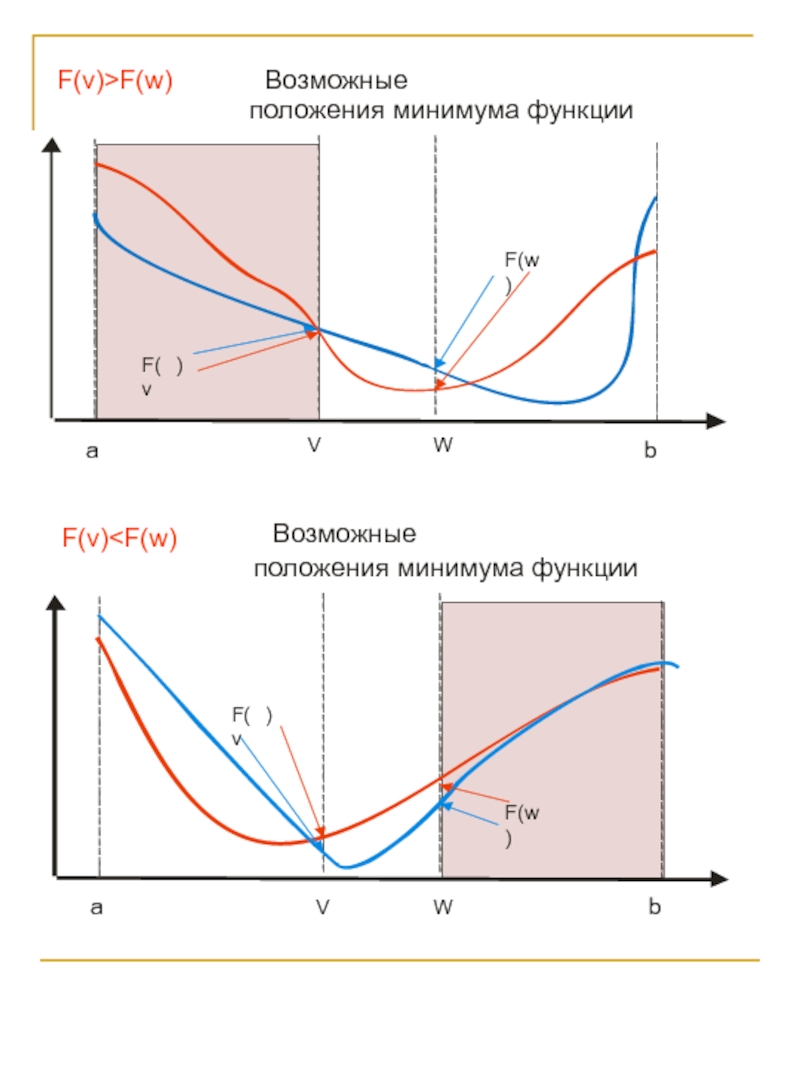
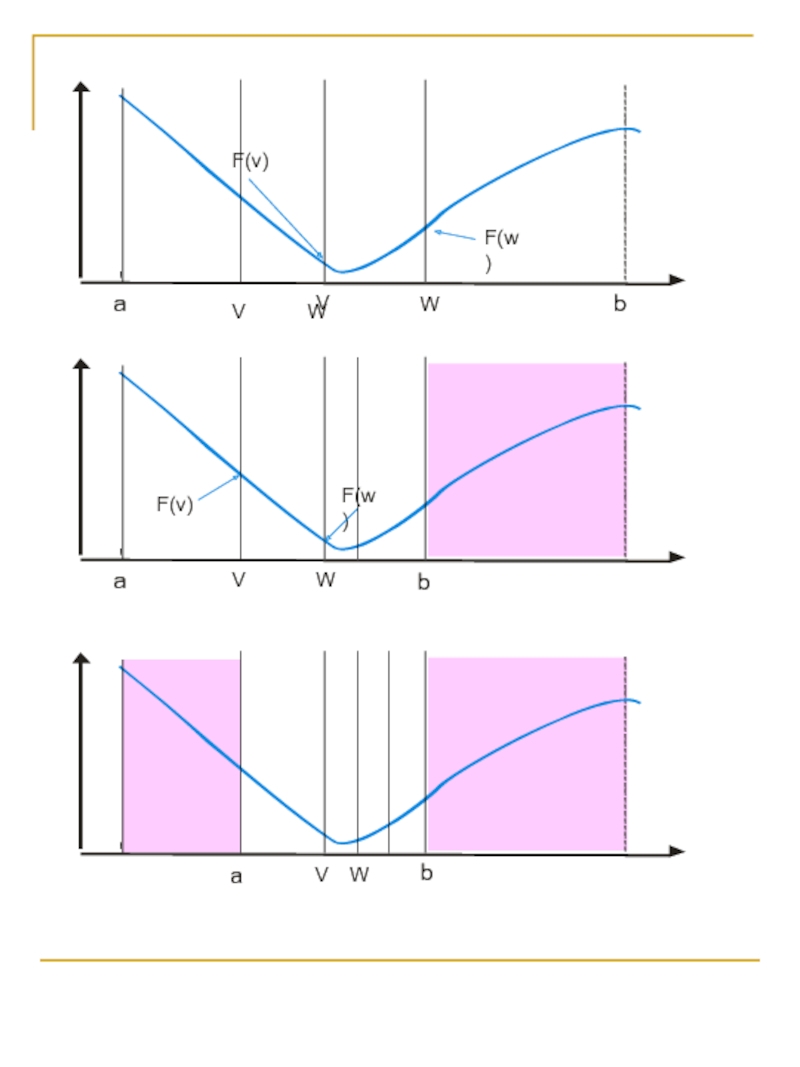
![Численные алгоритмы Шаг1: Задаем коэффициенты k2=0.62, k1=0.38, интервал [a,b] и отрезок L=b-a.Шаг2: Выделяем Шаг1: Задаем коэффициенты k2=0.62, k1=0.38, интервал [a,b] и отрезок L=b-a.Шаг2: Выделяем две точки на оси аргументов v=L*k1](/img/thumbs/f85205b16a8c25b3aa73d5a8dc8eced6-800x.jpg)