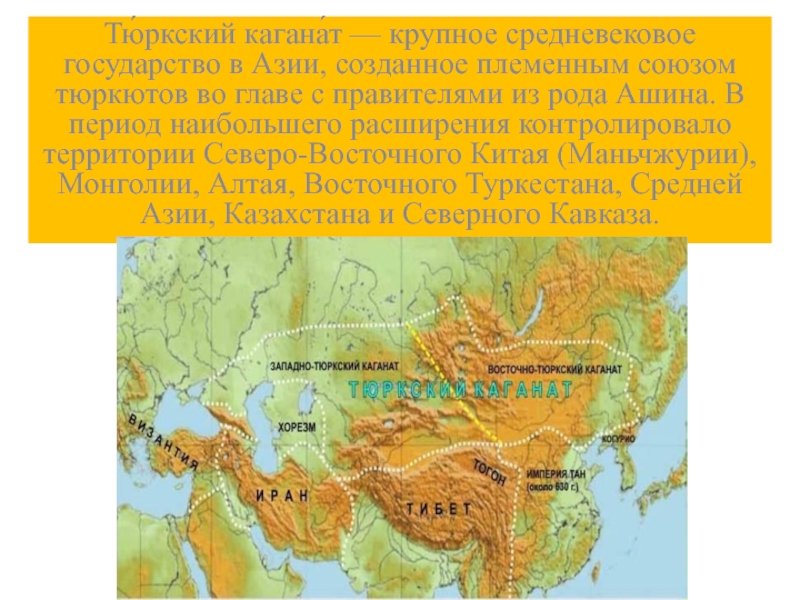
к
которому добавляют одно и то же число. Это
число для данной
последовательности называютразностью и обозначают d.
(АП) бывает: возрастающей, если разность d>0; убывающей, если d<0;