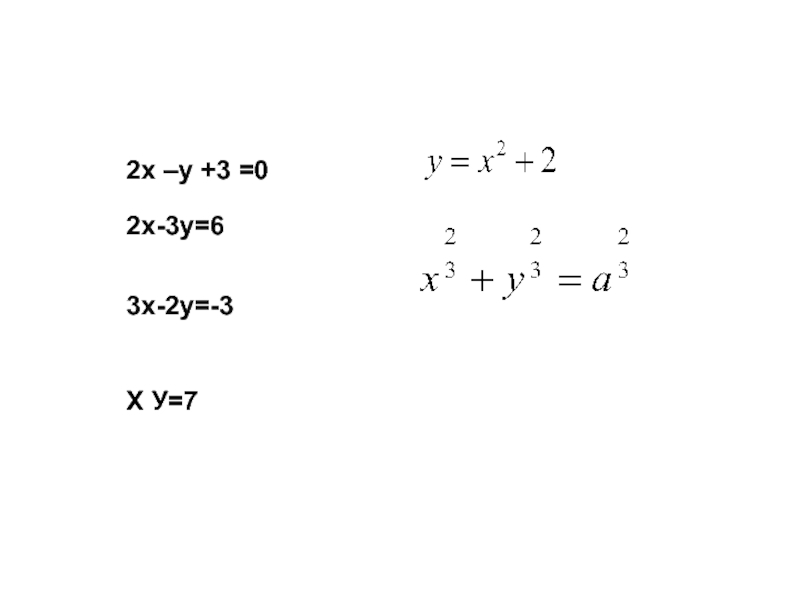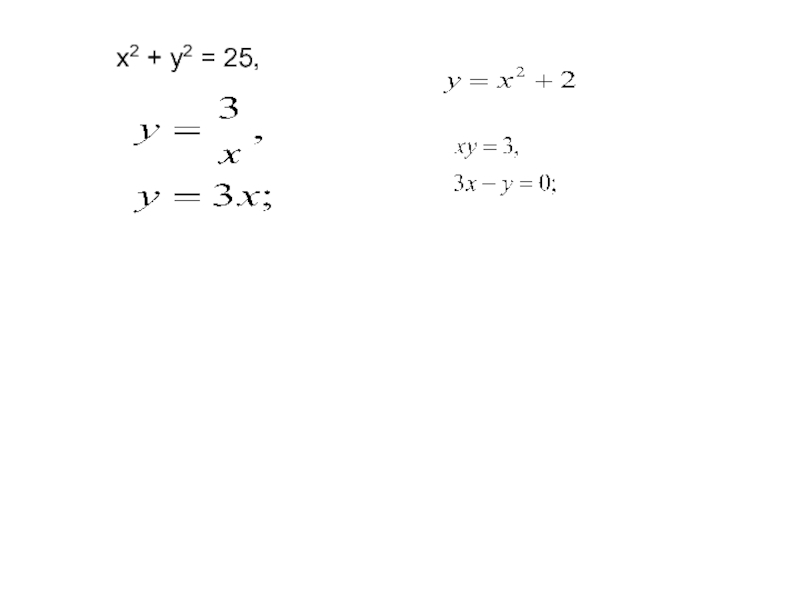Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что значит графически решить систему уравнений?
Содержание
- 1. Что значит графически решить систему уравнений?
- 2. Что значит графически решить систему уравнений?
- 3. 2х –у +3 =02х-3у=63х-2у=-3Х У=7
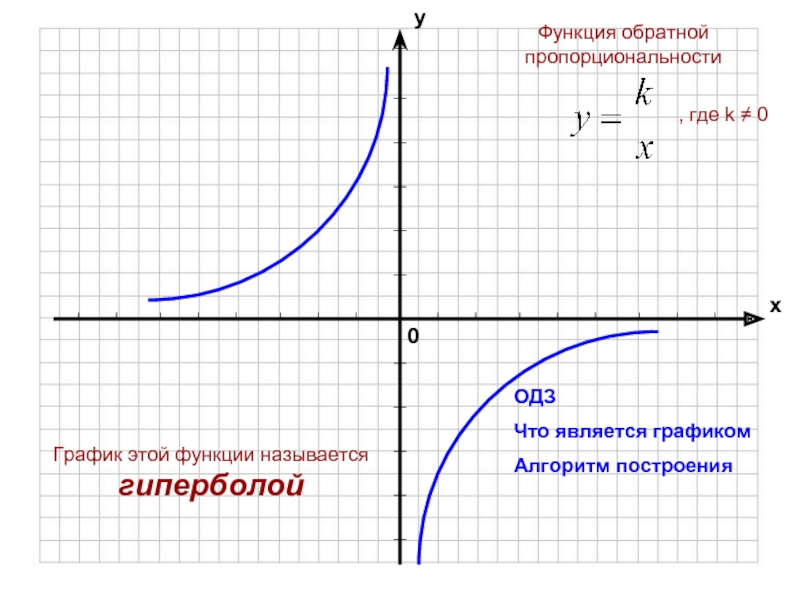
- 4. График этой функции называется гиперболойОДЗЧто является графикомАлгоритм построения
- 5. х2 + у2 = 25,
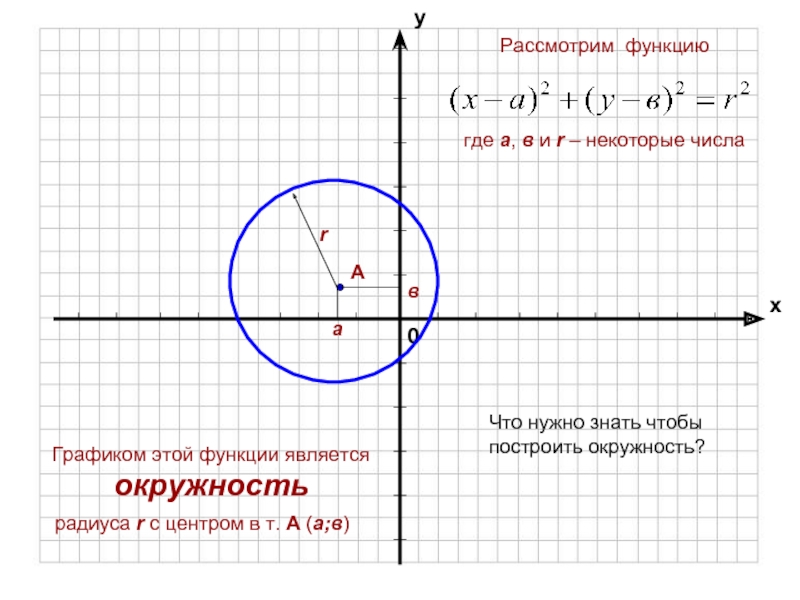
- 6. Что нужно знать чтобы построить окружность?
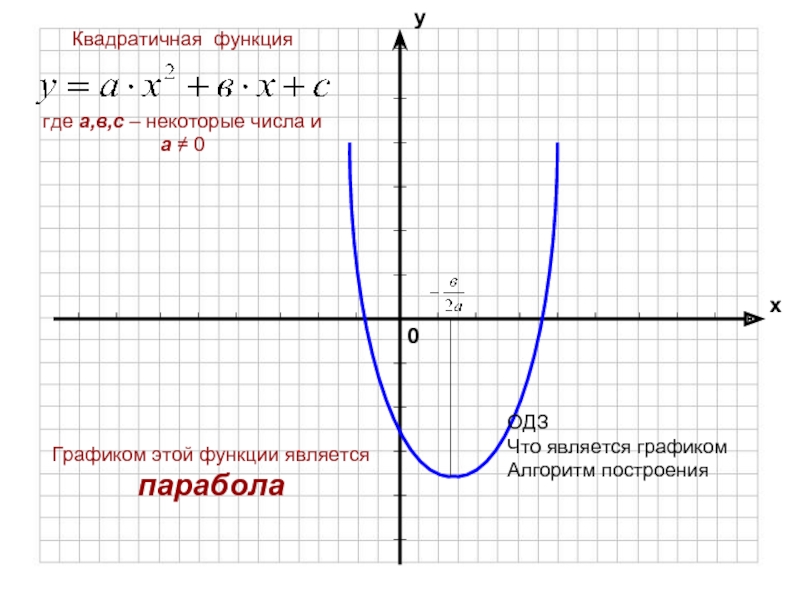
- 7. Графиком этой функции является параболаОДЗЧто является графикомАлгоритм построения
- 8. у = -х2 + 2х + 5; у = х2 + 2х + 5;
- 9. Алгоритм графического способа решения системы двух уравнений1234
- 10. Помните о двух вещах!Если точек пересечения графиков
- 11. Построим в одной системе координат графики уравненийх2
- 12. Скачать презентанцию
Слайды и текст этой презентации
Слайд 9Алгоритм графического способа решения системы двух уравнений
1
2
3
4
х2 +
у2 = 25у = -х2 + 2х + 5
Слайд 10Помните о двух вещах!
Если точек пересечения графиков нет, то система
решений не имеет;
Координаты точек пересечения определяются приблизительно, поэтому и решения
могут получиться приблизительными;Чтобы проверить точность полученных решений, их нужно подставить в уравнения системы!
Чтобы решить систему двух уравнений с двумя неизвестными, нужно:
Построить в одной системе координат графики уравнений, входящих в систему;
Определить координаты всех точек пересечений графиков (если они есть);
Координаты этих точек и будут решениями системы.
Дальше
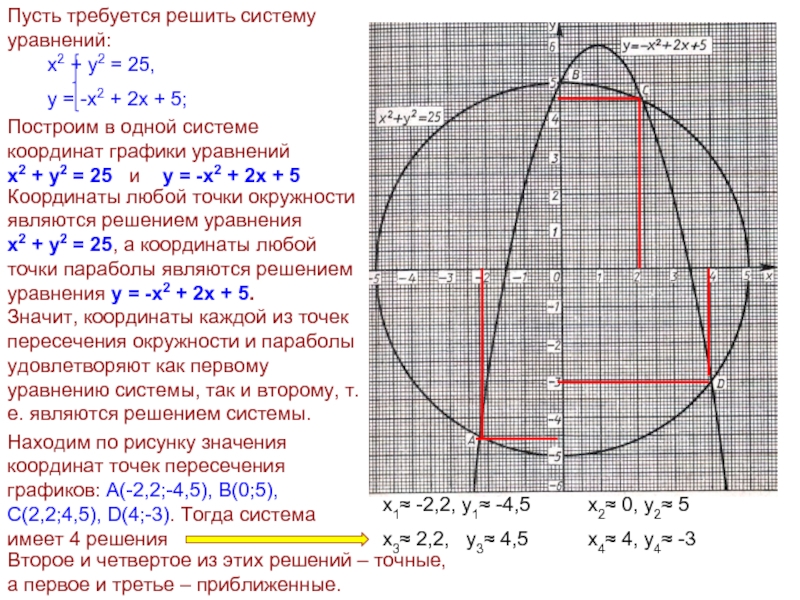
Слайд 11Построим в одной системе координат графики уравнений
х2 + у2 =
25 и у = -х2 + 2х +
5Координаты любой точки окружности являются решением уравнения х2 + у2 = 25, а координаты любой точки параболы являются решением уравнения у = -х2 + 2х + 5.
Значит, координаты каждой из точек пересечения окружности и параболы удовлетворяют как первому уравнению системы, так и второму, т.е. являются решением системы.
Находим по рисунку значения координат точек пересечения графиков: А(-2,2;-4,5), В(0;5),
С(2,2;4,5), D(4;-3). Тогда система имеет 4 решения
х1≈ -2,2, у1≈ -4,5 х2≈ 0, у2≈ 5
х3≈ 2,2, у3≈ 4,5 х4≈ 4, у4≈ -3
Второе и четвертое из этих решений – точные,
а первое и третье – приближенные.