Дефекты кристаллического строения

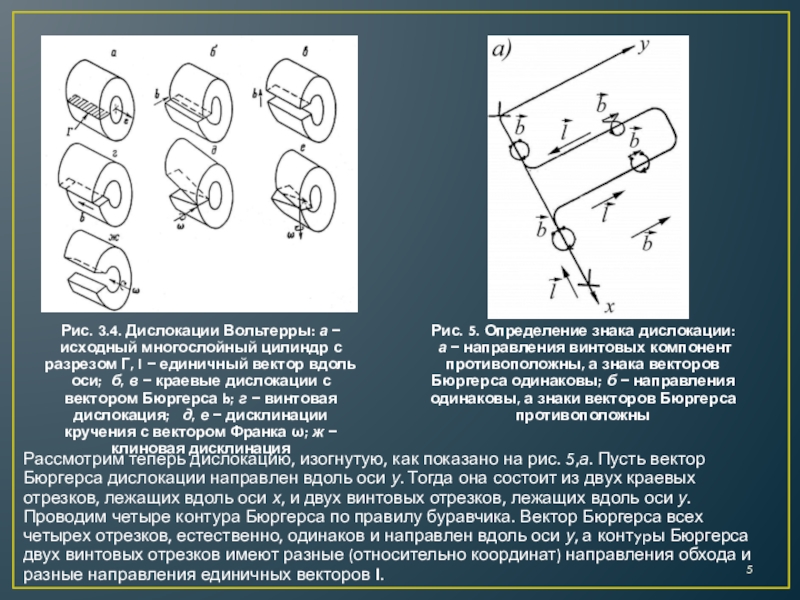
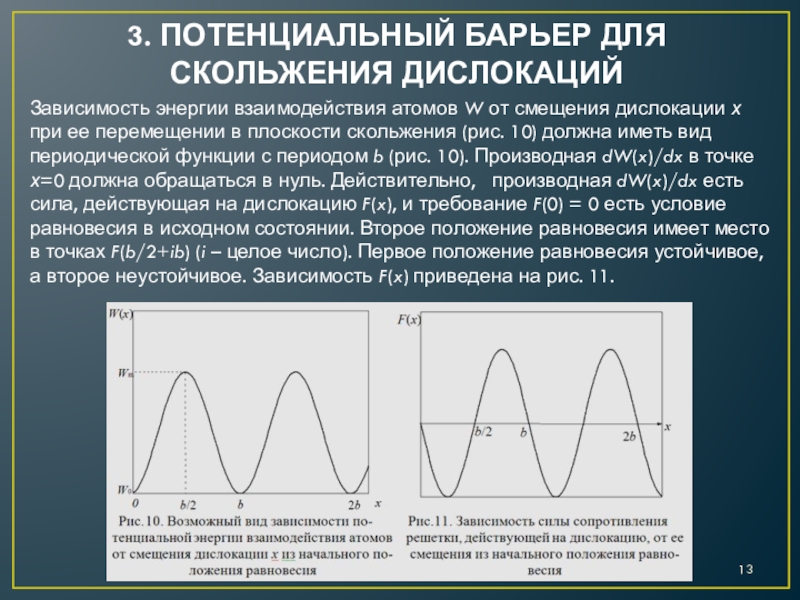
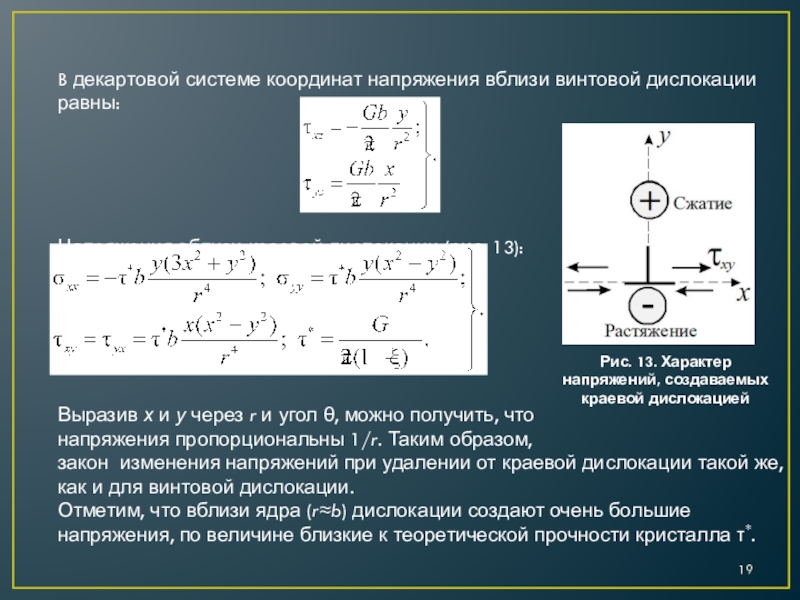
– l вектор, направленный вдоль оси дислокации:
а – общий

вид: б – атомное строение. Пунктиром обозначено сечение дислокационной трубки – области с нарушенным ближним порядком

Рассечем кристалл, со­держащий дислокацию, плоскостью BCDE, совпадающей с атомной плоскостью (рис. 1). В полученном сечении кристалла найдем окончание (край) лишней полуплоскости (экстраплоскости), вставленной в кристалл. Такое нарушение порядка чередования атомов в кристаллической решетке называют краевой дислокацией. Как видно по рисунку, область наибольших искажений решетки сосредоточена вблизи окончания экстраплоскости. Если область наибольших искажений очертить окружностью и проследить, как эта область искажений распространяется вглубь кристалла, то мы получим «дислокационную трубку». Сечение дислока­ционной трубки на плоскости BCDE будет выглядеть как окружность c радиусом порядка параметра кристаллической решетки а. Внутри этой окружности атомы имеют неправильное число ближайших соседей, а вне ее – правильное число, хотя рас­стояния между атомами и углы между ними несколько иска­жены из-за напряжений, вызываемых дислокацией.
Сравним участки двух плоскостей, одна из которых идеальная, а другую пересекает ось дислокации (рис. 2).

контур в идеальной решетке (б). Заштрихована область внутри дислокационной трубки

и соответствующая ей область в идеальной решетке

Выбор контура обхода. Обход кристалла с дислокацией. Обход идеального кристалла.
Контур и вектор Бюргерса. Величина b равна от­резку A1A, т. е. параметру решетки а, и он направ­лен вдоль оси х от A1 к А,

Некоторые важные положения о контуре Бюргерса:
1. Изменение направления обхода контура Бюргерса приводит к изменению направления вектора Бюргерса, определяющего знак дислокации. В связи с этим договорились обход контура всегда совершать по часовой стрелке.
2. Суммарная невязка контура равна сумме векторов Бюр­герса дислокаций, пересекающих ограниченную этим конту­ром поверхность.
3. Вдоль линии дислокации вектор Бюргерса не изменяется, поэтому можно сказать, что линия дислокации не может прерваться внутри идеального кристалла. Следовательно, дислокационные линии могут или выходить на поверхность кристалла, или образовывать замкнутые петли.
4. Вектор Бюргерса и ось дислокации, которая характеризуется ортом направления l связаны соотношениями, похожими на связь электрического тока с проводниками: ток не может течь по разомкнутому проводу, а только от положительного электрода источника тока к отрицательному по замкнутому проводу. Аналогично при разветвлении проводов суммарный ток через каждый узел сохраняется.

Если исключить из рассмотрения атомы, лежащие внутри дислокационной трубки, и соответствующие атомы в идеаль­ной решетке, то каждый атом в рассматри-ваемых плоскостях будет иметь по четыре ближайших соседа (в плоскости). Однако каждому атому идеальной решетки нельзя поставить в соответствие атом дефектной решетки.

ортом направления дислокации, направленным в каждой точке по каса­тельной к

ее оси, не постоянным по направ­лению, и сохраняющимся вектором Бюргерса b. Таким образом, плотность дислока­ции должна быть вели­чиной тензорной ρik (зна­чок i характеризует на­правление осей дислока­ции, k — направление век­торов Бюргерса).
5. Для определения единичного вектора l используют правило буравчика, где за направление вращения принято направление обхода по контуру Бюргерса, а за направление дислокации − поступательное движение буравчика.
6. По взаимной ориентации векторов l и b дислокации делятся на краевые (l  b), винтовые (l||b) и смешанные (=b,l , 0<<90° или 90°<<180°).
На предыдущих рисунках была изображена краевая
дислокация.

Рис. 3. Атомная структура вблизи линии винтовой дислокации СС

На рис. 3 показана атомная структура вблизи ядра винтовой дислокации. Видно, что кристалл, содержащий одну винтовую дислокацию, содержит всего одну плоскость, навитую, как спираль (или, лучше сказать, как гладкая винтовая лестница), на ось винтовой дислокации.
Поскольку вопрос о характере искажений, вносимых в кристалл дислокациями, возникает достаточно часто, представим их в виде схемы, представленной на рис. 4.

разрезом Г, l  единичный вектор вдоль оси; б, в

 краевые дислокации с вектором Бюргерса b; г  винтовая дислокация; д, е  дисклинации кручения с вектором Франка ; ж  клиновая дисклинация

Рис. 5. Определение знака дислокации:
а  направления винтовых компонент противоположны, а знака векторов Бюргерса одинаковы; б  направления одинаковы, а знаки векторов Бюргерса противоположны

Рассмотрим теперь дислокацию, изогнутую, как показано на рис. 5,а. Пусть вектор Бюргерса дислокации направлен вдоль оси у. Тогда она состоит из двух краевых отрезков, лежащих вдоль оси х, и двух винтовых отрезков, лежащих вдоль оси у. Проводим четыре контура Бюргерса по правилу буравчика. Вектор Бюргерса всех четырех отрезков, естественно, одинаков и направлен вдоль оси у, а контypы Бюргерса двух винтовых отрезков имеют разные (отно­сительно координат) направления обхода и разные направления единичных векторов l.

противоположны
Представим теперь, что наше поле зрения ограничено, и мы видим

только небольшие части винтовых отрезков (рис.5,б). Естественно предположить, что направления обхода контура Бюргерса мы примем по часовой стрелке для каждого из отрезков. В этом случае направления ортов l будут параллельны и одинаково направлены. Однако по сравнению с рис. 3.5,а для верхнего винтового отрезка мы изменили направление обхода контура Бюргерса на противоположный. Поэтому и направление вектора Бюргерса для верхнего отрезка изменится на противоположный по сравнению с рис. 5,а. Таким образом, для одного и того же отрезка дислокации при смене направления орта l автоматически изменяется направление вектора Бюргерса.

Отсюда следует важный вывод, что дислокации противоположного знака имеют или противоположные векторы Бюргерса, или противоположные направления. Дислокации же с противоположными и векторами Бюргерса, и направлениями, имеют один знак, так как, поменяв направление какой-либо из них, мы меняем одновременно и вектор Бюргерса.

движение дислокаций: а – исходный образец; б – сдвинутый по

плоскости АА на постоянную решетки; в – образование краевой дислокации с вектором Бюргерса b=a на плоскости АА; г – движение дислокации по плоскости АА

Возьмем кубический образец (рис. 6,а) и сдвинем его верхнюю половину по плоскости АА на расстояние, равное параметру кристаллической решетки а (рис. 6,б). При этом длина образца увеличивается L' = L + ΔL; ΔL ≈ a. Из состояния, показанного на рис. 6,а, в состояние рис.6,б можно перейти двумя способами:
- сдвинув одновременно всю верхнюю часть кристалла относительно нижней (для этого надо приложить скалывающее напряжение, равное теоретической прочности, см. лекцию 1;
- образовав на плоскости АА краевую дислокацию с век­тором Бюргерса b=а и продвинув ее с левого края кристалла на правый (рис. 6, в и г).
И в том и в другом случае удлинение кристалла одина­ково: L1≈ L+a. Постепенное перемещение дислока­ции с вектором Бюргерса b по какой-либо плоскости эквивалентно одновременному сдвигу одной части кристалла относительно другой на b вдоль плоскости скольжения дислокации.
Пластическая деформация при таком перемещении одной дислокации
(1)

б) в)

Рис. 7. Перемещение дислокации в плоскости скольжения

векторы b и l. Плоскость, проведенная через ось дислокации и

вектор Бюргерса, называется поэтому плоскостью скольжения. Этим термином мы уже пользовались несколько раз, не расшифровывая его смысл.
2. Общее число разорванных связей (для простого кубического кристалла в нашем приближении две связи 5‒7 и 5‒8, рис. 7,а) после смещения дислокации на целое число шагов сохраняется. В рассмотренном выше примере после одного скачка остались две разорванные связи 6‒8 и 6‒9 (рис. 7,в). Именно сохранение общего числа разорванных связей и делает такое движение дислокации обратимым.
3. Краевые дислокации имеют одну плоскость скольжения: через две пересекающиеся прямые (ось дислока­ции и вектор Бюргерса) можно провести одну и только одну плоскость. Винтовая дислокация имеет столько плоскостей скольжения, сколько через нее можно провести кристаллографических плоскостей, т. е. число плоскостей скольжения зави­сит от ее ориентации и от типа кристаллической решетки. Реально винтовая дислокация может перемещаться по (2÷4) плоскостям скольжения.
4. Движение дислокации в плоскости скольжения напоминает эстафетное движение, в котором каждый из бегунов про­бегает малую часть всей дистанции, а весь путь проходит только эстафетная палочка.
Всякое движение дислокации под углом к плоскости скольжения называется неконсервативным или переползанием. Процесс переползания связан с диффузией больших групп вакансий или внедренных атомов, поэтому переползание  относительно медленный процесс, сильно зависящий от температуры.
5. Из-за низкой скорости переползания ее непосредственный вклад в скорость деформации мал:


где vпер – средняя скорость переползания дислокации.

Рассмотрим его.
Рис. 8. Движение винтовой дислокации со ступеньками:

а – истинная конфигурация; б – эффективная конфигурация

Пусть в простой кубической решетке есть дислокация с ломаной линией, состоящая из длинных lв>>а отрезков винтовой ориентации и коротких lк~a отрезков краевой дислокации. Движение в направлении х требует переползания краевых отрезков. Но поскольку перемещение всех их на расстояние а приводит к такому же перемещению всей дислокации, то эффективная скорость дислокации увеличивается в lв/lк раз. Действительно, если поглощение n вакансий в секунду на 1 м длины чисто краевой дислокации приводит к ее скорости

плоскости скольжения. Это происходит при температурах деформации, при которых диффузия

вакансий происходит достаточно эффективно. Пусть крае­вая дислокация встречает расположенные равномерно препятствия А размером r и рас­стоянием между ними l в плоскости ее скольжения (рис. 9). Повторяя предыдущие рассуждения, получим, что скорость дислокации

Так как r обычно порядка нескольких а, то vэфф>>vк пер. Переползание играет при этом механизме вспомогательную роль, освобождая дислокацию от препятствий, а основной вклад (как и в случае движения винтовой дислокации со ступеньками) в пластическую деформацию вносит скольжение.

Рис. 9. Движение дислокации gg в плоскости скольжения П, содержащей препятствия А, путем их переползания:
а – исходное положение; б – переползание отрезков дислокации вблизи препятствий, обеспечивающее их свободное движение

Таким образом, существуют два типа движения дислокации: быстрый – скольжение и медленный – переползание, причем переползание играет существенную роль обычно только тогда, когда скольжение дислокации по каким-либо причинам затруднено.

от смещения дислокации х при ее перемещении в плоскости скольжения

(рис. 10) должна иметь вид периодической функции с периодом b (рис. 10). Производная dW(x)/dx в точке х=0 должна обращаться в нуль. Действительно, производная dW(x)/dx есть сила, действующая на дислокацию F(x), и требование F(0) = 0 есть условие равновесия в исходном состоянии. Второе положение равновесия имеет место в точках F(b/2+ib) (i – целое число). Первое положение равновесия устойчивое, а второе не­устойчивое. Зависимость F(x) приведена на рис. 11.

порядку величины (см. рис. 10 и 11) равна

(9)

Более точные расчеты были проведены Френкелем и Канторовой, Пайерлсом, Набарро и др. Наиболее известна модель Пайерлса. Тело разбивается на два полупространства плоскостью скольжения (плоскость АА, см рис. 7). Считается, что к каждому из полупространств применима линейная теория упругости и что атомы, лежащие в плоскости скольжения, взаимодействуют с атомами противолежащего полупространства по периодическому закону, подобно изображенному на рис. 11. В качестве простейшего приближения был принят синусоидальный закон вида

(10)

отличающийся от (9) только введением двух постоянных решетки а и b вместо одной а.
В этих приближениях величина WП = W – W0 оказалась равной:

(11)

Рис. 7,а - повтор

W(x), равно (σк ~ Fmax /b)

(12)

где, как и ранее, k = l для винтовой и k = 1 – v для краевой дислокации. Напряжение τП часто называют напряжением Пайерлса.
Замечания к формулам (11) и (12):
1. Поскольку при выводе формул делались очень грубые предположения, они могут быть справедливы только качественно, количественные оценки могут совпадать с экспериментом только по порядку величины.
2. Напряжение τП гораздо меньше теоретического напряжения для сдвига в идеальной решетке τ0 ≈ G/6 [см. лекцию 1]. Так, для простой кубической решетки a=b, ξ = l/3 и k =2/3 (краевая дислокация), τп = 2,5ּ10 –4 G<<0.
3. В (10) не учтены типы межатомных связей и типы кристаллических решеток. Величины WП и τП для некоторых материалов с различными типами связей в решетке для плоскостей с максимальными значениями а/b даны в табл. 1.
4. Наиболее важный качественный вывод из формулы (11): τП тем меньше, чем меньше вектор Бюргерса дислокации b, и тем больше, чем меньше расстояние а между плоскостями в нормальном к плоскости скольжения направлении. Даже при небольшом уменьшении a/b напряжение τП меняется очень сильно. Например, для при a/b=1 τП ≈ 2,510–4 G и при а/b=1,5 τП≈610 –3 G, т. е. увеличивается примерно в 20÷25 раз.

лежащие в плоскостях, расстояние а между которыми велико. Легко сообразить,

что двум этим требованиям, например, в ГЦК решетке удовлетворяют плотноупакованные плоскости типа {111}. Будем их называть плоскостями легкого скольжения. Для ОЦК решетки – это плоскости {110}, для ГПУ –
(0001).
Т а б л и ц а 3.1
Значения потенциального барьера для перемещения дислокаций
по кристаллической решетке некоторых металлов







5. Дислокация обладает высокой подвижностью, если ее плоскость скольжения (плоскость, проведенная через ось дислокации и вектор Бюргерса) совпадает с какой-либо плоскостью легкого скольжения, а ее вектор Бюргерса минимальный из всех возможных. Наоборот, если плоскость скольжения дислокации такова, что для нее отношение а/b очень мало, то τП для нее велико и дислокация является практически неподвижной или, как часто говорят, сидячей.

подвижны, чем винтовые. Действительно, со­гласно условиям, сформулированным в п. 2,

при а/b=1 для краевых дислокации τкП ≈ 2,5ּ10–4 G, а для винтовых τвП≈4ּ10–3 G. Это обстоятельство должно быть наиболее суще­ственно для кристаллов с высоким барьером Пайерлса WП.
Итак, мы получили очень важные качественные результаты, такие, как наличие плоскостей легкого скольжения, зависимость напря­жения Пайерлса τП от величины вектора Бюргерса, типа дислокации, характера связей между атомами и типа кри­сталлической решетки.

5. Напряжения от дислокации

Рис. 12. Смещения и деформации около винтовой дислокации

Рассмотрим напряжения от винтовой дислокации, рис.12. Пусть ось винтовой дислокации направлена вдоль оси z. Выберем какую-либо точку 1, расположенную на расстоянии r от оси, и опустим из нее на ось перпендикуляр, приняв точку пересечения за начало координат 0. Построим контур Бюргерса, начинающийся в точке 1. Тогда его конечная точка 2 будет лежать в плоскости 10z (проходящей через ось z и точку 1) и отстоять от точки 1 на вектор Бюргерса дислокации b.

перпендикулярен 0z, конечный 02 после поворота на 2π наклонен под

углом
к 01 и углом к оси. Так как все радиус-векторы у винтовой дислока-
ции равноправны, то наклон ω должен меняться плавно от 0 до b/r при изменении
θ от 0 до 2π, т. е.
Относительная деформация решетки ε характе­ризуется скоростью изменения смещения координаты i при изменении координаты k. Из предыдущего рассуждения видно, что в слу­чае винтовой дислокации имеются только смещения в направлении z, меняющиеся при изменении θ, т.е.


От деформации перейдем к напряжению: τzθ =Gεzθ, где G – модуль сдвига. Отсюда

(13)
Из условия равновесия θz = zθ. В силу симметрии по углу θ напряжения зависят только от модуля r. Основной характеристикой внутренних напряжений является закон их уменьшения при удалении от источника. Из (13) видно, что θz = zθ 1/r. Таким образом, дислокации являются источниками дальнодействующих внутренних напряжений.

краевой дислокации (рис. 13):






Выразив х и у через r

и угол θ, можно получить, что
напряжения пропорциональны 1/r. Таким образом,
закон изменения напряжений при удалении от краевой дислокации такой же, как и для винтовой дислокации.
Отметим, что вблизи ядра (rb) дислокации создают очень большие напряжения, по величине близкие к теоретической прочности кристалла *.

Рис. 13. Характер напряжений, создаваемых краевой дислокацией