Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ДИСПЕРСИЯ И ЕЕ СВОЙСТВА Дисперсия - это мера рассеяния значений случайной
Содержание
- 1. ДИСПЕРСИЯ И ЕЕ СВОЙСТВА Дисперсия - это мера рассеяния значений случайной
- 2. Для вычисления дисперсии обычно используют другую формулу:
- 3. Доказательство:Используем свойства математического ожидания:
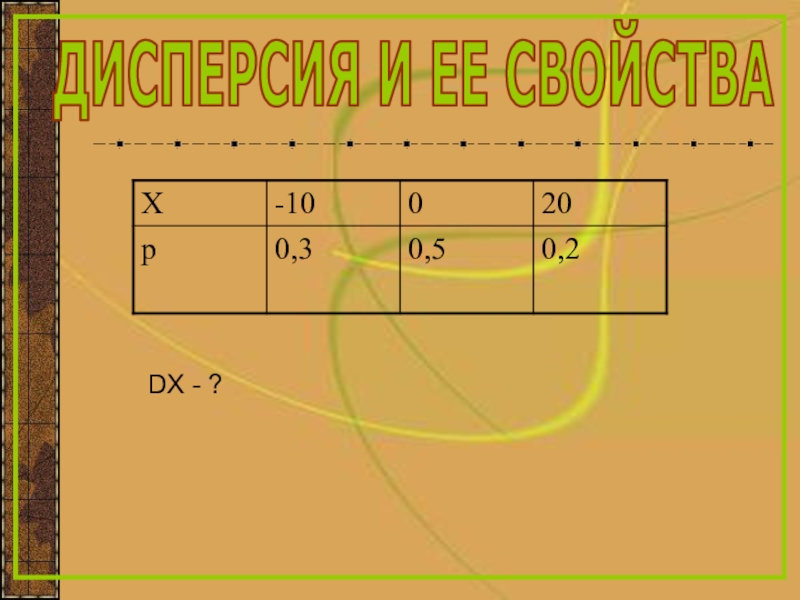
- 4. ДИСПЕРСИЯ И ЕЕ СВОЙСТВАDX - ?
- 5. ДИСПЕРСИЯ И ЕЕ СВОЙСТВА
- 6. Квадратный корень из дисперсии называется средним квадратичным
- 7. ДИСПЕРСИЯ И ЕЕ СВОЙСТВАВ среднем значения случайной величины отличаются от среднего 1 На 10.44
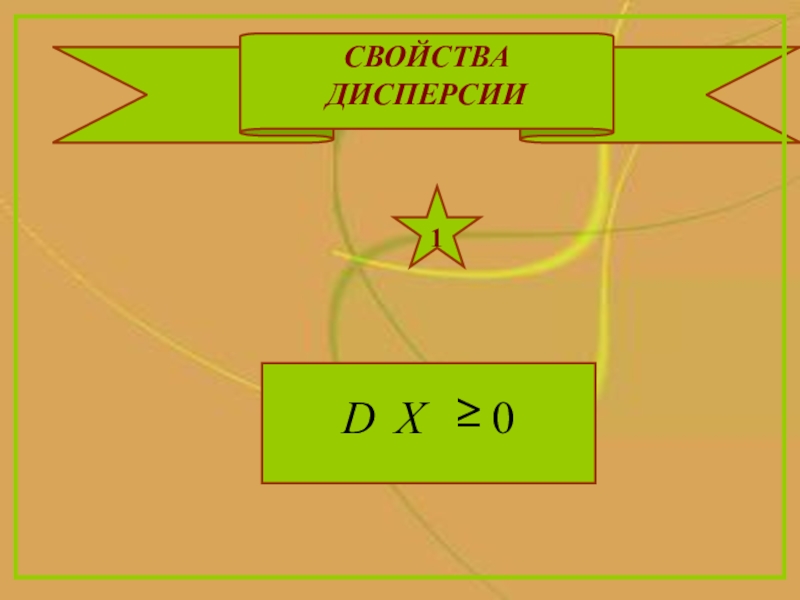
- 8. СВОЙСТВА ДИСПЕРСИИ1
- 9. 2Дисперсия от постоянной величины равна нулю: DC=0, C=const
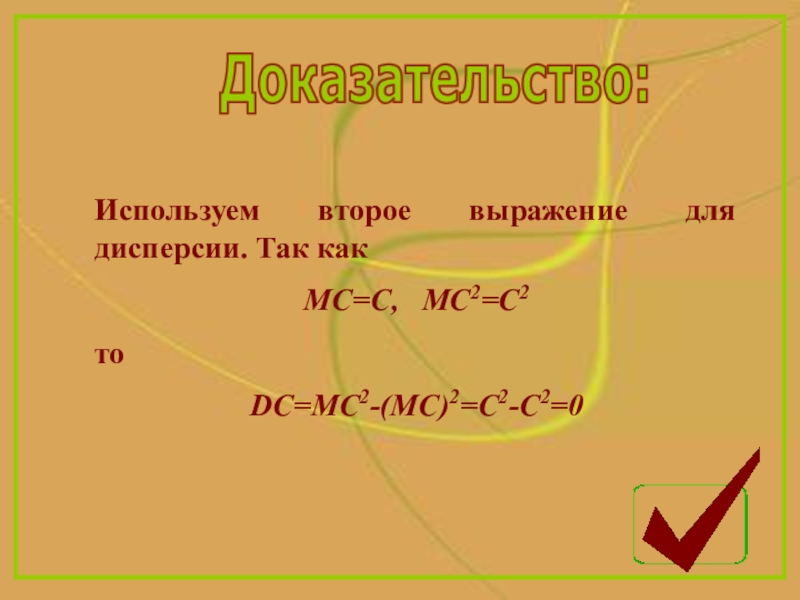
- 10. Доказательство:Используем второе выражение для дисперсии. Так как MC=C, MC2=C2тоDC=MC2-(MC)2=C2-C2=0
- 11. Постоянная величина выносится за знак дисперсии в квадрате: D(С X)=С2 DX3
- 12. Доказательство:По свойству математического ожидания:Используем определение дисперсии:
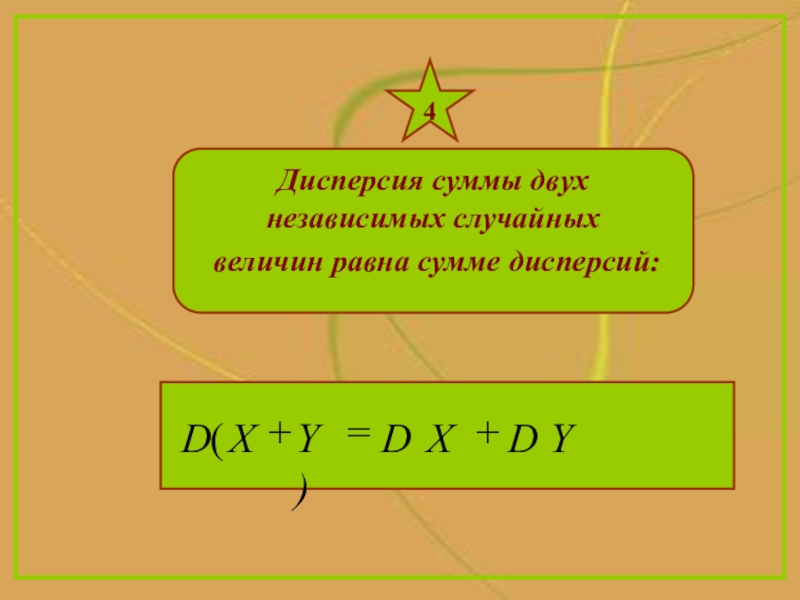
- 13. 4Дисперсия суммы двух независимых случайных величин равна сумме дисперсий:
- 14. Распишем дисперсию суммы случайных величин по определению дисперсии:Доказательство:
- 15. Пример: В страховой компании застраховано 10 тысяч
- 16. Пример: В страховой компании застраховано 10 тысяч
- 17. Пример. В страховой компании застраховано 10 тысяч
- 18. Пример. В страховой компании застраховано 10 тысяч
- 19. Пример. В страховой компании застраховано 10 тысяч
- 20. Пример: Стоимость акции некоторой компании в настоящий
- 21. Пример: Инвестор может приобрести акции двух компаний.
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 6Квадратный корень из дисперсии называется средним квадратичным отклонением:
СКО показывает среднее
отклонение случайной величины от своего среднего значения.
Слайд 7ДИСПЕРСИЯ И ЕЕ СВОЙСТВА
В среднем значения случайной величины отличаются от
среднего 1
На 10.44
Слайд 10Доказательство:
Используем второе выражение для дисперсии. Так как
MC=C, MC2=C2
то
DC=MC2-(MC)2=C2-C2=0
Слайд 15Пример: В страховой компании застраховано 10 тысяч человек. Каждый застрахованный
выплачивает в год 1 тыс. рублей. Вероятность наступления страхового случая
в течение года для одного застрахованного 0,01. Выплата при наступлении страхового случая равна 50 тыс. рублей. Пусть X – прибыль страховой компании за год. Найти MX, DX,Слайд 16Пример: В страховой компании застраховано 10 тысяч человек. Каждый застрахованный
выплачивает в год 1 тыс. рублей. Вероятность наступления страхового случая
в течение года для одного застрахованного 0,01. Выплата при наступлении страхового случая равна 50 тыс. рублей. Пусть X – прибыль страховой компании за год. Найти MX, DX,- прибыль от i-го застрахованного, i=1,2…10000
Слайд 17Пример. В страховой компании застраховано 10 тысяч человек. Каждый застрахованный
выплачивает в год 1 тыс. рублей. Вероятность наступления страхового случая
в течение года для одного застрахованного 0,01. Выплата при наступлении страхового случая равна 50 тыс. рублей. Пусть X – прибыль страховой компании за год. Найти DX.- прибыль от i-го застрахованного, i=1,2…10000
Слайд 18Пример. В страховой компании застраховано 10 тысяч человек. Каждый застрахованный
выплачивает в год 1 тыс. рублей. Вероятность наступления страхового случая
в течение года для одного застрахованного 0,01. Выплата при наступлении страхового случая равна 50 тыс. рублей. Пусть X – прибыль страховой компании за год. Найти DX.- прибыль от i-го застрахованного, i=1,2…10000
Средняя прибыль компании составит 5 млн. руб. Среднее отклонение от этого
Значения равно 497 494 рубля (около 500 тысяч рублей).
Слайд 19Пример. В страховой компании застраховано 10 тысяч человек. Каждый застрахованный
выплачивает в год 1 тыс. рублей. Вероятность наступления страхового случая
в течение года для одного застрахованного 0,01. Выплата при наступлении страхового случая равна 50 тыс. рублей. Пусть X – прибыль страховой компании за год. Найти DX.Слайд 20Пример: Стоимость акции некоторой компании в настоящий момент составляет 100
д.е. В следующем месяце стоимость может возрасти на 10 д.е.
с вероятностью 0,7, остаться неизменной с вероятностью 0,2 и упасть на 10 д.е. с вероятностью 0,1. Пусть X – стоимость акции через месяц. Найти MX, DX,Слайд 21Пример: Инвестор может приобрести акции двух компаний. Начальная стоимость акций
одинакова и составляет 100 д.е. В следующем месяце
Для 1-й компании
рост на 10 д.е. с вероятностью 0,7,
без изменений с вероятностью 0,2
падение на 10 д.е. с вероятностью 0,1
Для 2-й компании
рост на 20 д.е. с вероятностью 0,6,
без изменений с вероятностью 0,1
падение на 20 д.е. с вероятностью 0,3
Акции какой компании лучше купить инвестору?