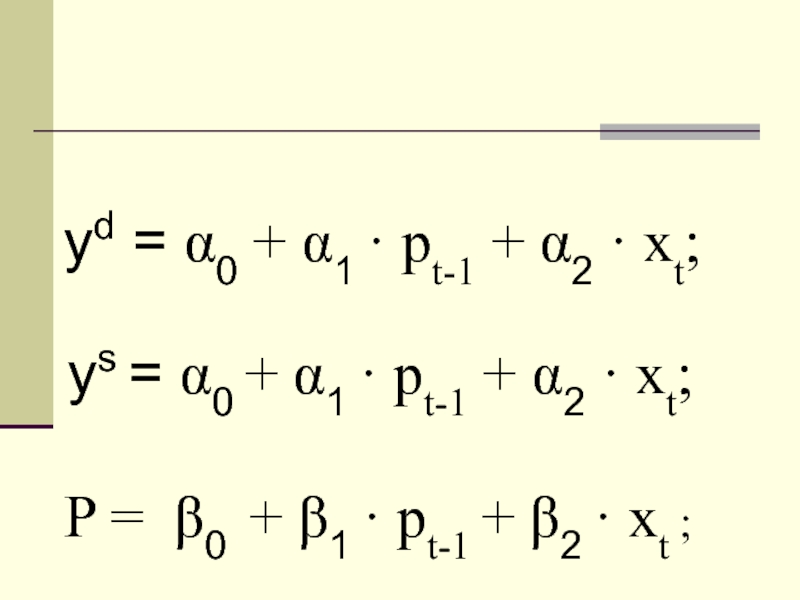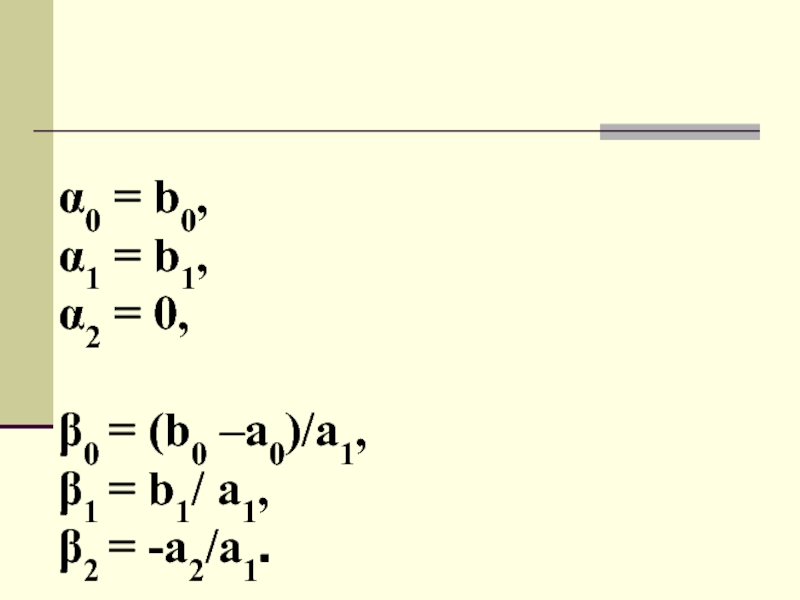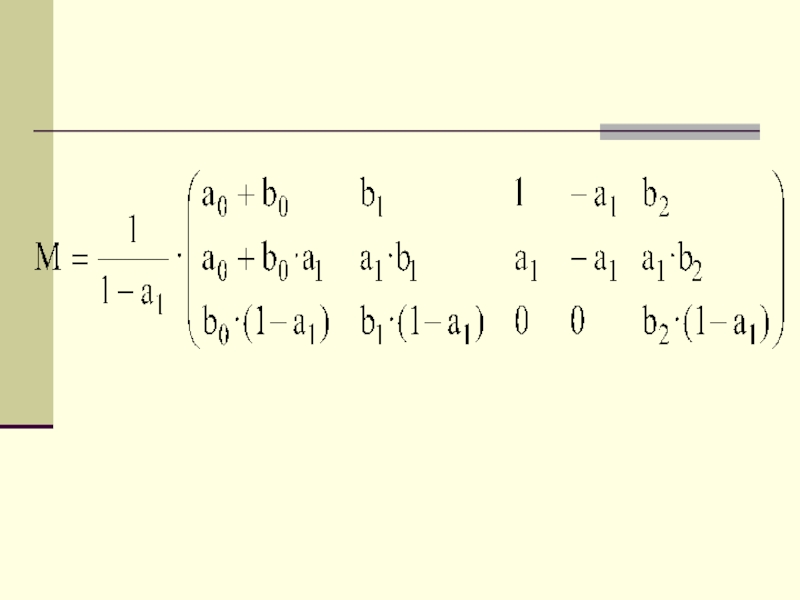Дисциплина ЭКОНОМЕТРИКА

технологий 
Финансовый университет при Правительстве Российской Федерации
Nevezhin@fa.ru

– разбор общего примера соответствующего кейса и его самостоятельное выполнение

(дома)
– ответы на вопросы и разбор решения общего примера, приведенного в кейсе
3. Самостоятельная работа по ДТР со своим выбранным индивидуальным заданием («дома») – 50%

– до 25 октября 2019 – 20 баллов

Часть 2 ДТР

- до 18 декабря 2019 – 50 баллов

Наличие публикации (статьи по тематике курса) в рамках данной дисциплины – бонусы к экзамену, при условии соблюдения других правил
Кто не сдал ДТР в указанные сроки: (-) 5 баллов к экзамену за каждую работу (ДТР) .

35
Самостоятельная работа (ДТР 1 ч.) - 20
Промежуточный тест по теории - 30
______________________________________
Итого

100
переводится в 20 баллов промежуточной аттестации

35
Самостоятельная работа (ДТР 1 ч.) - 50
_____________________________________
Итого 100
переводится в

20 баллов в конечную аттестацию

за II часть семестра - 20 **
Итого

- 40
Экзамен - 60
Экзаменационная задача - 30
(тест по всему объему предмета) - 30 **
или
2 вопроса экзамена - 15х2=30
____________________________________
Всего - 100

и лекциям
2 Дома выполняется общая задача соответствующего кейса
3 На семинарском

занятии задаются вопросы по пройденному дома материалу и выполняется практическая работа
4 Самостоятельно выполняются соответствующие части ДТР и вносятся полученные результаты в отчет (по форме)

Для работы с материалом ДТР рекомендуется приобрести отдельную папку (формат А4) для подшивки в нее результатов

В.П. Невежин, Ю.В. Невежин. – М.:  ИНФРА-М;  ИД  Форум,  2016.+

 Доп.  материалы  [Электронный  ресурс;  URL:  http://www.znanium.com].  —  (Высшее образование: Бакалавриат). — www.dx.doi.org / 10.12737 .
2. Бабешко, Л.О. Основы эконометрического моделирования: учеб. пособие. Изд. 2-е. испр. / Л.О. Бабешко. – М.: КомКнига, 2006, -432 с.
3. Бывшев, В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. -480 с.
4. Доугерти, К. Введение в эконометрику: учебник : пер. с англ./ К. Доугерти. – М.: Инфра-М, 2009.
5. Елисеева, И.И. Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордиенко и др., под ред. И.И. Елисеевой. – М.: Финансы и статистика. 2001.
6. Эконометрика: учебник для магистров / И.И. Елисеева [и др.]; под ред. И.И. Елисеевой. – М.: Изд-во «Юрайт», 2012. – 453 с.

Рекомендуемая литература

– среднее квадратичное отклонение
a0, а1 – исходные значения эконометрической модели
â0

, â1 , ŷ – оцененные значения параметров регрессии
ӯ – среднее арифметическое значение (мат ожидание)
Сov – ковариация
ρху , rx,y– коэффициент корреляции между х и у

для определенных целей.
Модель = образец.
Модель − знаковый объект-заместитель, который в

определенных условиях может заменять объект оригинал. Принцип подобия.
СубъекТ

Объект МОДЕЛЬ
Соц. среда

управления ими.
Создание вариантов при проектировании с возможностью их оценки. Естественный

отбор при проектировании.
Различные модели предназначены для различных целей.
Модель «Тасýнок» – нет модели в голове, нет понимания.
Парадокс: Дневники заполняют с 1 класса, но практически никто не ведет дневники и не планирует свою деятельность. Модели есть всюду, но никто не может, к сожалению, верно выполнять моделирование.

Кодирование информации для ее передачи другим людям. Понимание – соотнесение

знаков с реальностью, восстановление образа явления при декодировании знакового сообщения. То есть создание образной модели.

Знаки − объекты-заместители, которым поставлены в соответствие другие объекты и явления реальности. Они отображают не сам объект, а информацию о нем.

символы, иероглифы);

Логические (семиотические, лингвистические, математические) − от logos − слово;

кодирование (от codex – книга) информации с помощью абстрактной системы знаков (языка).

Цифровые (компьютерные).

реальностью.
Ограниченность (конечность) возможностей человека  Конечность моделей  их упрощенность

и приближенность  вопросы адекватности моделей.
Абстракция – упрощение реальности. Упрощенность модели позволяет оперировать с ней человеку.
Научные упрощения (абстракции): вещественное число, точка, однородность, непрерывность, вакуум, ток, гравитация.
Абстракция линейности – важнейшая математическая абстракция. Линейность в малом – дифференциальное исчисление.
 

что отбрасывать? Учет всего, что имеет прямое отношение к целевой

задаче.
Адекватность моделей реальности – модель рассматривается, как возможность достижения поставленной цели с приемлемой «точностью».
Любая модель – это компромисс:
Полнота – простота; Точность – размерность;
Эффективность – затраты на реализацию и расчеты.
 Динамика моделей:
Историчность развития – как основа понимания. Усложнение модели в развитии. Обращение к первоисточникам для понимания сути.

количественные закономерности и взаимосвязи между переменными экономических объектов с помощью

математических методов и моделей».

Р. Фриш подчеркивает, что эконометрика есть единство трех составляющих:
- математической статистики,
- макроэкономики,
- микроэкономики.

количественными характеристиками экономических объектов в целях построения математических правил прогноза

(вычисления приближённых значений) недоступных для наблюдения количественных характеристик объектов по наблюдённым или заданным значениям других количественных характеристик объектов.
Эмпирическим материалом для построения правил прогноза (эти правила именуются эконометрическими моделями) служат результаты наблюдений за изучаемыми экономическими объектами.

– наполнить эмпирическим содержанием априорные экономические рассуждения», т.е. ставится задача

придать количественные оценки выводам и закономерностям, сформулированным в общей экономической теории.

Как известно, в большинстве случаев основные результаты общей экономической теории носят качественный характер, а эконометрика переводит их на количественный уровень.

прогнозирования поведения экономического объекта в различных ситуациях и на ее

базе решать практические задачи по управлению объектом, выбору стратегии поведения на рынке и т.п.
Задача - определить значения всех числовых параметров, входящих в модель и обеспечить соответствие ее (модели) реальному поведению объекта.
Исходной информацией для решения поставленной задачи являются результаты наблюдения за объектом и качественные выводы общей экономической теории.

– (1).
(выбираются переменные (факторы), их типы, структура и математическая запись

модели)
- Сбор и первичная обработка исходной информации (использование статистики) – (2).
- Оценивание параметров модели и их статистической значимости – (3).
- Проверка качества и адекватности модели – (4).
(выполняется верификация модели - проверка насколько хорошо построенная модель описывает экономические реалии).
- Практическое использование модели - (5).

это любая хозяйствующая единица.

Переменная – количественная характеристика объекта, которая может

принимать различные значения в процессе хозяйственной деятельности объекта.

Модель – набор графиков или таблиц, либо система математических уравнений и неравенств, связывающих воедино все переменные объекта.

Переменные: – относительная цена автомобиля «Р», – возраст

автомобиля «а»,
– пробег «d».
Модель: P = f(a,d).

Пример 2. Объект – конкурентный рынок.
Переменные – спрос “Yd”, предложение “Ys”, установившаяся цена “P”.
Модель: Yd=f(p), Ys=φ(p), Yd= Ys.

формируется внутри модели в результате взаимодействия с другими переменными.

Определение. Экзогенной

(независимой) переменной называется переменная, значение которой формируется вне модели.

дело с линейной эконометрической моделью, например, моделью вида:
Y= α0 +

α1X1 + α2X2 + ... + akXk+ ε.
в котором Y – объясняемая переменная, а X1, X2, … ,Xk - объясняющие переменные
Символом ε (u) обозначаются так называемые случайные отклонения эконометрической модели.

которых должны оцениваться. Они называются параметрами модели.
Параметры бывают двух

видов.
Первый вид — структурные параметры, от которых зависит значение функции объясняющих переменных. Это α1, α2, … αk.
Второй вид — параметры стохастической структуры модели. Эти параметры определяют распределение случайных отклонений параметров модели, таких как математическое ожидание и дисперсия случайных отклонений, а также их коэффициентов автокорреляции.

класса:

- причинно-следственные модели,
- симптоматические модели,
- авторегрессионные модели
- модели тенденции развития.

и объясняющими переменными существует причинно-следственная зависимость. Объясняемая переменная модели -

играет роль следствия, а объясняющие — причины.
В авторегрессионных моделях роль объясняемых переменных играют сдвинутые по времени объясняемые переменные. Такие модели применяются, в основном, для исследования явлений с инерционностью.
Модели тенденции развития описывают развитие явлений во времени. В них объясняемые переменные представляются функциями единственной переменной времени t, которая чаще всего принимает значения из натурального ряда чисел

формирование одной переменной (парная регрессия)
- многомерные - описывающие одновременное формирование

нескольких переменных (множественная регрессия)

По аналитической форме
Разделяют на линейные и нелинейные.
В линейной модели - объясняемая переменная является линейной функцией объясняющих линейных переменных и случайного отклонения.
Среди нелинейных моделей можно выделить модели, нелинейные относительно объясняющих переменных, но линейные относительно структурных параметров, а также модели, нелинейные относительно и объясняющих переменных, и структурных параметров.

языке.
Принципы спецификации модели
Первый. Экономические закономерности поведения объекта (экономическая задача), переводятся

на математический язык. Записываются уравнения, желательно линейные.
Пример (из эконом. теории). Конкурентный рынок товара. Задача – получить модель, связывающую между собой уровни спроса Yd и предложения Ys и равновесной цены р.
Из экономической теории известно:
1. Спрос на товар тем выше, чем ниже его цена.
2. Предложение товара растет с ростом цены.
3. Равновесная цена соответствует равенству между спросом и предложением.

записать утверждения (1-3) на математическом языке. В рамках линейных алгебраических

функций модель примет вид:
Yd = a0 + a1*p
Ys = b0 + b1*p (1.1)
Ys = Yd
a0>0, b0>0, b1>0, a1<0
В модели (1.1) Yd , Ys , р – переменные объекта, a0 , a1, b0, b1 – неизвестные параметры.
Модель состоит из переменных объекта (модели), называемых часто факторами, и ее параметров.

Переменные модели могут принимать различные значения, соответствующие состоянию рынка, а параметры являются константами, назначение которых обеспечить адекватность модели реальному объекту.

= X (1.2)
Х и Y векторы переменных модели, а А -

матрица параметров модели.

Модель Кобба - Дугласа (производственная функция)
Y = a0•Kα•L(1-α) (1.3)
(Y, K, L) - переменные модели, a0,α - параметры модели
Замечание. Модели (1.1) и (1.2) представляют собой систему линейных алгебраических уравнений, а модель (1.3) состоит из одного (изолированного) уравнения.

доход потребителя. Из теории известно, что спрос на товар растет

с ростом дохода потребителя. Тогда спецификацию модели (1.1) можно записать в виде:
Yd = a0 + a1•p +a2•x
Ys = b0 + b1•p (1.4)
Ys = Yd
(a0 , a2, b0 , b1)>0
a1<0
Замечание. В модели (1.4) значение переменной х формируется вне зависимости от состояния конкурентного рынка, т.е. х является независимой переменной, значение которой влияет на состояние рынка как внешний фактор.

Независимыми переменными являются также конечный спрос Y в модели «затраты-выпуск» (1.2), капитал K и труд L в модели (1.3) Кобба-Дугласа.

в моделях равно количеству эндогенных (независимых) переменных.
В моделях (1.1) и

(1.4) три эндогенные переменные (Yd, Ys, p) и соответственно три уравнения, в модели (1.2) количество уравнений равно количеству отраслей производственного сектора экономики, модель (1.3) состоит из одного уравнения по количеству независимых переменных (только выпуск продукции Y).
Второй принцип спецификации модели состоит в том, что количество уравнений в модели должно равняться количеству эндогенных переменных.

Этот принцип используется, в частности, для контроля за правильностью записи спецификации модели.

определения переменной р
Любая модель из нескольких уравнений может быть решена

относительно эндогенных переменных. Например модель (1.4) можно решить относительно Yd, Ys, p.

Откуда получается выражение для р

дохода, можно прогнозировать равновесную цену товара и уровень спроса и

предложения на него.

содержит более одной эндогенной переменной.
Определение. Уравнение модели имеет приведенную форму,

если оно содержит только одну эндогенную переменную.

Форма модели в виде системы нескольких уравнений считается структурной, если хотя бы одно из уравнений представлено в структурном виде.

На этапе спецификации модели из нескольких уравнений, как правило, имеют структурную форму.
Модель в виде изолированного уравнения всегда имеет приведенную форму.

Преобразование динамической модели к приведённой форме
Раздел

решения которой создаётся модель, присутствует фактор времени и он должен

найти отражение в спецификации модели (Третий принцип составления спецификации эконометрической модели).
Чтобы понять принцип отражения фактора времени в эконометрических моделях, рассмотрим снова спецификацию модели спроса-предложения товара на конкурентном рынке.

Датирование переменных в эконометрических моделях

следующих утверждениях экономической теории закреплено влияние фактора времени на текущие

значения спроса, предложения и цены товара на конкурентном рынке:

текущим располагаемым доходом (х) на душу населения, причём этот уровень

падает с ростом текущей цены и возрастает с увеличением текущего дохода;

2) текущее предложение объясняется ценой товара (р) в предшествующем периоде и возрастает с ростом этой цены;
Yd = Ys
3) текущее значение рыночной цены устанавливается при балансе текущего спроса и текущего предложения товара.

+ a1  · pt + a2  · xt,
ys= b0 + b1 · pt-1,
yd = ys
a1 

0, a2 > 0, b1 > 0.
Переменные (pt-1, xt), значения которых в периоде t известны, именуются предопределенными переменными

конкурентном рынке является структурной.
Модель служит

примером динамических моделей из линейных алгебраических уравнений.
Такие модели широко используются в эконометрике и именуются динамическими моделями из одновременных линейных уравнений.
Выше был приведен пример подробной записи таких моделей.

уравнений:

0 + 1 · pt-1 + 2 · xt;

P = 0  + 1 · pt-1 + 2 · xt ;

b1/ a1,
2 = -a2/a1.

Приведенная форма модели будет иметь вид

(относящуюся к одному периоду времени) взаимосвязь всех включенных в модель

переменных, то надобности в их датировании нет. Значения таких переменных принято именовать пространственными данными.

заданный период времени описывается количественными характеристиками (Y, C, I, G,

T, R).

Составить спецификацию макромодели, в которой величины (Yt, Ct, It) объясняются при помощи величин (Gt, Tt, Rt).

b2 · Rt,
Yt = Ct + It + Gt,

0 < a1 < 1, b1 > 0, b2 < 0.

В процессе составления спецификации необходимо учесть, что уровень инвестиций лучше объясняется лаговым значением ВВП и текущим значением ставки процента. После получения спецификации модели ее необходимо преобразовать к приведенной форме.

такое преобразование возможно. Для этого необходимо и достаточно, чтобы det

A  0.

Вычисляем
det A ={(-a1) · 0 · (-1) + 1 · 1 · 1 + (-1)  · 0 ·0}–{1 · 0 · 0 + (-1) · 1 · (-a1) + 0 · 1 · (-1)}= 1– a1.

Если 0 < a1 < 1, то det A  0

неучтённых факторов (Четвертый принцип)
Раздел

текущий спрос (и текущее предложение) неучтённых факторов?

Это принято

делать путём включения в поведенческие уравнения модели случайных переменных, значения которых рассеяны вокруг нуля. Такие случайные переменные принято называть случайными возмущениями или остатками.

vt,

,
a1 <0, a2 >0, b1 >0.

Ниже представлена спецификация «паутинной» модели спроса-предложения товара после включения в её поведенческие уравнения (первое и второе уравнения) случайных возмущений, соответственно ut и vt:

ut =ytd - (a0+ a1· pt + a2·xt)

= –A-1 · B - матрица коэффициентов приведённой формы модели,

- вектор случайных возмущений в приведённой форме модели.