Слайд 1Ekonometria
Wykład 5
dr hab. Małgorzata Radziukiewicz, prof. PSW Biała Podlaska
Слайд 2Jeśli jesteśmy w stanie zebrać wszystkich informacji na temat interesującej
nas zbiorowości wówczas do pełnego opisu wystarczą nam metody statystyki
opisowej.
W wielu jednak sytuacjach mówiąc o zbiorowości opieramy się na danych pochodzących z próby.
Aby prawidłowo uogólniać wyniki z próby na populację generalną należy stosować metody statystyki matematycznej.
Estymacja – po co i dlaczego?
Слайд 3Procedur uogólniania wyników z próby losowej na całą zbiorowość dostarcza
dział wnioskowania statystycznego.
Estymacja zatem to dział wnioskowania statystycznego będący zbiorem
metod pozwalających na uogólnianie wyników badania próby losowej na nieznaną postać i parametry rozkładu zmiennej losowej całej populacji oraz szacowanie błędów wynikających z tego uogólnienia.
Estymacja – po co i dlaczego?
Слайд 4W zależności od szukanej cechy rozkładu można podzielić metody estymacji
na dwie grupy:
Estymacja parametryczna - metody znajdowania nieznanych wartości
parametrów rozkładu
Estymacja nieparametryczna - metody znajdowania postaci rozkładu populacji
Слайд 5Wnioskowanie przybiera postać:
estymacji parametrów statystycznych czyli szacowania nieznanych wartości
parametrów np. średniej arytmetycznej w zbiorowości generalnej, odchylenia standardowego.
testowania hipotez,
które z kolei dotyczy weryfikacji przypuszczeń odnośnie określonego poziomu zmiennej losowej lub kształtu rozkładu w populacji generalnej.
Estymacja – po co i dlaczego?
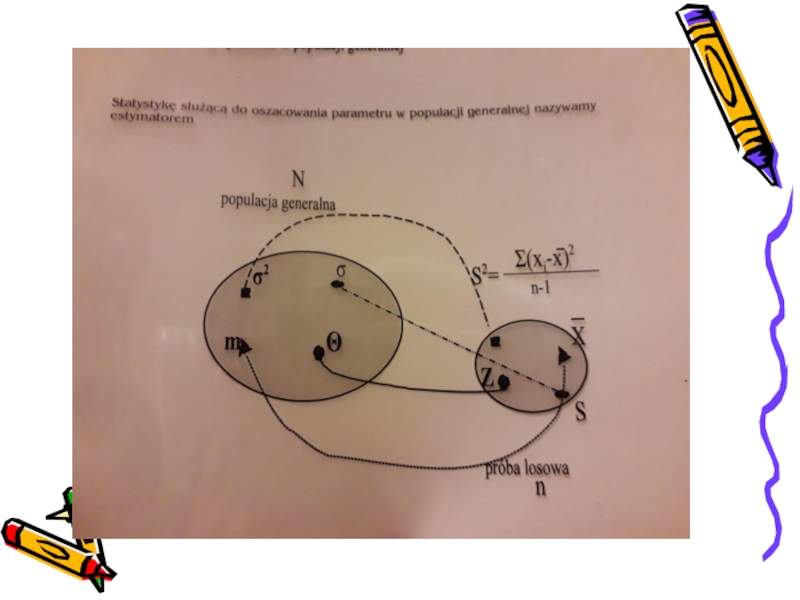
Слайд 6Zatem losujemy z N-elementowej populacji generalnej n-elementową próbę losową
Ze względu
na niemożność poznania parametru θ z populacji generalnej wnioskujemy o
wartości parametru θ w oparciu o zbadanie próby
Слайд 8dwa podejścia szacowania (estymacji)
1. punktowe szacowanie parametru θ (lub
innych parametrów populacji generalnej) – podajemy jedną liczbę odpowiadającą przypuszczalnej
wartości parametru
2. przedziałowe szacowanie parametru – podajemy pewien przedział, w którym przypuszczalnie znajduje się prawdziwa wartość parametru
Слайд 9Liczbą stanowiącą oszacowanie parametru θ musi być wartość jakiejś statystyki
obliczonej na podstawie próby
Слайд 11Estymator – wielkość (charakterystyka, miara), obliczona na podstawie próby, służąca
do oceny wartości nieznanych parametrów populacji generalnej.
Estymator – szacowany parametr
Слайд 12Estymator, jak każda statystyka z próby ma pewien rozkład.
Zadanie: -
jak dobrać estymator, aby jego rozkład gwarantował najlepsze oszacowanie?
Слайд 13Własności dobrego estymatora
Wartości, jakie może przyjmować estymator Z parametru θ
są różne dla różnych prób pochodzących z tej samej populacji;
Dlatego
też nie można oczekiwać, że otrzymany estymator Z będzie prawdziwą wartością estymowanego parametru θ;
Powstaje więc błąd losowy parametru θ, który dla danej próby jest różnicą między oceną parametru dokonaną na podstawie tej próby a prawdziwa wartością parametru:
ε = Z - θ
Слайд 14
Pożądane cechy estymatora
1. nieobciążoność – aby estymator dawał gwarancję, że
oszacowania nie będą w sposób systematyczny zaniżane ani zawyżane;
2. zgodność
– w miarę wzrostu próby (n) prawdopodobieństwo, że różnica między estymatorem a parametrem jest dowolnie małe, zbliża się do jedności;
3. efektywność – z 2-óch nieobciążonych estymatorów określonego parametru ten jest najefektywniejszy, który ma mniejszą wariancję.
Слайд 15 Estymator nieobciążony to ten, którego przeciętna wartość jest dokładnie
równa wartości szacowanego parametru tzn. zachodzi równość:
E( Zn) = θ
Innymi
słowy, przy wielokrotnym losowaniu próby średnia z wartości przyjmowanych przez estymator nieobciążony jest równa wartości szacowanego parametru.
Obciążoność oznacza, że oszacowania dostarczone przez taki estymator są obarczone błędem systematycznym
Estymator nieobciążony
Слайд 16Obciążoność oznacza, że oszacowania dostarczone przez taki estymator są obarczone
błędem systematycznym. Różnica:
Bn = E (Zn ) ) –
θ
nazywa się obciążeniem estymatora.
Jeżeli Bn > 0 to estymator Zn daje przeciętnie za wysokie oceny parametru θ;
Jeżeli Bn < 0 to estymator Zn daje przeciętnie za niskie oceny parametru θ.
Estymator obciążony
Слайд 17Jeśli spełniony jest warunek:
co jest równoważne warunkowi:
to estymator taki nazywa
się estymatorem asymptotycznie nieobciążonym.
Uwaga! Postulat nieobciążoności estymatora parametru oznacza praktyczne
żądanie, aby rozkład estymatora był scentrowany wokół prawdziwej wartości parametru, a więc by jego odchylenia od parametru miały charakter losowy.
Слайд 18Estymator Z parametru θ nazywa się estymatorem zgodnym, jeśli wraz
ze wzrostem liczebności próbki n jest on stochastycznie zbieżny do
wartości estymowanego parametru θ, tzn. jeśli jest spełniony warunek:
gdzie σ jest dowolnie mała liczbą dodatnią.
Zgodność estymatora Z oznacza, że wraz ze wzrostem liczebności próbki n, prawdopodobieństwo dowolnie małej różnicy między wartością estymatora Z a estymowanym parametrem θ dąży do 1.
Wynika stąd, że warto powiększyć próbkę, ponieważ przy wzroście n rośnie prawdopodobieństwo tego, że wartość estymatora parametru Z będzie się niewiele różnić od prawdziwej wartości estymowanego parametru θ, powodując tym samym mały błąd estymacji.
Estymator - zgodność
Слайд 19Estymator nieobciążony, który ma najmniejszą wariancję, nazywa się estymatorem najefektywniejszym.
Przy
estymacji punktowej sytuacja jest tym korzystniejsza, im wartość Zn oscyluje
bliżej σ, a więc im wariancja jest mniejsza.
Wyrażenie:
jest wariancją estymatora Zn.
Uwaga! Estymator jest tym efektywniejszy, im mniejsza jest jego wariancja i odchylenie standardowe.
Estymator - efektywność
Слайд 20Ze względu na formę wyniku estymacji wyróżniamy:
Estymacja punktowa –gdy szacujemy
liczbową wartość określonego parametru rozkładu cechy w całej populacji
Estymacja przedziałowa
–gdy wyznaczamy granice przedziału liczbowego, w których, z określonym prawdopodobieństwem, mieści się prawdziwa wartość szacowanego parametru.
Слайд 21Wprowadzenie do problematyki estymacji parametrów modeli ekonometrycznych
Problemy estymacji należą do
trudnych zagadnień;
Nie ma jednej uniwersalnej metody estymacji;
Strona rachunkowa metod estymacji
jest zawiła, więc dla większych modeli (z wieloma zmiennymi objaśniającymi) estymacja wymaga wykorzystania komputerów;
Estymacja jest jednym z najważniejszych działów statystyki matematycznej
Estymacja jest o tyle ważna, że od estymacji zależy jakość modelu ekonometrycznego i jego praktyczna użyteczność
Слайд 22Estymacja parametrów modelu ekonometrycznego
Przedmiotem estymacji w badaniu ekonometrycznym są parametry
sformułowanych wcześniej modeli ekonometrycznych
Ogólny zapis modelu ekonometrycznego:
Y= f(X1, X2 , ….,Xk , α1, α2,…,αk , ξ) (1)
gdzie:
Y- zmienna objaśniana;
X1, X2, ….., Xk – zmienne objaśniające
α1, α2 ,…., αk – parametry strukturalne modelu
ξ – składnik losowy
Слайд 29Estymacja parametrów modelu ekonometrycznego
Z reguły estymatory uzyskuje się w wyniku
zastosowania procedury numerycznej zwanej metodą najmniejszych kwadratów.
Estymatory mają wówczas pożądane
własności, o ile spełnione są pewne istotne założenia.
Założenia te dotyczą głównie:
- specyfikacji modelu i
- własności składnika losowego.
Слайд 30Założenia: model i dane
Założenie 1
Model jest liniowy względem parametrów
tj.:
Yt = α0 + α1 X1t + α2
X2t +..... + αk Xkt + ξt
gdzie t= 1,2,….n
Założenie 2
Zmienne objaśniające są nielosowe
Zmienna Y jest losowa, bowiem jest funkcją losowego ξ. Przyjmijmy Y- koszt produkcji, X – wartość produkcji. W modelu mogą zmieniać się rolami.
Uwaga! Niekonsekwencja klasycznej ekonometrii – w efekcie Y traktowana jest raz jako losowa a X nie i odwrotnie
Слайд 31Założenia: model i dane
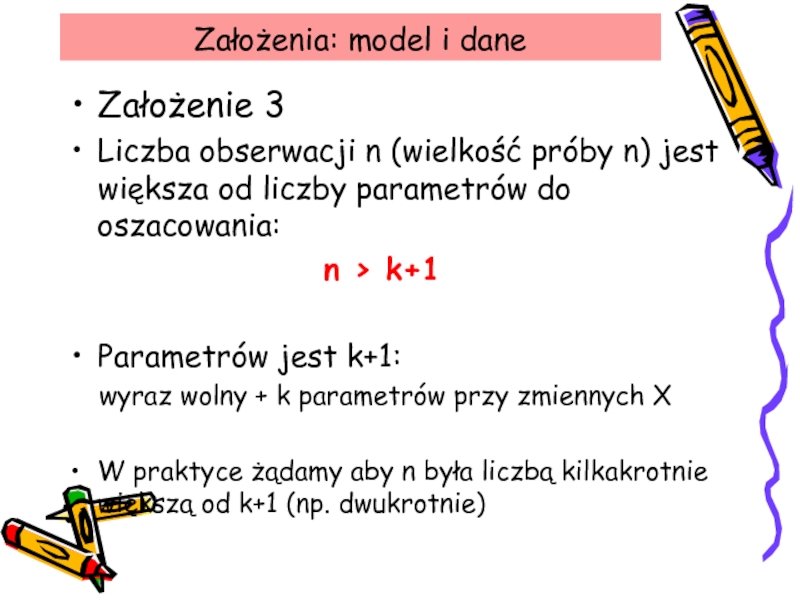
Założenie 3
Liczba obserwacji n (wielkość próby n)
jest większa od liczby parametrów do oszacowania:
n > k+1
Parametrów jest k+1:
wyraz wolny + k parametrów przy zmiennych X
W praktyce żądamy aby n była liczbą kilkakrotnie większą od k+1 (np. dwukrotnie)
Слайд 32Założenia: model i dane
Założenie 4
Żadna ze zmiennych nie jest kombinacją
liniową innych zmiennych objaśniających (włączając w ten zbiór także „sztuczną”
zmienną X0 = 1, która „stoi” przy wyrazie wolnym modelu)
Jest to założenie o braku współliniowości.
Nie istnieje zależność liniowa między wartościami z próby dla jakichkolwiek 2-óch, lub większej ilości zmiennych objaśniających.
Chodzi to, aby żadna ze zmiennych nie wnosiła do modelu tych informacji które już są wniesione przez inne zmienne.
Слайд 33Założenia: składnik losowy modelu
Założenie 5
Składnik losowy ξ jest zmienną losową
Składnik
losowy ma wartość oczekiwaną równa zeru dla wszystkich i=1,2,…., n:
E (ξi ) = 0
Oznacza to, że czynniki nie uwzględnione w modelu nie oddziałują w systematyczny sposób na średnią wartość zmiennej Y:
- wpływy dodatnie (+) i wpływy ujemne(-) „znoszą się” i w sumie efekt jest zerowy.
Слайд 34Założenia: składnik losowy modelu
Założenie 6
Składnik losowy ξ jest zmienną losową
Wariancja
zmiennej losowej ξi jest taka sama dla wszystkich obserwacji
D2 (ξi ) = σ2
dla i=1,2,…., n:
Przyjmujemy, że zmienne losowe mają jednakową dyspersję. Oznacza to, że wpływy na Y czynników nie ujętych w modelu mają takie same rozproszenie (niezależnie od numeru obserwacji)
Założenie o jednakowych wariancjach nosi nazwę założenia o homoscedastyczności.
Jego przeciwieństwem jest założenie o heteroscedastyczności (nierówna dyspersja)
Слайд 35Założenia: składnik losowy modelu
Założenie 7
Składnik losowy ξ jest zmienną losową
Zmienne
losowej ξi są nieskorelowane, czyli nie występuje autokorelacja składników losowych):
cov (ξi , ξj ) = σi,j (ξ) = 0 dla i≠j
i=1,2,…., n; j=1,2,…., n :
Oznacza to, że wpływy na Y czynników nie ujętych w modelu są nieskorelowane pomiędzy różnymi obserwacjami
Jest to założenie często niespełnione w modelach trendu
Слайд 36Założenia: składnik losowy modelu
Założenie 8
Każdy ze składników losowych ξi ma
rozkład normalny.
Biorąc pod uwagę założenia 4i 5 oznacza to, że
ξi ma rozkład N (0, σ2) dla i= 1,2,….,n
Niekiedy założenia 1-7 uzupełnia się o założenie 8 a model określa się wówczas mianem klasycznego modelu normalnej regresji liniowej
Założenie 8 ułatwia konstruowanie hipotez statystycznych służących weryfikacji modelu
Założenia dotyczace składnika losowego są nieznane, sprawdzone mogą być dopiero po oszacowaniu parametrów modelu
Слайд 37Model jest liniowy względem parametrów tj.:
Yt = α0
+ α1 X1t + α2 X2t +..... + αk Xkt
+ ξt
gdzie t= 1,2,….n
Wielkości parametrów αj (j= 0,1,2…,k) w modelu liniowym są niewiadomymi’
Po to by uzyskać wiedzę na temat wielkości parametrów modelu musimy posłużyć się danymi empirycznymi Y i Xk (k=1,2,….,n).
Na podstawie danych szacujemy nieznane parametry αi na postawie reakcji zmiennej zależnej na zmiany wielkości zmiennych niezależnych zaobserwowanych w próbie.
To co uzyskujemy na podstawie danych jest jedynie szacunkiem i będzie mniej lub bardziej dokładnym przybliżeniem prawdziwych wielkości parametrów αi.
W rezultacie oszacowania parametrów uzyskane na podstawie 2-óch prób z reguły będą różne.
Слайд 38Wniosek:
Oszacowania nielosowych parametrów są losowe.
Będąc jedynie niedokładnym przybliżeniem prawdziwych
wielkości parametrów mogą różnić się w zależności od wylosowanej próby.
Niedokładności
w oszacowaniach wielkości parametrów wynikają z zaburzeń losowych (ξ), które uniemożliwiają dokładne zmierzenie parametrów modelu.
Слайд 39Wartości dopasowane i reszty
Znajdowanie estymatorów (oszacowań) parametrów α0 , α1
.... αk
(j=0,1,2....k) określamy mianem regresji liniowej yi na x1i ,
…, xki .
Zgodnie z przyjętą konwencją oszacowania nieznanych parametrów α0 , α1 .... αk uzyskanych za pomocą MNK oznaczamy zwykle α0 , α1 .... αk .
Przewidywane na podstawie oszacowanego modelu wartości zmiennej zależnej Y nazywamy wartością teoretyczną (dopasowaną):
= a0 + a1 X1 + a2 X2 +..... + ak Xk
Wartości dopasowane różnią się od rzeczywistych wartości Y, ponieważ w modelu oszacowanym zamiast prawdziwych (nieznanych) wartości parametrów α0 , α1 .... αk używamy ich oszacowań α0 , α1 .... αk i pomijamy błąd losowy
Слайд 40Wartości dopasowane i reszty
Reszty definiujemy jako różnicę między wartością zaobserwowaną
zmiennej zależnej (objaśnianej) Y, a wartością dopasowaną tej zmiennej:
e =
Y- (a0 + a1 X1 + a2 X2 +..... + ak Xk )
e = Y- a0 - a1 X1 - a2 X2 -..... - ak Xk
Relację między resztami, obserwacjami i oszacowaniami parametrów można zapisać w sposób następujący:
= a0 + a1 X1 + a2 X2 +..... + ak Xk + e
Taki zapis pokazuje „pokrewieństwo” między α0 , α1 ... αk i a0 , a1 .... ak oraz między ξ i e.
Tak jak a0 , a1 .... ak są oszacowaniami α0 , α1 ... αk tak reszty e stanowią oszacowania składnika losowego ξ.
Uwaga! Reszty e nie są równe ξ
Слайд 41Wartości dopasowane i reszty
Model jest tym lepiej dopasowany, im mniejsza
jest odległość wartości teoretycznych od wartości obserwowanych
Najlepiej dopasowanym jest ten
model, w którym reszty są - co do wartości bezwzględnych – najmniejsze.
Estymator MNK znajdujemy, szukając takich a0 , a1.. ak dla których łączna odległość jest najmniejsza
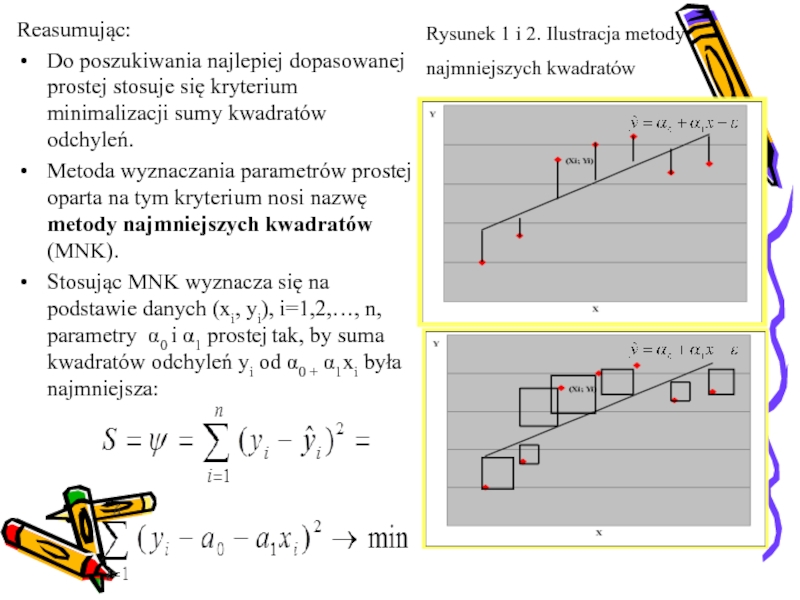
Слайд 42Rysunek 1 i 2. Ilustracja metody najmniejszych kwadratów
Reasumując:
Do poszukiwania
najlepiej dopasowanej prostej stosuje się kryterium minimalizacji sumy kwadratów odchyleń.
Metoda
wyznaczania parametrów prostej oparta na tym kryterium nosi nazwę metody najmniejszych kwadratów (MNK).
Stosując MNK wyznacza się na podstawie danych (xi, yi), i=1,2,…, n, parametry 0 i 1 prostej tak, by suma kwadratów odchyleń yi od 0 + 1xi była najmniejsza:
Слайд 43Mamy model liniowy z jedną zmienną objasniającą
Y = α0
+ α1 X1 + ξ
Wielkości parametrów αi (i= 0,1) w
modelu liniowym są niewiadomymi.
Po to, by uzyskać wiedzę na temat wielkości parametrów modelu musimy posłużyć się danymi empirycznymi.
Parametry αi (i= 0,1) szacujemy na podstawie danych:
Слайд 44Estymacja
Y jest wektorem zaobserwowanych wartości zmiennej objaśnianej:
Слайд 45Estymacja
● X jest macierzą zaobserwowanych wartości zmiennych objaśniających, przy czym
przyjmuje się, że w modelu obok wymienionych zmiennych występuje zmienna
x01=1 (przy parametrze α0), a więc:
Слайд 46Funkcja kryterium (minimalizujemy sumę kwadratów reszt e, przy czym reszty
to odchylenia wartości teoretycznych
od wartości empirycznych y) w zapisie skalarnym ma postać:
Слайд 47Estymacja
● Wektor ocen a parametrów strukturalnych α otrzymujemy obliczając pochodną
funkcji ψ względem wektora a i przyrównując ją do zera.
●
Wzór na wektor ocen parametrów strukturalnych przybiera ostatecznie postać:
● Podstawiając do wzoru:
Слайд 48Estymacja
● otrzymamy wektor ocen parametrów strukturalnych funkcji liniowej: