Слайд 1ЭЛЕКТРОННАЯ СТРУКТУРА ТВЕРДЫХ ТЕЛ
Твердое тело можно рассматривать как очень большую
молекулу, в которой соблюдается дальний или ближний порядок расположения атомов
или молекул. Дальний порядок отвечает идеально регулярным кристаллам, пространственная симметрия которых описывается 230 федоровскими группами. Ближний порядок характерен для реальных кристаллов с дефектами кристаллической решетки, аморфных тел, полимеров и т.д.: для них характерно проявление лишь локальной симметрии в определенных фрагментах структуры – кластерах. Для каждого из этих случаев существуют свои способы описания электронной структуры. Идеальные регулярные кристаллы рассматриваются как бесконечно протяженные (наличие поверхности игнорируется), и их электронные волновые функции определяются с явным учетом симметрии кристалла. Структуры некоторых идеальных атомных и молекулярных кристаллов представлены на рис.
В твердых телах с ближним порядком, нестехиометрических кристаллах и при изучении поверхностных эффектов часто достаточно использовать модифицированные молекулярные модели, выделив некоторый атомный или молекулярный кластер.

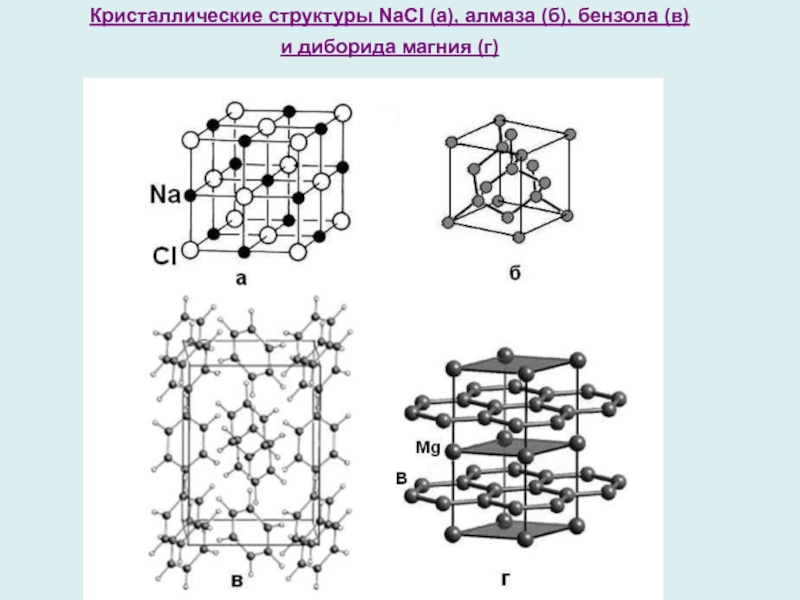
Слайд 2Кристаллические структуры NaCl (а), алмаза (б), бензола (в)
и диборида
магния (г)
Слайд 3Одноэлектронные волновые функции в бесконечных
периодических кристаллах и методы их расчета
Трансляционная
симметрия кристалла
В идеальном кристалле можно ввести три вектора трансляций a,
b и c так, что физические свойства кристалла в некоторой произвольно выбранной точке r точно воспроизводятся в любой другой точке r′ удовлетворяющей условию
r = r ′ + T = r′ + n1a + n2b + n3c,
где n1, n2, n3 − произвольные целые числа. Совокупность точек r, определяемая выражением (58), при различных n1, n2, n3 дает кристаллическую решетку, которая является геометрическим образом регулярного периодического расположения атомов в пространстве.
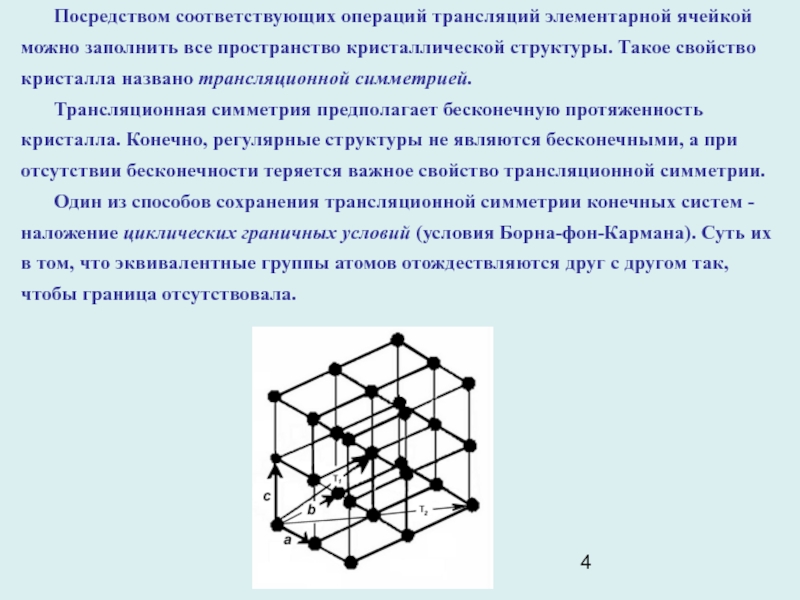
Параллелепипед, имеющий в качестве ребер векторы a, b и c , называется элементарной ячейкой кристалла. Перемещение в пространстве ячейки как целого, описываемое вектором T = n1a + n2b + n3c, называется трансляцией. Вектор трансляции связывает любые две соответственные точки кристаллической решетки (рис. 49). Посредством операций трансляции элементарной ячейкой можно заполнить все пространство кристаллической структуры. Такое свойство кристалла называется трансляционной симметрией.

Слайд 4Посредством соответствующих операций трансляций элементарной ячейкой можно заполнить все пространство
кристаллической структуры. Такое свойство кристалла названо трансляционной симметрией.
Трансляционная симметрия
предполагает бесконечную протяженность кристалла. Конечно, регулярные структуры не являются бесконечными, а при отсутствии бесконечности теряется важное свойство трансляционной симметрии.
Один из способов сохранения трансляционной симметрии конечных систем - наложение циклических граничных условий (условия Борна-фон-Кармана). Суть их в том, что эквивалентные группы атомов отождествляются друг с другом так, чтобы граница отсутствовала.
Слайд 5Электрон в периодическом поле кристалла
Рассмотрим случй одномерных систем. Для
цепочки точек, изображающих атомы, периодичность равносильна изгибу цепочки в окружность
большого радиуса и соединению между собой концевых точек.
Образование периодической системы на примере одномерной цепочки атомов с периодом а
Если движение электрона, например, вдоль оси х, ничем не ограничено (свободный электрон), его волновая функция есть бегущая волна eikx. Кинетическая энергия свободного электрона равна
Екин= p2/2m=(kh)2/8π2m,
(p – импульс, а λ− длина волны электрона), потенциальная энергия равна нулю, а волновое число k = 2π/λ может принимать любые значения.
Слайд 6Движение электрона ограничено в пространстве элементарной ячейкой кристалла. Граничные условия,
накладываемые на волновую функцию электрона: Ψ(0)=Ψ(а) = 0 (a –
размер ящика). Движение электрона в ящике можно описать как суперпозицию волн, бегущих в противоположных направлениях. Волновые функции различных состояний электрона, движущегося в периодическом пространстве, имеют вид
т.е. представляют собой стоячие волны. Из-за граничных условий волновое число и энергия электрона могут принимать лишь дискретные значения: k=± (π/а)n (n =1,2,3,…; n = 0 исключается как противоречащее условию нормировки волновых функций). Энергия электрона теперь зависит от волновых чисел и записывается следующим образом:
Слайд 7Стоячие волны, энергия которых пропорциональна u2, имеют узлы и пучности
в разных областях пространства по отношению к атомным остовам: каждая
из волн указывает места концентрации электронов в точках пространства, отвечающих различным значениям потенциальной энергии.
В случае нечетных n cos2[(π/а)nx]= 1 при x = а: стоячая волна u2 описывает концентрации электронов вблизи атомных остовов, где отрицательная потенциальная энергия взаимодействия «электрон-остов» максимальна по абсолютной величине.
В случае четных n функции u1 описывают концентрации электронов между остовами, где потенциальная энергия электрона не столь отрицательна. В среднем по периоду энергия волны u1 выше, а волны u2 – ниже, чем у бегущей волны, описывающей свободный электрон. Разность этих энергий, возникающая при ki=±(/а)ni как следствие трансляционной симметрии, называется энергетической щелью и обозначается Eg.
Рис. иллюстрирует сказанное для случая n = 1 и n = 2: поведение волновых функций позволяет заключить, что u2 соответствует связывающим, а u1 – разрыхляющим кристаллическим волновым функциям.

Слайд 8
В кристалле электроны движутся в трехмерном периодическом потенциале с периодом
a ~ 1 Å: V(r) = V(r + а), в
этом случае волновая функция электрона, обладающая трансляционными свойствами и являющаяся собственной функцией одноэлектронного гамильтониана, имеет вид
uk(r) = Neikrφk(r),
где φk(r) – периодическая в кристаллической решетке функция, N – нормировочный множитель. Одноэлектронная функция uk называется функцией Блоха. Кристаллические орбитали ϕk(r) – аналоги МО – строятся как линейные комбинации функций Блоха (62):
ϕk(r) = ∑ cj(k)ukj(r).
Функции Блоха ϕk(r), таким образом, играют в кристалле роль базисных функций.
Слайд 9
Вследствие трансляционной симметрии волновые функции электронов кристалла оказываются зависящими от
волновых векторов, пробегающих дискретные («разрешенные») значения. Энергии соответствующих электронных состояний
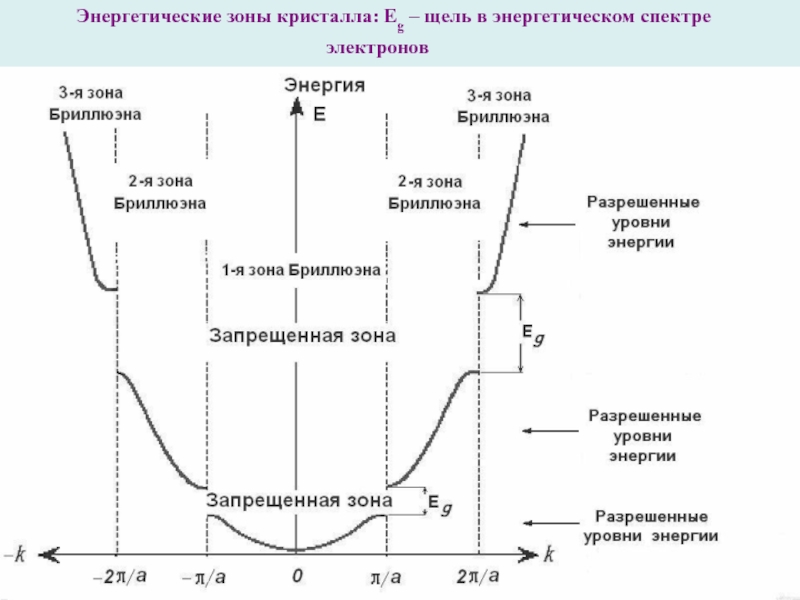
называются энергетическими уровнями, а их совокупности формируют энергетические полосы или энергетические зоны. Симметрия прямого пространства определяет симметрию пространства волновых векторов, которое называется обратным пространством. Важно, что в обратном пространстве также можно выделить наименьшую область, из которой операциями симметрии строится все обратное пространство. Эта область в k–пространстве называется первой зоной Бриллюэна; в одномерном случае она лежит между - π/a и +π/a (рис. 52). Зависимость энергии электронов от k в более высоких зонах Бриллюэна, охватывающих все k–пространство, получают из информации о первой зоне. Для этого достаточно сдвинуть кривую, описывающую эту зависимость, вдоль оси k на величину, кратную 2π/a (рис.). Такое представление называется схемой приведенных зон Бриллюэна.
Слайд 10Энергетические зоны кристалла: Еg – щель в энергетическом спектре электронов
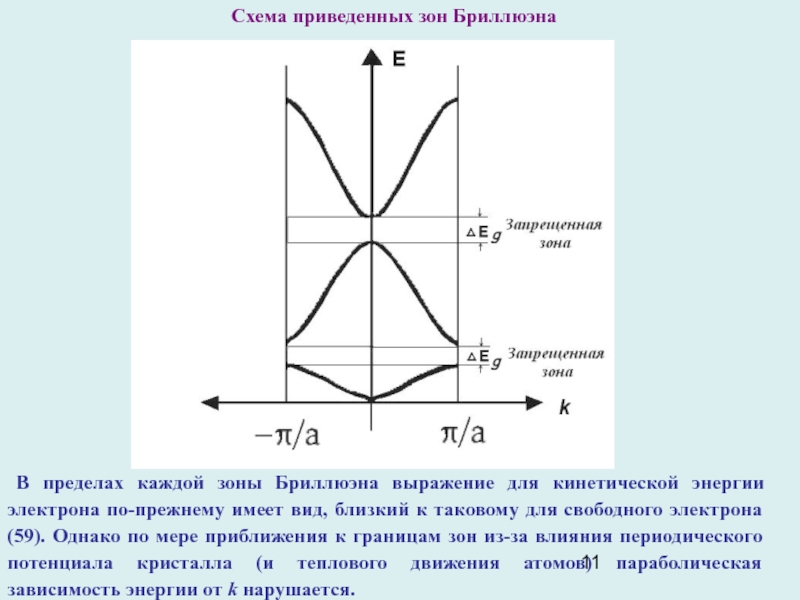
Слайд 11Схема приведенных зон Бриллюэна
В пределах каждой зоны Бриллюэна выражение
для кинетической энергии электрона по-прежнему имеет вид, близкий к таковому
для свободного электрона (59). Однако по мере приближения к границам зон из-за влияния периодического потенциала кристалла (и теплового движения атомов) параболическая зависимость энергии от k нарушается.
Слайд 12Схема образования s- и p-зон в щелочных металлах
Число разрешенных
значений волнового вектора k в каждой зоне Бриллюэна, при которых
функция Блоха uk(x) отлична от нуля, определяется числом элементарных ячеек кристаллической решетки М и числом атомов в одной ячейке σ; оно равно М·σ. Рис. 54 иллюстрирует процесс формирования верхней заполненной электронами s-зоны и первой свободной p-зоны в одновалентных щелочных металлах (Li, Na, K, Rb, Cs). Если рассматриваемый уровень энергии в атоме имеет (2l+1)-кратное вырождение, то соответствующая энергетическая зона в кристалле состоит из (2l+1) подуровней. Уровни в каждой зоне расположены довольно близко друг к другу: при ширине зоны ~ 1 эВ, расстояние между уровнями составляет ~ 10-22 эВ. Это настолько мало, что можно считать зоны непрерывными.
Слайд 13При абсолютном нуле электроны кристалла в основном состоянии последовательно занимают
уровни, начиная с наименьшего по энергии уровня (nx = ny
= nz = 0) до некоторого граничного. Каждый энергетический уровень, вследствие принципа Паули, может быть занят двумя электронами с противоположными спинами. Высший энергетический уровень, заполненный электронами в твердом теле, называется уровнем Ферми, а его энергия – энергией Ферми. Симметрия обратной решетки кристалла в общем случае такова, что kx ≠ ky ≠ kz , а число занятых электронных состояний с максимальными величинами k в разных кристаллах различно, поэтому говорят о поверхности Ферми, которая может иметь весьма сложный вид в k-пространстве. Примеры поверхности Ферми различных металлов показаны на рис.
Поверхности Ферми различных металлов
Слайд 15 Электронные свойства твердых тел зависят от их состава
и химической связи. Два предельных случая, которые типичны для металлов.
1) Валентные электроны находятся на внешних s- и p-орбиталях, которые слабо связаны с атомными остовами. Интерференция волновых функций велика и валентные s- и p-электроны коллективизируются и приобретают способность перемещаться в кристаллической решетке. Такие электроны в первом приближении можно считать почти свободными и описывать плоскими волнами, слабо модифицированными периодическим потенциалом решетки. Это приближение в физике твердого тела называют приближением слабой связи.
2) Валентные электроны находятся на внутренних 3d-, 4d-, 5d- и 4f-электронных оболочках, размеры которых существенно меньше, чем внешних s- и p-орбиталей. Интерференция d- и f-орбиталей слабая и локализация d- и f-электронов сохраняется почти в той же степени, что и в атомах. В этом случае для описания волновых функций применяется приближение ЛКАО, которое в физике твердого тела называют приближением сильной связи. Это приближение хорошо описывает непереходные металлы с заполненными электронами внутренними d- и f-оболочками, а также переходные и редкоземельные металлы.

Слайд 16Два основных метода расчета одноэлектронных волновых функций в кристаллах: -
Метод Хартри-Фока-Рутана. Функции (62) используются как базисные, а периодические в
кристаллической решетке функции φk(r) представляют собой локализованные атомные орбитали (приближение сильной связи), которые строятся из гауссовых орбиталей. Метод переоценивает ширину запрещенной зоны в 1,5-2 раза и неприменим для расчета Ферми-поверхности металлов.
- Метод Кона-Шэма относится к группе методов функционала плотности, основанных на предположении, что электронную плотность можно рассматривать как неоднородный электронный газ. Кинетическая энергия электронов описывается в приближении независимых частиц, а обменные и корреляционные эффекты учитываются с помощью выражений, полученных при анализе свойств однородного электронного газа и модифицированных с учетом неоднородности ЭП. Одноэлектронные уравнения Кона-Шэма имеют вид (в атомных единицах)
[-1/2∇2+VN(r)+∫ρ(r′)/(r-r′)dr′+Vxc]ϕjk(r)=Ej(k)ϕjk(r) .
Здесь VN –потенциал ядер, ρ(r) – электронная плотность, а Vxc – обменно-корреляционный потенциал; индекс j нумерует уровни с энергией Ej(k). Базисные функции могут строиться из атомных орбиталей, наборов плоских волн, а также из их комбинаций. Недостатком этого метода является недооценка ширины запрещенной зоны.

Слайд 17Зонная структура и свойства твердых тел
Электроны в кристалле оказываются распределенными
по энергетическим зонам, состоящим из уровней энергии, отвечающих волновым функциям
с разрешенными симметрией волновыми векторами. Свойства этих зон зависят от квантовых чисел образующих их электронов и от химической связи между атомами. Расстояния между ними на краях зоны меньше, чем в середине. Из-за этого плотность разрешенных уровней (число уровней в единичном интервале энергии) не одинакова по всей зоне: у краев зоны плотность выше. Важной характеристикой является функция Е(k), которая описывает закон дисперсии энергии внутри зоны Бриллюэна. Ее называют структурой зоны (полосы) и считают непрерывной. Распределение энергетических уровней в зоне характеризует плотность состояний:
g(E) = dN(E)/dE Можно показать, что при 0 К g(E) ~ √E; при температурах, отличных от нуля, эта зависимость носит более сложный характер (рис. 56): распределение энергетических уровней в разных зонах различно, а функция g(E) отлична от параболы Интегрирование функции g(E) по dE до уровня Ферми дает полное число занятых электронами кристаллических орбиталей N.

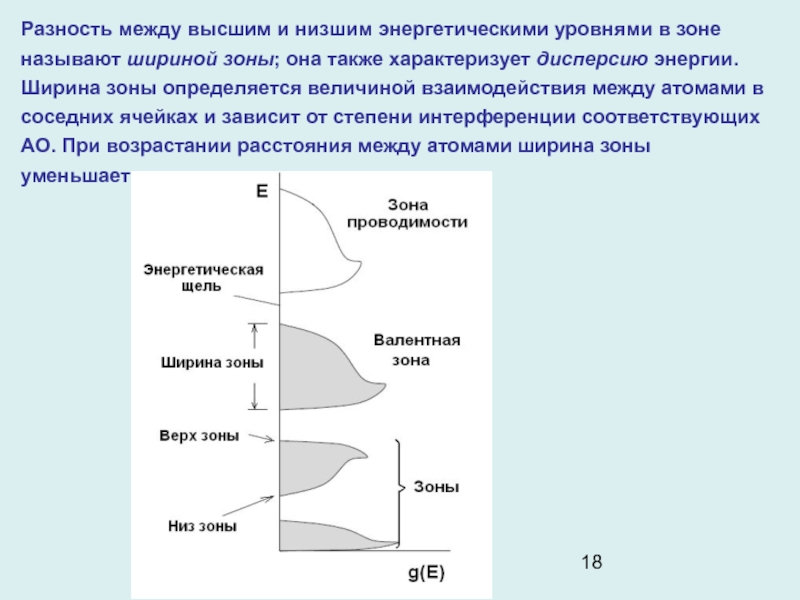
Слайд 18Разность между высшим и низшим энергетическими уровнями в зоне называют
шириной зоны; она также характеризует дисперсию энергии. Ширина зоны определяется
величиной взаимодействия между атомами в соседних ячейках и зависит от степени интерференции соответствующих АО. При возрастании расстояния между атомами ширина зоны уменьшается.
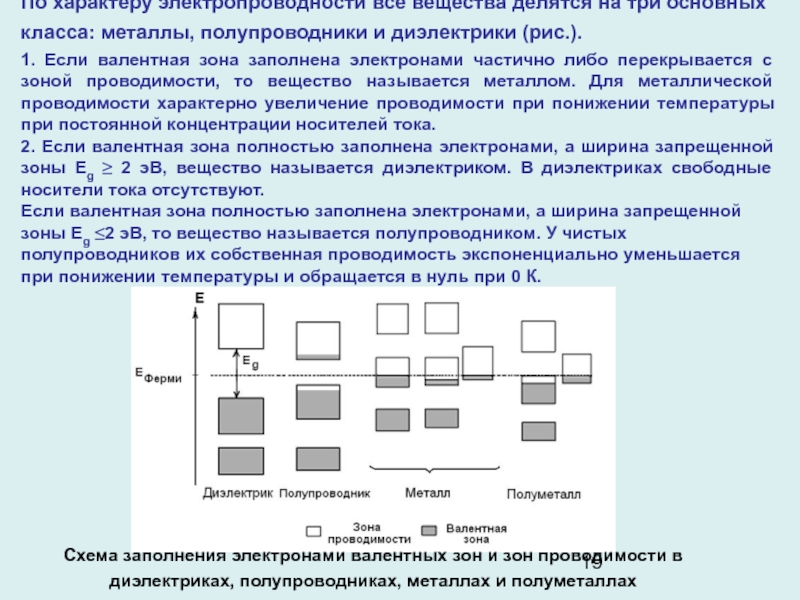
Слайд 19Схема заполнения электронами валентных зон и зон проводимости в диэлектриках,
полупроводниках, металлах и полуметаллах
По характеру электропроводности все вещества делятся
на три основных класса: металлы, полупроводники и диэлектрики (рис.).
1. Если валентная зона заполнена электронами частично либо перекрывается с зоной проводимости, то вещество называется металлом. Для металлической проводимости характерно увеличение проводимости при понижении температуры при постоянной концентрации носителей тока.
2. Если валентная зона полностью заполнена электронами, а ширина запрещенной зоны Еg ≥ 2 эВ, вещество называется диэлектриком. В диэлектриках свободные носители тока отсутствуют.
Если валентная зона полностью заполнена электронами, а ширина запрещенной зоны Еg ≤2 эВ, то вещество называется полупроводником. У чистых полупроводников их собственная проводимость экспоненциально уменьшается при понижении температуры и обращается в нуль при 0 К.
Слайд 20Кластерная модель
Часто ( например, при расчетах нестехиометрических кристаллов) целесообразно
рассчитать лишь некоторый атомный или молекулярный фрагмент кристалла – кластер.
Основной метод, используемый для это цели– метод Хартри-Фока.
Одна из распространенных его кластерных модификаций – так называемый Xα-метод. Корреляция электронов по-прежнему игнорируется, а обменный потенциал представляется в виде
Vx(r ) = -3α((3/8π)ρ(r ))1/3 (10)
Несмотря на кажущуюся переупрощенность, Xα-метод дает хорошее количественное описание не только локализованных состояний, но и зонной структуры твердых тел. Для этого используют метод «погруженного» кластера: одноэлектронные функции раскладывают по базису из локализованных орбиталей и функций Блоха. Метод успешно применяется для изучения магнитных свойств веществ, химической связи и др.