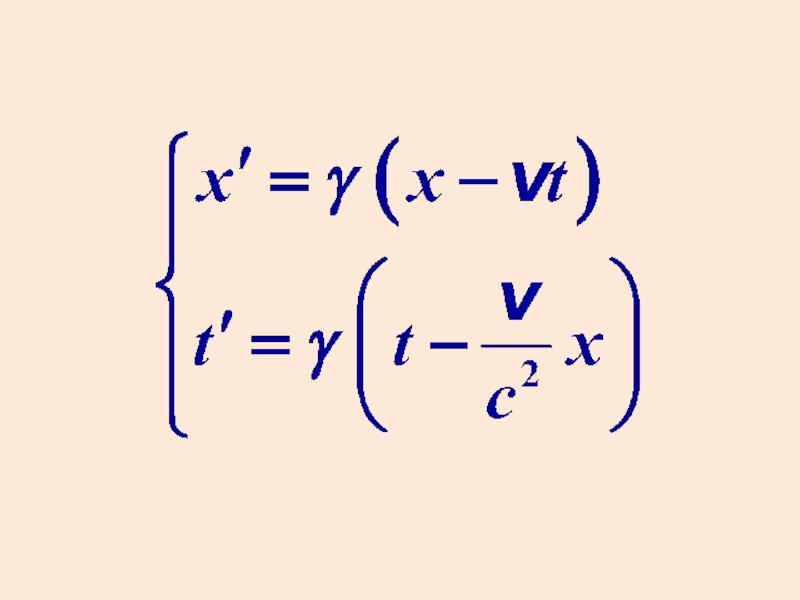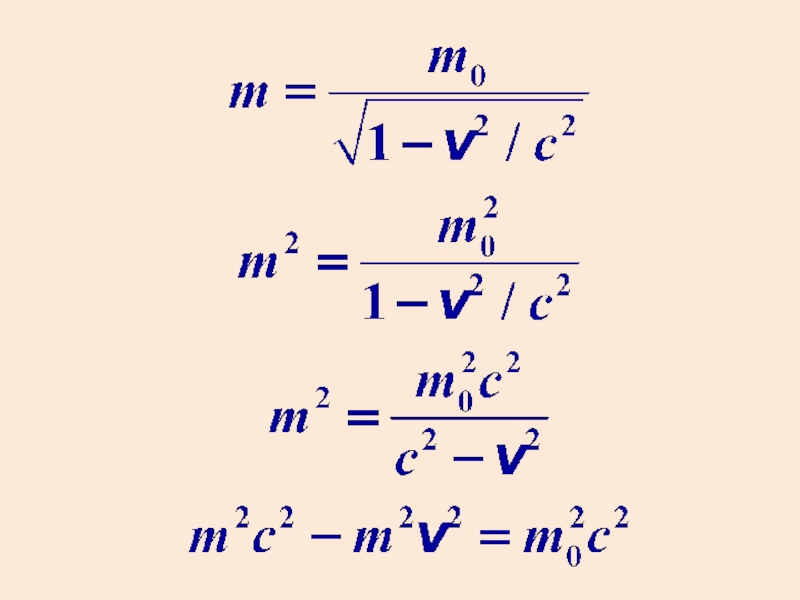Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ МЕХАНИКИ (СТО)
Содержание
- 1. ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ МЕХАНИКИ (СТО)
- 2. Релятивистская механика изучает движение тел со скоростями
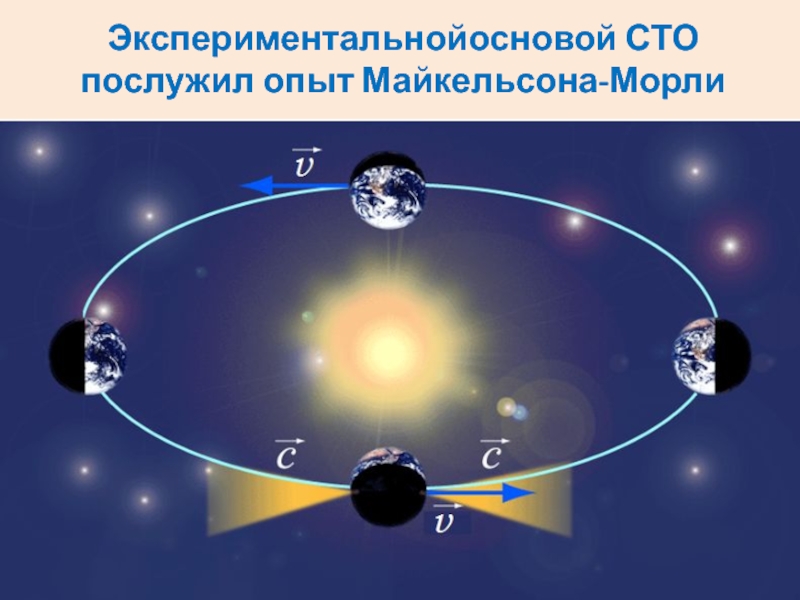
- 3. Экспериментальнойосновой СТО послужил опыт Майкельсона-Морли
- 4. Слайд 4
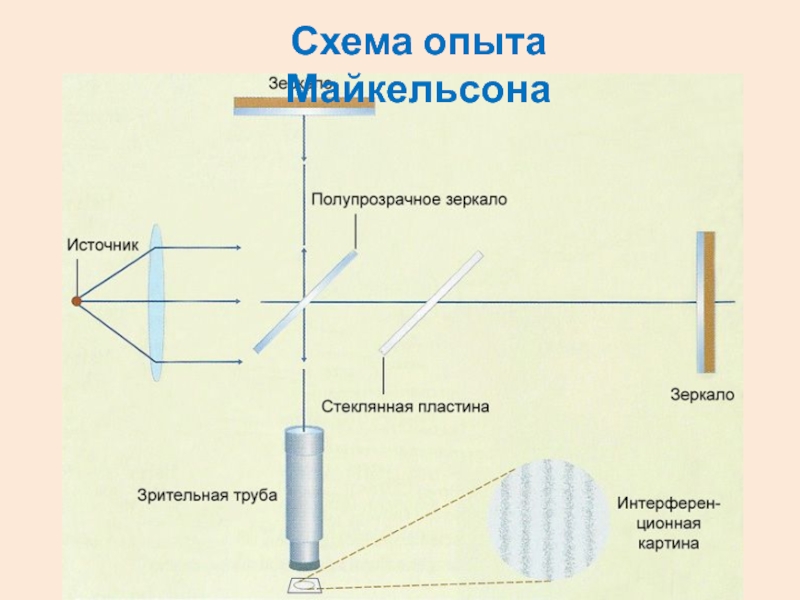
- 5. Схема опыта Майкельсона
- 6. Кажется, что в направлении движения Земли скорость
- 7. Альберт Эйнштейн (1879 – 1955)— один из
- 8. Постулаты СТОПервый постулат (релятивистский принцип относительности)В любых
- 9. Второй постулат (принцип инвариантности скорости света в
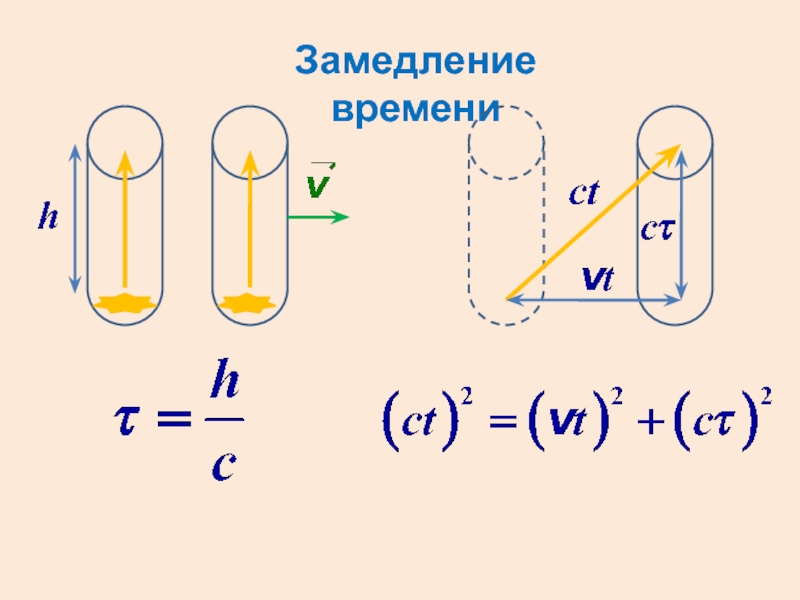
- 10. Замедление времени
- 11. Ход времени в движущейся СО замедляетсяτ – собственное время системы
- 12. Обозначимтогда
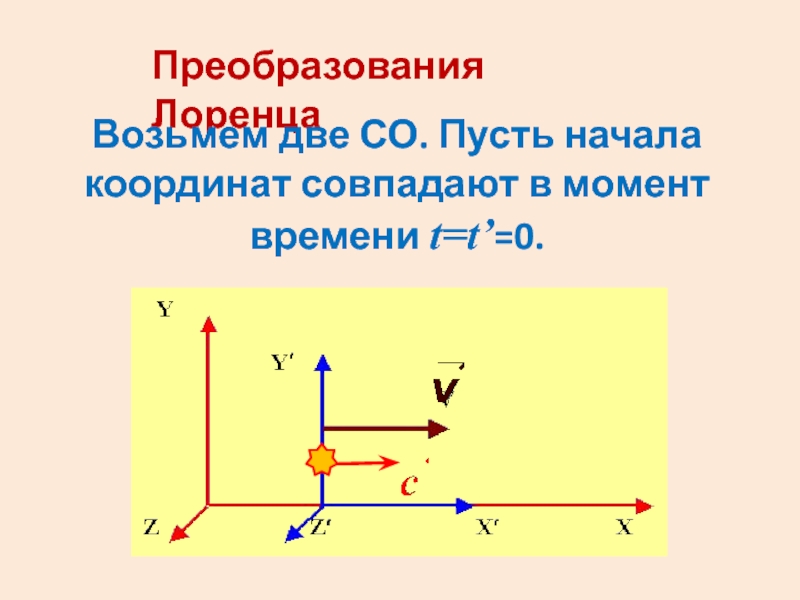
- 13. Преобразования ЛоренцаВозьмем две СО. Пусть начала координат совпадают в момент времени t=t’=0.
- 14. По Галилею скорость луча в СО К’
- 15. Хендрик Антон Лоренц (1853-1928) — голландский физик-теоретик.
- 16. Слайд 16
- 17. Лоренцево сокращениеПусть наблюдатель из системы К измеряет
- 18. Слайд 18
- 19. Если положения концов отмечены одновременно, то
- 20. Линейный размер тела уменьшается в направлении движения.
- 21. ОдновременностьНайдем промежуток времени между двумя событиями в системе К’.
- 22. Если два события произошли одновременно в разных
- 23. Пространственно-временной интервалСогласно СТО любое событие происходит в
- 24. Из преобразований Лоренца следует, что интервал между
- 25. Релятивистское сложение скоростейЗапишем преобразования Лоренца для бесконечно малого промежутка времени.
- 26. Скорость тела в системе КРазделив каждый член дроби на dt’, получимu’- скорость тела в системе К’
- 27. Пусть u’=c, тогдаСкорость света в обеих СО одинакова!
- 28. Релятивистские масса и импульсЧтобы закон сохранения импульса
- 29. Величину m0 называют массой покоя.m – масса движущегося тела.
- 30. Тогда релятивистский импульс:
- 31. Основной закон РМКак и у Ньютона, скорость изменения импульса равна равнодействующей силе.
- 32. Найдем ускорение тела
- 33. В общем случае ускорение тела не совпадает
- 34. Энергия в РМВычислим кинетическую энергию тела. Ее
- 35. Слайд 35
- 36. ДифференцируемТогда
- 37. Полная энергияЭнергия покояКинетическая энергия
- 38. Согласно Эйнштейну, находящаяся в покое масса содержит
- 39. Кинетическая энергия может превращаться в массу покоя
- 40. Связь релятивистских энергии и импульса
- 41. Скачать презентанцию
Релятивистская механика изучает движение тел со скоростями близкими к скорости света с. Классическая (ньютонова) механика – частный случай релятивистской механики.
Слайды и текст этой презентации
Слайд 6Кажется, что в направлении движения Земли скорость распространения света должна
быть наибольшей. Опыт же показал, что во всех направлениях скорости
равны.Это противоречие устранила теория относительности Эйнштейна.
Слайд 7Альберт Эйнштейн (1879 – 1955)
— один из наиболее значительных физиков
XX века, создатель специальной и общей теории относительности, лауреат Нобелевской
премии по физике (1921).
Слайд 8Постулаты СТО
Первый постулат
(релятивистский принцип относительности)
В любых ИСО все физические
явления (механические, электрические, магнитные, световые и др.) при одних и
тех же условиях протекают одинаково, т. е. невозможно установить, движется ли данная СО равномерно прямолинейно или покоится.
Слайд 9Второй постулат
(принцип инвариантности скорости света в вакууме)
Скорость света в
вакууме не зависит от скоростей движения источника и приёмника.
Она
одинакова во всех ИСО. 
Слайд 13Преобразования Лоренца
Возьмем две СО. Пусть начала координат совпадают в момент
времени t=t’=0.
Слайд 14По Галилею скорость луча в СО К’ равна с, а
в СО К с+v.
Надо в обеих СО получить скорость луча
равную с, чтобы Эту задачу решил Лоренц.
Слайд 15Хендрик Антон Лоренц (1853-1928) — голландский физик-теоретик. Лауреат Нобелевской премии
по физике (1902) и других наград, член Нидерландской королевской академии
наук (1881), ряда иностранных академий наук и научных обществ.
Слайд 17Лоренцево сокращение
Пусть наблюдатель из системы К измеряет длину движущейся относительно
него линейки.
В системе К’ линейка неподвижна. Ее длина
Слайд 20Линейный размер тела уменьшается в направлении движения.
Поперечные размеры тела
не зависят от скорости его движения и одинаковы во всех
ИСО.
Слайд 22Если два события произошли одновременно в разных точках неподвижной системы
отсчета, они будут неодновременными в движущейся системе отсчета.
Слайд 23Пространственно-временной интервал
Согласно СТО любое событие происходит в четырёхмерном пространстве с
координатами x, y, z, t.
Интервалом между двумя событиями называется величина
Слайд 24Из преобразований Лоренца следует, что интервал между двумя событиями не
изменяется при переходе от движущейся ИСО к неподвижной.
Слайд 25Релятивистское сложение скоростей
Запишем преобразования Лоренца для бесконечно малого промежутка времени.
Слайд 26Скорость тела в системе К
Разделив каждый член дроби на dt’,
получим
u’- скорость тела в системе К’
Слайд 28Релятивистские масса и импульс
Чтобы закон сохранения импульса не нарушался при
переходе к другой ИСО, необходимо учесть зависимость массы от скорости:
Как
и в классической механике
Слайд 33В общем случае ускорение тела не совпадает по направлению с
силой. Величина и направление ускорения определяются не только силой, но
также и скоростью тела.
Слайд 34Энергия в РМ
Вычислим кинетическую энергию тела.
Ее приращение равно работе
равнодействующей силы.
Последнюю величину найдем из формулы для релятивистской массы.
Слайд 38Согласно Эйнштейну, находящаяся в покое масса содержит огромный запас энергии.
Первое
экспериментальное подтверждение этому было получено при сравнении энергии, выделяющейся при
радиоактивном распаде, с разностью масс исходного ядра и конечных продуктов.
Слайд 39Кинетическая энергия может превращаться в массу покоя и наоборот.
Полная энергия
замкнутой системы сохраняется, следовательно сохраняется и ее релятивистская масса.
