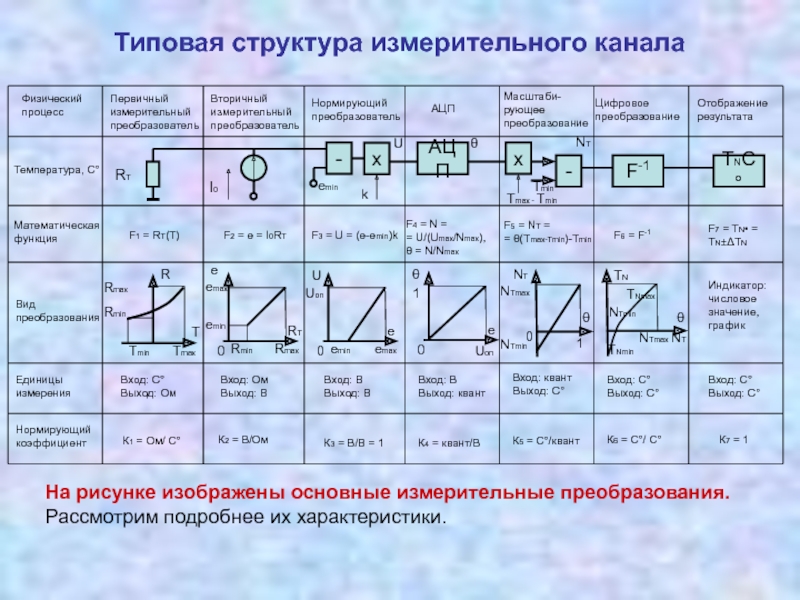
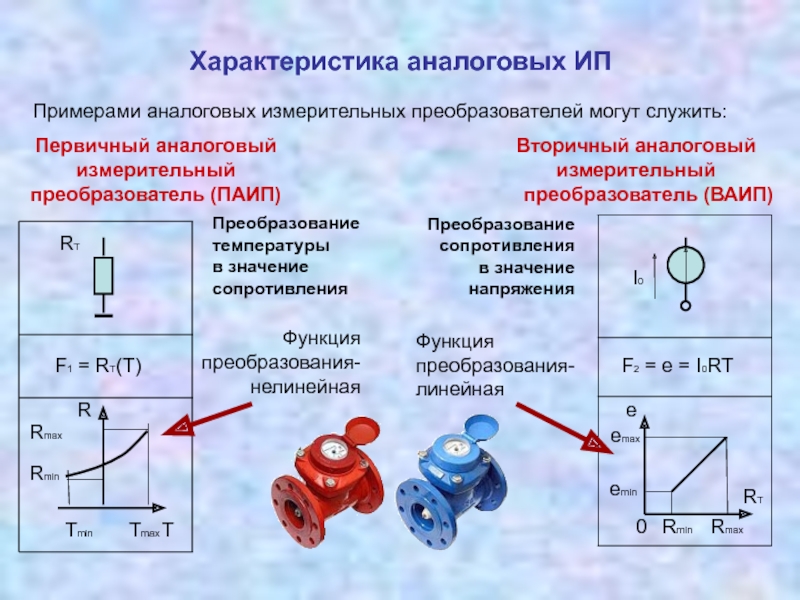
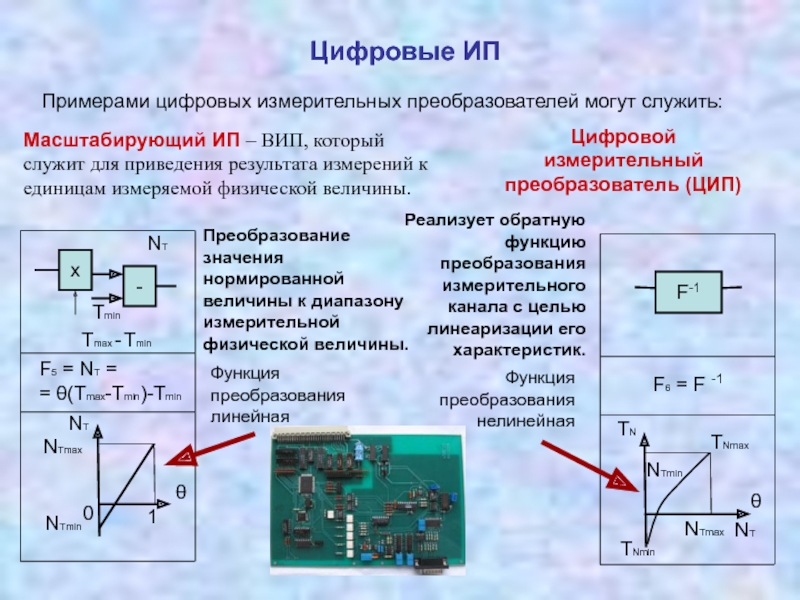
преобразователей
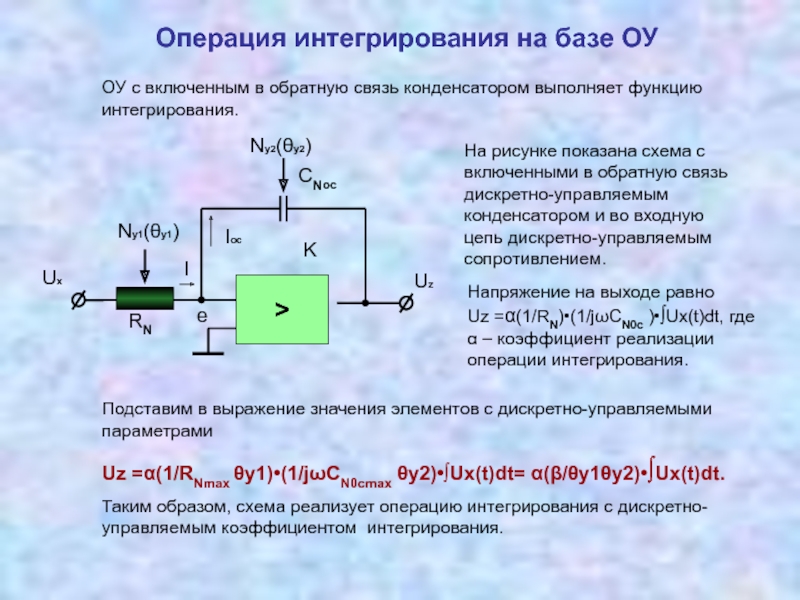
3.3 Функциональные измерительные преобразователи с дискретно управляемыми параметрами
3.4
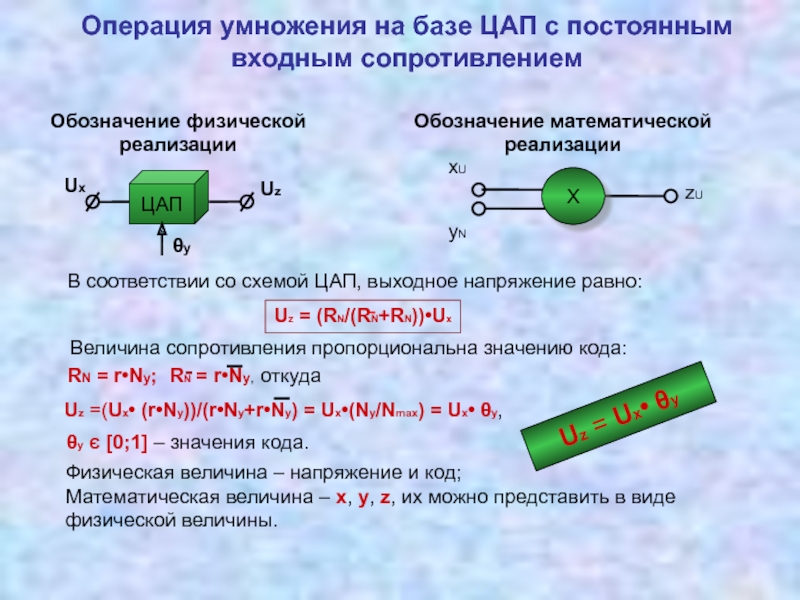
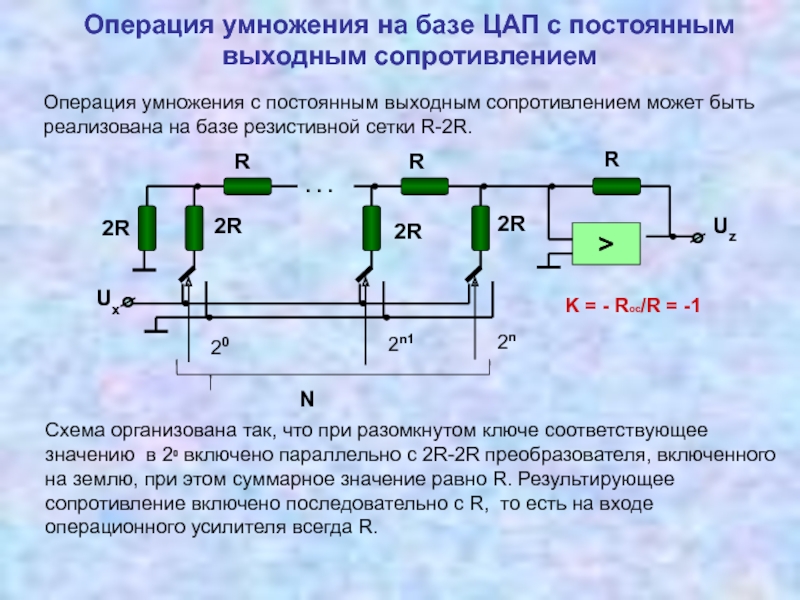
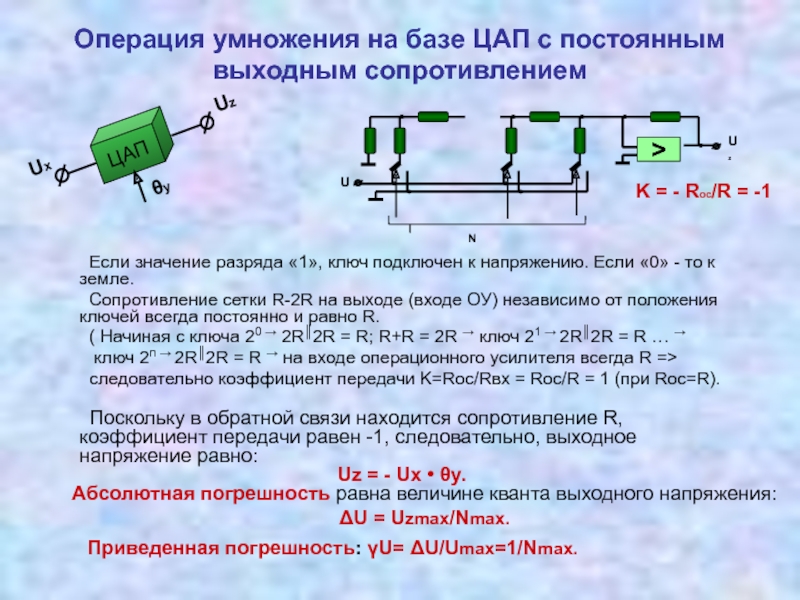
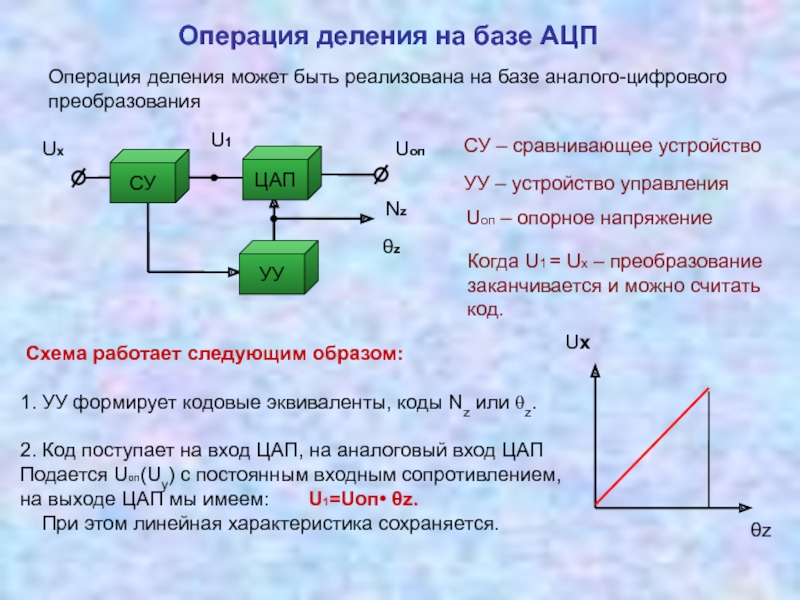
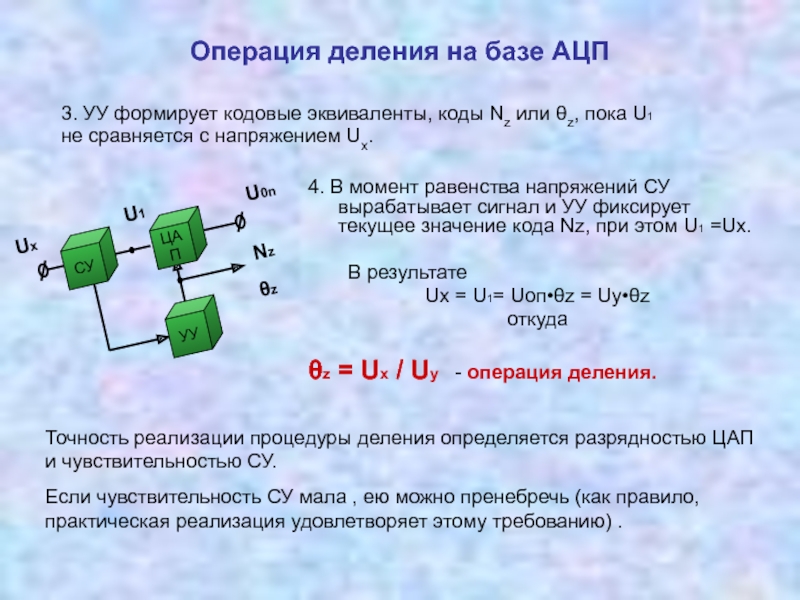
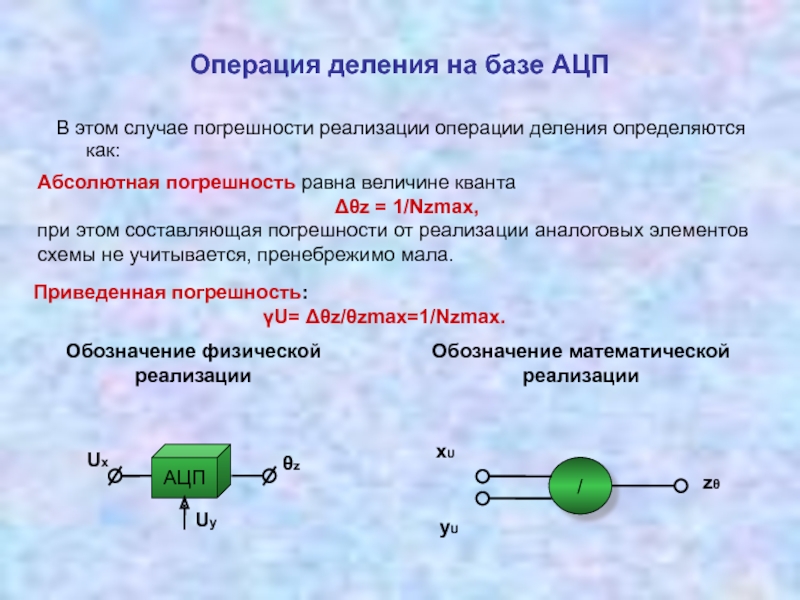
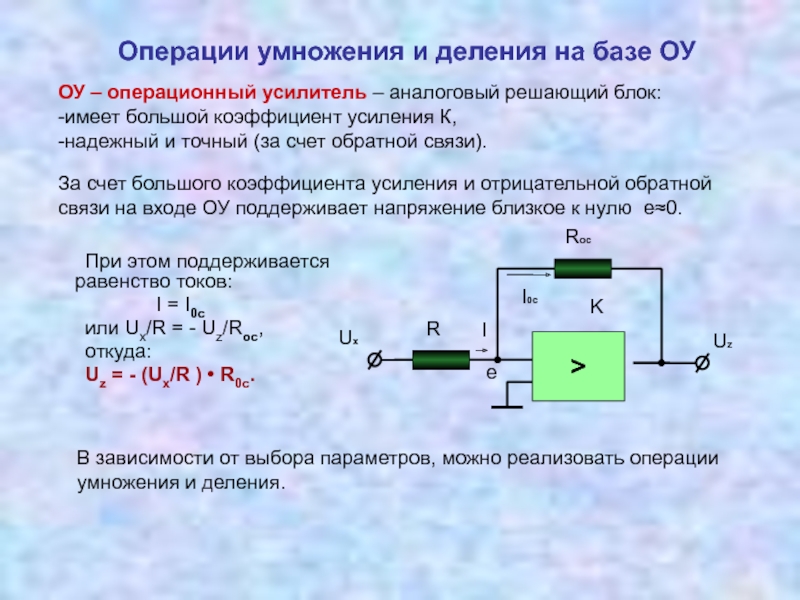
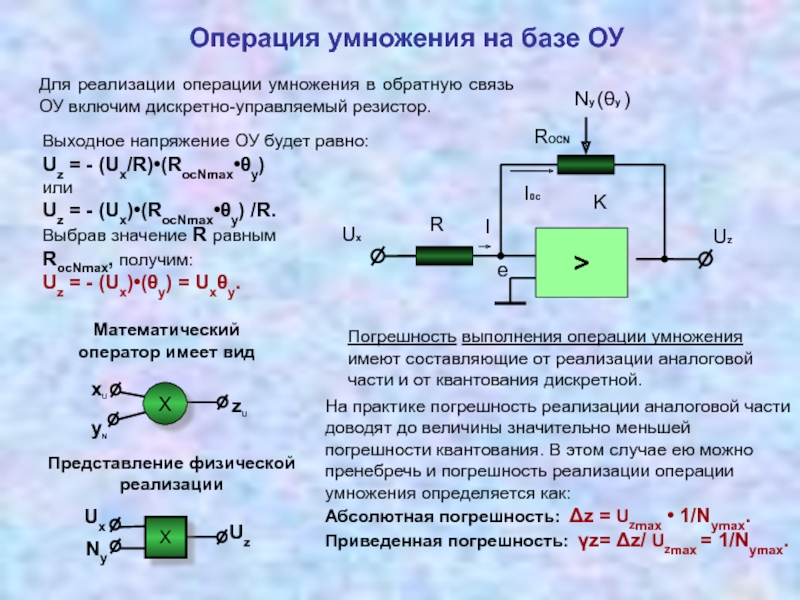
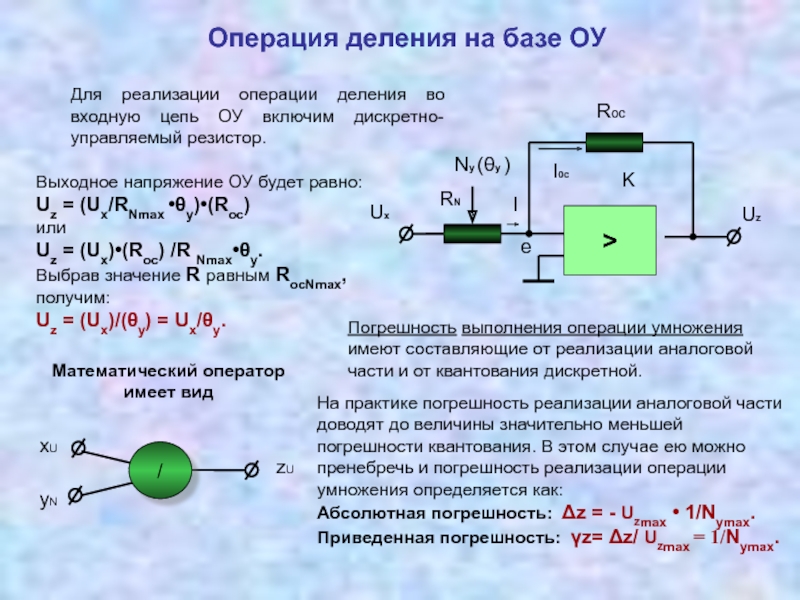
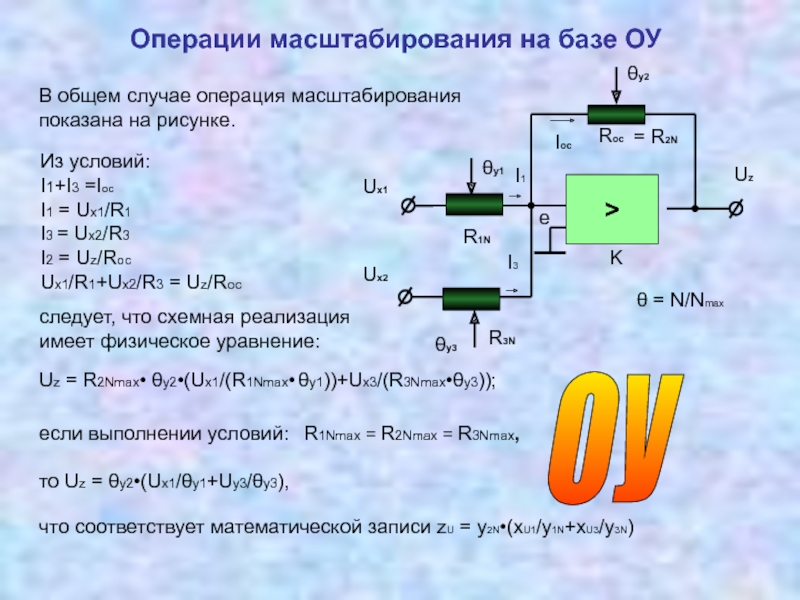
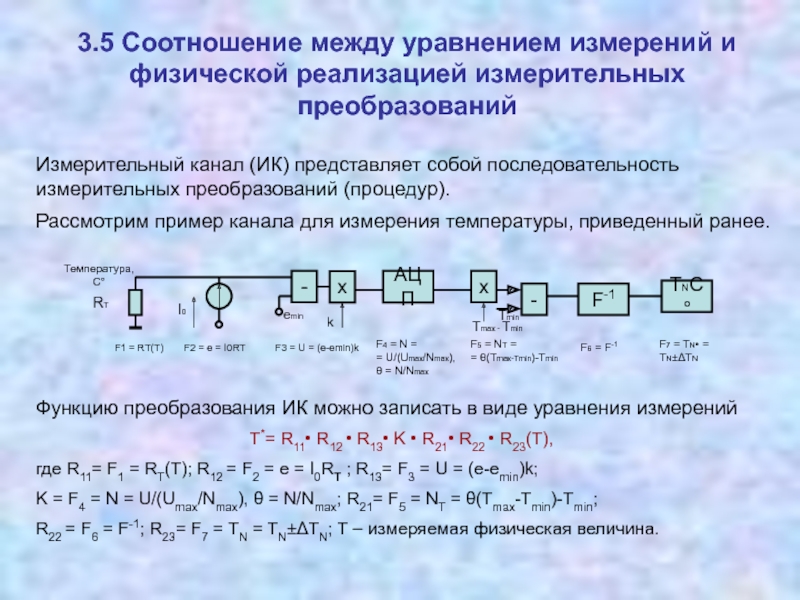
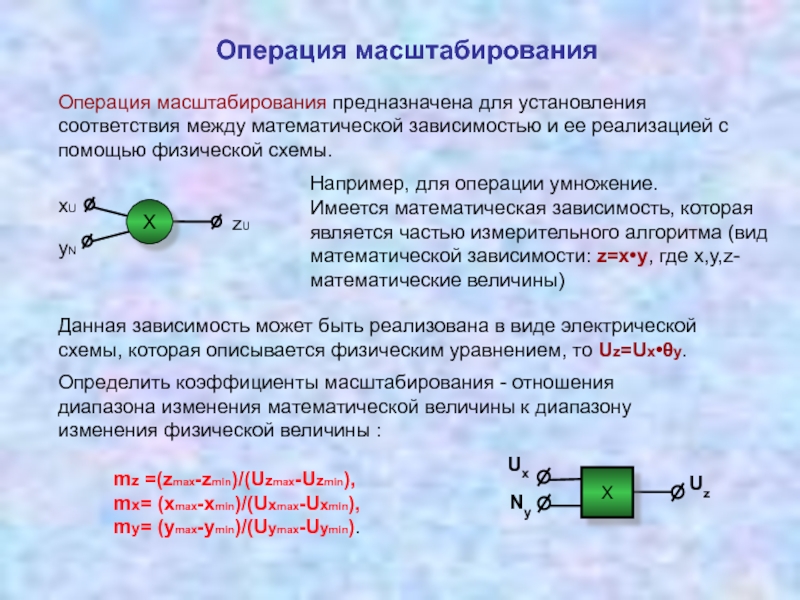
Измерительные преобразователи, реализующие операции умножения, деления 3.5 Соотношение между уравнением измерений и физической реализацией измерительных преобразований
3.6 Анализ погрешностей при реализации измерительного канала