Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Инженерная и компьютерная графика
Содержание
- 1. Инженерная и компьютерная графика
- 2. Литература 1.В.М. Дегтярев, В.П. Затыльникова. Инженерная и
- 3. Инженерная и компьютерная графикаРаздел1: начертательная геометрияПроецирование прямой линии
- 4. 2. Проекции прямой линии 2.1 Проекции прямой
- 5. 2.1 Проекции прямой общего положения (продолжение)1. Прямая
- 6. Эпюр прямой общего положения Восходящая прямая Нисходящая прямая
- 7. 2.2 Проекции прямых частного положения 2.2.1 Проекции
- 8. 2.2 Проекции прямых частного положения 2.2.2 Проекции
- 9. 2.3 Взаимное положение точки и прямойТочка С
- 10. 2.3.1 Положение точки относительно профильной прямойТочка Е
- 11. 2.4 Деление отрезка в заданном отношенииЗадача: Разделить
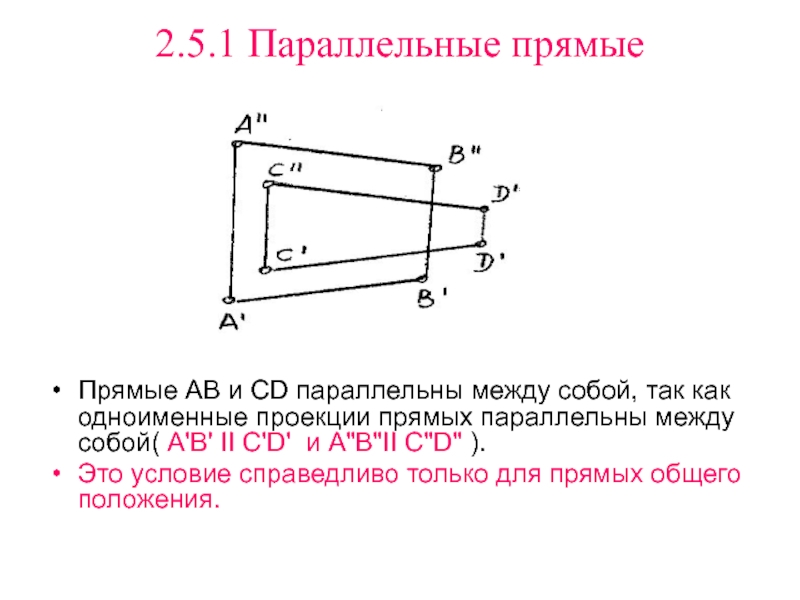
- 12. 2.5.1 Параллельные прямыеПрямые АВ и СD параллельны
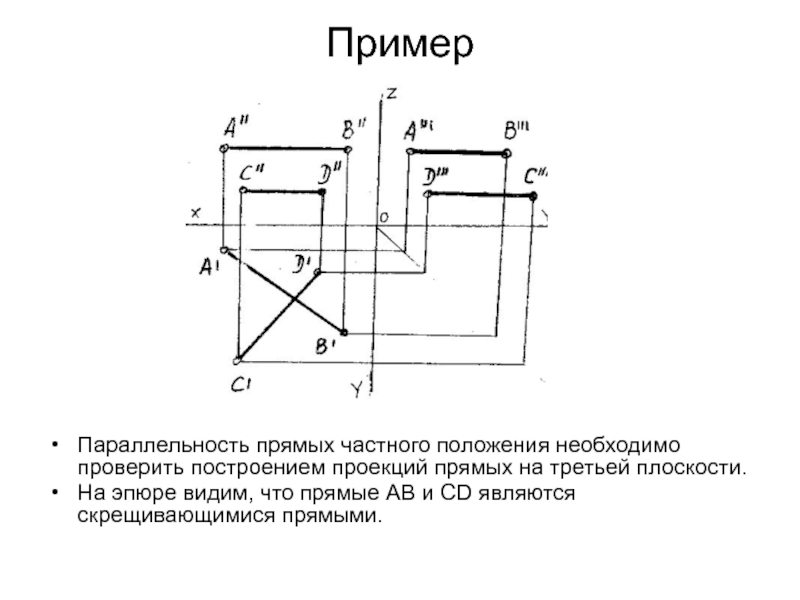
- 13. ПримерПараллельность прямых частного положения необходимо проверить построением
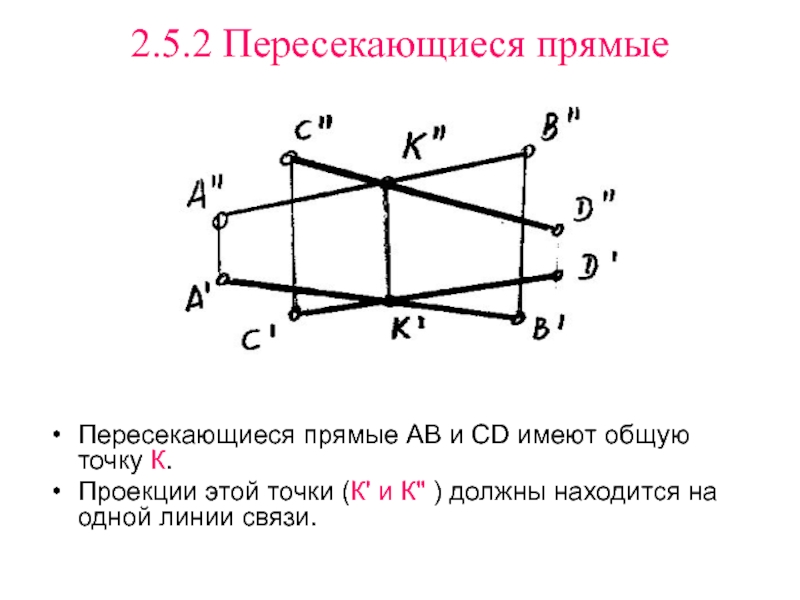
- 14. 2.5.2 Пересекающиеся прямыеПересекающиеся прямые АВ и СD
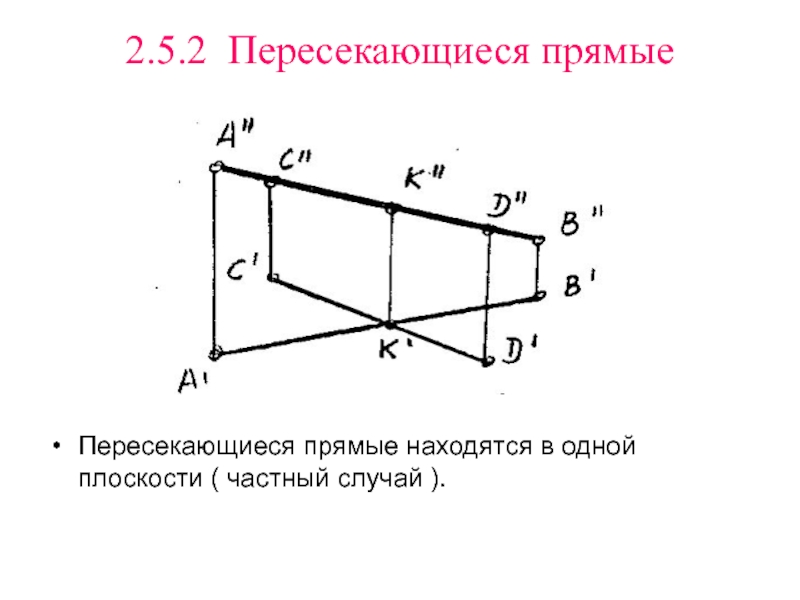
- 15. 2.5.2 Пересекающиеся прямые Пересекающиеся прямые находятся в одной плоскости ( частный случай ).
- 16. 2.5.2 Пересекающиеся прямые Пересекающиеся прямые, одна из
- 17. 2.5.4 Скрещивающиеся прямыеСкрещивающиеся прямые не имеют общих
- 18. 2.6 Проецирование прямого угла Условие: угол АВС=90°;
- 19. 2.6 Проецирование прямого углаЗадача: Построить проекции прямого
- 20. 2.6 Проецирование прямого углаЗадача: Построить проекции прямого
- 21. Спасибо за внимание
- 22. Инженерная и компьютерная графикаРаздел: начертательная геометрия
- 23. 3. Проецирование плоскости 3.1 Способы задания
- 24. 3.1 Способы задания плоскостиДвумя пересекающимися прямыми
- 25. 3.2 Проецирование плоскости общего положения
- 26. 3.2 Плоскость общего положенияЭпюр плоскости общего положения
- 27. 3.2 Плоскость общего положенияЭпюр плоскости общего положения
- 28. 3.3.1 Плоскости частного положения Проецирующая плоскостьАВС- плоскость горизонтально-проецирующаяПлоскость АВС перпендикулярна к плоскости проекций П1.
- 29. 3.3.1 Плоскости частного положения Проецирующая плоскостьАВС- плоскость фронтально –проецирующаяПлоскость АВС перпендикулярна к плоскости проекций П2.
- 30. АВС
- 31. 3.3.2 Плоскости частного положения Плоскость уровняАВСD- горизонтальная
- 32. 3.3.2 Плоскости частного положения Плоскость уровняАВСDEF- фронтальная
- 33. 3.3.2 Плоскости частного положения Плоскость уровняАВС- профильная
- 34. 3.4.Прямая и точка в плоскости1.Прямая принадлежит плоскости,
- 35. 3.4 Принадлежность прямой плоскостиПервое условие: Прямая АD
- 36. 3.4 Принадлежность прямой плоскостиВторое условие: Прямая DE
- 37. 3.4 Принадлежность точки плоскостиТочка К принадлежит плоскости
- 38. 3.4 Принадлежность прямой проецирующей плоскостигоризонтально- проецирующая
- 39. 3.5 Главные линии плоскостиАD- горизонталь плоскости; АЕ- фронталь плоскости; ВF-профильная прямая плоскости
- 40. 3.5 Главные линии плоскостиПример: EF-горизонталь плоскости, заданной двумя параллельными прямыми (АВ и СD).
- 41. 3.6 Проекции плоских фигурПроекции трапецииА'В' параллельна С'D' и А"В" параллельна C"D"
- 42. 3.7 Проекции плоских фигурПроекции пятиугольника АВСDE.Проекции точек пересечения диагоналей должны находиться на вертикальных линиях связи.
- 43. 3.8 Две параллельные плоскостиЕсли плоскости α и
- 44. 3.9 Пересечение прямой линии общего положения и плоскости общего положения
- 45. 3.9 Пересечение прямой линии общего положения с
- 46. 3.9 Пересечение прямой линии с горизонтальной плоскостьюК-
- 47. 3.9 Пересечение прямой общего положения и плоскости
- 48. 3.10 Прямая параллельная плоскостиПрямая параллельна плоскости, если
- 49. 3.11 Две параллельные плоскости Плоскости параллельны, если
- 50. 4. Методы преобразования чертежа 4.1 Метод перемены
- 51. 4.1 Метод перемены плоскостей проекцийОпределение проекций точки
- 52. 4.1 Метод перемены плоскостей проекций Преобразование прямой
- 53. 4.1 Метод перемены плоскостей проекцийПреобразование прямой уровня
- 54. 4.1 Метод перемены плоскостей проекцийПреобразование плоскости общего
- 55. 4.1 Метод перемены плоскостей проекцийПреобразование проецирующей плоскости
- 56. 4.1 Метод перемены плоскостей проекцийОпределение расстояния от
- 57. 4.1 Метод перемены плоскостей проекцийОпределить расстояние от
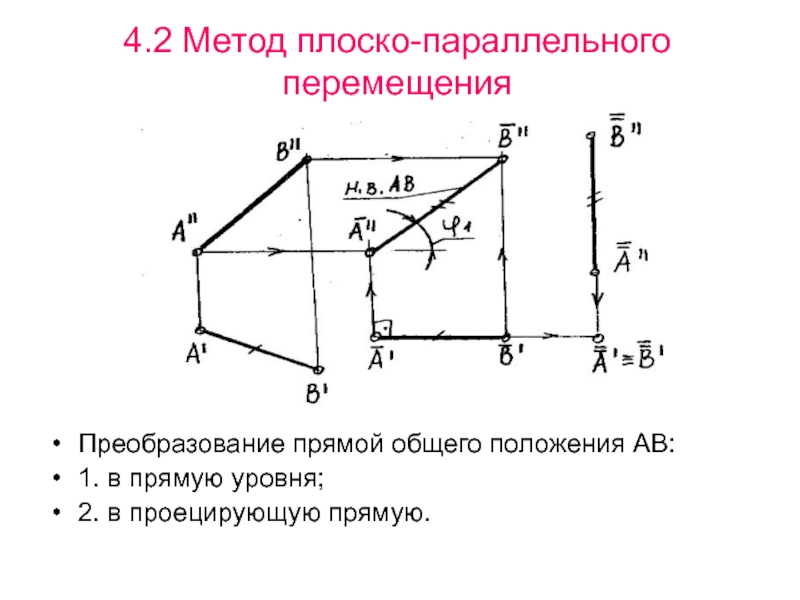
- 58. 4.2 Метод плоско-параллельного перемещения
- 59. 4.2 Метод плоско-параллельного перемещенияПреобразование прямой общего положения АВ:1. в прямую уровня;2. в проецирующую прямую.
- 60. Скачать презентанцию
Литература 1.В.М. Дегтярев, В.П. Затыльникова. Инженерная и компьютерная графика. М. Издательский центр 2010 2. В. О. Гордон, М. А. Семенцов-Огиевский. Курс начертательной геометрии. М. Наука, 1988.3. С. К. Боголюбов, Черчение. Машиностроение4.
Слайды и текст этой презентации
Слайд 2Литература
1.В.М. Дегтярев, В.П. Затыльникова. Инженерная и компьютерная графика. М.
Издательский центр 2010
2. В. О. Гордон, М. А.
Семенцов-Огиевский. Курс начертательной геометрии. М. Наука, 1988.3. С. К. Боголюбов, Черчение. Машиностроение
4. Методические указания к выполнению домашних заданий: задание №1,задание <Чертежи деталей>, задание:< Чтение и деталирование чертежа сборочной единицы>. < Электрические схемы (2008)> Издание ГУТ.
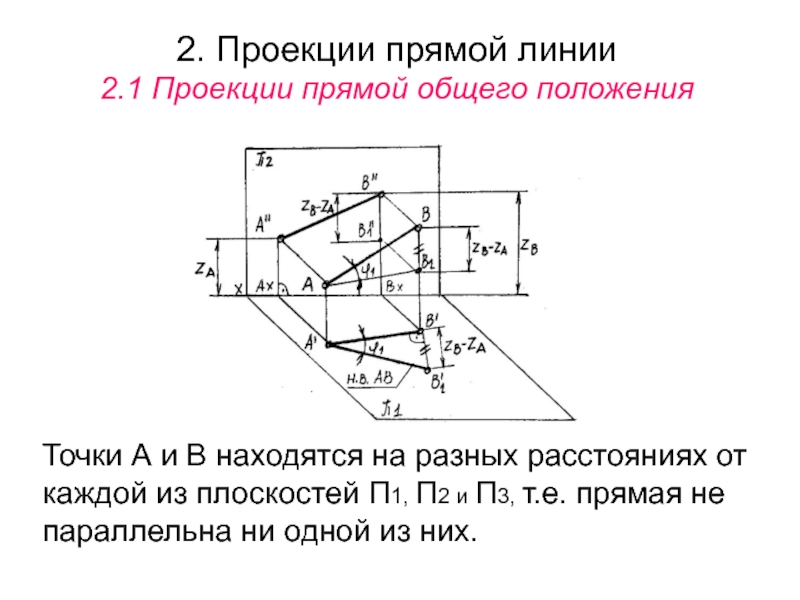
Слайд 42. Проекции прямой линии
2.1 Проекции прямой общего положения
Точки А и
В находятся на разных расстояниях от каждой из плоскостей П1,
П2 и П3, т.е. прямая не параллельна ни одной из них.
Слайд 52.1 Проекции прямой общего положения
(продолжение)
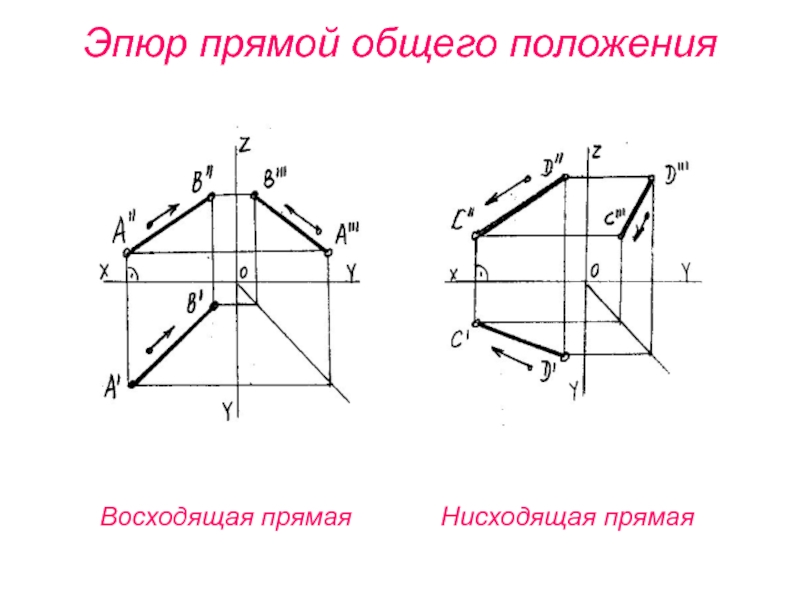
1. Прямая общего положения (О.П.)- эта
прямая непараллельная ни одной из плоскостей проекций;
2. Проекция прямой линии
общего положения всегда прямая линия; 3. Спроецировать прямую линию это значит спроецировать две её точки;
4. При прямоугольном проецировании проекция отрезка всегда меньше самого отрезка: IА'В'I = IАВ1I = IАВI· cos φ1, т.е.
I А'В'I < IАВ I ; IА"В"I < IАВI ; IА'"В'" I < I АВI
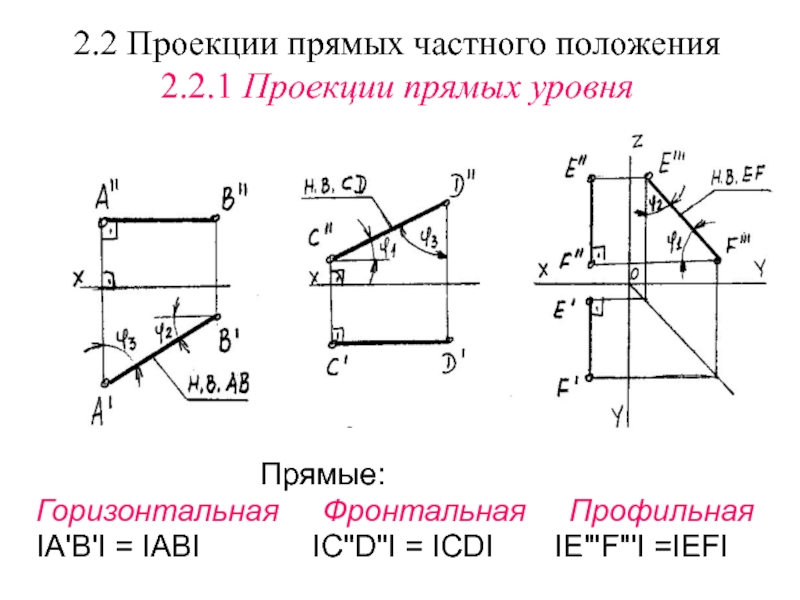
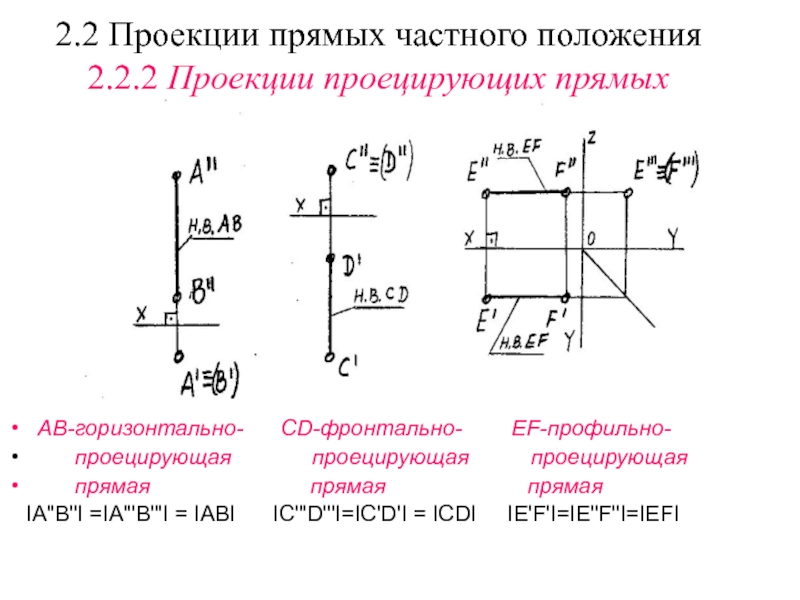
Слайд 72.2 Проекции прямых частного положения
2.2.1 Проекции прямых уровня
Прямые:
Горизонтальная Фронтальная Профильная
IА'В'I = IАВI IС"D"I = IСDI IЕ"'F"'I =IEFI
Слайд 82.2 Проекции прямых частного положения
2.2.2 Проекции проецирующих прямых
АВ-горизонтально-
СD-фронтально- ЕF-профильно-
проецирующая
проецирующая проецирующаяпрямая прямая прямая
IА"В"I =IА"'В"'I = IАВI IС"'D"'I=IC'D'I = ICDI IЕ'F'I=IE"F"I=IEFI
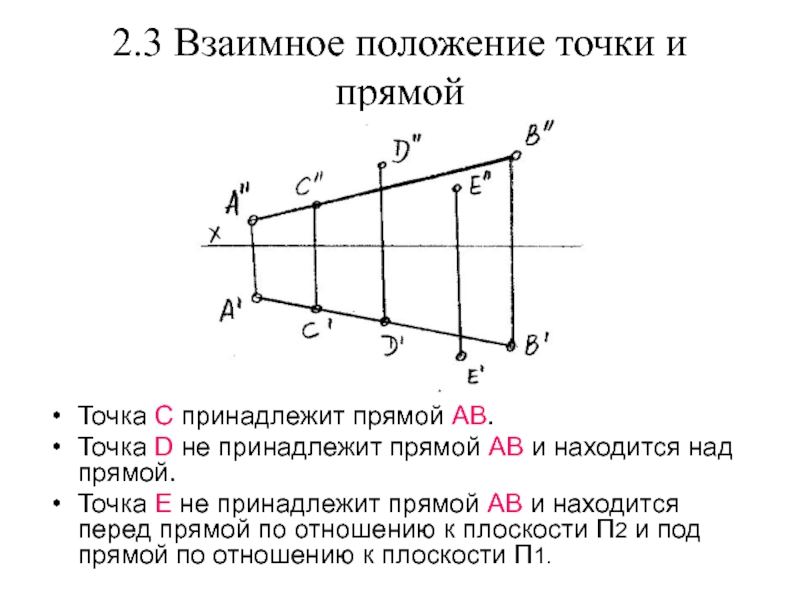
Слайд 92.3 Взаимное положение точки и прямой
Точка С принадлежит прямой АВ.
Точка D не принадлежит прямой АВ и находится над прямой.
Точка Е не принадлежит прямой АВ и находится перед прямой по отношению к плоскости П2 и под прямой по отношению к плоскости П1.
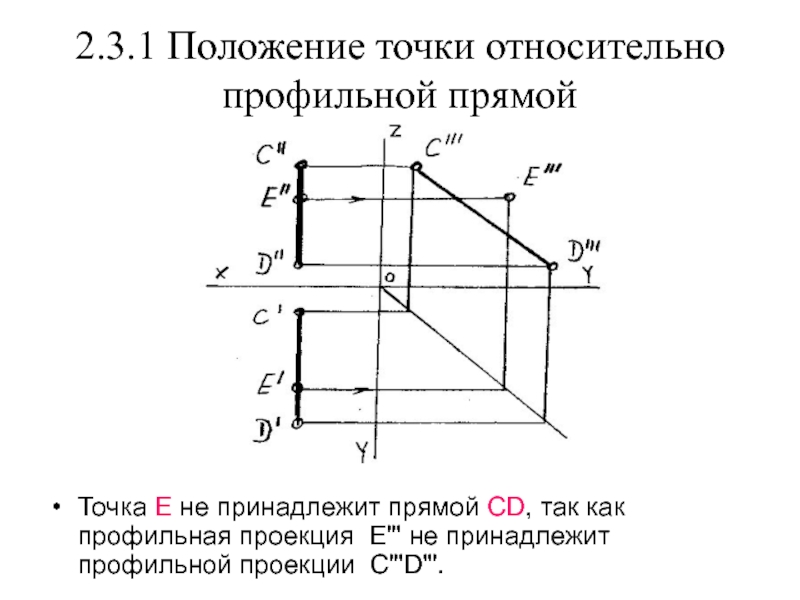
Слайд 102.3.1 Положение точки относительно профильной прямой
Точка Е не принадлежит прямой
СD, так как профильная проекция Е"' не принадлежит профильной проекции
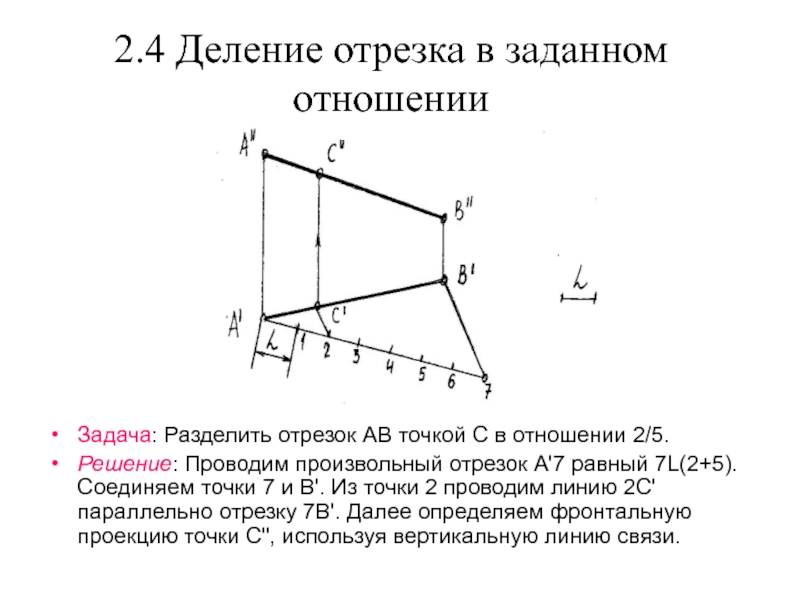
С"'D"'.
Слайд 112.4 Деление отрезка в заданном отношении
Задача: Разделить отрезок АВ точкой
С в отношении 2/5.
Решение: Проводим произвольный отрезок А'7 равный
7L(2+5). Соединяем точки 7 и В'. Из точки 2 проводим линию 2С' параллельно отрезку 7В'. Далее определяем фронтальную проекцию точки С", используя вертикальную линию связи. 
Слайд 122.5.1 Параллельные прямые
Прямые АВ и СD параллельны между собой, так
как одноименные проекции прямых параллельны между собой( А'В' II С'D'
и А"В"II С"D" ).Это условие справедливо только для прямых общего положения.
Слайд 13Пример
Параллельность прямых частного положения необходимо проверить построением проекций прямых на
третьей плоскости.
На эпюре видим, что прямые АВ и СD являются
скрещивающимися прямыми.
Слайд 142.5.2 Пересекающиеся прямые
Пересекающиеся прямые АВ и СD имеют общую точку
К.
Проекции этой точки (К' и К" ) должны находится на
одной линии связи. 
Слайд 15
2.5.2 Пересекающиеся прямые
Пересекающиеся прямые находятся в одной плоскости ( частный
случай ).
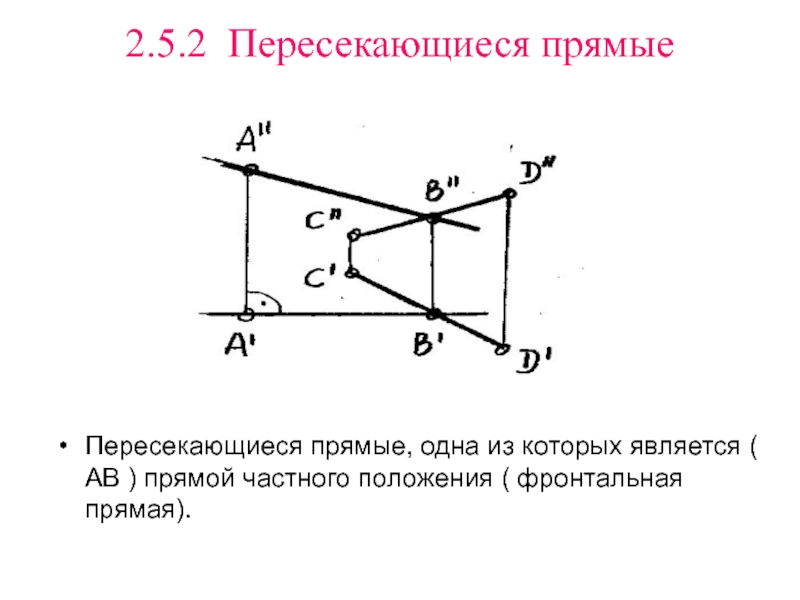
Слайд 162.5.2 Пересекающиеся прямые
Пересекающиеся прямые, одна из которых является (
АВ ) прямой частного положения ( фронтальная прямая).
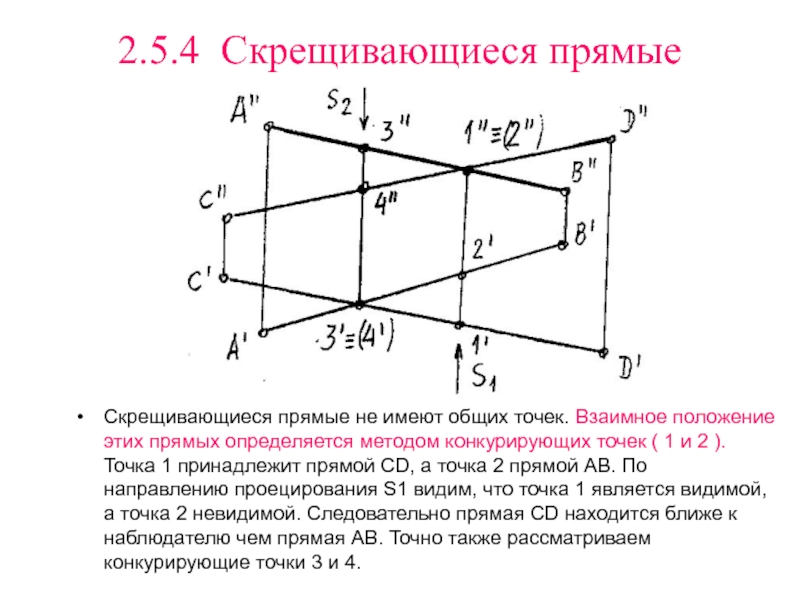
Слайд 172.5.4 Скрещивающиеся прямые
Скрещивающиеся прямые не имеют общих точек. Взаимное положение
этих прямых определяется методом конкурирующих точек ( 1 и 2
). Точка 1 принадлежит прямой СD, а точка 2 прямой АВ. По направлению проецирования S1 видим, что точка 1 является видимой, а точка 2 невидимой. Следовательно прямая СD находится ближе к наблюдателю чем прямая АВ. Точно также рассматриваем конкурирующие точки 3 и 4.
Слайд 182.6 Проецирование прямого угла
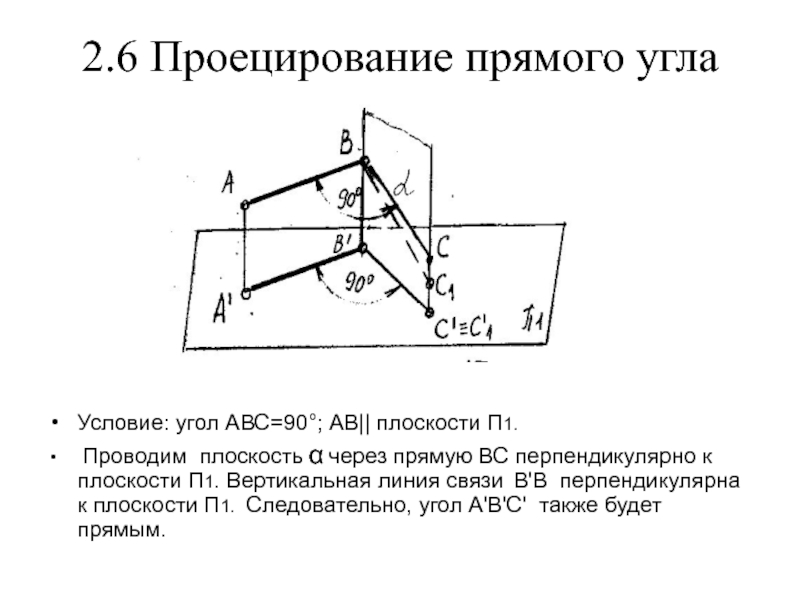
Условие: угол АВС=90°; АВ|| плоскости П1.
Проводим плоскость α через прямую ВС перпендикулярно к плоскости П1.
Вертикальная линия связи В'В перпендикулярна к плоскости П1. Следовательно, угол А'В'С' также будет прямым.
Слайд 192.6 Проецирование прямого угла
Задача: Построить проекции прямого угла между прямыми
АВ и ВС при условии, что прямая АВ II плоскости
П1.Если проекция некоторого угла, у которого одна сторона параллельна плоскости проекций, представляет собой прямой угол, то проецируемый угол тоже прямой. На плоскости П1 угол между А'В' и В'С' должен быть построен в виде прямого угла.
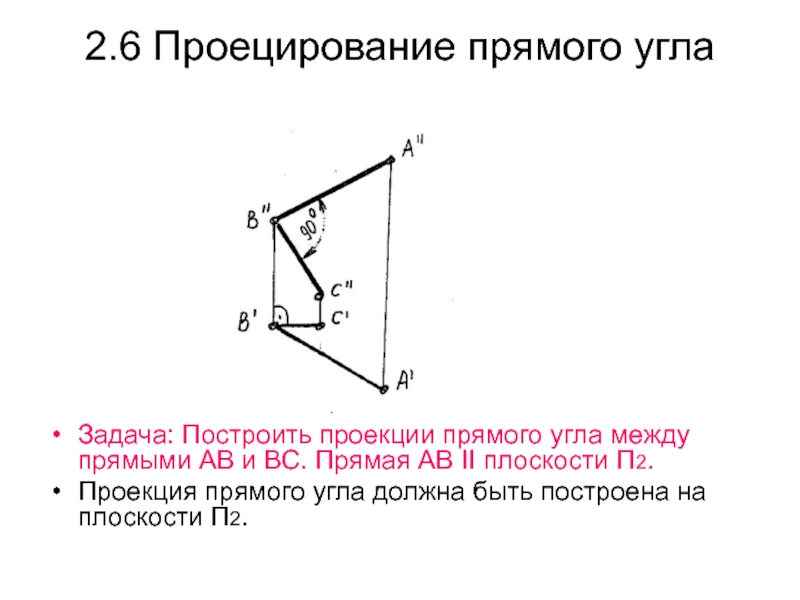
Слайд 202.6 Проецирование прямого угла
Задача: Построить проекции прямого угла между прямыми
АВ и ВС. Прямая АВ II плоскости П2.
Проекция прямого угла
должна быть построена на плоскости П2.
Слайд 22Инженерная и компьютерная графика
Раздел: начертательная геометрия
Лекция № 3
Проецирование плоскости
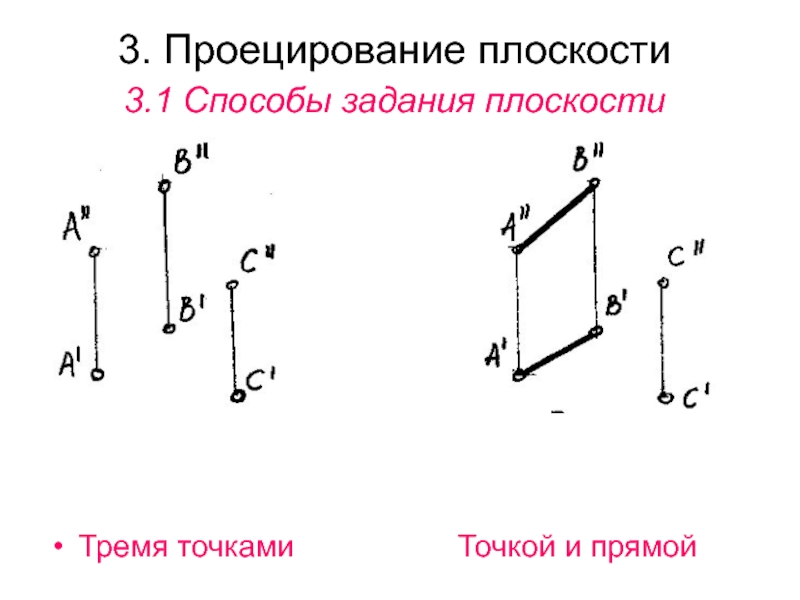
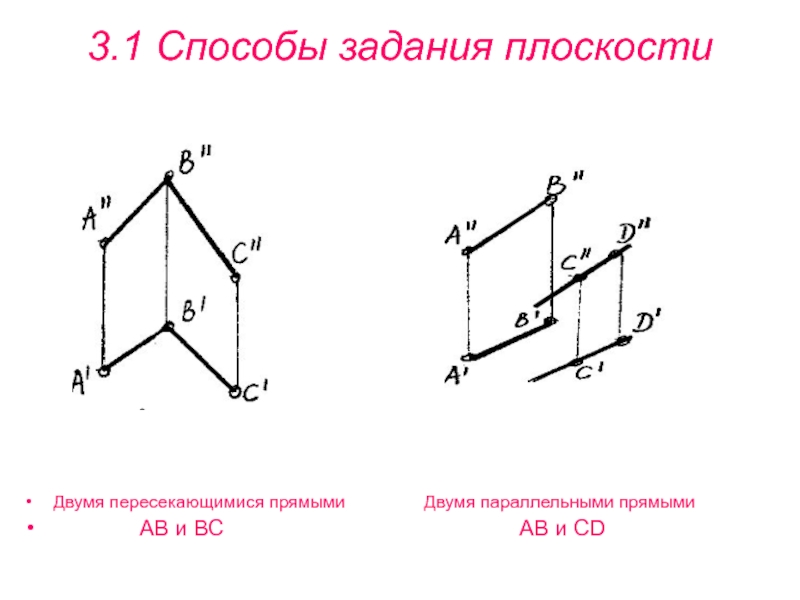
Слайд 243.1 Способы задания плоскости
Двумя пересекающимися прямыми
Двумя параллельными прямыми
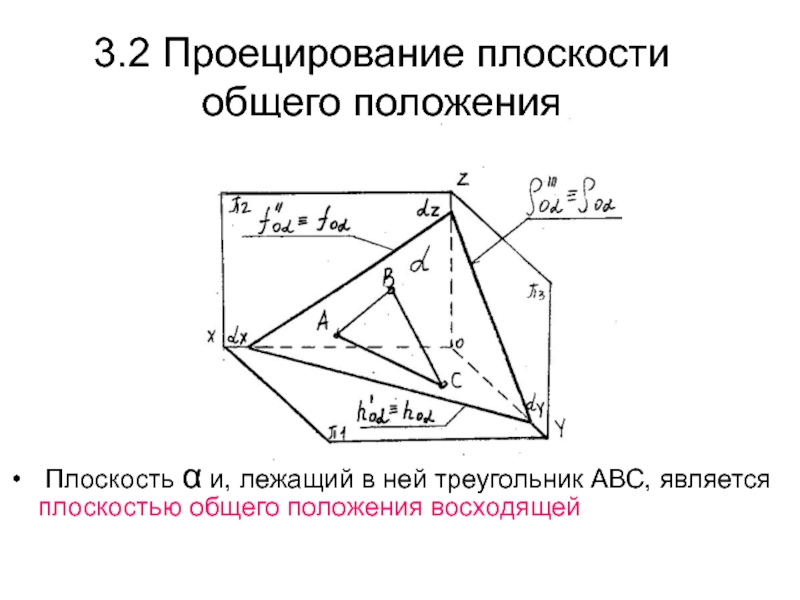
АВ и ВС АВ и СD
Слайд 253.2 Проецирование плоскости общего положения
Плоскость α и,
лежащий в ней треугольник АВС, является плоскостью общего положения восходящей
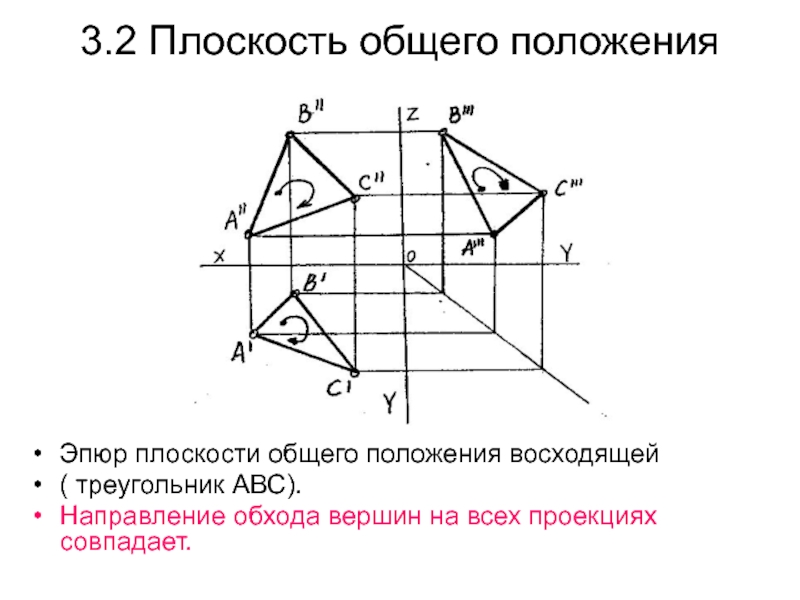
Слайд 263.2 Плоскость общего положения
Эпюр плоскости общего положения восходящей
( треугольник
АВС).
Направление обхода вершин на всех проекциях совпадает.
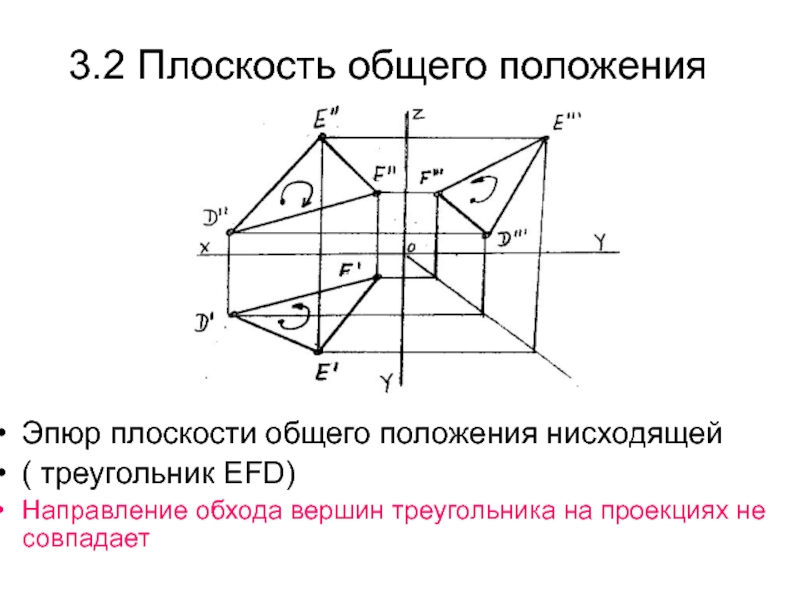
Слайд 273.2 Плоскость общего положения
Эпюр плоскости общего положения нисходящей
( треугольник EFD)
Направление
обхода вершин треугольника на проекциях не совпадает
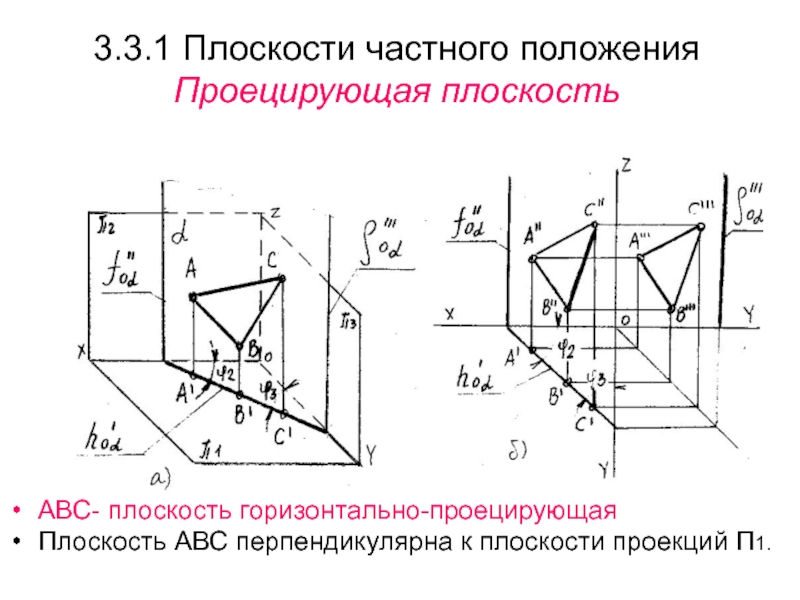
Слайд 283.3.1 Плоскости частного положения
Проецирующая плоскость
АВС- плоскость горизонтально-проецирующая
Плоскость АВС перпендикулярна к
плоскости проекций П1.
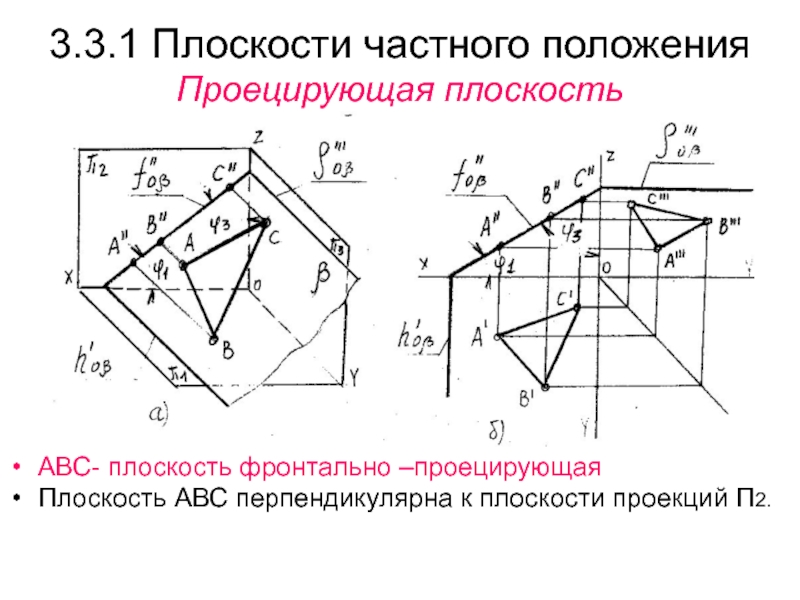
Слайд 293.3.1 Плоскости частного положения
Проецирующая плоскость
АВС- плоскость фронтально –проецирующая
Плоскость АВС
перпендикулярна к плоскости проекций П2.
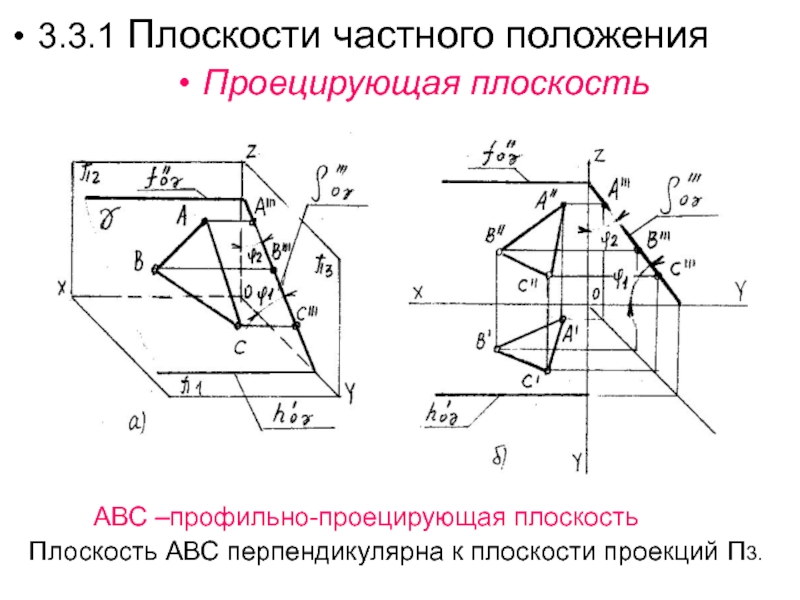
Слайд 30 АВС –профильно-проецирующая плоскость
Плоскость АВС перпендикулярна к плоскости проекций П3.
3.3.1 Плоскости частного
положенияПроецирующая плоскость
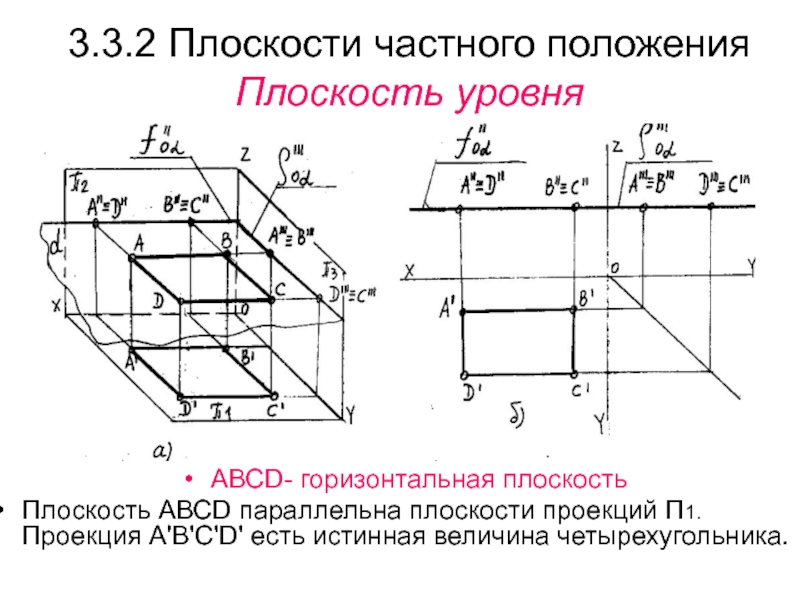
Слайд 313.3.2 Плоскости частного положения
Плоскость уровня
АВСD- горизонтальная плоскость
Плоскость АВСD параллельна плоскости
проекций П1. Проекция А'В'С'D' есть истинная величина четырехугольника.
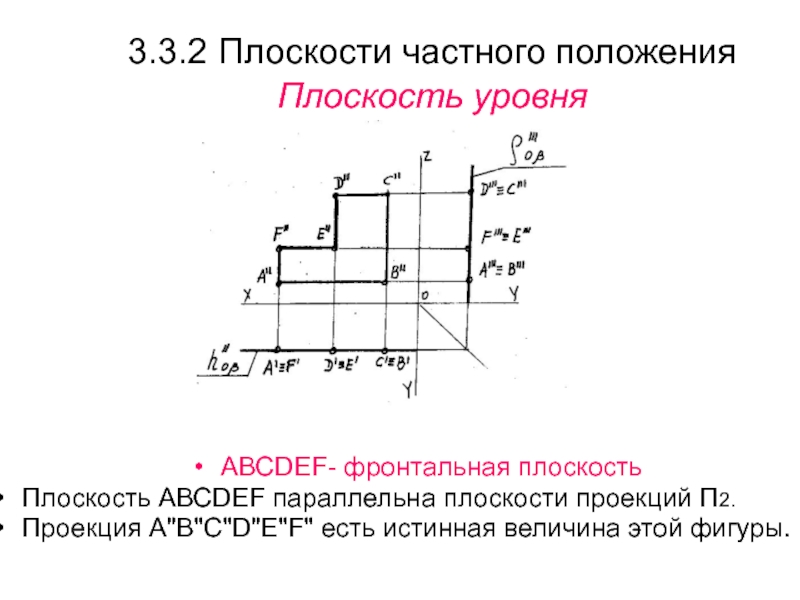
Слайд 323.3.2 Плоскости частного положения
Плоскость уровня
АВСDEF- фронтальная плоскость
Плоскость АВСDEF параллельна плоскости
проекций П2.
Проекция А"В"С"D"E"F" есть истинная величина этой фигуры.
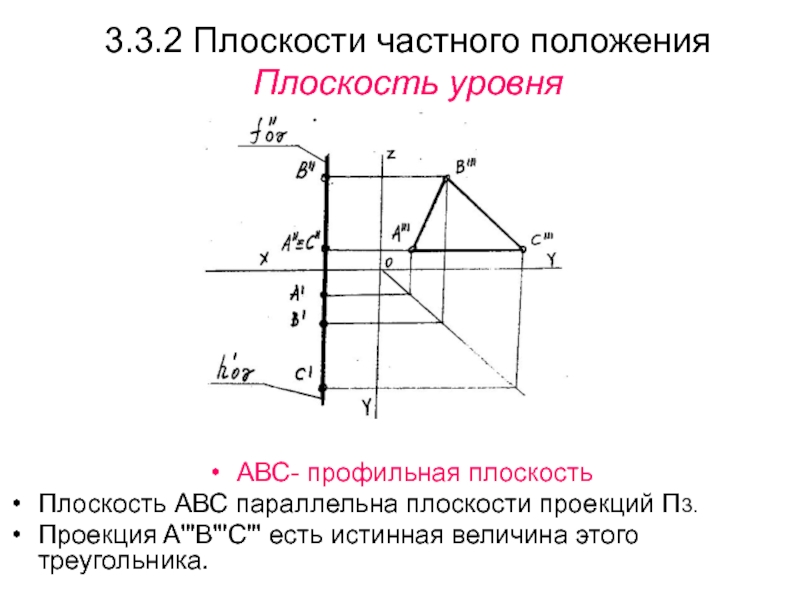
Слайд 333.3.2 Плоскости частного положения
Плоскость уровня
АВС- профильная плоскость
Плоскость АВС параллельна плоскости
проекций П3.
Проекция А'"В"'С"' есть истинная величина этого треугольника.
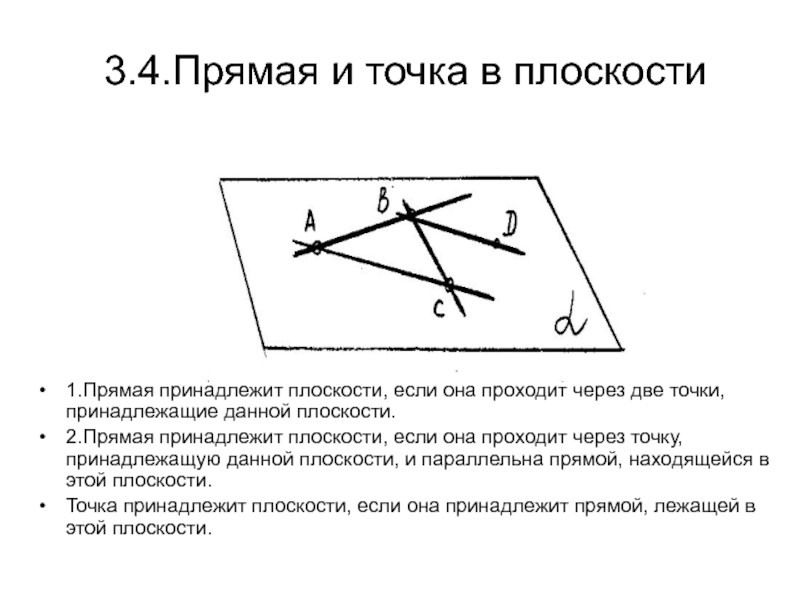
Слайд 343.4.Прямая и точка в плоскости
1.Прямая принадлежит плоскости, если она проходит
через две точки, принадлежащие данной плоскости.
2.Прямая принадлежит плоскости, если она
проходит через точку, принадлежащую данной плоскости, и параллельна прямой, находящейся в этой плоскости.Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
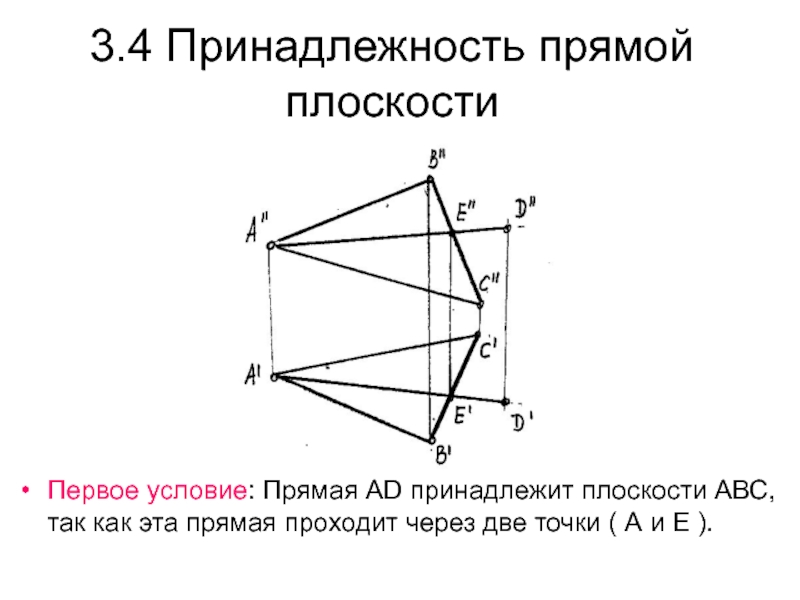
Слайд 353.4 Принадлежность прямой плоскости
Первое условие: Прямая АD принадлежит плоскости АВС,
так как эта прямая проходит через две точки ( А
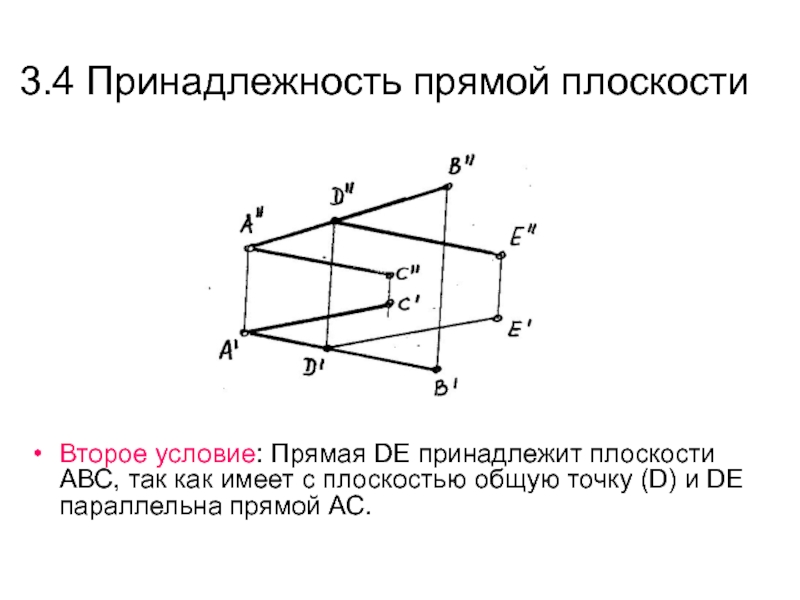
и Е ).
Слайд 363.4 Принадлежность прямой плоскости
Второе условие: Прямая DE принадлежит плоскости АВС,
так как имеет с плоскостью общую точку (D) и DE
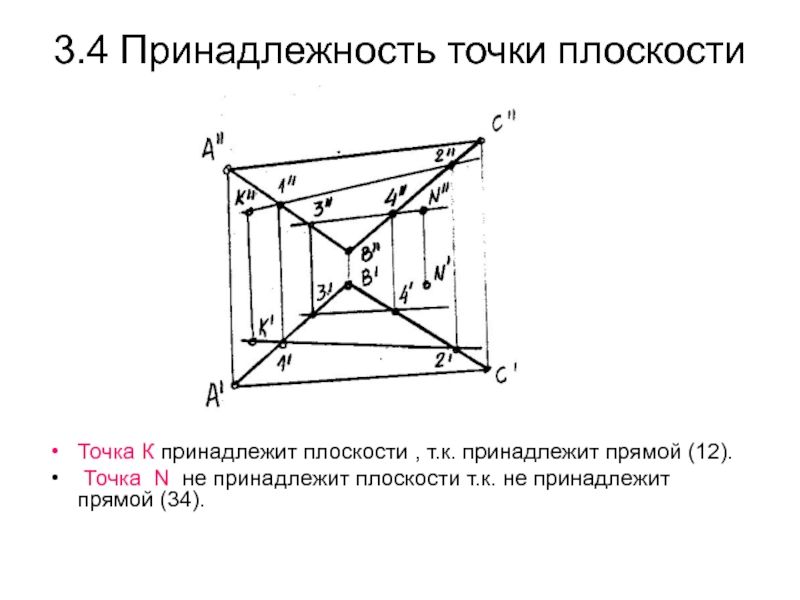
параллельна прямой АС.
Слайд 373.4 Принадлежность точки плоскости
Точка К принадлежит плоскости , т.к. принадлежит
прямой (12).
Точка N не принадлежит плоскости т.к. не принадлежит
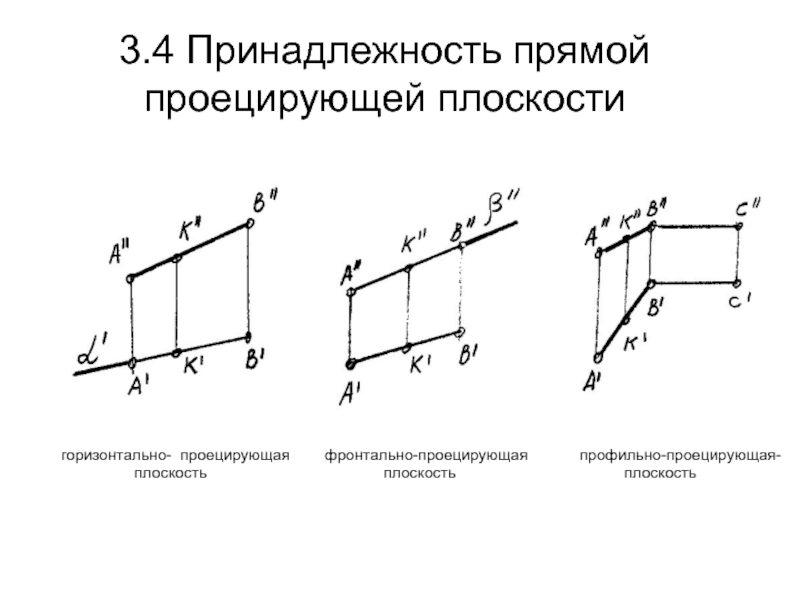
прямой (34).
Слайд 383.4 Принадлежность прямой проецирующей плоскости
горизонтально- проецирующая фронтально-проецирующая
профильно-проецирующая-
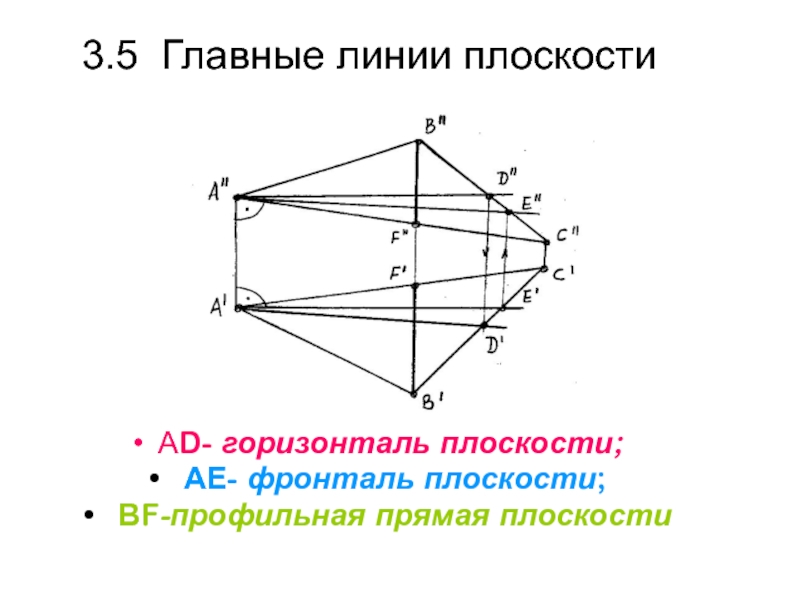
плоскость плоскость плоскость
Слайд 393.5 Главные линии плоскости
АD- горизонталь плоскости;
АЕ- фронталь плоскости;
ВF-профильная
прямая плоскости
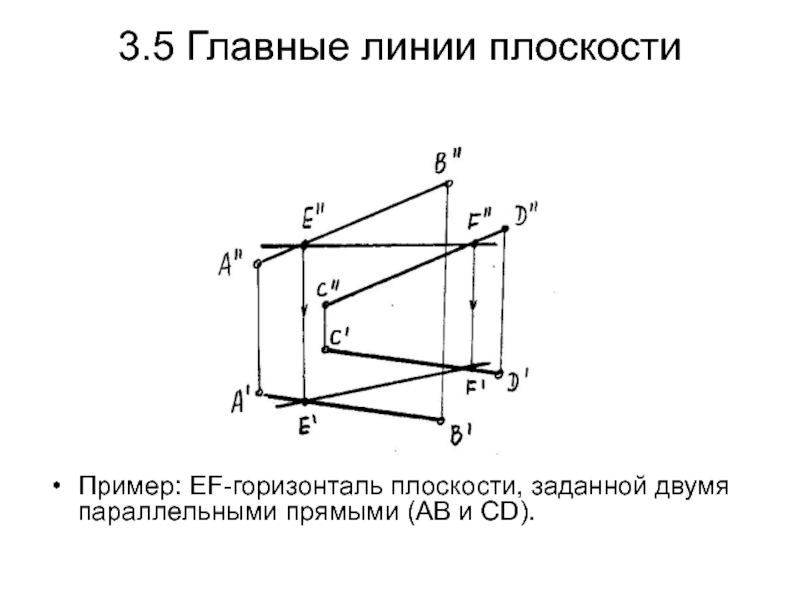
Слайд 403.5 Главные линии плоскости
Пример: EF-горизонталь плоскости, заданной двумя параллельными прямыми
(АВ и СD).
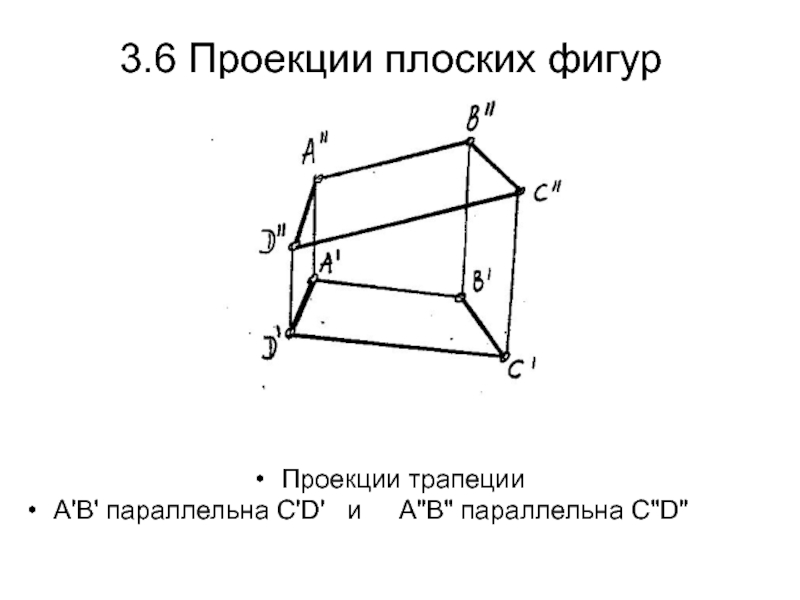
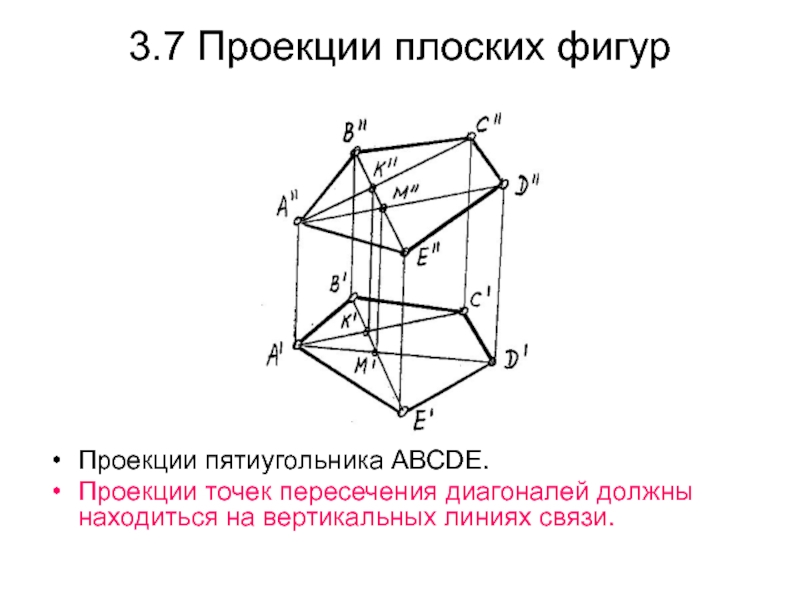
Слайд 423.7 Проекции плоских фигур
Проекции пятиугольника АВСDE.
Проекции точек пересечения диагоналей должны
находиться на вертикальных линиях связи.
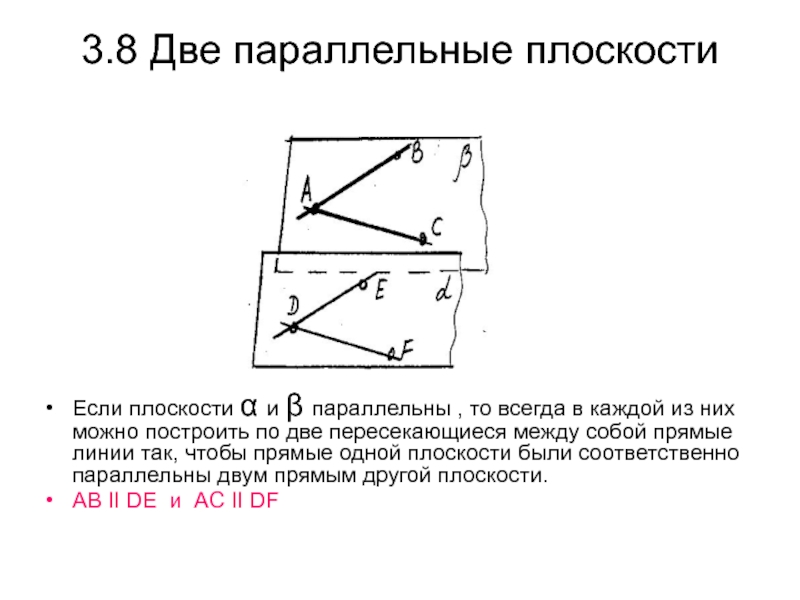
Слайд 433.8 Две параллельные плоскости
Если плоскости α и β параллельны ,
то всегда в каждой из них можно построить по две
пересекающиеся между собой прямые линии так, чтобы прямые одной плоскости были соответственно параллельны двум прямым другой плоскости.АВ II DE и AC II DF
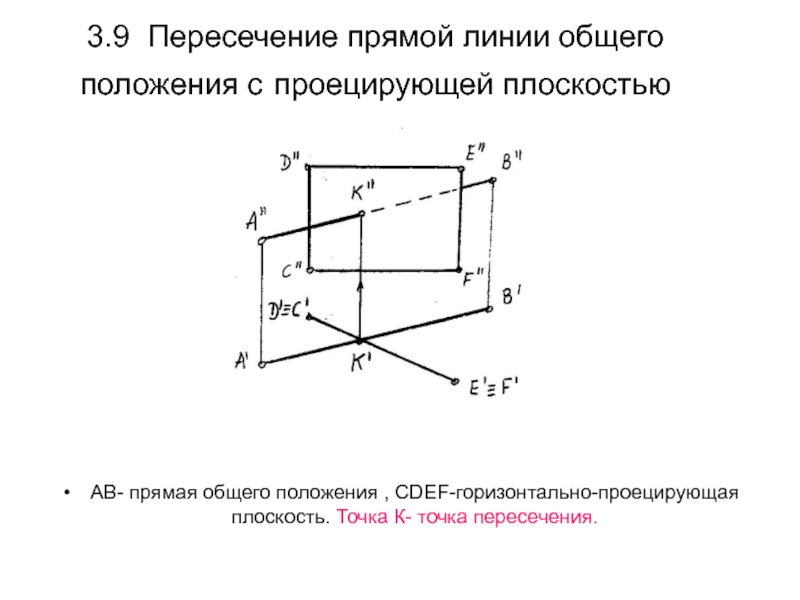
Слайд 453.9 Пересечение прямой линии общего положения с проецирующей плоскостью
АВ- прямая
общего положения , CDEF-горизонтально-проецирующая плоскость. Точка К- точка пересечения.
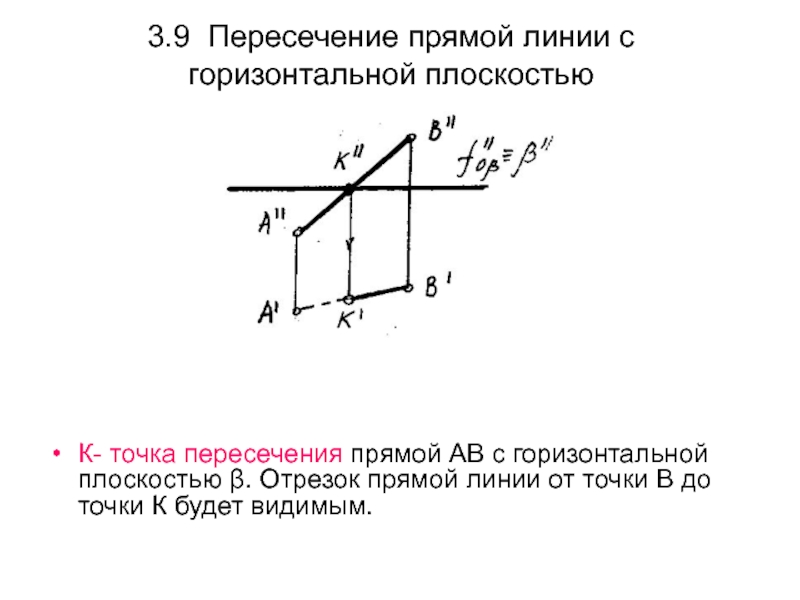
Слайд 463.9 Пересечение прямой линии с горизонтальной плоскостью
К- точка пересечения прямой
АВ с горизонтальной плоскостью β. Отрезок прямой линии от точки
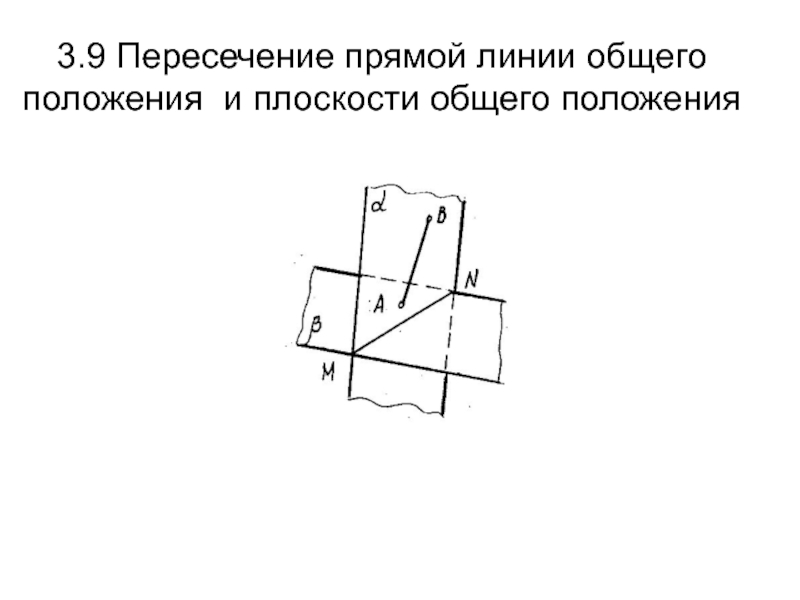
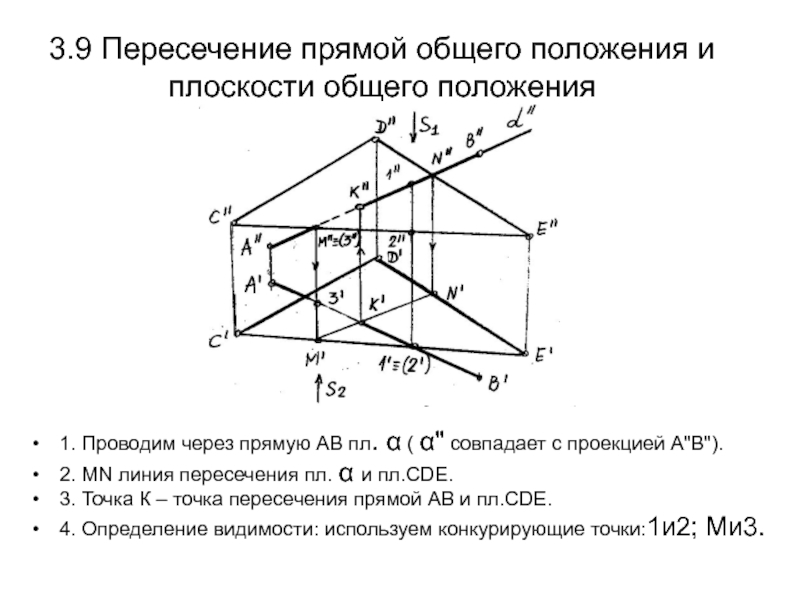
В до точки К будет видимым.
Слайд 473.9 Пересечение прямой общего положения и плоскости общего положения
1. Проводим
через прямую АВ пл. α ( α" совпадает с проекцией
А"В").2. МN линия пересечения пл. α и пл.СDE.
3. Точка К – точка пересечения прямой АВ и пл.СDE.
4. Определение видимости: используем конкурирующие точки:1и2; Ми3.
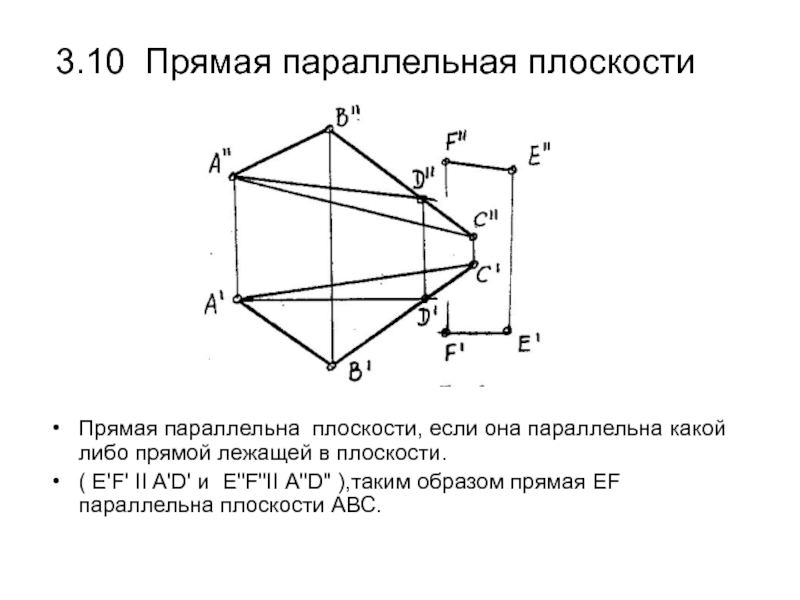
Слайд 483.10 Прямая параллельная плоскости
Прямая параллельна плоскости, если она параллельна какой
либо прямой лежащей в плоскости.
( E'F' II A'D' и E"F"II
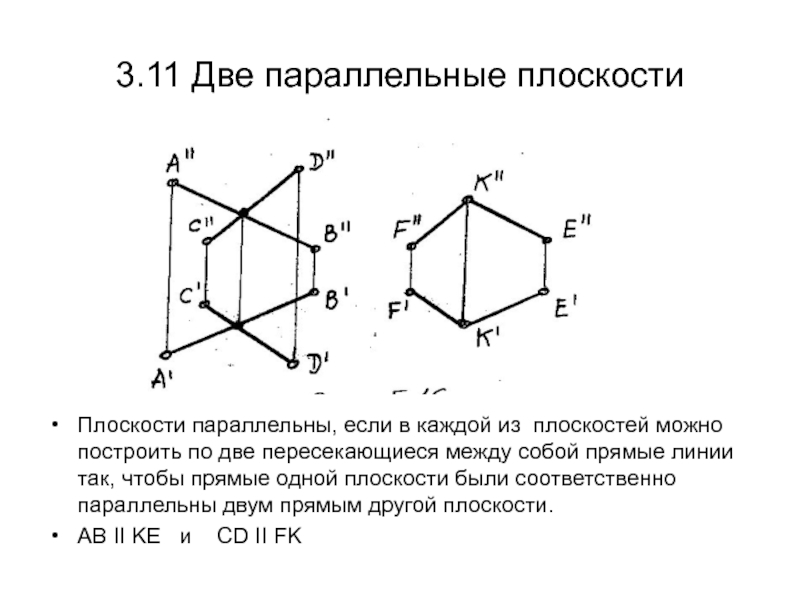
А"D" ),таким образом прямая EF параллельна плоскости АВС.
Слайд 493.11 Две параллельные плоскости
Плоскости параллельны, если в каждой из
плоскостей можно построить по две пересекающиеся между собой прямые линии
так, чтобы прямые одной плоскости были соответственно параллельны двум прямым другой плоскости.АВ II KE и CD II FK
Слайд 504. Методы преобразования чертежа
4.1 Метод перемены плоскостей проекций
Исходная система плоскостей
[П1/П2]. Проекции точки А: А' и А"
Переходим к новой системе плоскостей [П1/П3]. Плоскость П3 перпендикулярна к плоскости П1. Проекции точки А: А' и А"'
Координата ZА для точки А сохраняет своё значение.
Линия связи А'А" перпендикулярна к оси [П1/П2].
Линия связи А'А'" перпендикулярна к оси [П1/П3].
![4. Методы преобразования чертежа 4.1 Метод перемены плоскостей проекцийИсходная система плоскостей [П1/П2]. Проекции точки А: А' и](/img/thumbs/1c1000627375349369a9eefe07439ae2-800x.jpg "Инженерная и компьютерная графика 4. Методы преобразования чертежа 4.1 Метод перемены плоскостей проекцийИсходная система плоскостей")
Слайд 514.1 Метод перемены плоскостей проекций
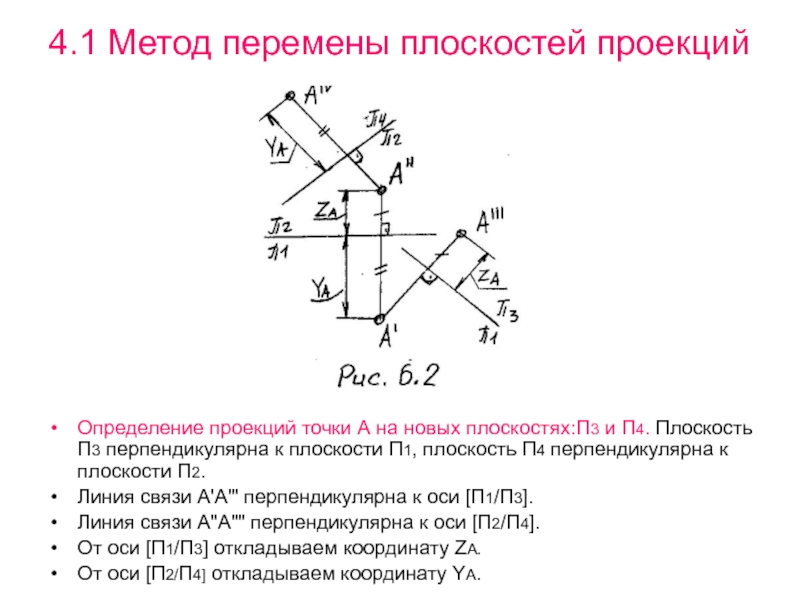
Определение проекций точки А на новых
плоскостях:П3 и П4. Плоскость П3 перпендикулярна к плоскости П1, плоскость
П4 перпендикулярна к плоскости П2.Линия связи А'А"' перпендикулярна к оси [П1/П3].
Линия связи А"А"" перпендикулярна к оси [П2/П4].
От оси [П1/П3] откладываем координату ZА.
От оси [П2/П4] откладываем координату YА.
Слайд 524.1 Метод перемены плоскостей проекций
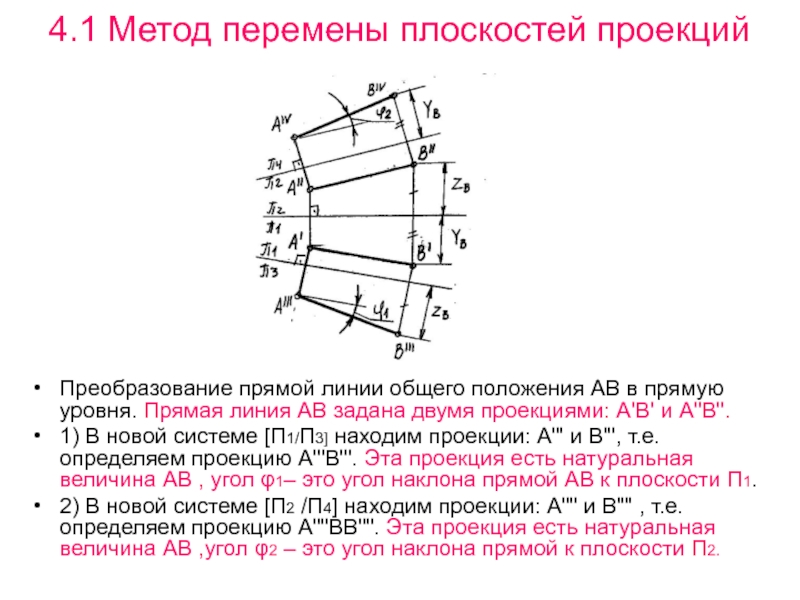
Преобразование прямой линии общего положения
АВ в прямую уровня. Прямая линия АВ задана двумя проекциями:
А'В' и А"В".1) В новой системе [П1/П3] находим проекции: А"' и В"', т.е. определяем проекцию А'"В'". Эта проекция есть натуральная величина АВ , угол φ1– это угол наклона прямой АВ к плоскости П1.
2) В новой системе [П2 /П4] находим проекции: А"" и В"" , т.е. определяем проекцию А""ВВ"". Эта проекция есть натуральная величина АВ ,угол φ2 – это угол наклона прямой к плоскости П2.
Слайд 534.1 Метод перемены плоскостей проекций
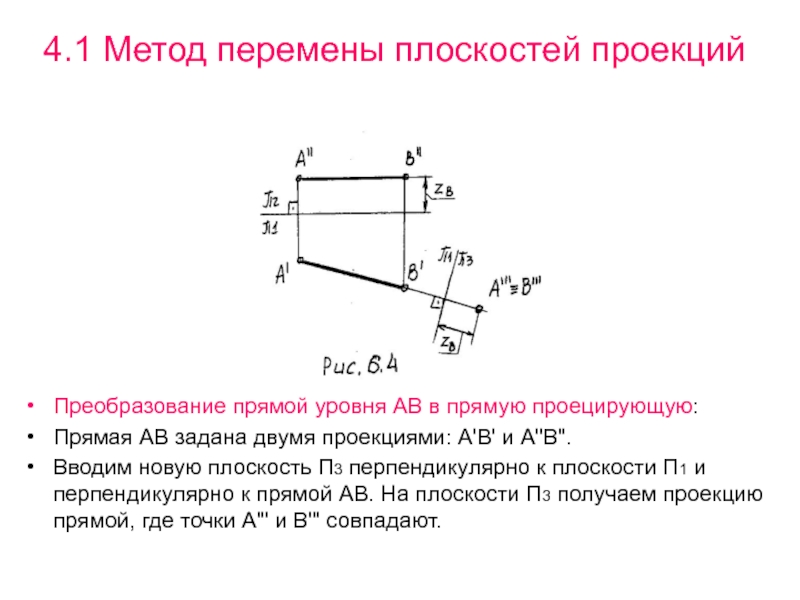
Преобразование прямой уровня АВ в прямую
проецирующую:
Прямая АВ задана двумя проекциями: А'В' и А"В".
Вводим новую плоскость
П3 перпендикулярно к плоскости П1 и перпендикулярно к прямой АВ. На плоскости П3 получаем проекцию прямой, где точки А"' и В"' совпадают.
Слайд 544.1 Метод перемены плоскостей проекций
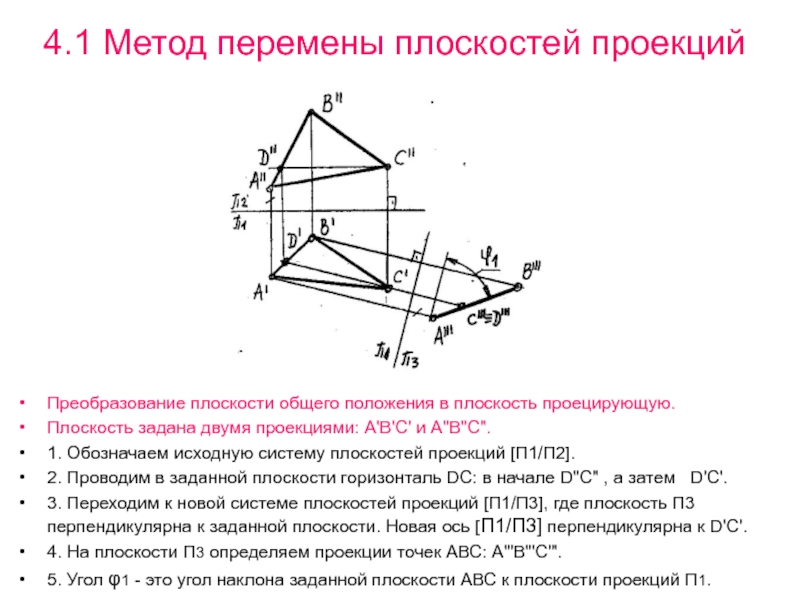
Преобразование плоскости общего положения в плоскость
проецирующую.
Плоскость задана двумя проекциями: А'В'С' и А"В"С".
1. Обозначаем исходную систему
плоскостей проекций [П1/П2].2. Проводим в заданной плоскости горизонталь DC: в начале D"C" , а затем D'C'.
3. Переходим к новой системе плоскостей проекций [П1/П3], где плоскость П3 перпендикулярна к заданной плоскости. Новая ось [П1/П3] перпендикулярна к D'C'.
4. На плоскости П3 определяем проекции точек АВС: А"'В"'С'".
5. Угол φ1 - это угол наклона заданной плоскости АВС к плоскости проекций П1.
Слайд 554.1 Метод перемены плоскостей проекций
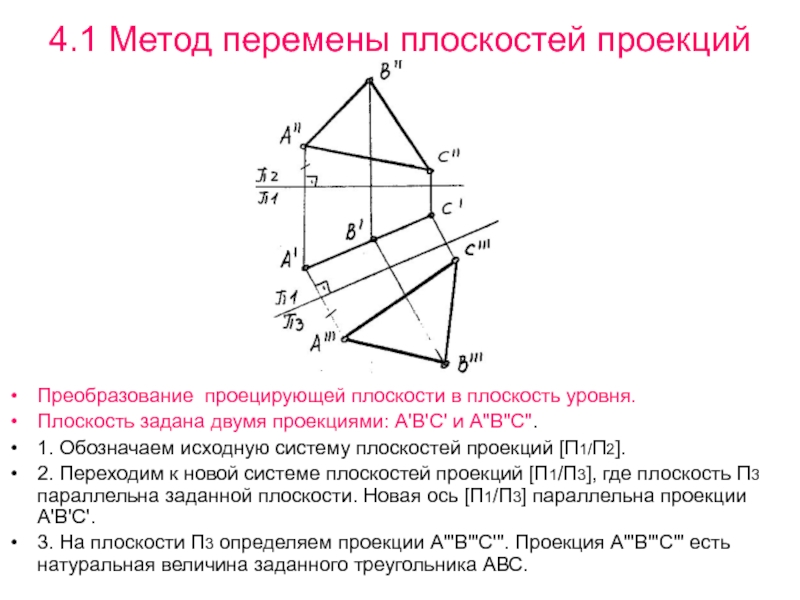
Преобразование проецирующей плоскости в плоскость уровня.
Плоскость
задана двумя проекциями: А'В'С' и А"В"С".
1. Обозначаем исходную систему плоскостей
проекций [П1/П2].2. Переходим к новой системе плоскостей проекций [П1/П3], где плоскость П3 параллельна заданной плоскости. Новая ось [П1/П3] параллельна проекции А'В'С'.
3. На плоскости П3 определяем проекции А"'В"'С'". Проекция А"'В"'С"' есть натуральная величина заданного треугольника АВС.
Слайд 564.1 Метод перемены плоскостей проекций
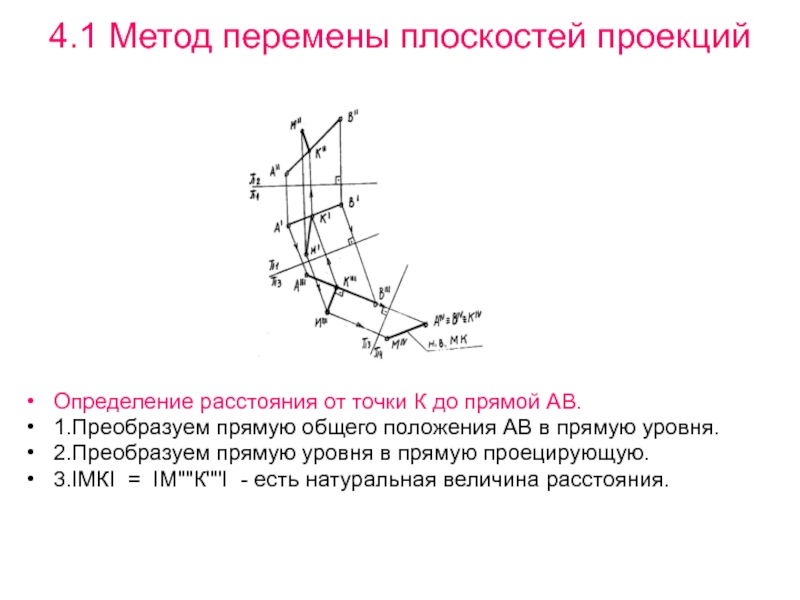
Определение расстояния от точки К до
прямой АВ.
1.Преобразуем прямую общего положения АВ в прямую уровня.
2.Преобразуем прямую
уровня в прямую проецирующую.3.IМКI = IМ""К""I - есть натуральная величина расстояния.
Слайд 574.1 Метод перемены плоскостей проекций
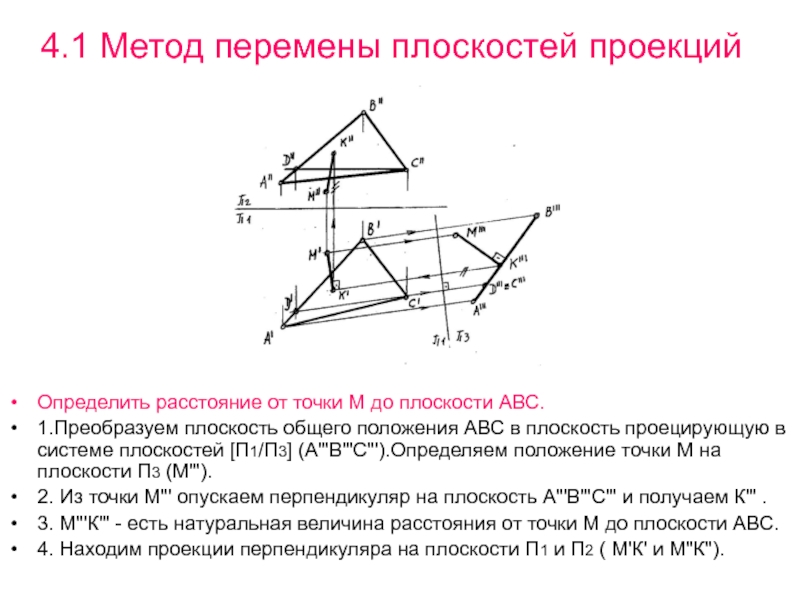
Определить расстояние от точки М до
плоскости АВС.
1.Преобразуем плоскость общего положения АВС в плоскость проецирующую в
системе плоскостей [П1/П3] (А"'В"'С"').Определяем положение точки М на плоскости П3 (М"').2. Из точки М"' опускаем перпендикуляр на плоскость А"'В"'С"' и получаем К"' .
3. М"'К"' - есть натуральная величина расстояния от точки М до плоскости АВС.
4. Находим проекции перпендикуляра на плоскости П1 и П2 ( М'К' и М"К").
Слайд 594.2 Метод плоско-параллельного перемещения
Преобразование прямой общего положения АВ:
1. в прямую
уровня;
2. в проецирующую прямую.
